不同水胶比自密实混凝土的强度及波速测试研究
2021-05-06李富民李晟文
杨 巧,李富民,李晟文,王 辉
(1. 江海职业技术学院 土木工程学院, 江苏 扬州 225100; 2. 中国矿业大学 力学与土木工程学院, 江苏 徐州 221116;3. 九州职业技术学院 土木工程系, 江苏 徐州 221116; 4. 扬州新扬建工程建设有限公司 合约部, 江苏 扬州 225100)
0 引 言
近年来,自密实混凝土因其独特优势而逐渐广泛应用于各类工程中。强度是混凝土性能评价的重要指标,已有研究指出自密实混凝土强度与其自身拌合物原材料有着密切的关系[1-6],得出其抗压强度与水胶比和龄期[7]、等效水胶比的函数关系[8]。上述研究主要针对强度的影响因素展开,而关于自密实混凝土强度与波速关系的研究较少。有学者对普通混凝土强度与波速关系进行了试验研究[9-11],得出了一些结论。自密实混凝土虽与普通混凝土拌合物采用的原材料相同,但其具有矿物添加比高(需添加高效减水剂)、砂率较大、骨料粒径小等特点[12],其内部细微结构与普通混凝土有明显区别。因此,能否用超声波无损检测自密实混凝土强度,还需要进一步验证。
针对上述问题,本文配制了水胶比分别为0.52、0.48、0.44、0.40 的自密实混凝土试件,在养护龄期 7、14、28、56、84、112 d 时分别进行波速与强度测试,探讨了自密实混凝土强度与波速随龄期变化的规律,分析了一定龄期内不同水胶比自密实混凝土的强度与波速的关系,且进行曲线模拟,以期为发展适应本地区工程实际的自密实混凝土强度无破损检测技术提供参考。
1 试验材料及方法
1.1 材料
水泥为扬州产亚东牌 P·O 42.5 级,密度3 000 kg/m3,烧失量 4.88 %,初凝 200 min,终凝255 min,3 d、28 d 抗折强度 5.5 MPa、8.2 MPa,3 d、28 d 抗压强度为 27.9 MPa、46.5 MPa;粉煤灰采用镇江产Ⅰ级灰,细度10.0 %,烧失量2.4 %,三氧化硫 1.15 %,表观密度为 2 520 kg/m3;S95 级矿粉流动度比为98 %,含水量为0.17 %,表观密度为2 870 kg/m3;粗骨料采用粒径5 ~16 mm 连续级配的石子,表观密度为2 720 kg/m3,压碎值为9.99 %;细骨料选用细度模数为 2.584 、Ⅱ级配区砂,表观密度为2 330 kg/m3;减水剂选用聚羧酸高效PCA-9;拌和水选用本地自来水。
1.2 试验方法
水胶比分别为 0.52、0.48、0.44、0.40,粉煤灰掺量23 %,矿粉掺量18 %,砂率48.8 %,高效减水剂1.1 %,按表1 的配合比配制试件,试件尺寸为100 mm×100 mm ×100 mm。待试件养护(标养)7 d、14 d、28 d、56 d、84 d、112 d 时,取出进行超声波速测定,然后测试抗压强度。超声波速采用NM—4B—1609 仪器进行对测法测试。
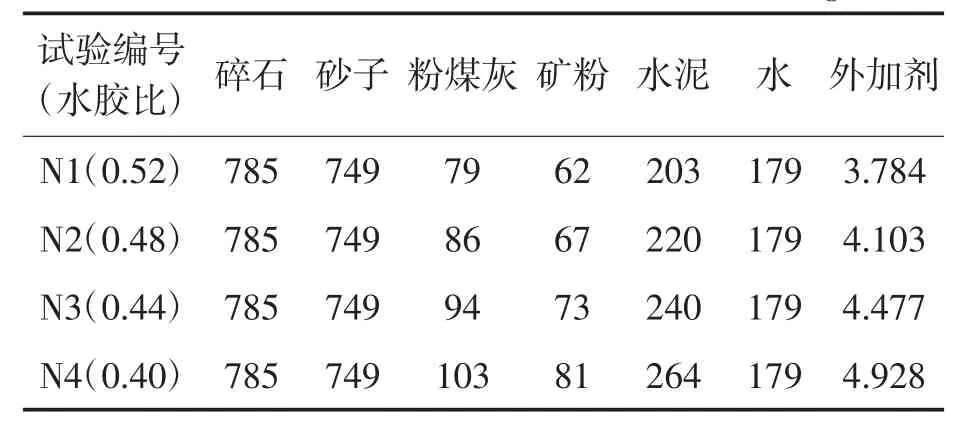
表1 自密实混凝土配合比 (kg/m3)
2 试验结果及分析
2.1 性能测试结果
依据JGJ/T 283-2012《自密实混凝土应用技术规程》测试了拌合物的各项性能,结果如表2 所示。

表2 性能试验测试结果
四组拌合物外观性能均表现为均匀,不泌水。由表2 可见,每组坍落扩展度达SF2 等级,扩展时间T500达到VS1 等级,填充性能好;间隙通过性指标达到PA1 等级;中边差小于2 cm。表明砂率选取合理,粗细骨料相互分散得比较好。以上指标均表征四组拌合物对于一般混凝土结构适用。从U型箱试验数据看,试件N4 的流动性和通过性能弱于前三组,原因可能是胶凝材料用量比例增加,使其黏性增大。
2.2 抗压强度、波速试验结果及分析
测试了 7 d、14 d、28 d、56 d、84 d、112 d 时试件的抗压强度与超声波速,结果如表3 所示。
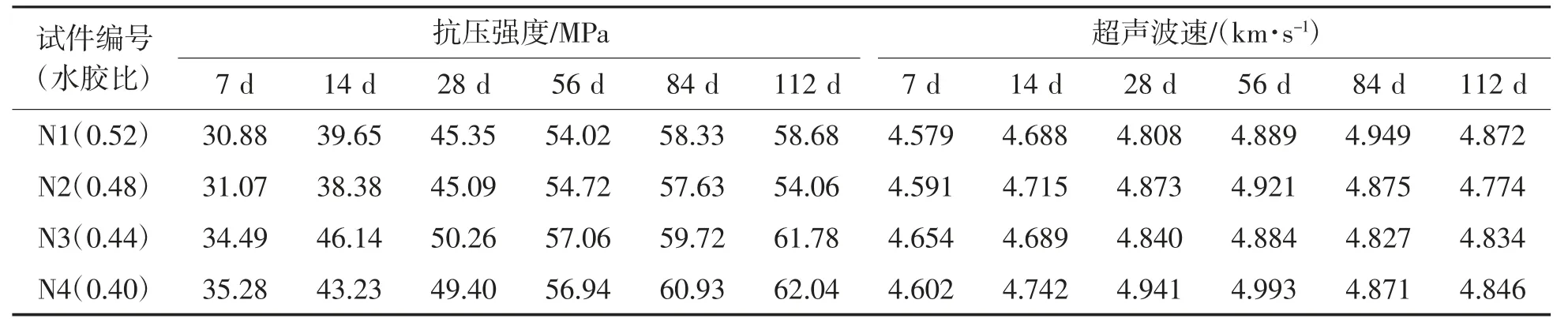
表3 不同龄期时的自密实混凝土强度及超声波速
2.2.1 强度与龄期的关系
不同水胶比试件的抗压强度随龄期变化趋势见图1。从图1 可知,试件强度均随龄期延长不断增大,前期增加趋势明显,后期增加缓慢;当养护龄期达84 d 后,其数值几乎保持稳定,112 d 与84 d 相比,强度最大增幅为 3.45%,最小仅增 0.6%;由于龄期112 d、水胶比0.48 的试件缺棱,且中间有马蜂面,故其强度有所降低。

图1 自密实混凝土抗压强度随龄期的变化趋势
由表3 可知,在同一龄期时,水胶比为0.52、0.48 的试件强度相差甚微,相差最大是龄期112 d时,水胶比 0.48 试件强度比 0.52 低 7.87 %,最小是28 d 时,仅低0.57 %,且增长趋势基本一致。试件 N3(0.44)、N4(0.40) 的强度比 N1(0.52)、N2(0.48)强度高,但四组试件表现出一致的特征,强度相差最大是龄期 14 d 时,试件 N4(0.40)比 N3(0.44)低 6.31%,最小的是养护龄期 56 d 时,仅低0.21%。由此可见,自密实混凝土受性能影响,强度对水胶比反应没有普通混凝土灵敏。试件的水胶比相差值小于0.04 时,低水胶比的自密实混凝土强度未必高。
2.2.2 超声波速与龄期的关系
试件超声波速随龄期的变化趋势见图2。从图2 可以看出:在龄期56 d 前,水胶比为0.48、0.44、0.40 的试件波速均随龄期的延长不断增大,之后波速开始大幅下降,至龄期84 d 后下降趋势转向平稳;水胶比为0.52 的试件在养护龄期84 d前,超声波速不断增大,84 d 后则开始大幅下降。超声波在水和空气中传播速度比在固体中慢,早期试件中胶凝材料水化不完全,孔隙中含水较多,而随着养护龄期的延长,试件中胶凝材料渐渐水化,在此过程中不断消耗水分,且水化产物不断充实孔隙,与砂石包裹在一起,使试件内部越来越密实[13]。因此,早期波速不断增大,但56 d 后胶凝材料水化基本完成,水分被消耗,试件孔隙被空气或水化产物填充,这时超声波在试件中因遇到气相、固相发生反射或绕射,导致波速下降[14]。
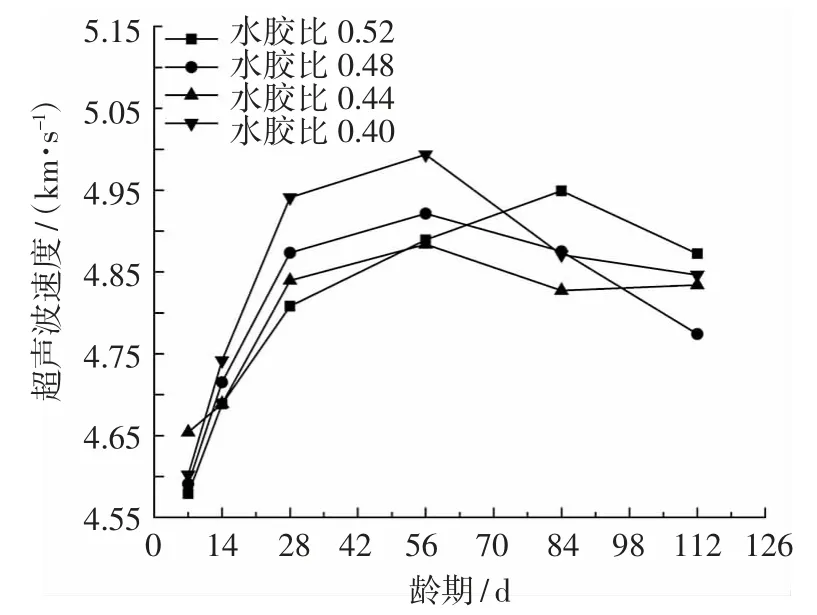
图2 自密实混凝土超声波速随龄期的变化趋势
由图2 还可见,龄期56 d 内,在同一龄期时,水胶比为 0.40 的试件波速比 0.44 的大,水胶比为0.48 的试件波速比 0.52 的大,但是龄期超过 56 d后,水胶比0.52 的试件波速最大。这是因为用水量相同,胶凝材料用量少,孔隙水被消耗需要更长时间,所以波速下降较滞后。
2.3 强度与超声波速关系
从图1、图2 看出,同一养护龄期时,水胶比为 0.40、0.44 的试件强度高于水胶比为 0.48、0.52的试件强度,而波速不一定高于其;在养护龄期56 d 前,试件的强度与波速皆随龄期延长而增大,56 d 后强度增长缓慢,波速降低。由此可见,在合适的龄期内,强度与波速有显著的内在联系。
考虑利用波速预测强度。为提高预测的精确性,对水胶比为0.52 的试件分析龄期84 d 内的情况,其余试件分析龄期56 d 内的情况。基于此,模拟出各水胶比试件的超声波速与抗压强度之间的函数关系,如表4 所示。通过对比函数系数发现,不同水胶比的自密实混凝土函数模型相同,系数不同。可见当波速相同时,不同的水胶比试件对应的强度数值不同。因此,需要分别对不同强度等级的自密实混凝土做回归方程。

表4 自密实混凝土超声波速与抗压强度之间的函数关系
图3—5 分别为试件波速与强度之间函数关系的相关系数(R2)、调整后相关系数和均方根误差。图3 表明,不同水胶比的试件,二次函数的相关系数相对较好。为消除因增加自变量而高估R2,则引入调整后的R2,增加评判模拟曲线精度的准确性。从图 4 可见,试件 N 1(0.52)幂函数调整后相关系数最大;试件 N 2(0.48)、N4(0.40)则是指数函数调整后相关系数最大;试件N3(0.44)是线性函数调整后系数最大。可见,不同水胶比对应最优的拟合曲线不同。为验证以上模拟精度的最优值,计算各模拟曲线的均方根误差,如图5 所示,也验证了上述结论。
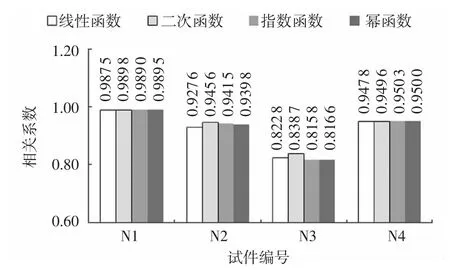
图3 波速与强度函数的相关系数
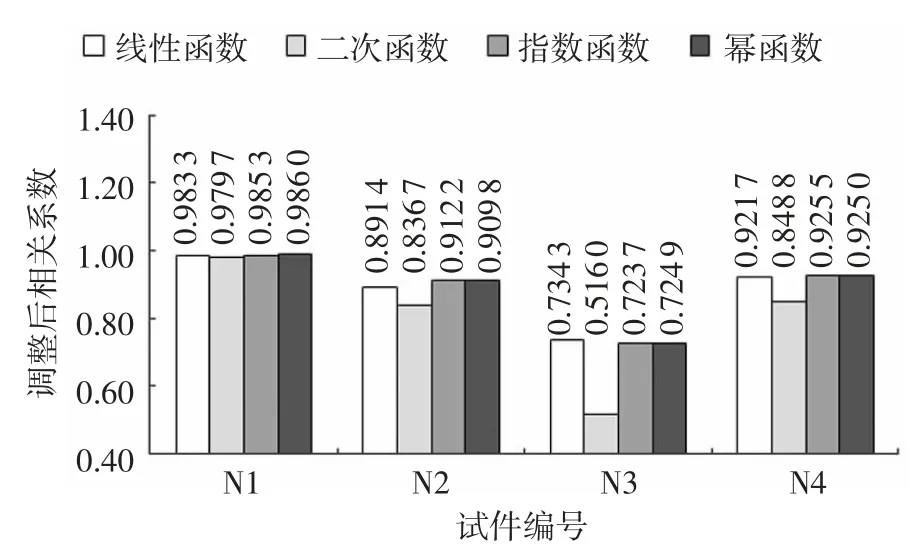
图4 波速与强度函数调整后的相关系数
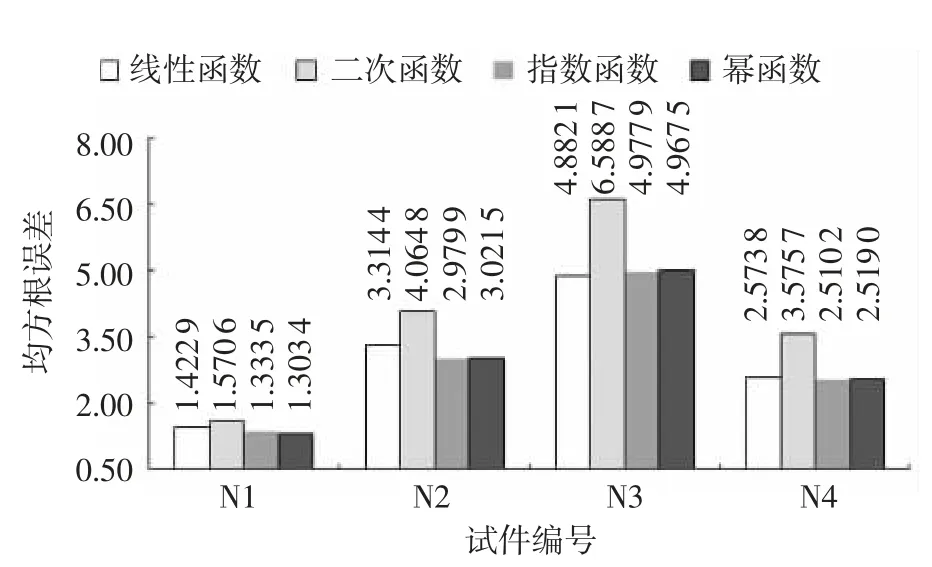
图5 波速与强度函数的均方根误差

图6 不同水胶比试件波速与强度的函数关系模拟曲线
图6 是不同水胶比试件波速与强度的函数关系模拟曲线。图6 表明,四组试件的波速均随强度的增加而增大,龄期14 d 内和28 d 后相对增长速率高于龄期14~28 d。由于增长速率不一致,模拟曲线用一次性函数表示,精度不是最高。虽然不同水胶比试件强度与波速关系表现出了一致的特征,但在不同龄期阶段强度与波速两者相对关系变化速率不同,因此对于不同水胶比要用不同的模拟曲线来表征。
3 结 论
(1)受性能影响,自密实混凝土在水胶比相差小于0.04 时,低水胶比的强度未必高;强度随着龄期延长不断增大,初期增长速率较后期大,在龄期84 d 后,强度基本保持稳定,增长较缓慢。前期由于粉煤灰与矿粉两种掺量的物理与化学叠加效应,促使强度增长迅速,但是在龄期56 d 后,两种协同效应影响力降低,水化反应也基本完成,从而强度趋于稳定[15]。
(2)自密实混凝土波速随着龄期增长表现出先增加后下降特征;在龄期56 d 后,水胶比为0.48、0.44、0.40 的自密实混凝土波速开始下降;在龄期84 d 后,水胶比为0.52 的自密实混凝土波速开始下降。
(3)在一定龄期内,不同水胶比的自密实混凝土的超声波速与强度呈强相关性。建立无损模拟曲线方程,为预测适用本地区低水胶比自密实混凝土强度提供了理论支持,也为检测加固工程中的自密实混凝土质量提供了参考依据。
(4)波速随强度增大而增大,但是由于水胶比不同,粉煤灰与矿粉用量不同,其对强度与波速的影响效应不同,造成其在龄期14~28 d 时,波速随着强度增长的速率明显不同。因此,不同水胶比的自密实混凝土的模拟曲线不同:水胶比为0.52 的自密实混凝土以幂函数的拟合性最好;对于水胶比为 0.48、0.40 的自密实混凝土,用指数函数拟合最佳;水胶比为0.44 自密实混凝土,线性函数拟合最优。
