基于改进MSD法的软土深基坑支护侧移规律

苏秀婷, 陈 健, 高文龙, 乔阿龙, 杜昌言

(1.上海勘察设计研究院(集团)有限公司青岛分公司, 青岛 266000； 2.中国海洋大学环境科学与工程学院，青岛 266100； 3.中铁十四局集团有限公司, 济南 250101； 4.青岛城阳方正市政工程有限公司， 青岛 266000；5.中铁十四局集团大盾构工程有限公司, 南京 211800)

在软土地层中建造大型深基坑工程往往面临着较大的施工风险[1]，基坑围护结构更易发生变形[2-3]。因此，深刻认识软土地层中基坑的变形规律，掌握准确而有效的基坑变形预测方法，对基坑的设计和施工是非常重要的。目前已有的基坑变形预测手段往往存在一定局限性，如经验公式法常因土层差异而产生较大误差；反向传播(back propagation，BP)人工神经网络、支持向量机等人工智能方法受限于完成的监测数据和学习过程，同样会存在较大误差。

可动强度设计(mobilizable strength design，MSD)法是基坑变形预测常用的方法，该方法是由Osman等[4]在悬臂形基坑开挖塑性变形机制以及基坑体系内的能量守恒原理的研究基础上提出的，此后Bolton等[5]基于O’Rourke[6]的研究成果，使用MSD法计算了含内支撑的基坑工程，在结合了变形增量法和能量守恒原理两大基础理论的情况下，又将施工现场土的各向异性和不排水抗剪强度纳入计算。王浩然等[7]研究了围护墙结构自身发生弯曲应变时的做功，补充了MSD理论的能量守恒体系。刘美麟等[8]基于施工现场的经验数据，进一步改进了基坑变形机制，补充了MSD基坑变形理论。马元等[9]在总结杭州典型狭长软土基坑实测数据基础上，采用修正强度发挥解析预测理论的MMSD法，计算了基础典型断面支护侧移规律，并与实测数据进行对比分析，研究结果表明，该方法可较好地预测杭州地区狭长形基坑支护侧移规律。

MSD方法是一种有效、实用且更有待发展的基坑变形预测方法，但其包含的能量守恒体系仍不够完善，因此，现总结已有的MSD基坑变形预测理论，补充该理论的计算方程，将对软土地区深基坑工程施工具有较大的参考价值。同时，借助有限元分析法作为辅助手段，进一步完善软土地层基坑变形预测体系[10]。

1 工程概况及地质条件

1.1 工程概况

以济南黄河隧道北岸工作井基坑工程为依托，济南黄河隧道(济泺路穿黄隧道)位于济南市北部，为超大断面盾构法隧道。为满足盾构机吊装及始发的需要，北岸始发井基坑宽度设计为34.14～50 m，长度为152.2 m，开挖深度为31.2 m，如图1所示。

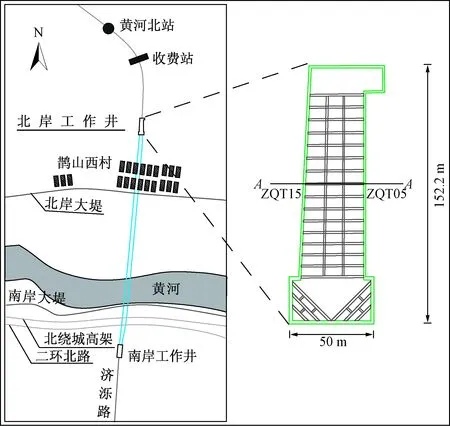
图1 济南黄河隧道始发井概况Fig.1 General situation of the starting shaft of Jinan Yellow River Tunnel

1.1.1 围护结构

基坑围护结构采用地下连续墙，顺作法施工，地下连续墙厚度1.2 m，深度47～51.5 m，采用水下C35钢筋混凝土浇筑，接缝处使用H型钢联结。

1.1.2 内支撑

根据工程设计，基坑分五次开挖，在基坑不同位置分别设置5、7道支撑，大盾构始发井处为7道钢支撑+混凝土支撑，始发段为5道钢支撑+混凝土支撑，始发段A-A监测断面的5道支撑的设计及施工步骤如图2、表1所示。

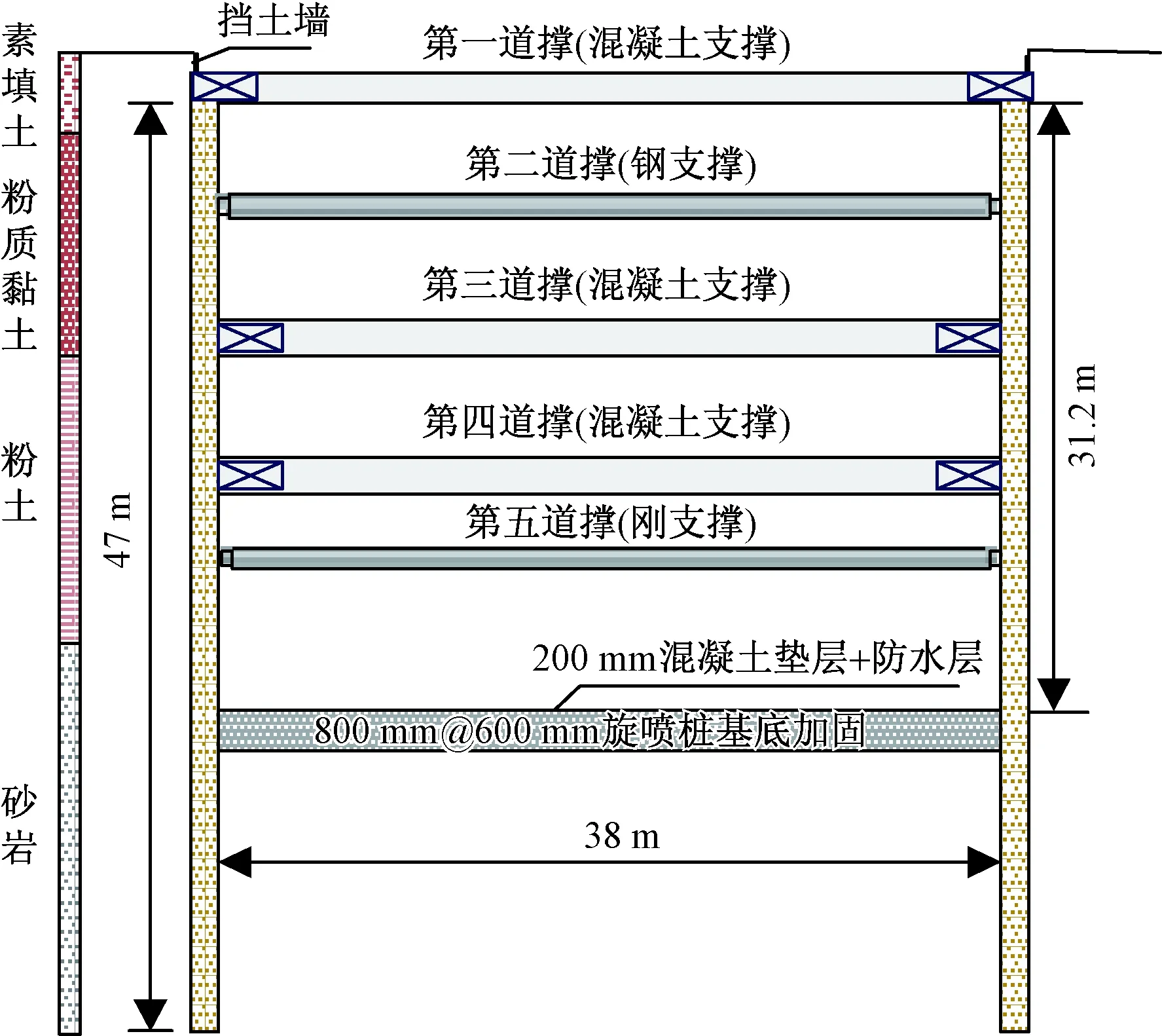
图2 A-A断面设计图Fig.2 Design drawing of A-A section

表1 施工步骤

1.2 工程地质条件

该基坑工程地处冲积平原，局部微地貌单元系黄河河床，原始地形较平坦，地形略有起伏。根据钻探揭露，表层局部为人工填土，向下依次为第四系全新统冲积、冲洪积粉质黏土、粉土、砂层及中生代燕山期晚期侵入岩辉长岩，土质情况较差。基坑所在地层以粉质黏土、粉土为主。

1.3 水文地质条件

该基坑工程所处地貌单元为黄河Ⅰ级阶地，地表水主要为黄河河水、鹊山水库及鱼塘、水塘等，地下水埋深在1.10～1.70 m，地下水类型为第四系松散覆盖层的孔隙潜水，含水层主要为人工填土、粉质黏土、粉土、砂层等。其中粉质黏土属微透水层，粉土属微～弱透水层，砂层属中等～强透水层。

2 改进MSD法变形预测

MSD理论是一种以能量守恒为基础的变形分析理论，由于此方法基于一定的研究基础，一般适用于软土地层条件下、支护结构为地下连续墙结合内支撑的基坑刚性变形或柔性变形。

2.1 基坑变形机制

2.1.1 坑周土体变形机制

岩土工程学者Lam等[11]在基坑开挖和施作内支撑时，将基坑周围土体的形变划分成四个区域：长方形ABCD、扇形CDE、扇形EFG以及三角形FGI。基坑各深度位置上土体形变机理如图3所示，在开挖并施作内撑时，围护结构产生位移形变，同时伴随着坑周地面的沉降。在地层内部，四个区域内的土体表现为余弦函数变形，由变形传递规律可知，围护墙水平位移量等于该位置墙后产生的地面沉降大小。在图3中，每个箭头上变形的大小始终稳定，并向后方的位置传递。

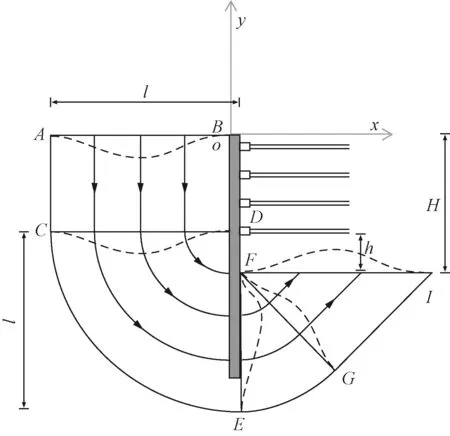
l为形变影响区域的宽度范围，m；H为基坑深度，m；h为最下方的内支撑到基坑地板的距离，m图3 基坑变形分区及基坑变形增量机制Fig.3 Deformation increment mechanism of internal support foundation pit

在矩形ABCD中，水平和垂直方向的变形计算公式分别为

(1)

式(1)中：Δwmax为工程中围护墙结构形变的峰值，m；Δwx为围护墙结构在水平方向的形变，m；Δwy为围护结构在竖直方向的形变，m。

2.1.2 基坑围护结构变形机制

根据地质条件，一般每开挖3～5 m就设一道支撑，此后再进行下一步开挖。O’Rourke等[6]指出，单次向下挖掘某道内撑下方岩土体过程中，围护墙结构将产生类似余弦函数的水平形变Δw(图4)，Δw计算方法为

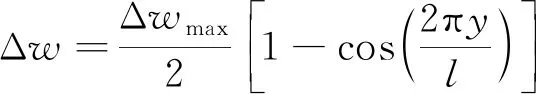
(2)

l=αs

(3)

式中：Δw为在当前施作的内撑下方区域某位置围护墙结构水平位移变化值，m；s为当前施作的内撑和围护墙最底端的距离，m；α为形变范围系数，较硬质地层中α=1，软黏土中α=2。在现场施工时，地下连续墙基本处于这两者之间的地层状况中，地下连续墙在深度方向上发生的峰值变形一般紧靠工程的开挖面[12]，一般可以认为1<α<2[13]。

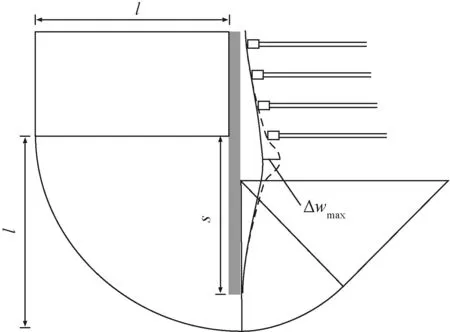
图4 连续墙水平位移增量图Fig.4 Increment of horizontal displacement of internal support foundation pit

2.2 改进MSD理论中的基坑能量守恒

改进MSD理论认为土体抗剪强度与剪应变表现为函数关系。当工程施工时，场地土体的应力状态受到扰动，产生了直接施加于围护墙的土压力场，在力的作用下，围护墙结构发生了变形和位移。同时坑周土体也具有相对运动的趋势，这一趋势必然将伴随内力的产生，即剪应力。当位移发生时，土体内力做功，基坑体系之中发生了能量的守恒转换。在工程的全部施工周期，整个工程始终遵守能量守恒定律，外力(重力)做功始终等于内力做功。土体内力做功一方面表现为剪应力做功，另一方面还包括内支撑压缩变形时内力做功和围护墙结构发生弯曲变形时的内力做功，前者以压缩弹性势能的方式存储于内支撑中，后者以弯曲变形能的方式存储于围护墙结构中。

改进MSD 理论与原理论的区别主要在于，改进MSD 理论在原有的能量守恒方程中引入了墙体自身的弯曲应变能和内支撑的压缩弹性势能，充分考虑了施工环境内不同土层的物理力学性质，并考虑了支护结构与土体的相互作用，还考虑了土体不排水抗剪强度的动态发展，使得改进MSD理论更加完善和可靠。

2.2.1 土体重力做功

在基坑开挖的过程中，基坑开挖到底时总重力势能变化量为W，开挖到第m阶段时重力势能变化量为Wm，此时土体重力做功的计算公式为

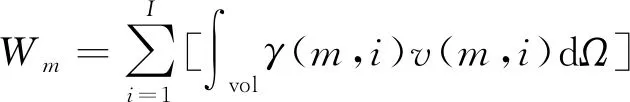
(4)

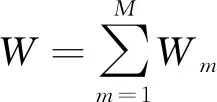
(5)

式中：Ω为变形区域的影响范围；i为工程施工现场的土层，总层数为I；m为基坑工程施工设计层数，总开挖为M层；γ(m,i)为第m次开挖、第i层土的平均重度；v(m,i)为第m次开挖施工时、第i层岩土体的垂向位移变化量。通过将开挖的土层分成多层，就可以更加准确地计算各个阶段累积后的土层外力所做的功，得到基坑开挖影响范围内土体总重力势能的变化量。

2.2.2 土体剪应力做功

在基坑开挖施工过程中，向下开挖至一定深度处，这一阶段基坑的变形为整个基坑体系，包括坑周的土体以围护墙底端为中中心，做三角形转动，其中围护墙做非变形的刚性转动，如图5所示。

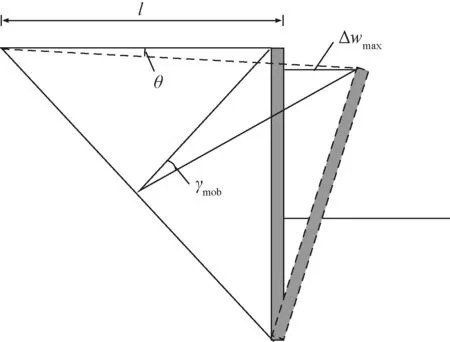
θ为整个基坑体系刚性变形的转动角；γmob为土体表观剪应变，其大小等于2θ图5 悬臂型基坑变形增量机制Fig.5 Deformation increment mechanism of Cantilever foundation pit

通过表观剪切强度系数与表观剪应变增量拟合函数即可得出γmob，即

γmob=2Δθ

(6)

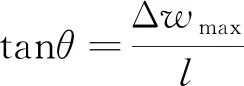
(7)

由于基坑开挖时转动角极小，根据式(7)，得

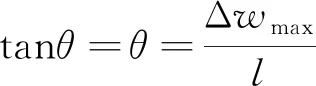
(8)

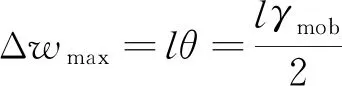
(9)

在基坑施工中，当岩土体发生塑性形变，而无相对滑移时，土体内的剪切强度并未到达应有的抗剪强度cu，将此时表现出来的抗剪强度定义为不排水抗剪强度的表观值cmob。将表观抗剪强度系数β(m,i)定义为不排水抗剪强度表观值cmob与真实抗剪强度cu的比值，即

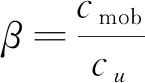
(10)

认为施工过程在坑周土体不排水的条件下进行，土体剪应力做功(即基坑体系的内力做功)，剪应力做功的计算公式为

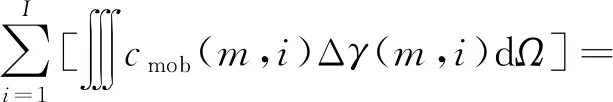
(11)

式(11)中：Δγ(m,i)为第m次开挖地层时，第i层土的固结不排水情况下的剪应变增量。采用该计算公式，可以计算得出基坑开挖过程中坑内各层土内力做功情况。

2.2.3 围护墙体的弯曲应变能

王浩然等[7]在原有MSD方法的研究上引入了围护墙弯曲变形储存的变形能P这一概念，并考虑了土体的各向异性，发表了王浩然改进MSD理论。P可通过围护墙结构抗弯刚度E和围护墙水平位移变形增量值Δw积分得到，计算公式为

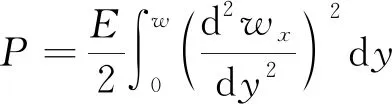
(12)

将式(1)代入式(12)，得

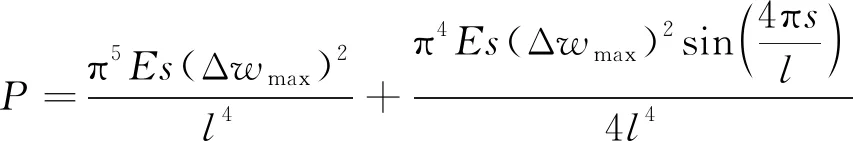
(13)

2.2.4 内支撑压缩弹性势能

刘美麟等[8]提出基坑内支撑的压缩弹性势能V这一概念，V的计算公式为

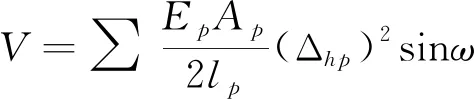
(14)

式(14)中：EpAp为第p道支撑的抗压刚度；lp为该道内支撑的长度；ω为该内支撑与基坑侧壁的夹角，对于垂直于基坑内壁的支撑，sinω=1；Δhp为该道支撑在此位置的变形量，等于基坑围护墙结构在该位置的变形量。

在基坑工程施工开挖期间，存在的能量守恒关系为：土体外力(重力)做功W等于土体内力(剪应力)做功U、围护墙的弯曲变形能P与内支撑的压缩弹性势能V之和，即

W=U+P+V

(15)

2.3 改进MSD法变形计算

济南黄河隧道北岸工作井基坑围护墙结构主要嵌于较软弱的粉质黏土层，超固结比ROC=1，Bolton等[5]利用19种粉质黏土进行了100余组土工试验，统计分析给出了表观剪应变γmob与表观剪切强度系数β的关系，利用试验数据拟合出超固结比ROC=1时的γmob与β的关系为

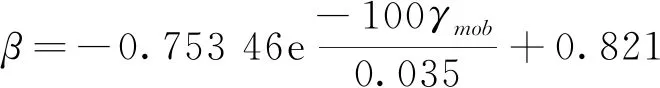
(16)

基坑所在软土地层变形区域影响系数取α=1.5，即开挖变形影响区长度l=1.5s。第二步施工时，既在2.1m位置施作第一道支撑(砼支撑)后，开挖至7.7m深，此时土体是为粉质黏土，重度γ=19.5 kN/m3，此支撑离围护墙趾长度s=37 m，即开挖变形区影响长度l=1.5，s=55.5 m。根据式(8)、式(9)、式(11)可分别计算出各层土体重力做功和剪应力做工，进行累加后，重力和剪应力做工分别为

W=2 280Δwmax

(17)

U=4 357βΔwmax

(18)

已知该盾构工作井围护墙结构抗弯刚度E=1 037.7 kN/m2，第一道混凝土支撑的抗压刚度EpAp=1 716 MN/m，支撑的有效长度lp=35 m，根据式(13)、式(14)计算得到此时围护墙弯曲应变能和内支撑压缩弹性势能为

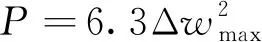
(19)

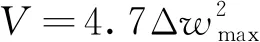
(20)

根据式(4)，则有

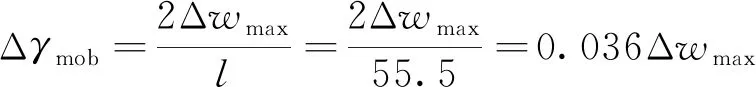
(21)

根据式(15)、式(16)、式(21)，可求得第二层土体开挖时墙体最大水平位移Δwmax=4.3 mm。

同理可求得：第三层土体开挖时墙体最大水平位移Δwmax=6.3 mm；第四层土体开挖时墙体最大水平位移Δwmax=10.2 mm；第五层土体开挖时墙体最大水平位移Δwmax=7.1 mm；第六层土体开挖时墙体最大水平位移Δwmax=11.2 mm。

按照MSD法基坑变形理论，计算出每一个阶段的最大位移量，根据式(2)得到各个开挖步骤的墙体水平位增量，绘制出围护墙的位移曲线，如图6所示。

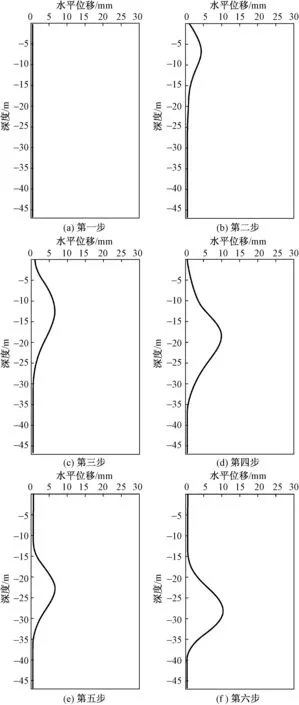
图6 各步骤连续墙水平位移计算结果Fig.6 Calculation results of horizontal displacement of continuous wall in each step

将上述所有位移图像叠加，获得改进MSD 法对围护墙水平位移的最终计算结果，如图7所示。在深度方向上，围护墙水平位移表现为先增大后减小的分布，位移最大值出现在连续墙28.5 m 深处，位于第五道支撑以下5 m、基坑基底以上2.7 m 位置，最大位移值约28 mm，约等于0.06%H，这一结论与大多数学者的研究结果相符。

3 有限元分析法变形预测

除采用改进MSD法外，还通过有限元分析法对济南黄河隧道北岸工作井进行变形预测，对改进MSD法的预测结果加以佐证。

3.1 建立模型

模拟计算采用Midas-GTS/NX三维有限元数值计算软件进行，模型尺寸依照真实工程状况而建，模型尺寸为350 m×180 m×100 m，开挖的基坑模型位于土体模型的正中心。基坑模型长151 m，宽19～33.2 m，深20～28 m，围护墙深40 m，如图8所示。

图7 连续墙变形叠加Fig.7 Deformation superposition of continuous wall

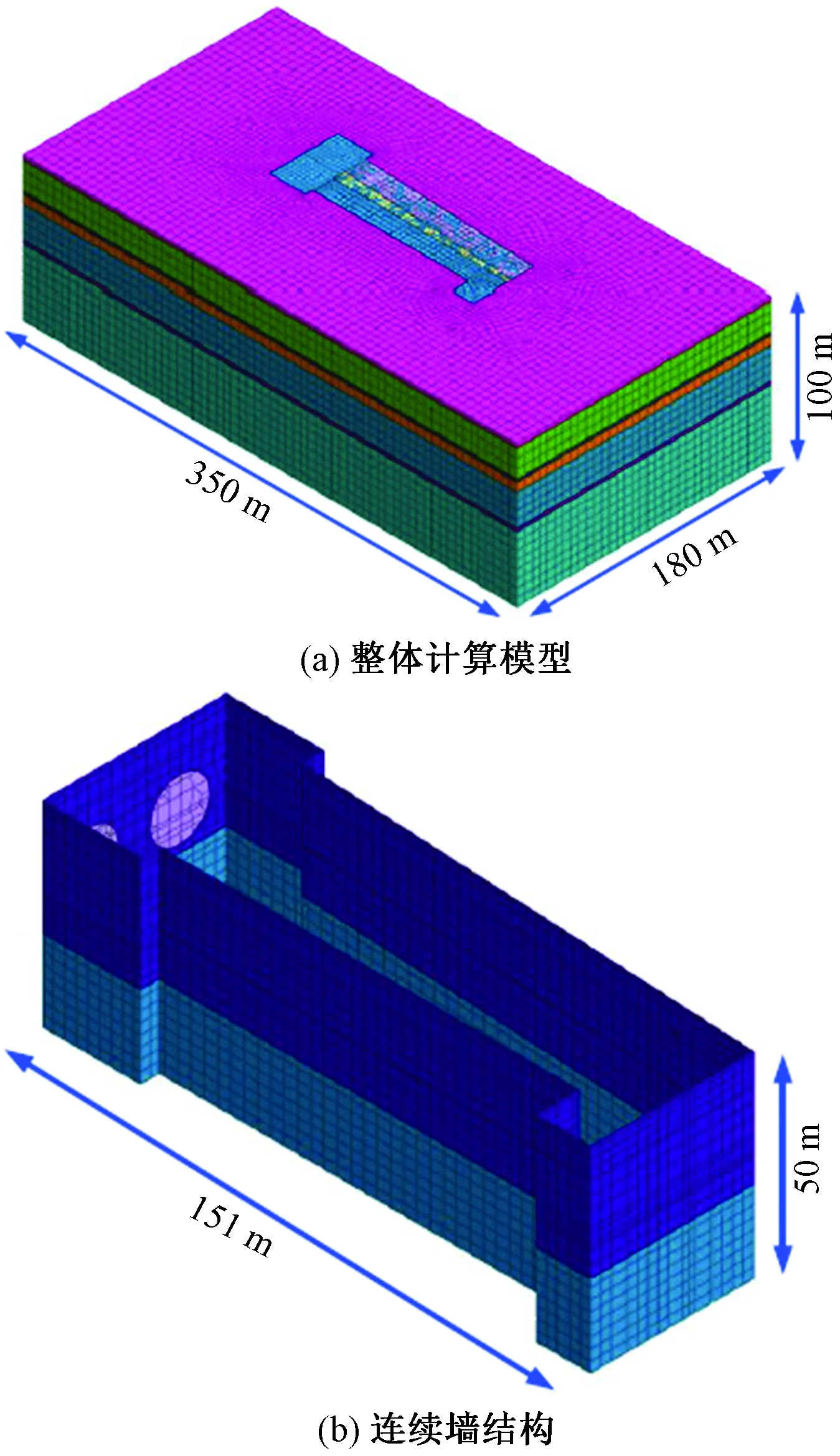
图8 数值模拟计算模型Fig.8 Numerical simulation model

土体使用修正摩尔-库伦模型(modified Mohr-Coulomb)，该模型是在原有摩尔-库伦模型(Mohr-Coulomb)的基础上加以改善，涵盖了土体的剪胀性、剪切硬化以及卸载/重新加载模量，采用摩擦硬化特性来模拟在偏应力下的塑性剪切应变，同时采用帽型硬化来描述主应力压缩的体积变形，当材料初始屈服后，在原有的屈服面上将产生多个继生屈服面，可以较为有效地对基坑挖掘过程进行模拟。土层参数参考地勘资料选取，如表2所示。

围护结构为线性弹性材料，计算参数如表3所示，地连墙、侧墙、及各层楼板均采用板单元模型，各层腰梁、抗拔桩及立柱等结构均采用梁单元模型，各结构均按照设计施工图纸进行定义。

表2 土层计算参数

表3 其他材料计算参数

3.2 有限元法变形计算

在施工工况设置中，首先进行地应力平衡，将各土层因重力产生的位移进行清零，只保留地层应力，模拟实际地层的真实情况。然后根据真实的施工阶段进行设置。

计算完成后，将地层及各部分结构的变形值进行结果提取，工作井主体结构施作各部分地层及结构变形预测如图9所示，ZQT05监测点处的墙体水平位移曲线如图10所示。北岸工作井主体各部分结构施工过程中，基坑四面墙体均发生侧向位移，位移方向均为向基坑内部移动(累计变化量为正值)，在深度方向上，位移量表现出先升高后降低的分布趋势。基坑的两条长边对应的连续墙变形趋势极为相近，每面连续墙的位移峰值均发生在墙体中部偏下的位置，也就是在第五道支撑的下方、基坑基底以上，埋深27～28 m处，峰值为+16.9 mm，约为0.036%H。

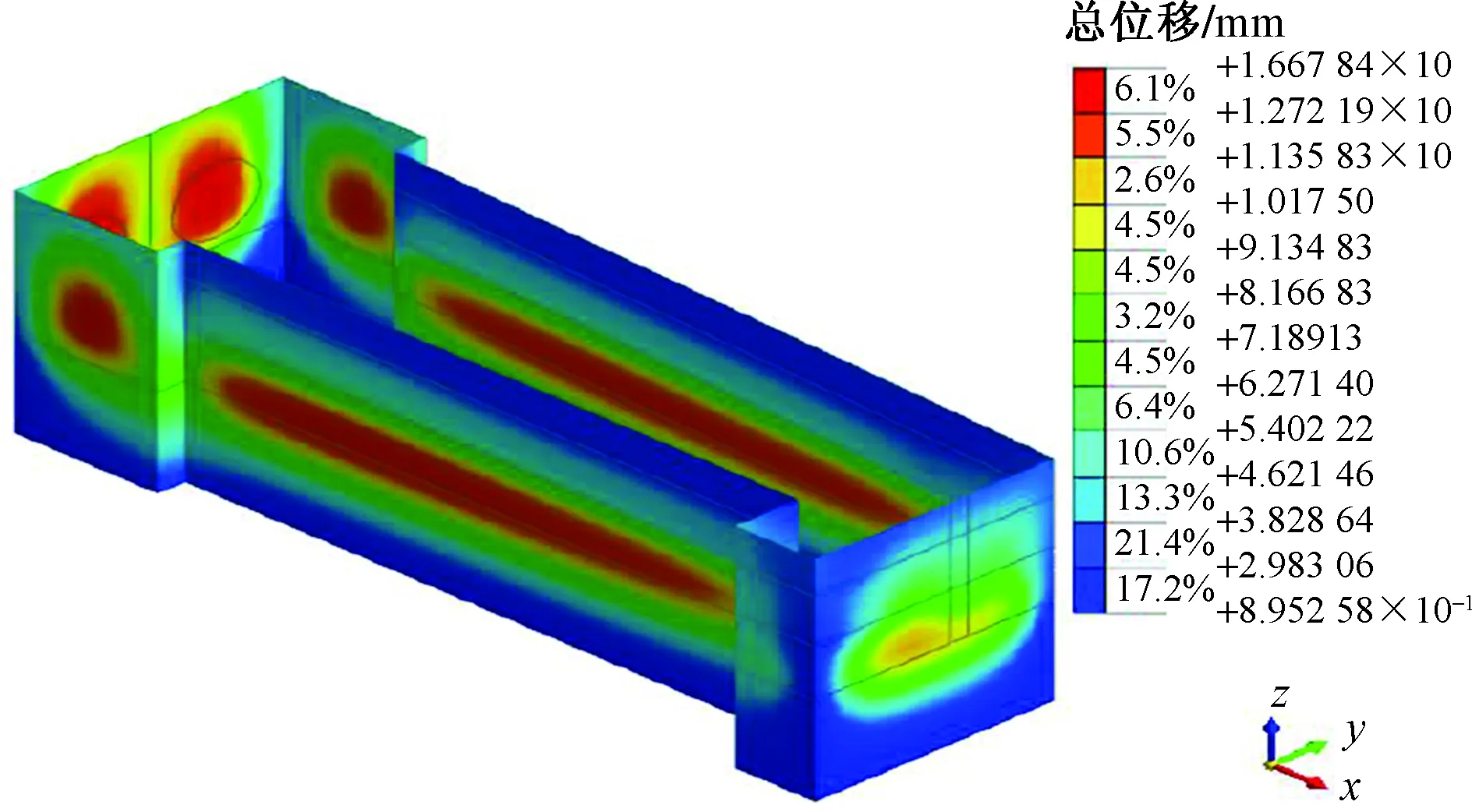
图9 连续墙变形云图Fig.9 Continuous wall deformation cloud chart

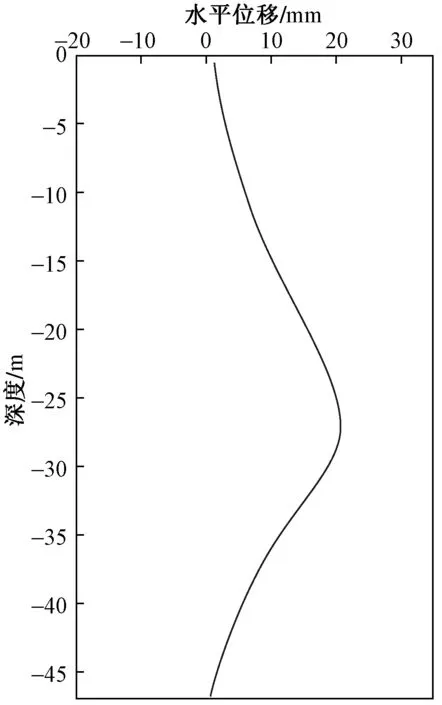
图10 连续墙水平变形预测Fig.10 Prediction of horizontal deformation of continuous wall

4 现场监测数据分析

4.1 监测点布设

围护墙深层水平位移能定量地反映地下连续墙在深度方向上的变形情况，是最直接、最有效的地下连续墙变形监测项目。一般在围护墙特征位置处应设置深层水平位移监测点，例如基坑边缘的中部以及阳角处，相邻监测间距应控制为20～50 m。在基坑工程地下连续墙施工作业中，预先将测斜管与钢筋笼绑扎并随之一起浇筑成墙，如图11所示。

图11 围护墙深层水平位移(测斜)的布点示意Fig.11 Layout of horizontal displacement monitoring points in the deep layer of retaining wall

4.2 监测数据分析

图12和图13分别反映了监测点ZQT05和ZQT15(图1中AA监测断面)在各层土体开挖后的围护墙深层水平位移状况。

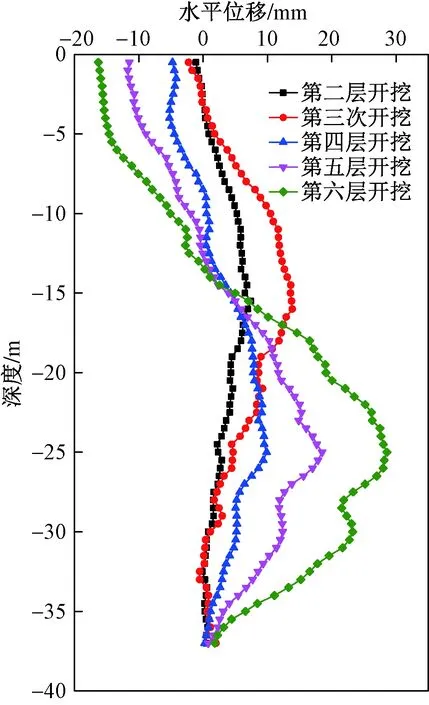
图12 监测点ZQT05围护墙深层水平位移情况Fig.12 Change of deep horizontal displacement of enclosure wall at monitoring point ZQT05

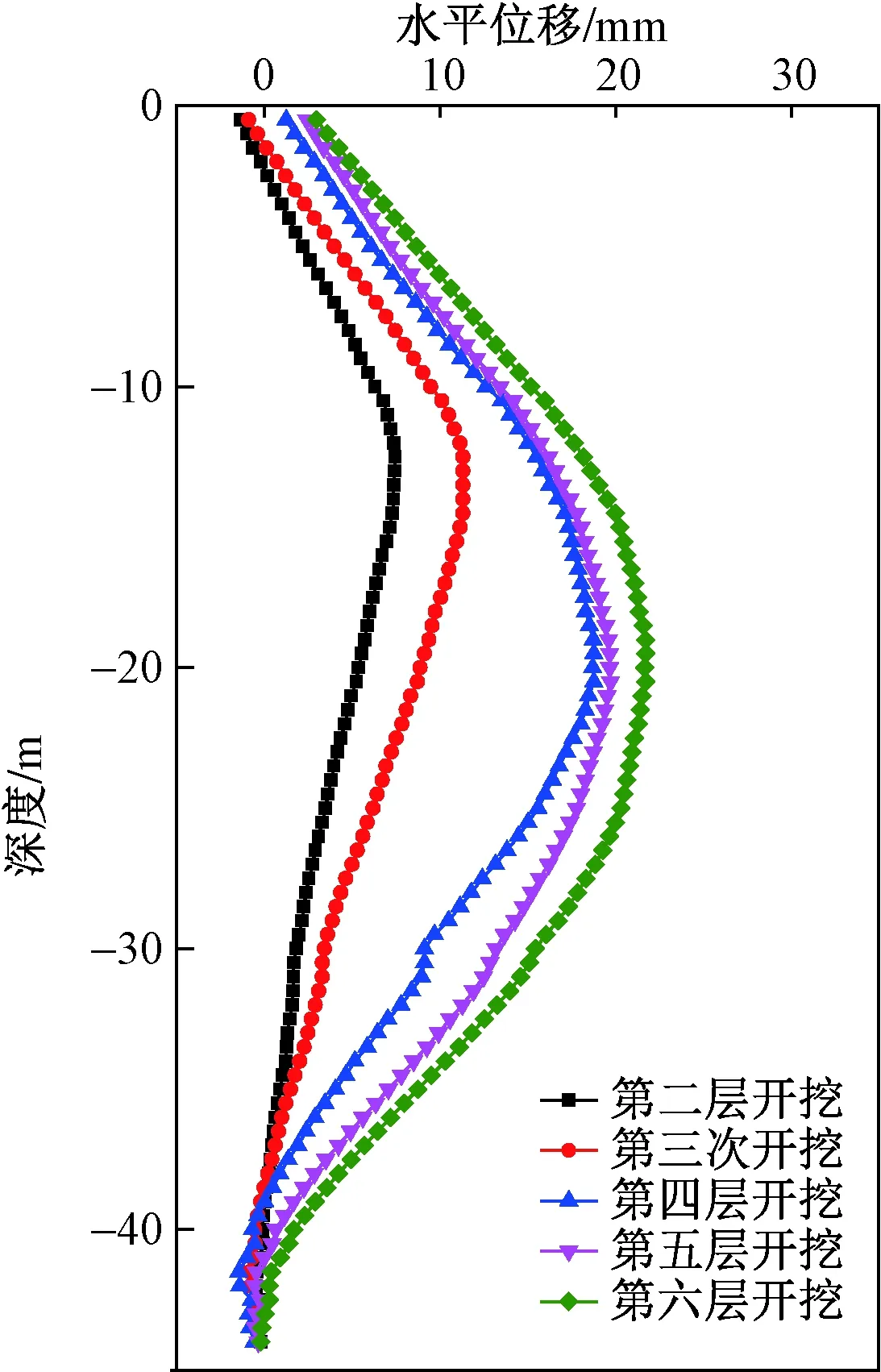
图13 监测点ZQT15围护墙深层水平位移情况Fig.13 Change of deep horizontal displacement of enclosure wall at monitoring point ZQT15

在监测点ZQT05位置处，开挖第二层土体并设置次道混凝土支撑后，位移峰值位于约13 m处，峰值约为6 mm；再次开挖施工并施作下道钢支撑后，位移峰值下移至约15 m处，峰值增加至11 mm；基坑开挖完成后，位移峰值增至约28 mm，位置位于26 m深处。在监测点ZQT15位置处，开挖第二层土体后，位移峰值位于约11 m处，峰值约为5.5 mm；继续开挖第三层土体后，最大位移增加至10.5 mm，位置下移至约13 m处；开挖第三次土体后，最大位移增至18 mm，位置下移至约20 m处；基坑开挖完成后，最大位移增加至21 mm，位置下移至22 m处。综上，基坑开挖各阶段连续墙的变形峰值及峰值位置与改进MSD法的计算值较为相符。

总结围护墙深层水平位移沿挖掘深度方向上的变形规律，可知围护墙的深层水平位移主要受到挖掘深度的影响，还可能受到围护结构形式、刚度、嵌入土层深度和内支撑预应力的影响。在开挖作业过程中，围护墙结构水平位移持续变大，且开挖越深，位移峰值坐标也逐渐向下移。

5 改进MSD法、有限元分析法与监测数据对比

5.1 数据曲线的趋势

为了验证改进MSD法和有限元分析法在实际工程中的计算效果，将改进MSD法、有限元分析法所得的围护墙变形预测曲线与监测数据进行对比，结果如图14所示。

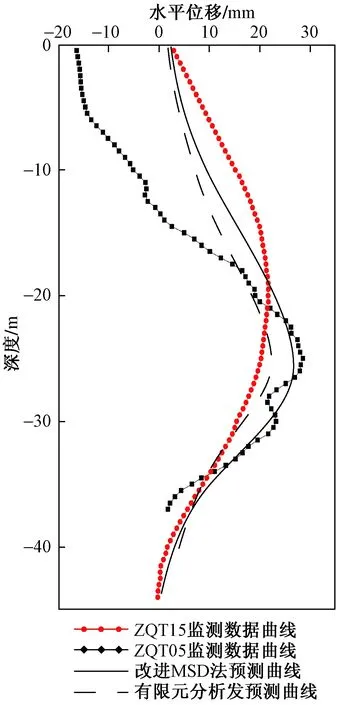
图14 预测值与监测值对比Fig.14 Comparison between predicted value and monitored value

图14中显示，在对基坑长边中心点位置进行变形预测时，使用改进MSD法、使用Midas软件的有限元分析法的预测结果和实际监测数据的变形趋势、峰值位置基本相同，都随深度呈先变大，后减小的“大肚子”形分布，峰值均出现在第五道支撑以下、埋深约28 m。同时改进MSD法对变形量的预测也较为准确，峰值较为接近，而有限元分析法得到的变形量要小于实际值。

综上，改进MSD法对围护墙变形预测的结果趋势相同、变形量较为接近、变形峰值及峰值出现的位置较为准确，可以得出改进MSD法对软土地层基坑的变形预测较为准确、合理。

5.2 主要预测误差来源

改进MSD法和有限元分析法只能计算基坑正常开挖和施加内支撑条件下的变形，而对于工程现场的其他影响因素，如地面荷载等无法纳入计算，一定程度上限制了这两种方法的应用范围，也造成了较大的误差。改进MSD法在引入内支撑结构弯曲应变能之后，对于施加预应力的钢支撑应力释放导致的围护墙变形未纳入计算，对基坑内支撑产生的弯曲变形能未能纳入能量守恒体系中加以计算，这也可能导致MSD理论最终的计算结果偏大。而数值计算方法的质量依赖于选定的土体本构模型和其他计算参数，往往有较大的误差。

5.3 预测误差控制

在针对特定工程的计算中，将场地的特殊施工条件，如降水、大型机械设备荷载等变形影响因素纳入计算，可减小误差。对改进MSD方法，可通过优化MSD理论的受力和能量守恒关系，将基坑施工中可能存在的其他形式的受力和变形能，如钢支撑预应力、结构立柱的压缩变形能等引入计算，减小误差；还可通过获得更加精确的土层性质，优化土体的不排水抗剪强度求解方法等手段。对有限元分析法，可通过优化本构模型和地层参数、优化模型、材料数据等，可减小误差。

6 结论

(1)综合当前MSD理论研究的基础上，引入了墙体自身的弯曲应变能和内支撑的压缩弹性势能，完善了基坑变形的能量守恒体系，总结了一种改进的MSD方法。利用该方法分别求得基坑各步骤开挖时的连续墙水平位移曲线，将各个部分的曲线叠加，得到了最终的基坑围护墙水平位移曲线。

(2)利用改进MSD法和有限元分析法分别对济南黄河隧道北岸盾构工作井基坑工程进行变形预测，并与监测数据进行对比，发现两种方法的预测结果与现场实测值在趋势上高度相同，数值上比较接近，证实了改进MSD法虽仍有一些尚待解决的问题，但其总体具有较好的可靠性，配合有限元分析，可以较好地预测连续墙变形，对类似的工程具备较高的参考价值。

(3)改进MSD理论当前只能对明挖软土基坑正常开挖和支护过程的变形值进行计算，然而施工现场工况十分复杂，包括地下水排水降水、地面荷载等工况都难以考虑周全；同时，在计算内支撑能量时，只考虑了内支撑的压缩弹性势能，而未考虑内支撑可能发生的的弯曲变形，这仍有待于进一步深入研究。