基于联合仿真的板翅式换热器温度场研究
2021-05-06李斐然蒋彦龙詹宏波
李斐然,李 俊,蒋彦龙,谷 俊,詹宏波
(1.南京航空航天大学飞行器环境控制与生命保障工业和信息化部实验室,南京210016;2.苏州科技大学环境科学与工程学院,苏州215009;3.中国航空发动机集团航空发动机动力传输重点实验室,沈阳110015;4.南京机电液压工程研究中心航空机电系统综合航空科技重点实验室,南京211106)
板翅式换热器具有结构紧凑、体积小和经济性好的特点,广泛应用于航空航天、石油化工和汽车等领域。作为系统的主要部件,换热器出口平均温度测量是否准确,直接关系到系统的整体安全和稳定。
相比于传统的试验方法,仿真计算能够节省很多人力和时间成本,且工程算法无法考虑流量分配对传热造成的影响,厉彦忠等[1]以实验和计算流体力学(Computational fluid dynamics,CFD)仿真方法来模拟各类封头形式对流体分配特性的影响,指导提高流体进入换热器芯体的均匀性[2-3]。Zhang和Li[4]通过CFD 方法模拟了入口封头结构对于流量分配的影响,结果显示封头的不合理结构会造成流量分配不均。李焱等[5]通过CFD 方法模拟研究了两种换热器单层通道入口分配方式对单通道内气液流场分布的影响,研究表明流量的增大会导致气液分配不均匀度增高。吴静玮等[6]提出了一种多级导流封头,并通过CFD 模拟分析了对板翅式换热器通道内流量分配特性的影响, 研究表明流量分配均匀性相较于原始封头和最优的导流翼封头均有提高。曹学文等[7]采用MATLAB 和FLU-ENT 联合仿真方法分析板翅式换热器内部流量分配特性对换热器的影响,研究表明流量分配不均会造成热边不能冷却到理想温度等问题,造成换热效率下降。文献[8-9]使用可视化粒子图像测速法(Particle image velocimetry, PIV)方法研究板翅式换热器入口封头内部的流场分布特性,对封头体的整体改进提供了研究思路。李俊等[10-11]提出了机载交叉式多股流板翅式换热器数学模型,并通过VC++语言编制程序实现数值计算。
上述研究工作主要针对空分领域,对换热器封头研究集中于入口封头流量分配特性及结构优化,出口封头及后续管路的仿真模拟较少。在航空领域,预冷器从发动机引气,冷热边有很大温差,按照工程算法进行计算偏差较大,因此需要采用新的仿真方法。本文借鉴先前学者的数学模型,采用新的板翅式换热器联合仿真方法,研究换热器热边特性,分析大温差换热条件下出口封头温度场特性,得到后续管路的温度分布,并基于特定的换热器形式,结合热动力试验验证仿真计算方法。
1 联合仿真
1.1 联合仿真模型
板翅式换热器芯体内部通道尺寸小,结构复杂,如果对芯体翅片结构划分网格,会导致生成网格数量巨大,计算时间冗长,因此采用联合仿真方法,芯体部分使用基于VC++语言的编制程序进行计算,减小了网格数量,大大缩短了计算时间。
本文采用的联合仿真方法将板翅式换热器分为入口-换热器芯体-出口封头及后续管路3 个部分。入口管和入口封头部分对换热器整体进行网格划分,芯体仅考虑造成的压降影响,对芯体进行简化,得到流量分配情况;出口封头及后续管路部分,将芯体计算程序得到的结果通过UDF 编译作为边界条件进行仿真计算,最终得到出口封头及管路的流场和温度场。联合仿真过程如图1所示。

图1 联合仿真过程Fig.1 Joint simulation process
1.2 封头
在FLUENT 软件中建立封头模型,入口封头只进行流场计算,流场的Navier-Stokes (N-S)方程包括连续性方程和动量方程

式中,k 为紊动能;ε 为紊动耗散率;Gk为紊动能产生项;σ 为紊流普朗特数;μ 为气体动力黏度;C1ε,C2ε和Cμ为ε 方程常数。
因在大温差条件下换热器出口温度梯度很大,且机载预冷器介质为空气,因此密度变化不能忽视,应视为可压缩流动。出口封头仿真在之前基础上额外求解的能量方程,一般形式为
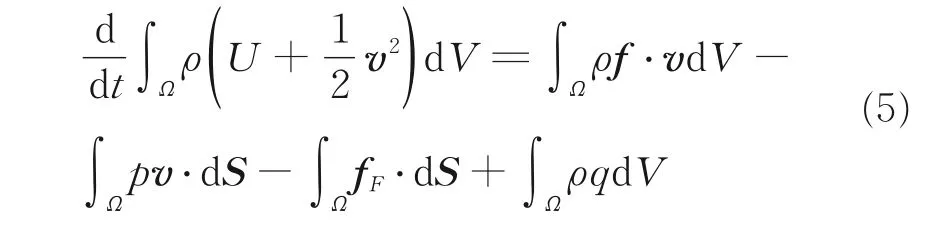
式中,左侧为体积Ω 中内能U 和动能之和,右侧依次 为 热 对 流 项∫Ωρf ⋅vdV-∫Ωpv ⋅dS、热 传 导 项-∫ΩfF⋅dS 和热辐射项∫ΩρqdV。
对于换热器计算,可忽略热辐射项,即

流量分配仿真还需考虑芯体背压对入口封头流量分配的影响,为了简化计算,芯体通道区域作为多孔介质进行处理,即将芯体通道简化为一个增加了阻力源的流体区域,其表达形式为

式中,Si为第i(x.y.z)方向上的动量方程源项;v 为速度值;Dij和Cij为指定矩阵D 与C 中的元素,式中右侧第1 项为粘性损失项,第2 项为惯性损失项。
对于多孔介质,式(7)可改写为

式中,α 为渗透率;C2为惯性阻力系数。
1.3 芯体
板翅式换热器芯体的物理模型如图2 所示,板翅式换热器任一通道流体温度变化受多种因素制约,翅片效率不为定值,因此需要对所有换热通道进行数值计算。为便于数值计算,作如下假设:(1)通道内流体沿通道高度方向温度相等;(2)忽略同一层流体横向热质交换以及流动方向热传导;(3)翅片和隔板厚度方向温度相同,且翅片根部温度等于隔板温度;(4)忽略各股流体压降对物性参数的影响;(5)换热器与外界环境之间无热量交换。

图2 板翅式换热器芯体结构Fig.2 Structure of plate-fin heat exchanger
基于上述假设,分别对流体、隔板以及翅片建立能量守恒方程。

式中,λ 表示换热器金属材质导热系数,F 表示流体间的相对流动方向(F 等于1 或-1);G 表示质量流速;cp表示流体定压比热容;H 表示翅片高度;f 表示翅片密度;δ 表示翅片厚度;T 表示流体温度;t 表示翅片温度;α 表示对流表面换热系数;x、l 分别表示流体沿流动方向、翅片高度方向笛卡尔坐标;下标i 表示通道编号。
根据上述微分方程,将换热器划分为W×L 个子单元换热器,对于式(9)中Ti(l)的一阶导数项,通过一阶中心差分离散为

对于流体与隔板、翅片的对流换热定性温度Ti(l),取子单元换热器流体进出口温度的算术平均值,其表达式为

综上,将各股流体的入口温度作为边界条件,可求得子单元换热器各股流体的出口温度,依次循环,采用逐行或逐列依次扫描的方式进行求解,可获得板翅式换热器各层流体的温度场。
2 试验验证
2.1 换热器热动力试验台
本文选择某型号预冷器进行试验,试验系统原理如图3 所示。热动力试验台采用独立空气源,两路空气管道在进入板翅式换热器试验件前配有加热电炉和调节阀。热边加热炉前、冷边加热炉后配备量程相同的质量流量计测量热边和冷边流量G1、G2,加热炉后试件前和试件热边出口后配备有压力变送器测量热边和冷边进口压力P1、P2及热边阻力ΔP,加热炉后试件前使用PT100 温度传感器(精度A 级)测量热边和冷边进口温度T1、T2,试件热边出口后使用铠装热电偶测量热边出口温度T3。试验系统实物图如图4 所示。
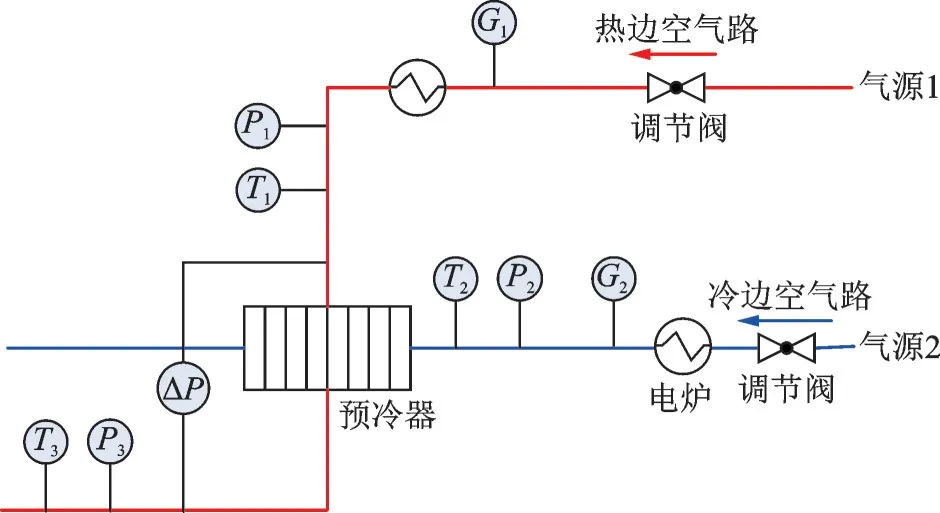
图3 热动力试验系统原理图Fig.3 Principle of thermodynamic test system

图4 热动力试验系统实物图Fig.4 Physical image of thermodynamic test system
试验测量仪器主要由质量流量计、压力变送器、压差变送器、温度传感器组成。试验仪器参数及准确度如表1 所示。
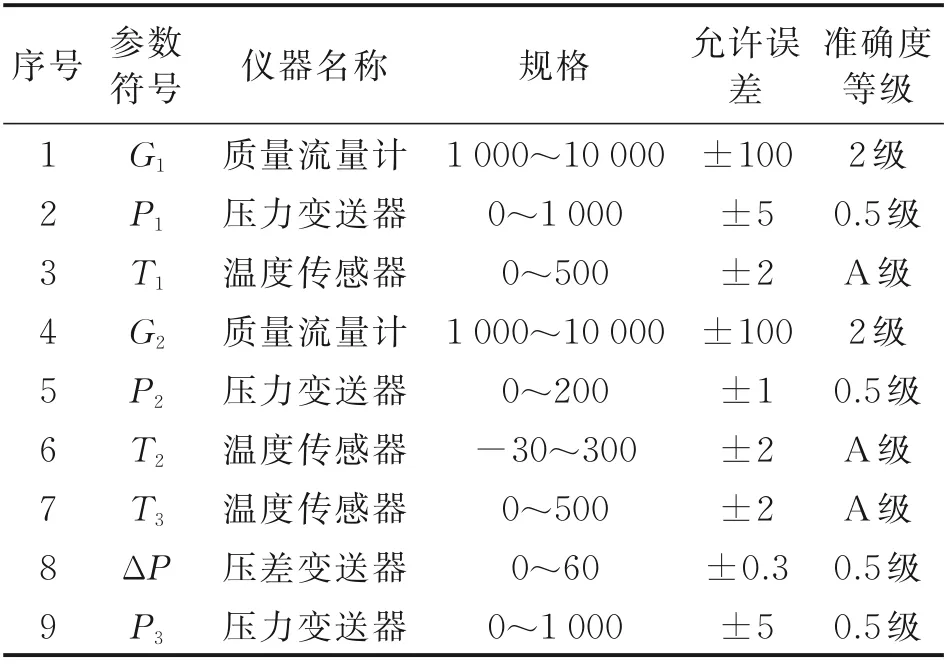
表1 实验仪器参数及准确度Table 1 Experimental instrument parameters and accu-racy
2.2 换热器芯体结构参数及数值计算设置
该板翅式换热器芯体结构参数如表2 所示。

表2 板翅式换热器芯体结构参数Table 2 Structure parameters of plate-fin heat exchang-er core
采用ICEM 软件对三维模型进行网格划分,采用结构网格划分方法对计算域生成网格。采用有限容积法离散控制方程组进行数值求解,速度与压力耦合采用同位网格上的压力耦合方程组的半隐式 方 法(Semi-implicit method for pressure linked equations,SIMPLE)算法,对流项采用二阶迎风格式,湍流控制方程采用标准k-ε 方程,离散后的控制方程采用非耦合隐式算法求解。
入口封头流量分配仿真只进行流场仿真,入口条件设置为mass-flow-inlet 边界,出口条件设置为outflow 边界,壁面设置为无速度滑移。出口封头仿真入口条件设置为mass-flow-inlet 边界,初始质量流量及温度使用用户定义函数(User-defined func-tions,UDF)对各通道进行初始化加载,出口条件设置为pressure-outlet 边界,壁面设置为无速度滑移,因为流动过程为可压缩流动,空气的物性参数需要独立设置,密度使用克拉伯龙方程进行推导,将密度视为关于温度的单值变化函数,根据工况条件进行拟合,黏度使用萨瑟兰(Sutherland)公式。求解过程中,当动量和连续性残差绝对值小于10-5,能量残差绝对值小于10-6,认为计算收敛。
以单一工况进行网格无关性检验,采用的网格数分别为48×104、107×104、240×104和283×104。计算得到的出口平均温度随网格数的变化如表3所示。可以认为网格数超过240×104时,计算结果受网格数影响很小。

表3 网格数量对出口温度影响Table 3 Influence of the number of grids on outlet temperature
2.3 试验结果对比及特性分析
2.3.1 模型验证
试验介质为空气,10 组试验热边进口压力为420 kPa,冷边进口压力为103.5 kPa。冷边进口流量最低为1 353 kg/h,最高为5 031 kg/h;进口温度最低为14.8 ℃,最高为20.6 ℃。热边进口流量最低为1 349 kg/h,最高为5 093 kg/h;进口温度最低为249 ℃,最高为401.9 ℃。10组试验的换热效率如表4所示,通过对比可以看出仿真换热效率与试验值基本相符,说明芯体计算程序的准确可行;仿真换热效率均略大于试验换热效率,说明芯体换热计算程序与实际换热之间存在一定差距,有进一步优化的空间。

表4 10 组试验换热效率Table 4 Heat transfer efficiency surface of ten sets of tests

图5 10 组试验平均温度及试验5 各测点对比Fig.5 Average temperature of ten sets of tests and the com-parison of test points in test 5
图5 为T3测温面的10 组试验平均温度及试验5 各测点温度对比图。从图5(a)可以看出,当出口平均温度较小(试验1~5)时,试验值与数值计算结果误差很小,结果非常接近。当出口平均温度较大(试验6~10)时,试验值与数值计算结果有一定误差,最大误差为6.4%。试验6~10 的误差大于试验1~5 的原因有以下两点:(1) 在平均温度较高的工况下,芯体换热计算程序与实际换热之间的误差增大;(2) T3测温面内温度梯度升高,铠装热电偶的安装位置对试验测值会产生影响。从图5(b)可知,试验5 中T3测温面内存在着一定的温度梯度,测点位置温度与数值计算结果基本一致。以上两图说明试验数值计算结果和试验数据表现出一致的变化规律,联合仿真方法准确可行。
为了评价热流体在出口管路内截面的温度分布情况,采用数理统计学中标准方差理论进行评估,量纲为一的温度分布不均匀度ST的计算公式为

由式(12)可以得出平均温度高于130 ℃(试验5~10)下T3测温面各点和仿真截面上的不均匀度,结果见表5。从表5 中数据可以看出,随着试验平均温度的升高,T3测温面的不均匀度逐渐增加,但试验8、9 的仿真不均匀度并没有大于试验7,比较试验参数可知,两组试验的冷热边流量很大且比值基本为1∶1,试验7 和10 均是热边流量远大于冷边流量,因此试验8、9 的不均匀度较小;试验的6 个测点所得到的不均匀度小于仿真数值计算结果,并且试验5 的平均温度最小,但试验不均匀度最大,二者说明测温点选取个数较少,结果不能完全反映该测温面的不均匀程度,存在一定偶然性。
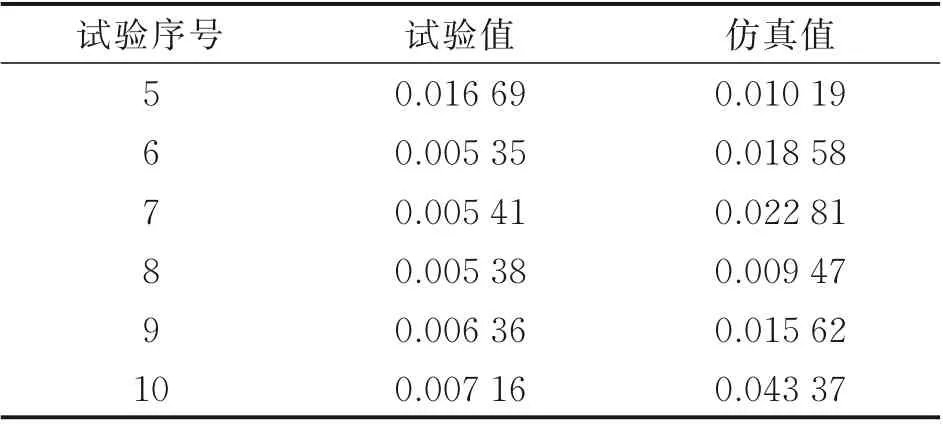
表5 6 组试验T3测温面不均匀度Table 5 Unevenness of T3 temperature measurement surface of six sets of tests
对比试验数据可以得到,仿真计算的误差为0.6%~6.4%,仿真计算的平均温度结果普遍低于试验结果,数值大小上存在偏差,这主要是受到芯体传热计算与实际换热之间误差影响。产生误差的另一个原因在于试验测温面只放置了6 个热电偶,数量较少,且测温面上存在温度梯度,安装过程中的深入距离及角度的偏差同样会对平均温度结果造成一定影响。
2.3.2 换热器热边特性分析
为了进一步探究换热器热边特性,以试验5 为例进行分析,通道内横向坐标轴正方向为冷边流动方向,热边空气流量为1 381 kg/h,温度为398.5 ℃,进入板翅式换热器入口封头,流场分布如图6(a)所示。最大流速为10.54 m/s,随着远离入口管位置流速逐渐减小,最小流速为3.07 m/s,且同时出现在通道14 两侧。换热器入口封头流量分配不均现象不仅发生在不同通道之间,同一通道内同样存在。
选取通道2,7,14 进行对比,温度分布如图6(b)所示。可以看到,在同一通道内,热边空气随着流动距离的增加,温度逐渐降低。同时观察横向温度梯度可以看出,温度变化与距冷边入口距离(通道内横坐标)接近线性分布。另外,定义T(i,j)为热边通道内任意点(i,j)的温度,在靠近冷边入口的区域,3 通道相同位置温度逐渐升高,即T2(i,j)>T7(i,j) >T14(i,j);在 远 离 冷 边 入 口 的区域,T2(i,j) <T7(i,j) <T14(i,j)。
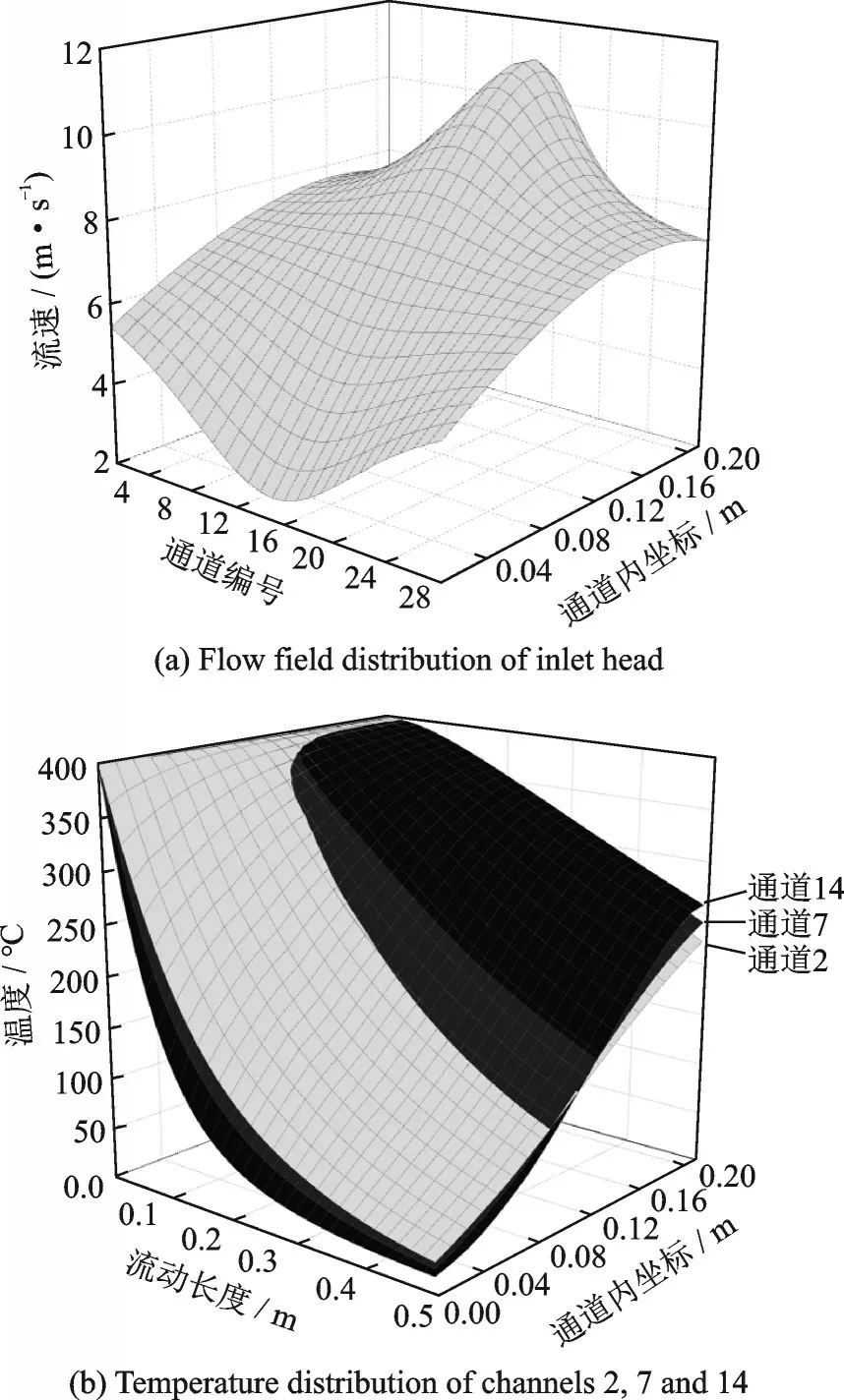
图6 入口封头流场分布和3 通道内温度分布Fig.6 Flow field distribution of inlet head and temperature distribution in three channels
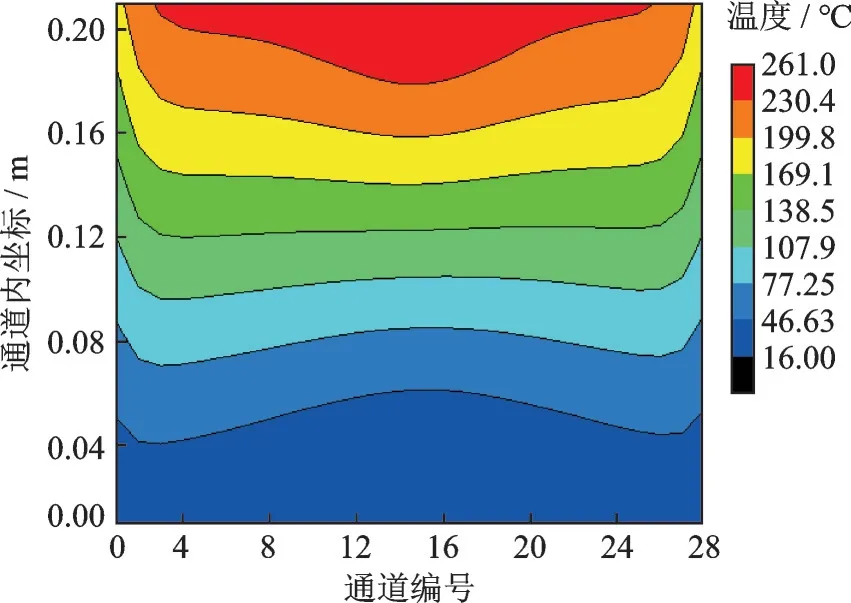
图7 芯体出口温度分布Fig.7 Temperature distribution at the core outlet
图7 为芯体出口温度分布情况,由图7 可以看出热边的质量流量分布与出口温度分布大致呈相同的变化规律,即高流量的出口温度高,低流量的出口温度低,分布具有不均匀性。值得注意的是在通道内横向方向温度分布变化较大,这是因为冷边空气为14.8 ℃的均匀流,与热边温差很大,热边与冷边首先接触的区域是远离入口管一侧,随着冷边空气逐渐推进,温度逐渐升高,换热能力下降,因此相较于纵向而言,横向存在较大温差。在流量分配不均和冷边流动方向的叠加影响下,形成了如图8所示的出口温度分布形式。
定义x 为距出口管与封头接口根部的距离,得到换热器出口管路各截面温度分布,如图8 所示。可以看出,刚进入出口管路时温度分布是非常不均匀的,随着流动距离的增加,温度梯度逐渐减小,温度场逐渐均匀。
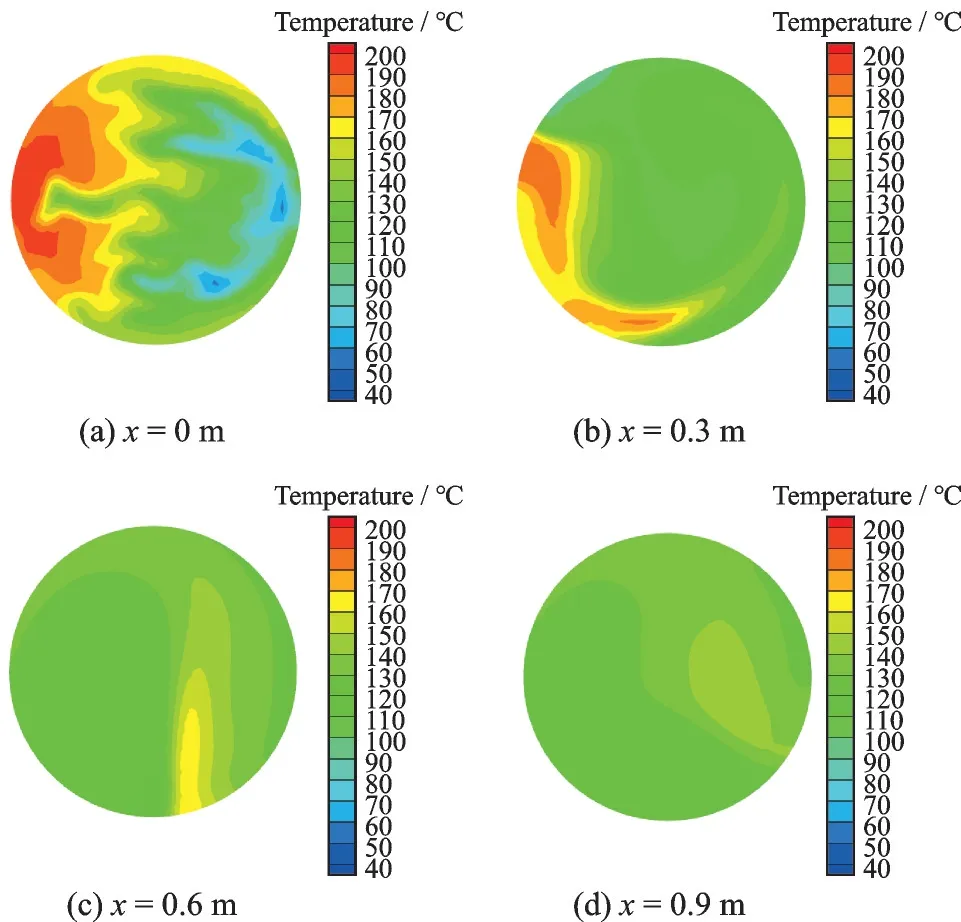
图8 出口管路温度分布Fig.8 Temperature distribution of outlet pipe
3 结 论
(1)本文将联合仿真方法应用于板翅式换热器仿真计算,大大提高了计算效率,对于研究大温差换热条件下航空预冷器温度场特性有现实意义。
(2)在给定换热器结构形式下进行了试验对比验证,误差为0.6%~6.4%,误差较小,在工程化应用上具有参考意义。
(3)传统试验方法采用有限个温度测点进行测量,无法完整反映测温面的温度分布情况,温度场仿真具有必要性。
(4)在同一通道内,热边空气随着流动距离的增加,温度逐渐降低;观察横向温度梯度可以看出,温度变化与距冷边入口距离(通道内横坐标)接近线性分布。
(5)热边质量流量和出口温度分布大致呈相同的变化规律,即高流量的出口温度高,低流量的出口温度低,分布具有不均匀性,并且出口温度分布受到流量分配不均和冷边流动方向的叠加影响。
