基于多组并行深度Q网络的连续空间追逃博弈算法
2021-05-06刘冰雁叶雄兵岳智宏董献洲张其扬
刘冰雁, 叶雄兵, 岳智宏, 董献洲, 张其扬
(1.军事科学院, 北京 100091; 2.32032部队, 北京 100094)
0 引言
以追捕者视角看待的追逃博弈(PEG)问题[1],是在仅知自身状态和逃逸者当前有限状态、未知逃逸者未来行为策略的条件下采取最优行为,并最终完成追捕任务的一个动态博弈过程。该问题是最优控制与动态博弈的深度融合,现已在战车追捕[2]、战斗机格斗[3]、导弹拦截[4]以及航天器交会[5]等军事应用场景中被重点关注。
PEG问题中的逃逸者,除了在一个连续且动态变化的空间环境中活动外,还具有典型的非合作性,即有信息层面不沟通、机动行为不配合、先验知识不完备等特性[5]。针对此类军事场景中常出现的双方连续动态冲突、对抗博弈问题,可通过微分对策[6-7]进行数学描述。这类追捕- 逃逸微分博弈是微分对策的一种应用,最初由Isaacs[1]提出,近年被广泛运用到诸多领域。例如,文献[8-9]根据机器人追捕问题的具体情况,通过分析追逃双方的不同状态及形势,建立了追捕者与逃逸者的微分博弈描述式。文献[10]将高速机动目标拦截末制导过程抽象为以视线角速率和燃料消耗为性能指标的零和微分博弈问题,设计了一种微分对策制导律,以表述对目标的拦截策略。文献[11-12]在主动防御飞行器制导问题研究中,运用微分对策理论对对抗双方的制导律进行了描述与设计。文献[13]在三维空间中多智能体参与的PEG问题研究中,利用微分对策设计了防御器和逃逸器的最优控制策略。文献[14]为获得追逃双方在对策条件下的最优策略,运用微分博弈对航天器的整个追逃过程进行了数学描述。但在利用微分对策描述PEG问题过程中,由于会面临多目标求解、方程复杂度以及约束非线性等诸多难题,导致其求解过程一直较为棘手[15]。
当前,强化学习技术[16]在有效结合深度学习[17]后得到了进一步发展,为微分对策问题提供了更好的解决方案,并受到各领域广泛关注[18-19]。例如,针对实时对抗微分对策问题,Deepmind科研团队利用深度学习展现了强大的信息处理和决策能力,之后又结合强化学习技术以提升实时对抗和动态博弈能力,使其自主对抗决策能力接近人智水平[20]。文献[21]阐述了军事智能博弈对抗的发展需求和概念内涵,分析了基于强化学习的博弈对抗特点,展望了智能博弈对抗技术的发展方向。文献[22]在交通网络信号控制领域研究中,融入博弈论的混合策略纳什均衡概念,改进IA-MARL的决策过程,提出了一种考虑博弈的多智能体强化学习框架,有效降低了车辆在不饱和且交通需求不均衡和波动的城市路网中的单位行程时间和单位车均延误。文献[23]针对无人机通信网络中的干扰对抗问题,考虑无人机网络节点的动态特性,将干扰器视为分层博弈领导者无人机用户视为分层博弈跟随者,提出一种基于分层博弈的自适应频谱接入优化机制,智能地调整信道选择从而获得了良好的吞吐量性能。因此,基于深度强化学习的技术性突破,对解决高动态、不确定以及复杂环境下的微分对策问题,将具有重要的理论意义和应用价值[24-27]。
在空中格斗、导弹拦截、战车追击以及空间非合作目标交会等军事对抗中,追捕者试图在最短时间内追上逃逸者,而逃逸者则试图尽可能避开追捕者的现实问题,是典型的双方对抗博弈问题。本文在运用强化学习解决此类PEG问题过程中,针对传统Q-learning应对连续空间存在维数灾难问题,构建了Takagi-Sugeno-Kang(TSK)模糊推理模型表征连续空间行为;针对离散动作集自学复杂且耗时问题,设计了多组并行的深度Q网络(DQN)算法,从而达成以较短学习时间、在连续空间快速完成追捕任务的研究目标。
1 连续空间的TSK模糊推理模型
PEG问题通常出现在连续空间,但传统强化学习可能会由于其状态连续性、多维并存而存在维数灾难问题[28]。为有效避免这一问题,本文依据“模糊推理是一种可以任何精度逼近任意非线性函数的万能逼近器”[29]的结论,通过构建一个TSK模糊推理模型来表征连续空间,并将其作为强化学习中的一部分。
通过零阶TSK模糊推理模型[30],结合隶属函数[31]表征连续状态行为空间,经过IF-THEN规则获得模糊集到输出连续线性函数之间的模糊映射关系[32]为
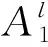
(1)
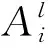
对于模糊模型的输出,可利用加权平均去模糊化技术将模糊量转换成精确量[34]:
(2)
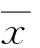
(3)
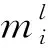
图1所示为输入量为2、隶属函数个数为3的TSK模糊推理模型。推广到一般情况,假设以n个连续空间行为变量xi为输入。对每个xi通过y个隶属函数,再经过去模糊处理后输出精确值U.
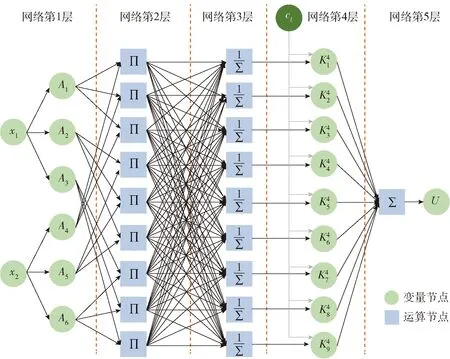
图1 TSK模糊推理模型Fig.1 TSK fuzzy inference model
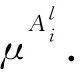
第2层网络中,采取直积推理[35],即分别在L(L=yn)个运算节点对各隶属度进行交叉相乘运算:
(4)
第3层网络中,进行加权平均去模糊化处理,归一隶属度为
(5)
(6)
第5层网络中,累计各节点,便可实现(2)式所示的去模糊化效果:
(7)
2 基于多组并行DQN的PEG
强化学习直接运用于TSK模糊推理模型,会面临行为数量与映射规则的组合增长问题,将大大削弱离散化处理后的行为控制决策能力。为此,本文构建多组、并行的DQN网络架构,设计PEG强化学习算法,提出追捕者与逃逸者的博弈交互训练步骤,在未知逃逸策略、行为动作的条件下,实现最优追捕行为的自主生成。
2.1 多组并行DQN网络架构
连续状态空间和行为空间,经过TSK模糊推理模型处理,依L条规则根据(5)式计算,获得L项归一化直积推理值。其间,构建多组并行的DQN网络架构,为基于TSK模糊推理预处理的追逃微分策略问题生成全局连续行为。
由此,依据TSK模糊推理模型中的L条规则,建立L组DQN网络,对PEG策略进行自主学习。多组并行DQN网络,是在单个神经网络基础上增加了多个并行神经网络。与单组神经网络[36]类似,并行神经网络在与环境的不断交互中自主学习并提升行为决策能力,通过在网络中加入博弈和反馈机制,使多组并行DQN网络具有更强的自主性、灵活性和协调性等特点,具备更强的学习、推理和自组织能力。
多组并行DQN基本架构如图2所示。其中,与L条IF-THEN模糊规则相对应的离散动作集a={a1,a2,…,aL},经过多组并行的神经网络计算,获得离散动作的状态行为函数(简称为q函数),再经过PEG强化学习算法以及加权平均去模糊处理,便可获得该状态下的输出行为U.
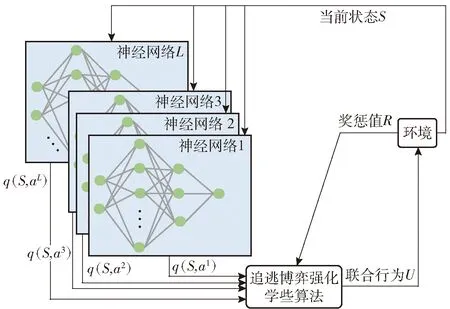
图2 多组并行DQN基本架构Fig.2 Basic framework of multi-group DQN
2.2 PEG强化学习算法
为运用多组并行DQN架构解决连续空间PEG问题,需要对模糊规则稍作调整,用al替换(1)式中的cl. 在运用加权平均去模糊化技术之前,依据输入量为n、隶属函数个数为y的TSK模糊推理模型,进行L(L=yn)条IF-THEN模糊规则映射:
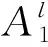
(8)
式中:al为追捕者离散动作集a中对应于规则l的动作。
为了有效解决强化学习中的探索与利用问题,即持续使用当前最优策略保持高回报的同时,敢于尝试一些新的行为以求更大地奖励,对行为al采取ε-greedy贪婪策略[25]。该策略定义追捕者以ε的概率在动作集中随机选取,以1-ε的概率选择一个最优动作。
(9)
式中:q(S,al)为规则和追捕者动作al∈a下的关联q函数。
根据(2)式,t时刻追捕者所采取的全局连续行为可表示为
(10)
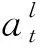
(11)
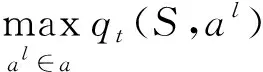
为了弥补DQN算法存在的奖励偏见问题,本文提出一种竞争网络取代经典算法中的单输出网络模型,以提升神经网络训练效果,加快收敛速度。将q函数的神经网络全连接层分解为一个状态函数vt(S)和一个优势函数ot(S,al),再通过全连接合并,有
qt(S,al)=vt(S)+ot(S,al).
(12)
利用优势函数期望值为0这一特性[37],用优势函数ot(S,al)减去当前状态下所有动作优势函数的均值,以控制优势函数的期望,进而(12)式修改为
(13)
DQN架构中,在奖惩值的牵引下为实现反馈自主学习,定义了时间差分误差函数:
(14)
式中:γ为折扣因子,γ∈[0,1];Rt+1为t+1时刻可获得的奖惩值。
通过神经网络迭代,更新q函数,有
(15)
式中:η为强化学习速率。
2.3 PEG交互过程
在追捕者与逃逸者的PEG交互过程中,追捕者当前行为的确定需要TSK模糊推理模型中离散动作集a={a1,a2,…,aL}的参与。运用多组并行DQN架构,可实现离散动作al的并行自主学习,在获得最优动作的同时提升运行时效。与此同时,多组神经网络并行部署,极大提升了离散动作的独立学习能力,增强了算法对环境探索的能力。
为使追捕者获得高效的追击行为策略,限定一次回合中最大时间步个数为M. 同时,为真实反映追捕者与逃逸者的PEG过程,随机初始化逃逸者初始位置、状态以及逃逸策略。在多次训练中,1轮PEG交互过程如图3所示。
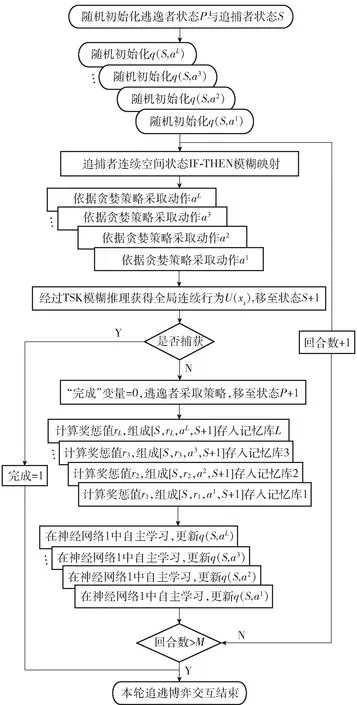
图3 PEG交互流程图Fig.3 Flow chart of pursuit-evasion game interaction
具体交互训练步骤如下:
步骤1随机初始化逃逸者位置状态P,设定逃逸者行为方式与逃逸策略;初始化追捕者位置状态S,定义追捕者追捕方式及行为边界条件;初始化系统变量“回合数”=0、“完成”=0.
步骤2根据追捕者位置状态S定义TSK模糊推理模型输入量n,设定隶属函数y. 依据模糊规则数,定义L(L=yn)组DQN网络,并对各网络的q函数进行随机初始化。
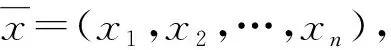
步骤4分别在与第l={1,2,…,L}条规则所对应的DQN网络中,根据(9)式选取动作al(l=1,2,…,L)。
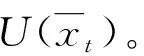
步骤6计算追捕者与逃逸者的欧氏距离,判断是否满足捕获条件。若满足,则令变量“完成”=1并转步骤11;若不满足,则执行步骤7.
步骤7令变量“完成”=0,依据策略逃逸者选择对自身最佳的行动方向,并移至下一状态P+1.

步骤9各组DQN网络中,依据(12)式~(15)式,以回报值rl为牵引,采取一定的学习率η,更新q(S,al)函数。
步骤10判断变量“回合数”是否大于最大行动步数M. 若“回合数”>M,则转步骤11;否则,“回合数”数量加1并转步骤3.
步骤11结束本轮PEG交互过程。
3 仿真分析
以四轮智能战车PEG问题为例设计仿真环境与运动模型,运用本文算法进行仿真实验,并与其他算法结果相比对,以验证本论文算法的有效性。
3.1 PEG仿真环境
PEG过程中,追捕者试图在最短时间内追上逃逸者,而逃逸者则试图尽可能避开追捕者。为了使仿真结果尽可能反映真实情况,需要提前构建仿真环境以及追捕者与逃逸者的运动模型。
假设整个追逃环境是无障碍的,追捕者与逃逸者均不知道对方下一步的行为选择,二者均可根据当前状态采取对自身最有利的行为,只有当逃逸者处于追捕者捕获范围或者“回合数”达到最大时间步M,本轮博弈交互过程结束。
如图4所示,以四轮智能战车PEG问题[39]为例,构建追捕者p与逃逸者e. 图4中,xp、yp为追捕者当前的笛卡尔坐标;xe、ye为逃逸者当前的笛卡尔坐标;vp、ve分别为追捕者与逃逸者速度,且定义追捕者快于逃逸者;θp、θe分别为追捕者与逃逸者的运动方向;Lp、Le分别为追捕者与逃逸者的轴距。

图4 追捕者和逃逸者的运动模型Fig.4 Motion model of pursuer and runaway
设追捕者和逃逸者的运动模型分别为
(16)
(17)
式中:up与ue分别为追捕者与逃逸者采取的转向角,up∈[-upmax,upmax]、ue∈[-uemax,uemax],upmax、uemax分别为追捕者与逃逸者的最大转向角;设定追捕者机动性能差于逃逸者,即upmax 由此,追捕者p和逃逸者e之间的角度差φ为 (18) (19) 式中:φ′为上一状态的角度差;T为采样时间。 追捕者p和逃逸者e之间的欧氏距离d为 (20) 在PEG过程中,追捕者p的目标是在最短时间内追上逃逸者e;而逃逸者e的目标是使得追捕时间最大化并避免被追上。只有当逃逸者e位于追捕者p捕获半径l内,即d≤l时,追捕任务才算完成。 追捕者p采取的策略是使得与逃逸者e之间的角度差φ趋于0,由此将多组并行DQN架构中的回报函数定义为 rl=2e-φ2-1, ∀l∈[1,L], (21) 追捕者p在连续空间可采取如下行为: (22) 逃逸者e选取对其最有利的逃逸策略,且不以追捕者p的意志为转移。借鉴文献[40-41]结论,逃逸者e将采用以下两种策略使得与追捕者p之间的距离最大化: 1)若二者之间欧氏距离d大于特定距离D,则逃逸者e将采取如下行为: (23) 2)若二者之间欧氏距离d小于特定距离D,则逃逸者e则将采取更高机动性的行为,即 ue=θp-θe+π. (24) 仿真实验在1.6 GHz、1.8 GHz双核CPU、8G RAM计算硬件上,运用PyCharm仿真编译环境进行。设定1轮episode中时间步个数M=360,采样时间T=0.1 s. 设定追捕者p的初始位置(xp,yp)=(0 m,0 m),初始方向θp=0°,恒定追捕速度vp=1 m/s,捕获半径l=0.1 m,轴距Lp=0.3 m,转向角范围up∈[-0.5°,0.5°]。随机初始化逃逸者位置(xe,ye),初始方向θe=0°,恒定逃逸速度ve=0.5 m/s,逃逸策略中特定距离D=3 m,轴距Le=0.3 m,转向角ue∈[-1°,1°]。多组并行DQN架构中,采用的神经网络层数为5,隐藏层神经元个数为10,激活函数为sigmoid,探索率ε=0.3,折扣因子γ=0.9,学习速率η=0.3. 运用本文所提算法进行仿真实验,与Q-learning算法[42]、基于资格迹的强化学习算法[33]以及基于奖励的遗传算法[43]实验结果进行比对。各算法在经过100次自主学习后,均能完成追捕任务,捕获时间和训练时间如表1所示。其中,Q-learning算法由于需要链式存储多个特征向量以及同时迭代更新多张Q表,导致其自主学习耗时较长;基于资格迹的强化学习算法将时序差分法和蒙特卡洛法相统一,只需要追踪一个迹向量,不再需要存储多个特征向量,大大缩减了自主学习时间,但其短期记忆特性延长了实际追捕时间;基于奖励的遗传算法,虽具有较高的实际应用性能,但却以更长的自主训练时耗为代价[43];本文所提算法,在充分发挥强化学习算法自主寻优优势的同时,运用多组神经网络对进行并行训练,大大缩减了自主学习耗时,并能确保在较短时间内完成追捕任务。 表1 不同算法完成捕获任务的耗时Tab.1 Elapsed time of different algorithms to complete the capture task s 图5展示了当逃逸者初始位置为(5 m,5 m)时运用本文所提算法,分别经过自主学习0次、50次和100次后的PEG过程。图6和图7分别展现了3种情况下PEG过程中,追捕者与逃逸者之间距离及角度差的空间变化情况。其中,如图5(a)所示,当算法不经学习直接应用于该PEG问题,追捕者虽以角度差趋于零为行动目标,但由于其q函数随机生成,且没有任何先验知识,导致角度差上下来回浮动,与逃逸者距离却越来越大,不能完成任务。如图5(b)所示,当算法经过50次自主学习后,追捕者能够朝着追捕者方向逼近,途中逃逸者采取更为灵活的规避策略,致使与追捕者角度差陡增,追捕者在紧急转向后顺利完成追捕任务。如图5(c)所示,当算法获得更多的学习次数后,能够更好地处理逃逸者规避行为,自主选取更为有利的行动方向,从而大大提升了任务完成效果。 图6 追捕者与逃逸者之间的距离变化Fig.6 Distance between pursuer and runaway 图7 追捕者与逃逸者之间的角度差变化Fig.7 Angle difference between pursuer and runaway 本文提出一种自主学习时间少、问题应用耗时短的PEG算法,实现了追捕者在连续空间最优追捕行为的自主生成。通过构建TSK模糊推理模型以表征连续行为空间,构建多组并行的DQN架构,设计基于DQN的PEG算法,提出追捕者与逃逸者在连续空间博弈交互的训练步骤,从而有效地避免了传统强化学习应对连续空间所可能存在的维数灾难不足,实现了最优追捕行为的自主生成,有效解决了离散动作集自学习复杂且耗时的问题。连续空间PEG方法不仅能够完成连续空间PEG任务,还能随着学习次数增加不断提升问题处理能力,满足动态实时博弈需求,对于解决其他领域的PEG问题同样具有借鉴意义。

3.2 算例仿真

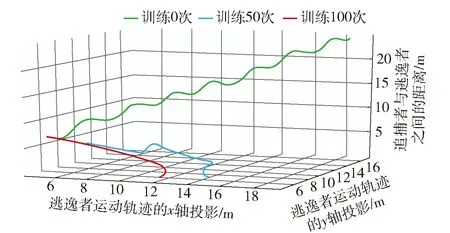
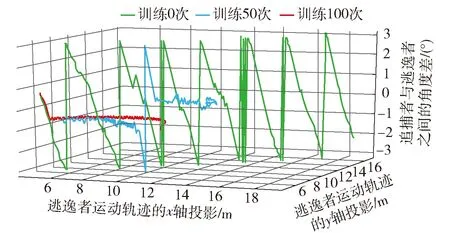
4 结论
