结构可靠性分析的自适应共轭非线性近似方法

邱继伟， 罗海胜

(中国兵器工业标准化研究所， 北京 100089)

0 引言

可靠性作为通用质量特性的核心，长久以来制约着我国兵器装备及其相关技术向更高层次推进，致使我国目前的装备质量水平相对于欧美军事强国有较大差距。提升兵器装备的通用质量特性，必须将强化其可靠性水平作为重要目标，因此系统、深入地开展可靠性相关工作仍将是当前及未来相当长时期内我国兵器装备领域研究的重点，也是提升装备通用质量特性的关键。

兵器装备是典型的机电产品，机械产品占有较大比重。因此，针对机械类产品和零部件进行的可靠性分析、设计等工作对提升装备整体通用质量特性具有重要作用。机械产品可靠性分析的主要目标是计算其在规定工况下的失效概率Pf[1]：

(1)

式中：X为基本随机变量所组成的向量，X=[x1,x2,…,xn]T；g(X)为产品可靠性极限状态函数，g(X)≤0表示产品处于不可靠状态；fX(x1,x2,…,xn)为随机向量X各分量的联合概率密度函数；上述及下文中，n∈N.

实际工程中，基本随机变量的联合概率密度函数fX(x1,x2,…,xn)难以得到，同时，(1)式中的多重积分也难以求解。通常情况下，可采用两类方法进行机械产品失效概率的近似计算，即解析方法和数值模拟方法。解析方法中以1阶可靠性方法[2-4](FORM)和2阶可靠性方法[5-6](SORM)最为实用，两类方法在本质上都是利用梯度和曲率等几何条件，对极限状态函数进行局部近似，进而求得所需的可靠度系数。数值模拟方法以蒙特卡洛仿真[7-8](MCS)为基础，通过抽样方法对(1)式中的多重积分进行近似求解；对于无法获得显式极限状态函数的可靠性分析问题，可通过构建代理模型[9-13]对产品的真实极限状态函数进行近似，进而采用数值模拟方法计算其失效概率。

目前，求解结构可靠性分析问题解析方法均不同程度地以FORM中经典的Hasofer-Lind and Rackwitz-Fiesslen(HL-RF)方法[14]或有限步长法[15](FSLM)为基础，利用迭代设计点的极限状态函数值及其梯度等单点局部信息，近似求解响应的可靠度系数。Santosh等[16]基于Armijo准则，通过设计有限迭代步长对HL-RF算法进行了改进。Yang[17]利用稳态变换方法(STM)，并基于混沌反馈控制算法改进了经典FORM算法的稳定性。虽然FSLM、STM和方向STM[18]等方法相对于HL-RF方法具有较高的计算稳定性，但迭代步长和控制参数的选择会显著影响上述3类方法的计算效率[19]。同时，一些改进的HL-RF方法，例如松弛HL-RF方法[20]、混合松弛HL-RF方法[20]、混沌共轭稳定性变换方法[21]等，虽然可以改善计算过程的稳定性，然而线性或弱非线性问题的求解效率则远远低于HL-RF方法。

基于经典FORM进行结构可靠性分析时，关键在于对非线性问题求解的高效性及稳定性。前述方法在迭代求解可靠度系数时，仅利用了单一迭代设计点的极限状态函数值与梯度值等局部信息，极易导致计算的不稳定性。因此，本文在两点自适应非线性近似(TANA)方法的基础上，通过构建共轭搜索方向，并利用当前迭代设计点和以往若干步迭代设计点的信息(包括精确极限状态函数值及梯度值)，提出一种自适应共轭非线性近似(SACS-TANA)方法，在迭代过程中自动调整近似模型的非线性指数和搜索方向，提高对非线性可靠性问题求解的效率和稳定性。最后，通过3个案例验证了所提方法的适用性。

1 FORM概述

应用FORM进行结构可靠性分析的最终目标是根据其极限状态函数，在标准正态随机变量所张成的空间(以下简称标准空间)中寻找结构的最可能失效点(MPP)[22]，即极限状态函数所表示的曲面上与标准空间原点距离最近的点，也称为设计点。因此MPP的搜索问题可以表述为如下最优化问题[19]：

(2)

式中：β表示结构极限状态曲面上的点与标准空间原点的欧式距离；g(P)=0为标准空间中的极限状态曲面方程；P表示随机变量X在标准正态空间内的映射，通常需要由物理随机空间变换到标准正态空间。该优化问题的最优解用P*表示，其意义为MPP点。MPP点对应可靠度系数即为β*，则β*=‖(P*)TP*‖。

针对上述最优化问题，Hasofer等[23]首先提出了HL方法，采用迭代公式(3)式求得标准空间中的设计点P*：

(3)

HL方法以及在此基础上的各种改进迭代算法(如HL-RF方法、STM、FSLM等)对于极限状态函数进行了基于泰勒技术展开的线性近似，且仅利用了标准空间中单点处的局部信息，包括其极限状态函数值与梯度向量。然而，当极限状态函数的非线性程度较高时，基于单点函数值及梯度值的迭代算法极易出现求解结果振荡或陷入局部最优，迭代过程难以继续，导致结构可靠度计算结果失真甚至错误。

2 基于自适应共轭搜索方向的TANA方法

2.1 TANA方法基本原理

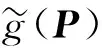
TANA模型由Wang等[24]提出，在对(2)式表示的最优化问题进行迭代计算的过程中，采用当前迭代点和上一迭代点的函数值和梯度信息构建近似极限状态函数，并利用自适应干涉变量的泰勒级数展开式进行近似。构建TANA模型的主要步骤如下：

1) 在原始随机变量所张成的空间(以下简称原始空间)中，构建真实极限状态曲面的近似函数为

(4)

2) 利用前次迭代点的信息计算(4)式中的自适应非线性指数ρ为

(5)

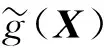
(6)

式中：μxi和σxi分别为随机变量xi的均值与标准差。

由此可以看出，TANA方法在构建近似极限状态函数的过程中，利用了前次迭代设计点的极限状态函数值信息，通过自动调整ρ值，获得最优的近似。TANA方法所构建的模型对于非线性程度较高的极限状态函数具有较好的局部近似能力[22]。

2.2 结构可靠度计算的SACS-TANA方法

经典FORM(例如HL方法、HL-RF方法、有限步长法等)在计算结构可靠度的过程中，仅采用了当前迭代设计点的梯度信息，对于非线性程度较高的结构极限状态函数，(3)式中的γk向量在迭代计算过程中很可能与之前迭代设计点处的梯度向量共线，进而造成迭代过程具有周期性，计算结果难以收敛于真实的设计点。因此，本文在基于TANA模型的基础上，借鉴FR共轭方法[25](FRCM)，提出一种自适应共轭搜索非线性近似计算方法，利用当前迭代设计点以及以往两步迭代设计点的极限状态函数值和梯度信息，在计算过程中对迭代搜索方向进行自适应调整，避免求解过程的周期性，提高计算结果的稳定性和精确性。

本文所提出的SACS-TANA方法具体步骤如下：

步骤1基本随机变量的等效正态化处理。等效正态化处理后基本随机变量所组成的向量表示为X=[x1,x2,…,xn]T.

步骤2进行第1次迭代过程。选择等效正态化后的各随机变量均值点作为初始迭代设计点，利用1阶泰勒展开构建初值点处的近似极限状态函数，并计算初值点处的极限状态函数值及梯度值。

步骤3采用均值点法求解初始可靠度指标β1及相应的方向余弦γ1=[γ11,γ12,…,γ1n]T，并计算新的设计点X1=[x1,1,x1,2,…,x1,n]：

x1,i=μxi+β1σxiγ1i，

(7)

式中：[μx1,μx2,…,μxn]T=μ和[σx1,σx2,…,σxn]T=σ分别为随机向量X所对应的均值向量和标准差向量。

步骤4重复步骤2、步骤3，得出新的迭代设计点Xk、Xk+1(k≥2)，并计算相应的极限状态函数值及梯度值。

步骤5根据TANA方法的(4)式，在原始空间中利用设计点X2、X3的极限状态函数值及梯度值构建近似极限状态函数，并基于(5)式计算自适应非线性指数ρ.

步骤6利用(6)式将原始空间中的近似极限状态函数变换到标准空间中，用上标c表示标准空间。

步骤7在标准空间中，构建如下共轭搜索方向：

(8)

式中：ηk为共轭搜索方向向量，

(9)

系数ξk和θk分别定义如下：

(10)

(11)

步骤8计算得到新的设计点。根据(12)式迭代计算得出标准空间中新的设计点Pk+1=[pk+1,1,pk+1,2,…,pk+1,n]：

(12)

步骤9将标准空间中的设计点变换到原始空间中：

xk+1,i=μxi+σxipk+1,i.

(13)

步骤11得出结构可靠度指标β=βk+1=‖Pk+1‖2.

3 案例分析

3.1 数值案例

3.1.1 数值案例1

考虑非线性极限状态函数为

(14)

式中：随机变量x1及x2服从相同的正态分布，二者的均值分别为μx1=10、μx2=9.9，标准差为σx1=σx2=5. 采用HL-RF方法、FR共轭方法、TANA方法与本文所提SACS-TANA方法计算上述极限状态函数所对应的可靠度系数，在给定误差限为0.001的前提下，与1 000 000次MCS结果[22]进行对比，如表1所示。

由表1可以看出，经典FORM中的HL-RF方法在迭代21次后结果出现振荡，且计算结果并未收敛至准确的可靠度系数；而本文所提出的SACS-TANA方法与未采用共轭搜索方向的经典TANA方法，经过3次迭代计算即可收敛至准确结果；基于共轭搜索方向的FRCM则经过7次迭代收敛得到准确的可靠度系数。算例表明，采用共轭搜索方向且同时考虑近似模型本身非线性特征的SACS-TANA方法具有较高的精度及计算效率。

3.1.2 数值案例2

考虑如下高维极限状态函数：

(15)

式中：随机变量xi,i=1,2,…，n独立同分布，服从均值为1、标准差σ=0.2的对数正态分布。本案例中，取n=100，采用1 000 000次MCS分析，得出上述极限状态函数所对应的可靠度系数β=2.923 6[12](对应的失效概率为Pf=1.73×10-3)。在规定迭代误差为0.001的基础上，利用HL-RF方法、FRC方法、TANA方法与本文所提出的SACS-TANA方法近似计算上述极限状态函数所对应的可靠度系数，并与MCS分析结果进行对比，如表2所示。

表1 数值案例1可靠度系数迭代过程对比Tab.1 Comparative results of different methods for reliability index iteration of numerical example 1

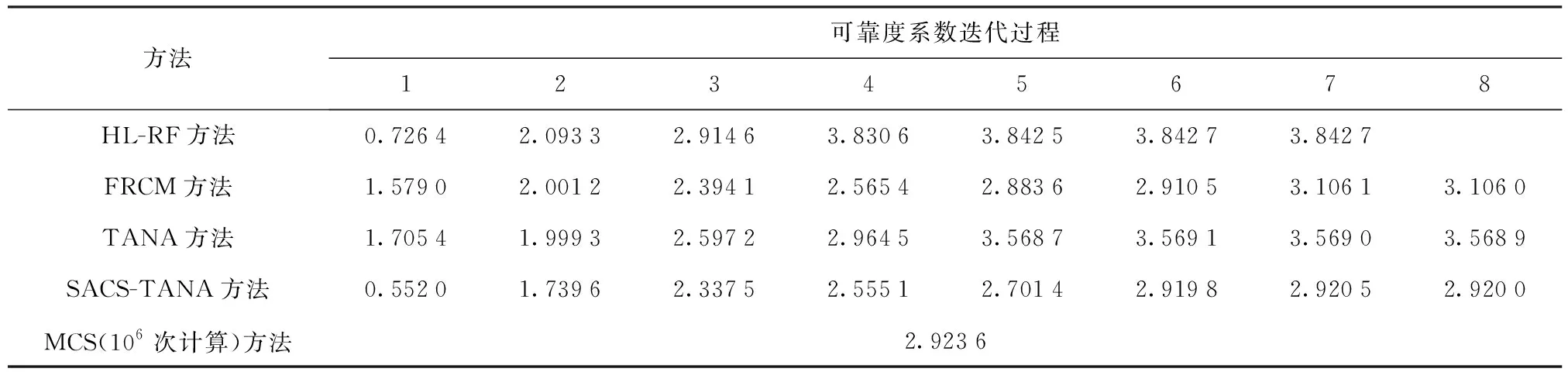
表2 数值案例2可靠度系数迭代过程对比Tab.2 Comparative results of different methods for reliability index iteration of numerical example 2

由表2可以看出：经典FORM中的HL-RF方法在迭代5次后，计算结果收敛至β=3.842 7(相对误差为31.44%)；基于共轭搜索方向的FRCM，经过7次迭代计算后结果收敛至β=3.106 1(相对误差为6.24%)；未采用共轭搜索方向的经典TANA方法，经过5次迭代计算后，结果收敛至β=3.569 0(相对误差为22.08%)；而本文所提出的SACS-TANA方法，经过6次迭代计算即可收敛至准确结果β=2.920 0(相对误差为0.12%)。综合数值案例1、案例2的计算结果，表明本文所提出的SACS-TANA方法对于非线性及高维极限状态函数的可靠性指标求解均具有较好的适用性。

3.2 结构可靠性分析案例

某锥体结构的尺寸及其受载情况如图1所示，其中，M和p分别为其所受的弯矩(N·m)和轴向压力(N)，d为锥体壁厚(m)，α为倾斜角(rad)，ri为锥体内径(m)；ro为锥体外径(m)。由弹塑性力学理论可知，锥体结构屈曲失效模式所对应的极限状态函数[26]可表示为

图1 锥体结构示意图Fig.1 Schematic view of a conical structure

(16)

式中：E和ν分别为锥体材料的弹性模量和泊松比。

锥体结构尺寸和载荷的详细参数如表3所示。依据(16)式及表3中所列随机参数的分布信息，分别利用HL-RF方法、FRC方法、TANA方法与本文所提出的SACS-TANA方法近似计算上述极限状态函数所对应的可靠度系数，迭代计算结果如图2所示。

表3 锥体结构尺寸及载荷参数Tab.3 Structural and loading parameters ofconical structure

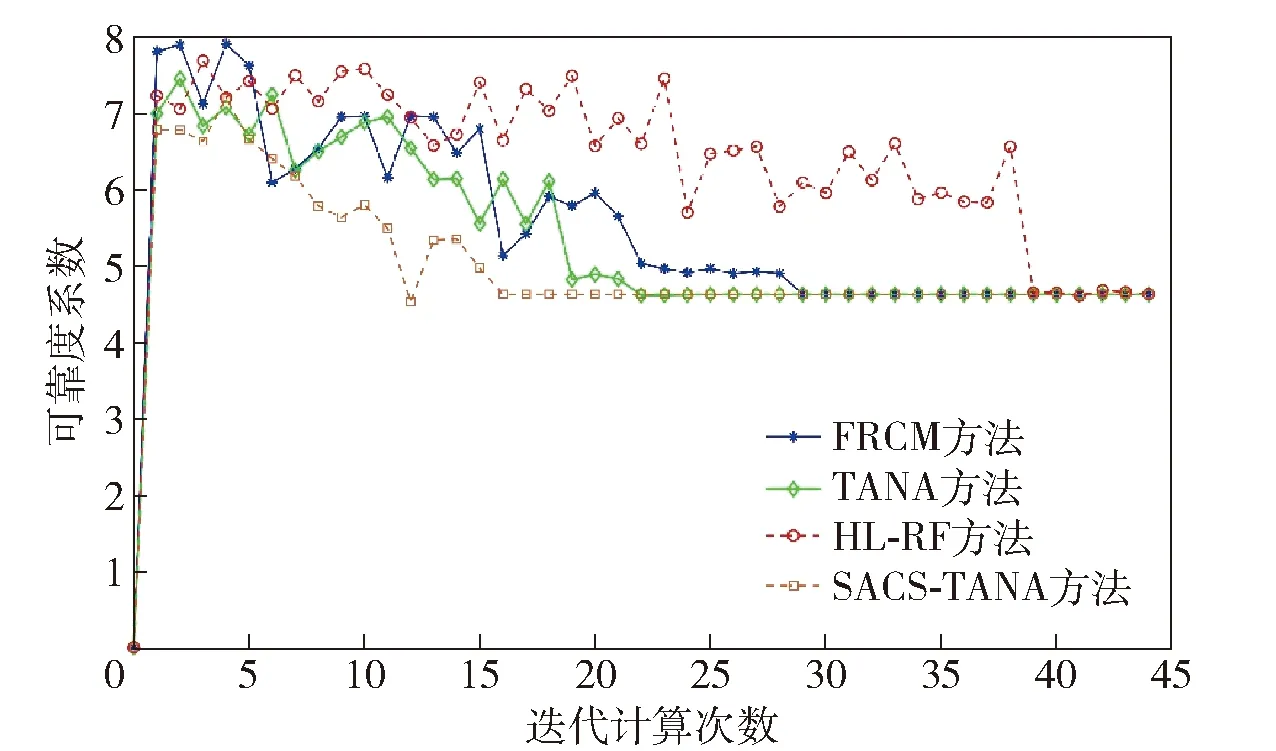
图2 基于不同方法的锥体结构可靠度系数迭代计算过程Fig.2 Iteration calculation process of reliability index of conical structure based on different methods

由图2可以看出，4种方法均可以收敛到最终的准确结果(β=4.632 489)，但相对于其他方法，本文所提出的SACS-TANA方法具有更高的计算效率。

4 结论

针对基于经典FORM的各类结构可靠性方法在求解非线性问题时的数值不稳定性缺陷，本文提出了一种自适应共轭非线性近似方法，通过3个案例验证了该方法的适用性。所得主要结论如下：

1) 相对于基于1阶泰勒级数展开并仅利用当前迭代设计点局部信息的各类迭代方法，由于本文所提方法利用以往迭代设计点的信息构建了自适应非线性近似模型，在保证计算效率的基础上，计算精度较高，对于具有非线性极限状态函数的可靠性分析问题较为适用。

2) 本文所提出的自适应共轭非线性近似方法，在TANA方法的基础上，基于以往两步迭代设计点信息，构建了自适应共轭搜索方向。相比于仅利用最速下降搜索方向的各类方法，本文所提方法在保证计算精度的基础上，计算稳定性更高。