基于码载偏离度的改进自适应Hatch滤波算法
2021-05-06胡杰章林朱倚娴周玲
胡杰, 章林, 朱倚娴, 周玲
(1.中国电子科技集团公司第二十八研究所, 江苏 南京 210007; 2.空中交通管理系统与技术国家重点实验室, 江苏 南京 210007;3.南通大学 机械工程学院, 江苏 南通 226019; 4.运城学院 物理与电子工程系, 山西 运城 044000)
0 引言
基于标准卫星信号的导航系统无法满足终端区精密进近着陆导航性能需求[1-2],因此,国际民航组织(ICAO)提出在终端区对卫星信号进行增强。地基增强系统(GBAS)通过地面站子系统播发伪距校正值和完好性参数提高了机载导航性能[3]。基于全球定位系统(GPS)L1 C/A码GBAS已经获得ICAO I类精密进近着陆许可认证[4]。为提高终端区进场线路设计灵活性,ICAO提出未来将利用GBAS代替传统陆基导航系统,用于支持飞机实现I类甚至更高精度等级精密进近着陆。
载波相位测距精确高,且受多路径影响小,因此在进行导航数据处理前需要进行平滑预处理,以提高系统精度[5]。文献[6]给出了Hatch滤波器算法推导过程,其本质是利用算术平均获得伪距测量值低频部分,利用时间差分算子获得载波相位测量值高频部分,以提高伪距测量精度,目前在卫星导航数据处理领域得到广泛应用。由算法原理知,滤波器平滑时间越大,其带宽越小,则噪声抑制效果越好。但是卫星信号观测值中的伪码- 载波偏离度会导致Hatch滤波器输出一项额外的常值偏置误差。根据分析知,该项误差与滤波器平滑时间呈正比,因此必须选择一个适合的平滑时间[7]。美国联邦航空局(FAA)研究报告指出,GBAS中Hatch滤波器平滑时间宜设置为100 s固定值[8],但是相关学者研究表明,对于所有可见卫星在全时间段内使用固定平滑时间缺乏合理性,例如,当卫星仰角较低时伪距所受多径效应较为明显,此时宜提高滤波器平滑时间以抑制高频噪声。由于GPS L1是目前唯一获得ICAO认证的用于卫星信号增强频点[9],为提高系统精度与完好性,许多学者进行了相关技术攻关。文献[10]为抑制算法发散对Hatch滤波器系数进行归一化,但是其最优系数设置受限较大。文献[11]建立了电离层延时分段线性模型,其相比常规线性模型更加符合实际特性,但该方法计算量相对较大,影响了算法的实时性。文献[12]建立了平滑时间与电离层风暴梯度数学模型,给出了滤波器最优平滑时间估计方法,当电离层异常时该方法假设平滑时间为无穷大,该假设在实际中并不成立,且在计算最优平滑时间时并未考虑伪距测量噪声影响。文献[13]利用Klobuchar模型对电离层延时进行建模并根据可见卫星仰角大小自适应确定Hatch滤波器平滑时间,分析该文献可知,电离层延时建模结果与实际值之间存在较大偏差,因此导致滤波器平滑精度不能保证。文献[14]提出一种电离层异常检测算法,并利用低通滤波器抑制伪距测量噪声以及实现电离层延时变化率在线估计,分析该文献可知,电离层延时检测灵敏度与低通滤波器时间常数呈反比,当模拟数值大小为0.012 m/s的电离层延时变化率时,低通滤波器响应时间为94 s,其估计电离层延时变化率的灵敏度低,且其在计算最优平滑时间时未考虑伪距噪声标准差对平滑时间估计影响。
本文提出一种适用于单频GBAS的自适应Hatch滤波算法,该算法根据卫星信号伪码- 载波偏离度在线估计电离层延时变化率和伪距测量噪声标准差,并推导得到平滑后伪距误差均方根与电离层延时变化率、伪距测量噪声标准差以及滤波器平滑时间三者之间的函数模型,进一步根据该函数表达式计算得到滤波器最优平滑时间。
1 码减载波建模及电离层延时变化率估计
卫星信号伪距和载波相位测距观测方程[15]可表示为
(1)
式中:ρ、φ分别表示接收机输出伪距和载波相位测量值;r为一项等效距离,由卫星与接收机之间几何距离、接收机和卫星钟差以及对流层延时等组成;ι表示电离层延时;N表示载波相位整周模糊度;Mρ、Mφ分别表示伪距和载波相位测量噪声。
任意t时刻利用伪距和载波相位测量值做差可得该颗卫星的码减载波,即
yt=ρt-φt=2ιt-N+Mt,ρ-Mt,φ,
(2)
式中:yt表示t时刻伪距和载波相位测量差值;ρt、φt分别表示t时刻伪距和载波相位测量值;ιt表示t时刻电离层延时;Mt,ρ、Mt,φ分别表示t时刻伪距和载波相位测量噪声。
由(2)式可知,码减载波值中包含2倍电离层延时、载波相位整周模糊度、伪距和载波相位测量噪声等。电离层延时具有随时间变化特性,但是在短时间内一般可认为其具有线性变化特性,因此,(2)式又可表示为
yt=b+2t·a+Mt,ρ-Mt,φ≈b+2t·a+Mt,ρ,
(3)
式中:b表示常值项;a表示电离层延时变化率,由于载波相位测量噪声相比伪距测量噪声要小很多,其可以忽略不计,将t1~tn时间段内的码减载波写成矩阵形式,n表示大于1的自然数,其中tn-t1取值为60 s,可表示为
(4)
即
Y=Xβ+M.
(5)

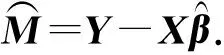
(6)
图1所示为一组GPS卫星观测数据中10号卫星7 200 s内码减载波随时间变化曲线,由于码减载波中包含载波相位整周模糊度,设置码减载波初始值为零。计算得到的码减载波噪声较大,本文利用滑动平均滤波器进行平滑预处理,平均滑口大小设置为800 s,经过滑动平均滤波后的码减载波反映了当前卫星所受电离层延时变化大小和趋势。

图1 10号卫星码减载波曲线Fig.1 Code-minus-carrier curve of Satellite 10
进一步利用最小二乘法可计算得到电离层延时变化率a,其中tn取值为60 s,因此系统每间隔60 s更新一次电离层延时变化率计算值。当卫星截止角设置为10°时,10号卫星在天顶方向可见总时长为20 254 s,因此共进行了337次最小二乘求解电离层延时变化率,如图2所示。为了验证最小二乘法估计得到的电离层延时变化率的准确性,本文以双频载波相位测量值计算得到的电离层延时变化率作为参考比较对象,其计算过程为
(7)
ΔId,t=SL1,t-SL1,t-1,
(8)
式中:SL1,t、ΔId,t分别表示t时刻根据接收机输出L1和L2频点载波相位测量值计算得到的电离层延时及其变化率;fL1、fL2分别表示接收机输出L1和L2测量频率;φL1、φL2分别表示L1和L2频点载波相位测量值;NL1、NL2分别表示L1和L2频点载波相位整周模糊度。

图2 电离层延时变化率估计曲线Fig.2 Estimated curve of ionospheric delay rate
对比图2中蓝色和红色曲线可以看出,本文建立的码减载波线性模型能够较好地估计得到电离层延时变化率,在此基础上可以分离得到伪距测量噪声,并进一步计算其标准差。
2 基于码载偏离度的平滑时间自适应确定方法
2.1 Hatch滤波器误差分析
任意k时刻Hatch滤波器离散递推形式[16]可表示为
(9)
式中:ρs,k、ρs,k-1分别表示k和k-1时刻平滑后伪距测量值;K表示滤波器平滑时间;ρk表示k时刻伪距测量值;φk、φk-1分别表示k和k-1时刻载波相位测量值。经Hatch滤波器平滑后的伪距误差εk可表示为
εk=ρs,k-ρk.
(10)
(9)式代入(10)式,可得平滑后伪距误差表达式为
(11)
式中:Mρ,k表示k时刻伪距测量噪声。
假设ε初始值为0,电离层延时变化率为a,则由(11)式可得平滑后伪距误差递推解为
(12)
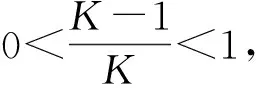
(13)
由(13)式可知,平滑后伪距误差包括系统误差和随机误差两部分,其中,λ表示系统误差,Δ表示随机误差。系统误差由电离层延时变化率和滤波器平滑时间构成,随机误差则由伪距测量噪声和滤波器平滑时间构成。稳态误差εss可以表示为电离层延时变化率、伪距测量噪声和滤波器平滑时间的函数。当电离层延时变化率不等于零时,经Hatch滤波器平滑后伪距会产生一项偏置误差,其大小与滤波器平滑时间呈正比,例如,当a=5 mm/s、滤波器平滑时间设置为100 s时,该误差项最大为1 m,因此滤波器平滑时间不宜设置过大。同时,由伪距平滑后随机误差可知,滤波器平滑时间K值越大,则伪距噪声抑制效果越好,为了提高伪距平滑精度需要增大K值,实际应用中需要根据卫星信号传播环境自适应确定滤波器平滑时间。
2.2 计算最优平滑时间
由(13)式可知,平滑后伪距误差中系统误差和随机误差可表示为
λ=-2(K-1)a,
(14)
(15)
进一步根据(14)式和(15)式,可计算得到平滑后伪距误差均方根RMS为
(16)
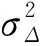
(17)
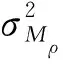
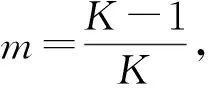
(18)
λ2=4(K-1)2a2.
(19)
(18)式和(19)式代入(16)式中,有
(20)
由(20)式可知,平滑后伪距误差均方根大小由Hatch滤波器平滑时间、电离层延时变化率以及伪距测量噪声标准差决定,如(21)式所示:
RMS(εss)=f(K,a,σMρ).
(21)
分析(21)式可知,当a和σMρ已知时,函数f(K,a,σMρ)最小值时所对应的K值即为最优平滑时间,对 (21) 式求偏导数,可得
(22)
(22)式进一步可整理简化为
(23)
本文利用Cardano法实现(23)式解析求解,其中Cardano法求解三次方程过程如(24)式~(27)式所示,假设三次方程表示为
x3+αx2+βx+γ=0,
(24)
式中:x表示三次方程待求解未知根;α,β,γ∈R.
利用Cardano方法可得(24)式的解析解为
(25)
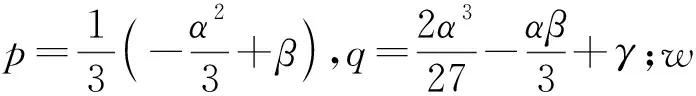
由于滤波器平滑时间为正整数,(23)式的正实根取整即为所求最优平滑时间Ko:
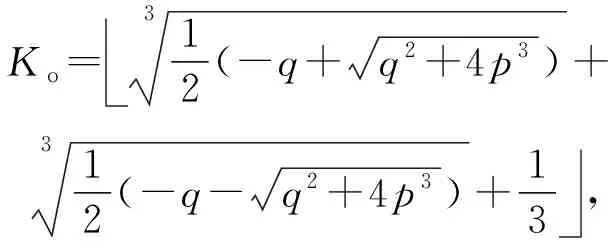
Ko=312(-q+q2+4p3)+312(-q-q2+4p3)+13,
(26)
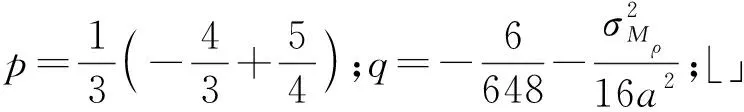
图3为最优平滑时间Ko随电离层延时变化率a和伪距测量噪声标准差σMρ变化三维曲面图,a取值范围为0.1~8 mm/s,σMρ取值范围为0.01~6 m. 由图3可以看出,Ko取值与σMρ呈正比,与a呈反比,即σMρ值越大,a值越小,则对应的Ko值越大。
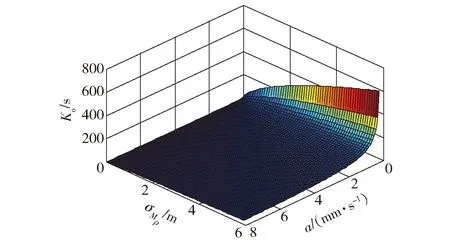
图3 最优平滑时间Ko随a和σMρ变化三维曲面图Fig.3 Three-dimensional surface graph of the optimal smoothing time Ko changing with a and σMρ
综上所述,本文所提出的自适应Hatch滤波算法流程如图4所示。

图4 自适应Hatch滤波算法流程Fig.4 Flowchart of adaptive Hatch filter algorithm
首先,依次计算所有可见卫星的码减载波,建立其1阶线性模型,并利用最小二乘法估计电离层延时变化率a和伪距测量噪声标准差σMρ;然后,利用1阶线性时不变低通滤波器进行滤波处理,以平滑高频噪声;最后,根据计算得到的a和σMρ以及最优平滑时间计算公式确定得到Ko值,该值即为Hatch滤波器最优平滑时间。
3 验证实验
3.1 实验环境
利用实验室研制GBAS原理样机进行验证实验,该系统实时接收GPS卫星信号后经过数据处理中心后输出伪距差分校正值和完好性参数等。GBAS地面系统由基准站、数据处理中心、VDB发射电台等组成,模拟机载用户(位置域)由机载多模接收机、机载数据处理中心以及VDB接收电台等组成,GPS卫星接收天线架设在实验室楼顶,如图5所示。
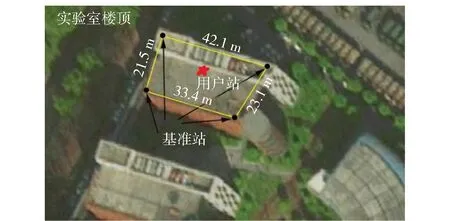
图5 GBAS地面系统GPS天线Fig.5 GPS antennas of GBAS ground subsystem
3.2 结果分析
以一组用户站接收机输出GPS卫星信号伪距和载波相位测量数据为例,对本文所提算法进行验证,其中,码减载波滑动平滑窗口长度设置为800 s,a和σMρ每间隔60 s更新一次,因此最优平滑时间Ko也是每间隔60 s更新计算一次。图6为其中1号卫星估计得到的a和σMρ随时间变化曲线,图7为利用估计得到的a和σMρ计算得到的Ko随时间变化曲线,图8为1号卫星仰角随时间变化曲线。
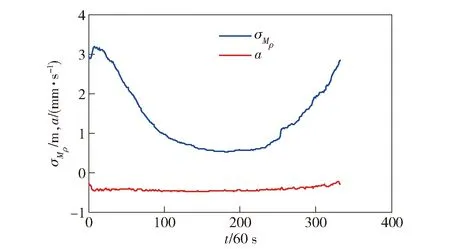
图6 1号卫星a和σMρ随时间变化曲线Fig.6 a and σMρ of Satellite 1 changing with time
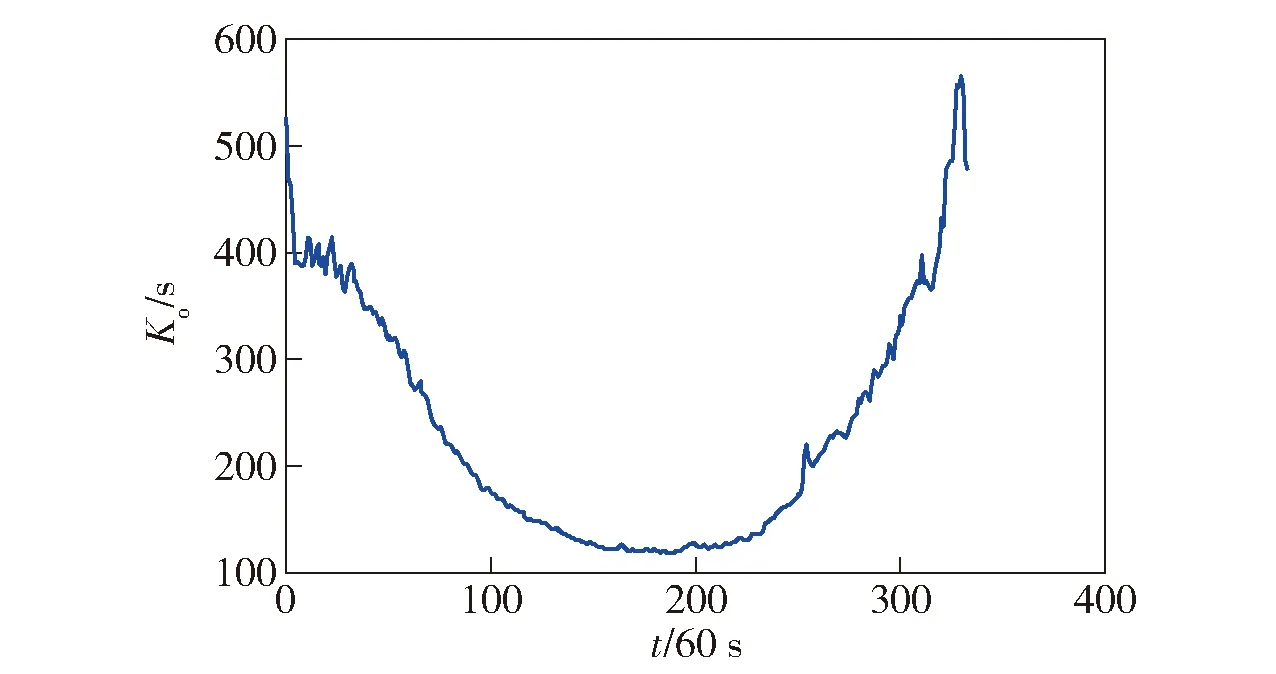
图7 1号卫星Ko随时间变化曲线Fig.7 Ko of Satellite 1 changing with time
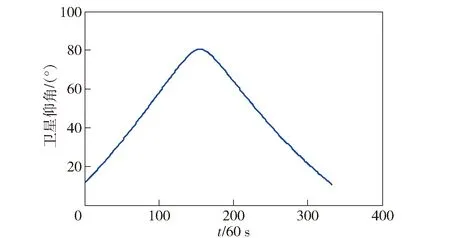
图8 1号卫星仰角随时间变化曲线Fig.8 Elevation angle of Satellite 1 changing with time
由图6和图8可以看出:σMρ随着卫星仰角的增大而减小,表明卫星仰角越低,伪距所受多路径越大;a值变化较为平稳,也进一步表明电离层延时在较短时间内可认为具有线性特性。由图7可以看出,当电离层变化平稳时,Ko随σMρ值的增大而变大,即卫星仰角较低时,宜增大Ko值,以抑制伪距测量随机误差。
图9给出了模拟机载用户3 600 s内差分定位误差曲线。为了凸显本文所提算法的有效性,分别利用固定平滑时间Hatch滤波器和本文所提自适应Hatch滤波算法对伪距进行平滑,δx、δy和δz分别表示x轴、y轴和z轴3个方向位置误差。图10给出了该时间段内GPS可见卫星仰角随时间变化曲线。
由图9可以看出,自适应滤波算法位置解算精度较高,特别是在1 200~2 000 s之间,自适应滤波算法精度优势更加明显,根据图10可知,在1 200~2 000 s之间最多有4颗卫星仰角低于15°,即20号、22号、29号以及12号卫星,因此这一时间段内相应伪距所受的多路径也较大,利用自适应滤波算法能够更好地起到平滑滤波效果,位置解算精度也相对较高。
为进一步验证本文所提出算法的有效性,分不同时间段(早上8:00—9:00,中午11:00—12:00,晚上19:00—20:00)进行3组验证实验,每组持续时间为3 600 s,表1为两种滤波方法对应的位置误差均方根值对比统计结果。
由表1可以看出,中午太阳光辐射强时,卫星信号所受电离层延时最大,因此其对应差分定位精度也相对最差。同时可以看出,当采用本文所提出的自适应Hatch滤波算法时3个方向位置解算精度相比传统100 s固定平滑时间算法都得到了提升,其中,实验2中x轴方向位置精度最大提高了53.19%,由此进一步验证了本文所提方法的正确性。
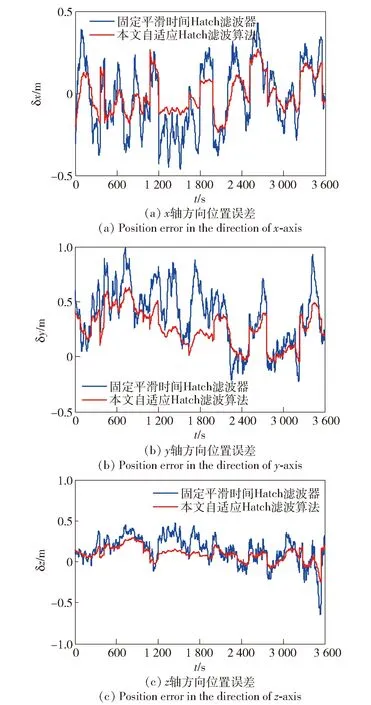
图9 不同滤波方法位置误差对比曲线Fig.9 Comparison of position errors of different filtering methods
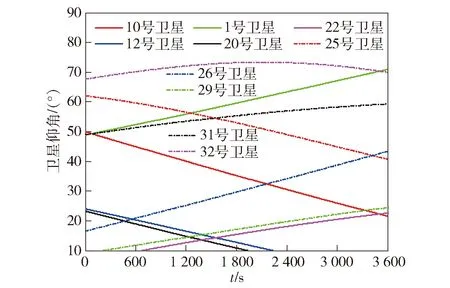
图10 可见卫星仰角变化曲线Fig.10 Changing curves of elevation angles of all visible satellites
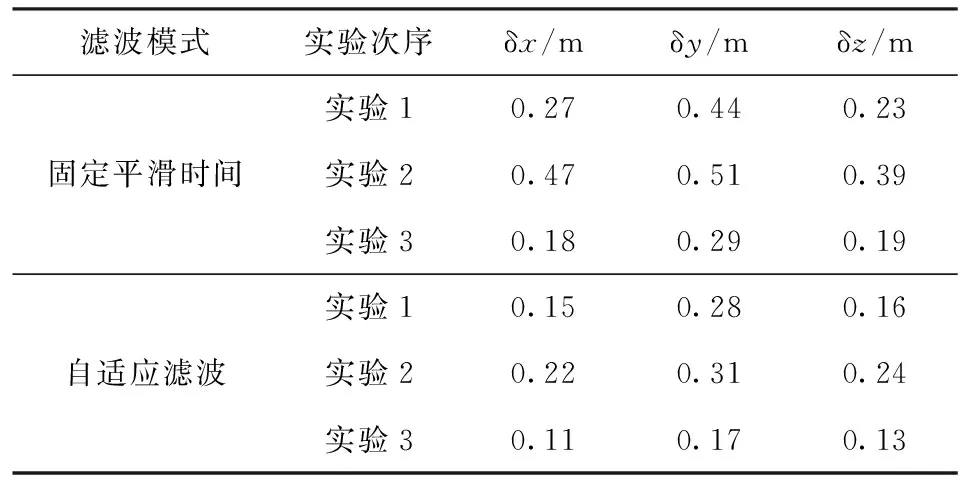
表1 位置误差均方根值对比统计Tab.1 Statistical comparison of RMSs of position errors
4 结论
为提高单频GBAS中载波相位平滑伪距精度,本文针对Hatch滤波器平滑精度易受电离层延时和伪距测量噪声影响的问题进行了分析和研究。得到以下主要结论:
1) 电离层延时短时间内具有线性变化特性,码减载波值反映了2倍电离层延时,通过建立码减载波1阶线性模型,在此基础上利用最小二乘法能够估计得到电离层延时变化率。
2) 根据Hatch滤波算法推导得到平滑后伪距误差均方根函数模型,该函数模型大小由电离层延时变化率、伪距测量噪声标准差以及平滑时间决定,由此进一步可得滤波器最优平滑时间。
3) 进行了系统验证实验,结果表明本文所提算法能够根据卫星信号实际环境自适应确定最优平滑时间;模拟机载用户(位置域)差分定位结果表明本文所提出的自适应滤波算法3个方向位置解算精度相比固定100 s平滑时间都有提高,表明了本文所提算法的正确性。
