多基地雷达组网布站优化方法
2021-05-06李海鹏冯大政周永伟董普靠
李海鹏, 冯大政, 周永伟, 董普靠
(1.西安电子科技大学 雷达信号处理国家重点实验室, 陕西 西安 710071; 2.西安电子工程研究所, 陕西 西安 710100)
0 引言
多基地雷达是由空间上多个分散布置的发射站和接收站组成的雷达系统[1],与单基地雷达相比,多基地雷达在反隐身、抗干扰、目标定位和跟踪等方面具有明显的优势[2-5]。但是发射站与接收站的布站位置对多基地雷达具有重要的影响。文献[6]指出发射站与接收站的位置与模糊函数的性能紧密相关。文献[7]基于一种正交频分复用的线性调频信号分析布站位置对模糊函数性能的影响,发现优化接收站和发射站的位置和数量可以改善模糊函数性能。该方法依赖发射信号的参数,当改变发射信号后需要调整当前的优化结果,实时性较差。文献[8]针对无源时差定位误差的克拉美罗下界,提出一种利用克拉美罗下界迹的平均值最小为准则的优化方法,但该方法仅优化了接收站位置。基于雷达探测区域覆盖的布站优化方法可以同时优化接收站和发射站的位置,且对发射信号变化不敏感。文献[9]通过最小化兴趣点(PoIs)到其最近接收站和发射站的最大距离积来优化多基地雷达的布站位置,雷达探测区域仅覆盖兴趣点。文献[10]将连接覆盖区域两侧边界的最短线段称为布置线,并指出基于布置线的栅栏覆盖[11]是最优布站,最后通过最小化栅栏脆弱性的方法求解布站优化问题,该方法没有限制栅栏的最小覆盖宽度,因此当覆盖宽度较小时,雷达可能会无法探测到高速通过的目标。文献[12]基于部署费用最小的原则,提出一种利用穷举法优化的同构布站方法(UPDA_EM),该方法要求在单条布置线上使用相同的布站模式,末端根据剩余长度布置发射站或者接收站,因此单条布置线的端点至少有一个是发射站。从部署费用上讲,将发射站作为布站端点会增大费效比,且采用穷举法求解最优布站参数的计算量较大。
为解决文献[12]存在的不足,本文通过分析布站模式覆盖区域的关系,提出单条布置线上布站优化应满足的条件,并基于此提出一种采用缩减穷举法优化的异构布站方法(HPDA_REM),该方法的创新点如下:1)在布置线上采用异构模式布站,保证布置线两端布置接收站;2)缩小穷举法搜索范围,降低计算量,仿真结果表明HPDA_REM可以取得更低的部署成本,且计算量明显减少;3)由于HPDA_REM优化结果中需要的发射站更少,在电子战中有利于降低反辐射导弹对雷达系统的威胁。
1 概念与记号
对于一发多收的多基地雷达系统,可将其发射站与每个接收站分别看成一个双基地雷达。因此可通过双基地雷达说明多基地雷达的覆盖区域。
空间任意一点z到接收站R和发射站T的斜距分别记作Rr(z)和Rt(z),简记为Rr和Rt. 实际应用中雷达往往工作在杂波环境和干扰环境下,因此接收天线输出端的信号中还包含热噪声No、杂波Co和干扰Jo. 此时脉冲多普勒双基地雷达的基本方程为
(1)
式中:Pa为平均功率;tc为相参处理间隔(CPI);Gr、Gt分别表示接收天线和发射天线的增益;λ为信号波长;σb为目标雷达截面积;Ft、Fr分别表示发射和接收方向图的传播因子;Io为热噪声、杂波和干扰在接收天线输出端产生的总能量,Io=Jo+Co+No;D(i)为检测因子,i为进行相干积累的脉冲数量[13];L为系统损耗因子;假设σb不变,Kb为由双基地雷达物理参数所确定的常量[14]。记SINR(z)为目标在z点时接收天线输出端的信干噪比,记信干噪比门限SINRmin=γ. 则当SINR(z)≥γ时,认为目标可被雷达系统检测到,即目标处于雷达覆盖区域内;反之,信号将被淹没在杂波和干扰中,不能被有效检测出来。因此,所有满足SINR(z)≥γ的z点所构成的区域是双基地雷达覆盖区域,由(1)式可得
(2)


图1 双基地雷达覆盖区域类型Fig.1 Bistaitc radar coverage area categories

记由1个发射站和m个接收站组成的布站模式为Pm=(T,R1,…,Rm),其覆盖长度记为σp(m);由第j、第j+1个发射站和n个接收站组成的布站模式为Fn=(Tj,R1,…,Rn,Tj+1),其覆盖长度记为σf(n),如图2所示。图2中,2d1表示第1个接收站与其相邻发射站之间的距离,2dk(k≥2)表示第k-1个和第k个接收站之间的距离。值得注意的是,布站模式Fn中站点布置具有对称性,因此接收站Rn与发射站Tj+1之间的距离等于2d1,接收站Rn与Rn-1之间的距离等于2d2. 更进一步,由模式Pm和Fn可以构成布站模式Gn,m=(Tj,R1,…,Rn,Tj+1,R1,…,Rm)。由图2可知,其覆盖长度σg(n,m)=σp(m)+σf(n)。以上模式的覆盖长度均不包括端点发射站以外的部分。
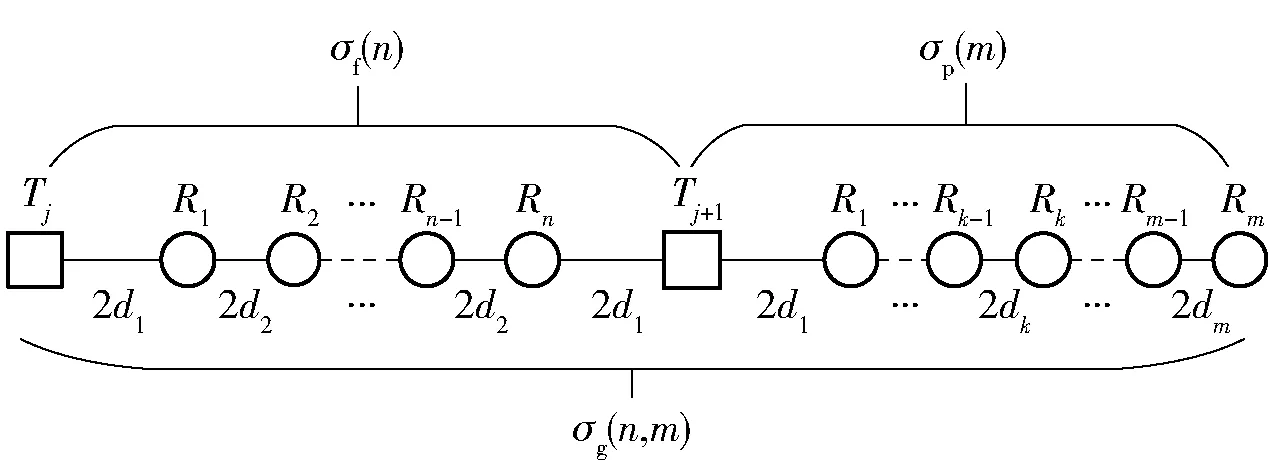
图2 Fn和Pm模式的覆盖长度Fig.2 Coverage area lengths of Fn and Pm
因此,基于总布站费用最小的布站优化问题表述为:假设雷达覆盖的目标区域C可用一个长为D、宽为H的矩形S近似,如图3(a)所示。选择布站模式,使用多个发射站和接收站构成满足覆盖需求的多基地组网雷达覆盖区域,并且要求总布站费用最低。受文献[12]启发,使用q条平行于长边D的布置线,每条布置线对应1个栅栏覆盖,则在等分宽度的情况下,单个栅栏覆盖的宽度为2h=H/q,如图3(b)所示。图3中,T1、T2为发射站,R1、R2、R3、R4、R5为接收站。
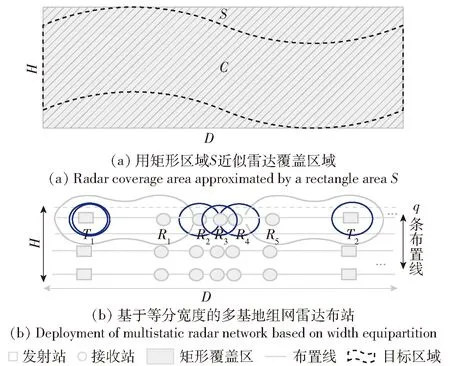
图3 多基地雷达组网覆盖区域示意图Fig.3 Schematic diagram of coverage area of multistatic radar network
于是,布站优化问题可表述为
(3)
本文假设多基地雷达系统内所有发射站都相同,且使用相互正交的工作频率以避免发射站干扰[15]。所有接收站均相同,接收站的工作频率可选以匹配相应的发射站。
2 布站优化方法与优化模型
下面通过分析不同布站模式的覆盖长度关系,提出本文布站策略的理论基础与算法。
2.1 布站模式覆盖长度的计算

(4)
(5)
由(4)式、(5)式可知,覆盖长度由序列xn的和决定,且由引理1可知σf(n)与σp(m)均随着接收站数量增多而增大,但增大的幅度逐渐减小,即当接收站远离发射站时,其对增加覆盖长度的作用较小。
引理1序列{xn,0≤n<0.5(β2-1)}是严格单调递减序列。
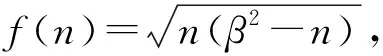
2.2 剩余长度的布站优化方法
文献[12]依据剩余长度在布置线端点选择发射站或者接收站,此时单条布置线上一端或者两端为发射站,而端点布置发射站会导致费效比增大,因此布站成本仍有优化空间。本文通过引理2说明如何在布置线两端优化分配剩余长度,并说明此时布站模式Pm、Fn之间的关系。
引理2设max{n,m}≤Nmax,则
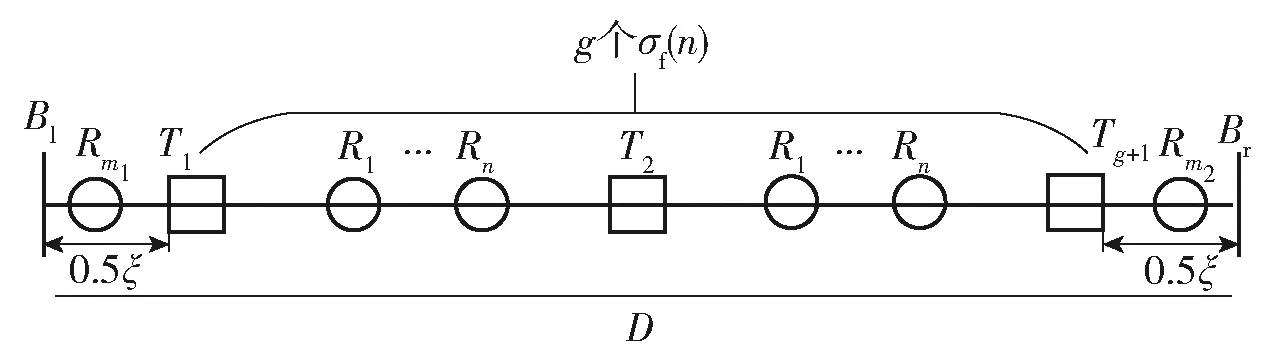
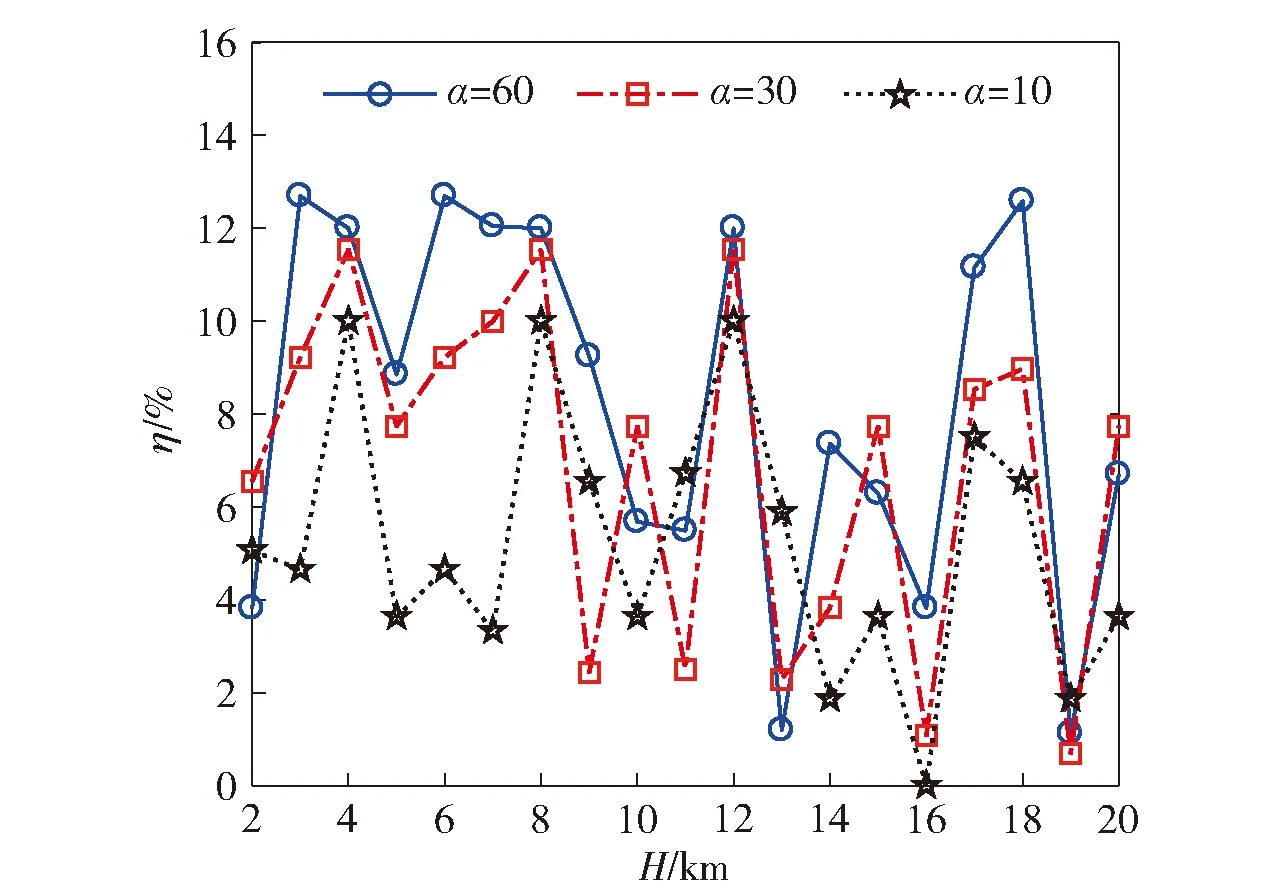
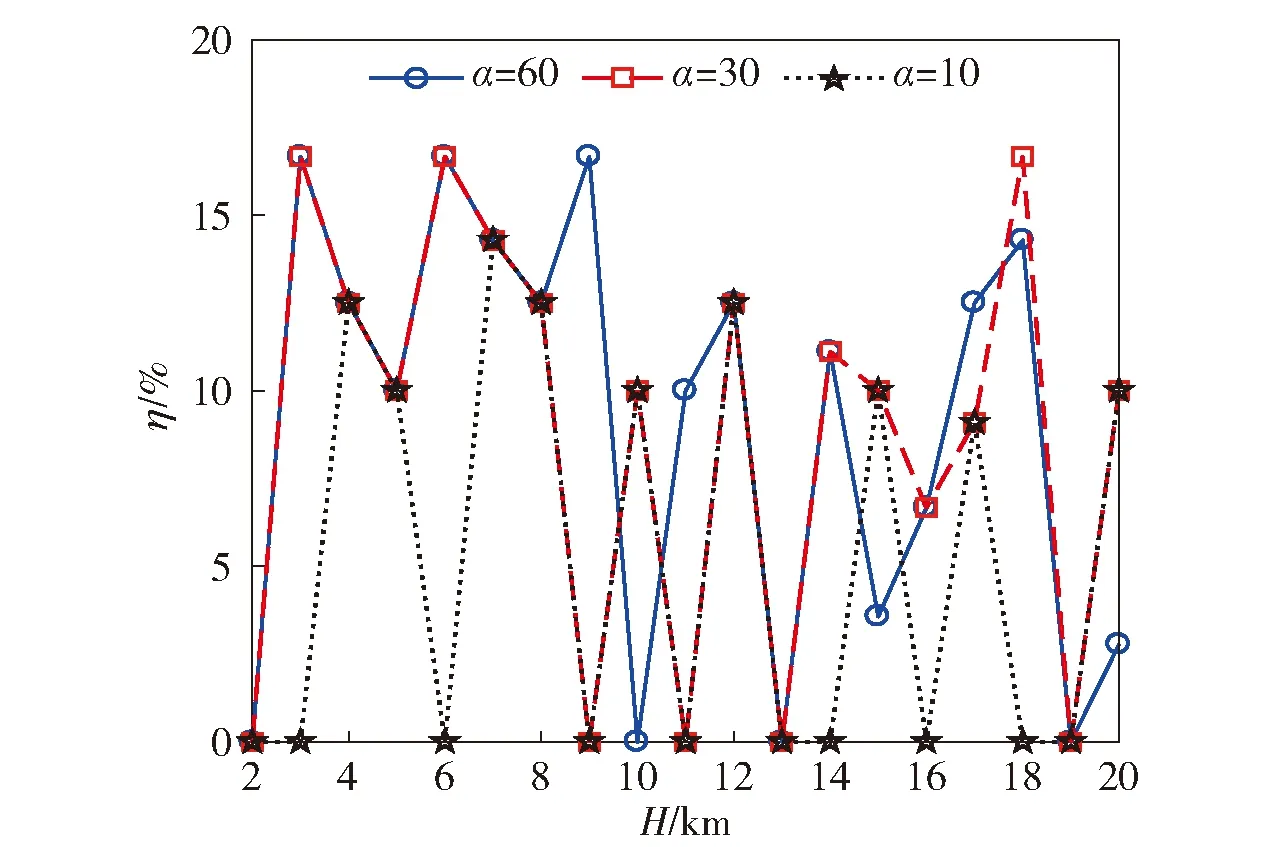
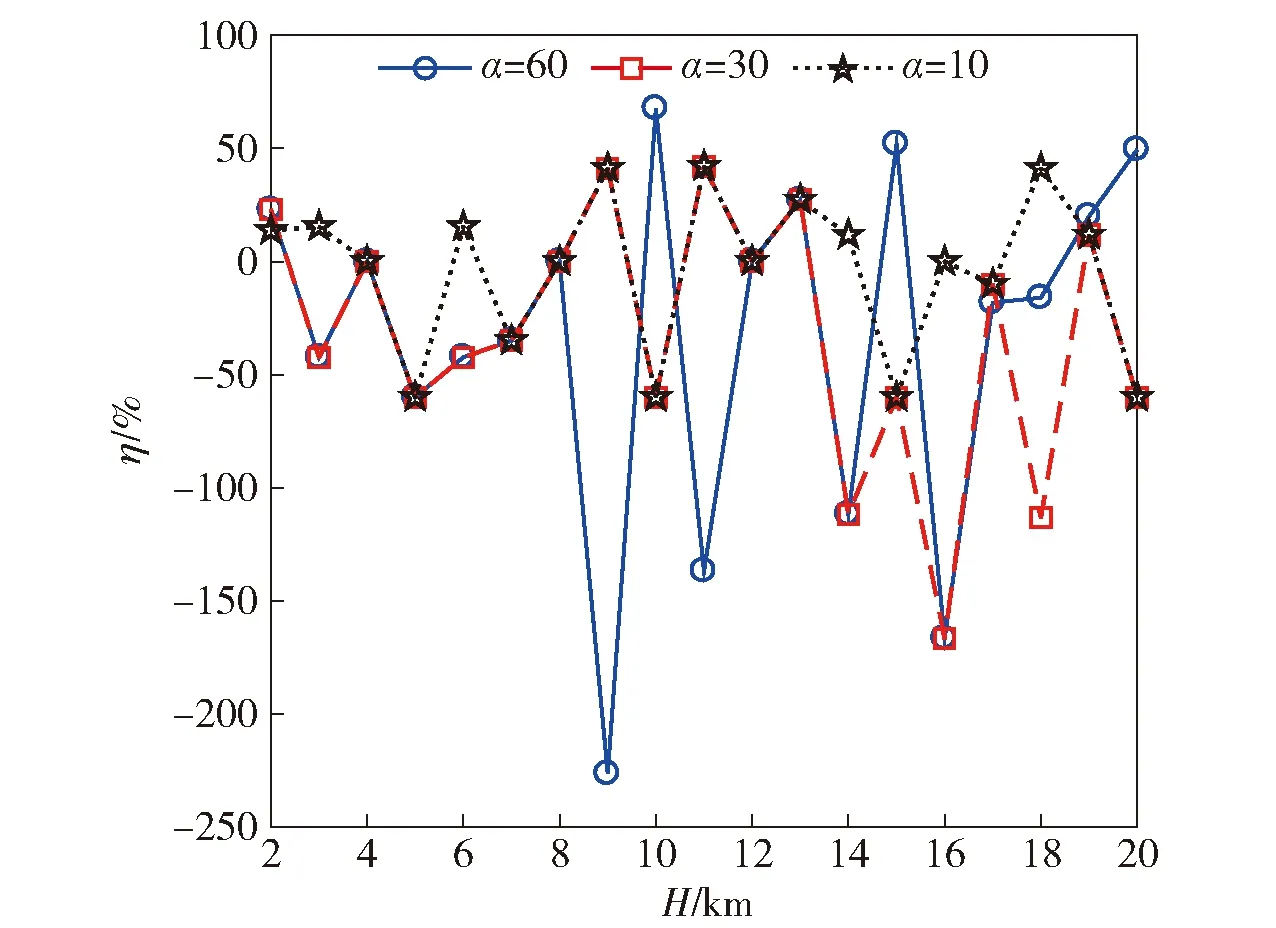
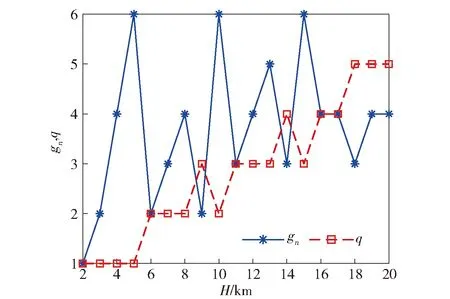
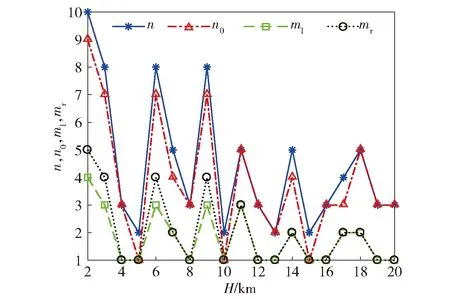
1)当n (6) 2)若n≠m,则有σp(n)+σp(m)<σf(n+m)<2max {σp(n),σp(m)}。 3)当n=m时,σf(n+m)=2σp(n)。 证明1)先证明n+m=2l为偶数的情况,l∈N+. 由(4)式、(5)式可知: 2)由引理1与(6)式可得左边不等式成立。以下证明右边不等式成立,不失一般性,假设n 同理可证当n+m为偶数时右边不等式也成立。综上所述可知原不等式成立。 3)由(4)式、(5)式易证等式成立。 引理2的第2条说明当n为奇数且m1=(n-1)/2、m2=(n+1)/2时,模式Fn的覆盖长度大于模式Pm1与模式Pm2的覆盖长度和,但小于2个模式Pm2的覆盖长度和。引理2的第3条说明当n=2m时,模式Fn的覆盖长度可由两个模式Pm的长度和等量替代。因此当矩形区域长为D时,用g个Fn模式覆盖后的剩余长度为ξ=D-gσf(n)<σf(n)≤2σp(m),即一定可用2个Pm覆盖剩余长度,其中g=⎣D/σf(n)」,m=⎣(n+1)/2」,此时单条栅栏的布站如图4所示,其中Bl与Br分别代表矩形的左右边界。 图4 单条栅栏的布站示意图Fig.4 Illustration for the deployment of one barrier 为了降低第1个和第g+1个发射站的费效比,将剩余长度等分后分别采用1个Pm模式覆盖,此时在栅栏两端分别构成1个布站模式Gn,m. 下面通过引理3分析σg(n,m)取得最大值的条件,提出模式Gn,m中接收站的布站优化方法。 引理3设max{m,m1,m2}≤Nmax,n≤2Nmax: 1)当m1+m2给定时,若|m2-m1|≤1,则σp(m1)+σp(m2)的值最大。 2)当n+m给定时,若|n-2m|≤1,则布站模式Gn,m的覆盖长度σg(n,m)值最大。 证明1)不失一般性,假设m1≤m2,当m1+m2=2l为偶数时,由(6)式可得 由引理1可知当m1=m2时,σp(m1)+σp(m2)值最大;同理可证若m1+m2=2l+1为奇数,则当m1=m2-1时σp(m1)+σp(m2)最大。 2)对n+m的取值分以下3种情况证明: ①n+m=3v-1;②n+m=3v+1;③n+m=3v. 其中v∈N+. 同理可证明其他情况。 引理1指出远离发射站的接收站,对增加栅栏覆盖长度的贡献不如近距离的接收站。因此由引理3所述,在Gn,m模式中优化布置接收站,使得σg(n,m)最大。 此时对于矩形区域的长D,使用g个Fn模式构成单条栅栏覆盖,所得剩余长度为ξ=D-gσf(n)。用模式Gn0,mr,Gn0,ml覆盖长度2σf(n)+ξ,由以下引理4可知,当n≥n0≥n-2且|n0-2ml|≤1,|n0-2mr|≤1时,单条布置线上布站方式最优。这里,n0为模式Fn0中接收站的个数,mr和ml分别为模式Pmr和Pml中的接收站个数。 引理4设单条布置线上使用的布站方法为:中间g-2个Fn模式,两端分别为模式Gn0,m1与Gn0,mr,则此时布站方法最优的充分条件是n≥n0≥n-2,且|n0-2ml|≤1,|n0-2mr|≤1. 证明由文献[12]引理2可知,当|n0-n|≤2时,σf(n)+σf(n0)覆盖长度最大,再由引理3可知,当|n0-2m1|≤1、|n0-2mr|≤1时,σg(n0,m1)与σg(n0,mr)值分别取得最大。于是,当|n0-n|≤2且|n0-2m1|≤1、|n0-2mr|≤1时,(g-2)σf(n)+σg(n0,m1)+σg(n0,mr)的值最大。 下面通过反证法证明n0≤n. 若n0>n,则由引理2知ξ0=σf(n)+0.5ξ可用模式Gn,⎣(n+1)/2」覆盖,因此Gn0,m1的接收站之和不超过Gn,⎣(n+1)/2」的接收站之和,即m1≤n-n0+⎣(n+1)/2」,又因为n0-2m1≥3n0-2n-2⎣(n+1)/2」>1,与|n0-2m1|≤1矛盾,因此n0≤n. 特别地,若|n0-2m1|≤1、|n0-2mr|≤1,则易得|m1-mr|≤1. (7) 式中:f(q,n,n0,ml,mr)=q(g(n+α)+α+2(n0-n)+ml+mr)cr. 由(7)式可知,布置线数量q确定了布站模式中接收站数量的最大值,且q的取值范围是有限的,因此可以通过穷举法计算所有满足引理4条件的布站成本,然后通过成本最小准则找到最优解。值得注意的是,通过缩小q的取值范围,可以有效减少穷举法的计算量。引理5用于说明如何确定q的上限阈值qsup. qsup≜qmin[(g0+1)(α+1)+1]ψ+α,qmin=H2hmax=3H2Lmax,「⌉ g1=Dσf(1),ψ=min(q,n)[g(n+ 引理5当栅栏数q>qsup时,总布站费用不会取到最小值。其中表示向上取整,α)+2(B-n)],Bmax{n-2,1},n为模式Fn中可能的接收站数量。 当q=qmin时,单条布置线上的布站模式为g0个F1,max{ml,mr}≤1,则此时总部署费用不会超过qmin((g0+1)(α+1)+1)。由引理4可知,Bmax{n-2,1}≤n0,因此q{(g+1)α+(g-2)n+2n0+ml+mr}≥q{(g+1)α+(g-2)n+2B+ml+mr}≥q{(g+1)α+2B+(g-2)n}=q(g(n+α)+2(B-n)+α)≥q(ψ+α). 于是当q(ψ+α)>qmin((g0+1)(α+1)+1)时,总部署成本不可能取得最优值。因此布置线范围的上限阈值为 综上所述,本文所提算法具体步骤如下: qmin=3H2Lmax,qsup=qmin((g0+1)(α+1)+1)ψ+α. 步骤1计算布置线个数的下限和上限阈值, 步骤2forq=qmin:qsup,计算Fn中接收站数量的最大值Nmax,初始化总部署成本集合Ctot=∅,∅表示空集。 步骤3forn=1:2Nmax,初始化单条布置线的部署成本集合C1=∅,按照引理4分别确定模式Fn、Fn0、Pm1及Pmr中接收站的个数n、n0、mr、ml. 计算单条布置线上的费用(g-2)n+2n0+(g+1)α+ml+mr,更新C1=C1∪{(g-2)n+2n0+(g+1)α+ml+mr}. 步骤4end for. 步骤6end for. 需要说明的是: 1)若要求一条栅栏覆盖的最小宽度为2τ,则最大栅栏数qmax=「H/(2τ)⎤。此时求解布站优化的搜索域为[qmin,qmax],但通过引理5可以减少搜索域为[qmin,qsup]. 为说明本文所提HPDA_REM的有效性,通过仿真比较HPDA_REM与UPDA_EM的优化结果。实验的基本条件同文献[12],其他仿真参数假设为:最大脆弱性阈值Lmax=5 km,在发射器与接收器费用之比α分别取值为10、30、60时,栅栏长度D=160 km,宽度H由2 km增加到20 km. 定义布站参数变化率η为 η=(γ-γ′)/γ×100%, (8) 式中:γ、γ′分别为按照UPDA_EM与HPDA_REM得到的布站参数。当γ、γ′表示部署成本时,由(8)式可得部署成本变化率曲线,如图5所示。 图5 α分别取值为10、30、60时部署成本变化率Fig.5 Change rates of deployment cost for α=10,30,60 由图5可知,部署成本变化率始终大于0,表明HPDA_REM的部署成本与UPDA_EM相比有不同程度的下降,特别地,当α较大时HPDA_REM可以节省更多的部署费用,最大节约12.69%(H=18 km,α=60). 这是因为HPDA_REM可以充分发挥发射站的作用,在费用比较大时显著提高其成本效率。而当α较小如α=10时有一定的降低效果,当H=8 km时也能达到10.0%. 此时因为发射站与接收站的成本差距较小,UPDA_EM方法“浪费”的发射站成本不明显。由此表明本文所提HPDA_REM可以有效降低布站成本。 当γ、γ′表示发射站总数量时,由(8)式可得发射站变化率曲线,如图6所示。由图6可知,在α分别取值为10、30、60的情况下,发射站变化率始终不小于0,并且最多可以减少使用16.67%的发射站。表明HPDA_REM所需发射站数目不大于UPDA_EM,由于发射站易被侦测定位和受反辐射导弹攻击,当采用较少的发射站时,有利于提高系统整体的战场生存能力。 图6 α分别取值为10、30、60时发射站变化率Fig.6 Change in number of transmitters for α=10,30,60 当γ、γ′表示接收站总数量时,由(8)式可得接收站变化率曲线,如图7所示。 图7 α分别取值为10、30、60时接收站变化率Fig.7 Change in number of receivers for α=10,30,60 由图7可知,相比于UPDA_EM,HPDA_REM所需的接收站数量有增有减。值得注意的是,当α=60时,HPDA_REM所需要的接收站数量明显增大,这是因为发射站成本远大于接收站,在协同布站时使用大量的接收站代替发射站。即使在数量上接收站和发射站一增一减,但是由于费用比α较大,从成本上看仍然降低了部署费用。 以α=60、Lmax=5 km为例说明HPDA_REM的部署结构,如图8和图9所示。图8和图9中,gn为模式Fn的数量,模式Fn、Fn0、Pml及Pmr中接收站的个数分别为n、n0、ml、mr. 图8 α=60时布置线与模式Fn的数量Fig.8 Number of deployment lines and pattern Fn for α=60 图9 α=60时模式Fn、Fn0与Pml、Pmr内接收站数量Fig.9 Number of receivers in different deployment patterns for α=60 由图8和图9可知,HPDA_REM的部署结构分为4种: 当H=14 km时,覆盖整个区域需4条布置线;每条布置线为中间3个F5模式、2个F4模式,两端均为P2模式,此时HPDA_REM的部署结构是异构且两端对称的,H分别取17 km、15 km、10 km、7 km、5 km均为该类型。 当H=8 km时,需要2条布置线覆盖整个区域。每条布置线的部署方式为中间6个F3模式、两端均是P1模式,此时HPDA_REM的部署结构属于同构且两端对称,H分别取20 km、19 km、18 km、16 km、13 km、12 km、8 km、4 km时均为此类。 当H=11 km时,需布置线3条。单条布置线的部署方式为中间5个F5模式、两端分别是模式P2与P3,此时的部署结构为同构且两端非对称。 当H=9 km时,需要3条布置线覆盖整个区域。每条布置线的部署方式为中间2个F8模式与2个F7模式、两端分别是模式P3与P4,此时HPDA_REM的部署结构属于异构且两端非对称,H分别取2 km、3 km、6 km时亦为此类。 对于确定的区域S,其宽度H已知,此时布置线数量q决定了单条栅栏的宽度2h,由(7)式可知,q同时确定了模式Fn中最大接收站数量: 以α=60情况为例说明利用引理5可以显著降低算法计算量,仿真结果如图10所示,为便于显示,记m′c=10lgmc. 图10 α=60时两种算法计算量比较Fig.10 Comparison of two algorithms calculations for α=60 由图10可知,相比UPDA_EM,本文所提HPDA_REM的计算量至少低14.53 dB,且随着区域宽度H的增加,计算量减少的幅度更明显,最大到27.53 dB. 由于当H取值变大时,UPDA_EM的布置线搜索上限明显增大,此时单条栅栏宽度变小,模式Fn内可以布置的接收站相应增多。因此UPDA_EM的计算量随着H增大会快速增大。相比而言,由引理5,HPDA_REM的布置线搜索上限随H的增加仅缓慢增加,而且由于单条布置线的宽度更大,模式Fn内可布置的接收站更少,因此随着H的增大,HPDA_REM的计算量略有下降。特别地,随着H变化,HPDA_REM的计算量呈锯齿状变化。这是因为尽管宽度H增大,但是其布置线的上限可能会不变,此时模式Fn内可布置的接收站数量随着H的增大而减少。例如,H由6 km变化到11 km,布置线数量的上限始终为6,模式内可布置的最大接收站数量分别为49、35、27、21、17、13. 当H继续增大如H=12 km时,布置线上限增大,单条栅栏宽度变小,算法计算量再次增大,因此出现锯齿峰值。 本文针对多基地雷达组网布站问题,以雷达覆盖区域为出发点提出一种新的布站优化方法。该方法通过证明异构布站模式下单条部署线的布站优化准则,进而提出基于费效比最小的优化模型。仿真实验表明,与现有同类方法相比,本文所提方法具有费效比低、发射站少,计算量小的优势,可以节约部署成本,提升战场生存概率。


2.3 布站模式Gn,m的布站优化方法
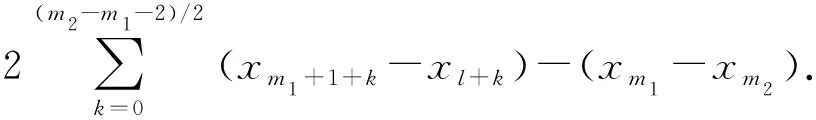
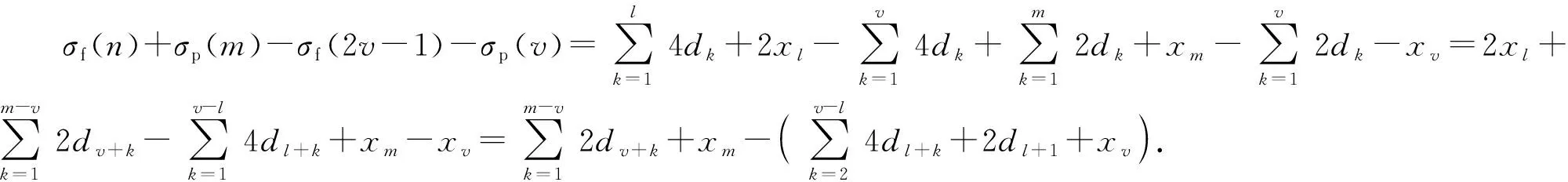
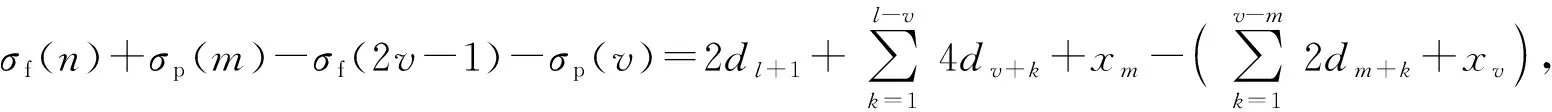
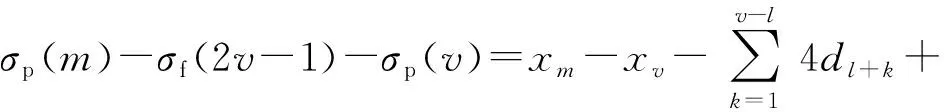
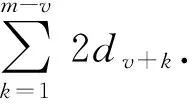
2.4 单条布置线的布站优化方法
2.5 优化模型
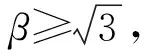

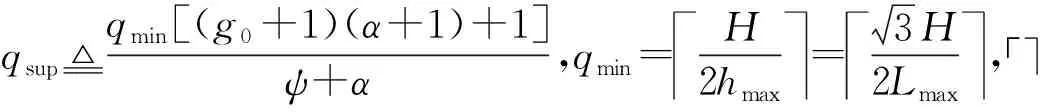
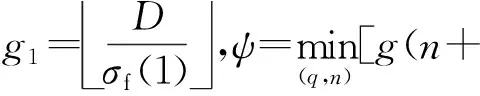
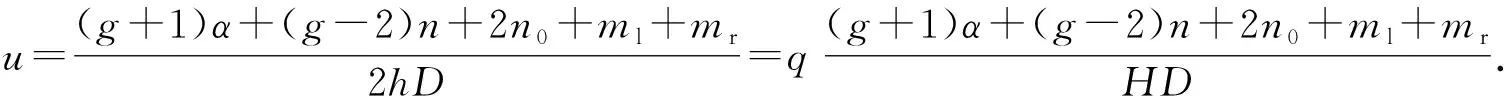
2.6 算法步骤
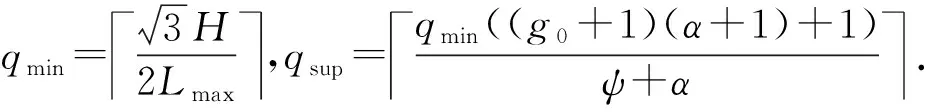
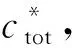
3 仿真实验
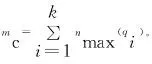

4 结论
