基于BP神经网络的潜地导弹落点参数计算方法

田春军

(江苏自动化研究所， 江苏 连云港 222061)

弹道导弹诸元准备的主要任务是根据实际发射条件计算出一条由发射点到目标点的标准弹道，并以该弹道为基准计算出一套诸元参数，装订于弹上，弹上相关系统以所装订的诸元参数为基准实施导弹的飞行控制，确保导弹实际发射后能沿着选择的弹道飞行，并以要求的精度命中目标[1]。由于潜地导弹是以潜艇为平台，水小机动发射，发射点具有不确定性[2]，发射过程在水下运动状态下完成，因此相比于陆基弹道导弹发射点、目标点基本确定的情况[2]，潜地导弹的弹道计算要求快速完成，否则弹道计算的时间间隔将使得实际发射点偏离计算发射点，而这种偏差可达数海里，严重影响导弹的落点精度。由此可见，缩短弹道计算时间，是弹道导弹从陆上发射发展到水下机动发射，必须解决的一项重要技术。目前，弹道导弹弹道快速计算是依据弹道的不同特点，分段采取相应的快速计算方法[3-8]实现，本文给出的基于BP神经网络的弹道落点参数计算方法对给定的初始计算参数直接计算出落点参数，避免了弹道的分段计算过程及弹道分段计算引起的误差积累，并通过仿真计算验证了算法的有效性。

1 六自由度弹道方程及计算方法

潜地导弹为一种大型飞行器，其空间运动除了质心的移动外，还有绕质心的转动，同时在主动段飞行过程中还受有制导控制系统的作用，因此其弹道运动微分方程主要由质心运动方程、绕质心运动方程、姿态控制方程、关机方程和导引方程、姿态角联系方程等组成[9-14]，在考虑多种实际影响因素后，某型导弹的仿真模型包含了400多个变量，由100多个微分方程以及1 000多个代数方程组成[9-10]，限于篇幅，仅列出质心运动和绕质心运动的动力学和运动学矢量方程。

潜地导弹质心运动的动力学和运动学矢量方程如式(1)所示：

(1)

潜地导弹绕质心运动的动力学和运动学矢量方程如式(2)所示：

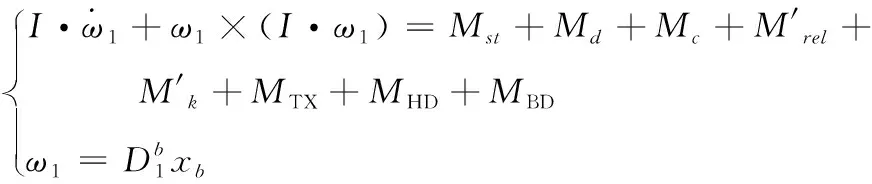
(2)

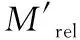
通常采用龙格-库塔、Adams预报-校正法等数值积分迭代算法计算弹道运动微分方程，在给定初始计算参数后，通过积分迭代计算，可求得落点参数。由于弹道运动微分方程组成复杂，方程中的很多系数值是以图表的方式给出，方程计算中将伴随着大量的函数插值计算，且弹道运动微分方程还是一个非线性的病态方程[11]，弹道计算迭代次数多，计算时间长[5,13]，不能满足潜地导弹变发射点机动发射的要求，因此需要弹道的快速计算。

2 BP神经网络计算落点参数可行性分析

弹道运动微分方程为变系数非齐次常微分方程，通过对弹道运动微分方程的理论分析及计算验证可知，弹道运动微分方程的初始计算参数与落点参数之间存在一一对应的关系，若将弹道运动微分方程视为一非线性系统，则其建立了初始计算参数(输入)与落点参数(输出)之间的一一对应的非线性映射关系。

BP神经网络是一种基于误差反传的多层前馈网络，是迄今为止应用最为广泛的网络，由输入层、隐层和输出层组成。BP神经网络结构简单，只要给定足够的隐层及隐节点数，其就可以逼近任意的非线性映射关系[15-17]；BP神经网络具有自适应学习的优点，为网络提供足够的训练样本供其学习和训练，便能完成由输入到输出的正确映射，识别出内部蕴含的规律；同时BP神经网络还具有容错能力和泛化能力[18]，网络训练过程中若个别样本带有较大误差或存在错误，不会影响网络给出正确映射关系，当向训练好的网络输入非样本数据时，网络能够完成映射，给出正确的输出结果。因此利用BP神经网络的非线性映射能力、自学习能力、容错能力及泛化能力，为网络提供足够的训练样本，可建立出满足精度要求的弹道导弹落点参数快速计算的神经网络模型。

3 基于BP神经网络的落点参数计算

3.1 计算变量的选择

BP神经网络输出变量选择较为容易，通常是要实现的目标。BP神经网络输入变量一般选取对输出影响大的变量，且各输入变量之间不相关或相关性小。对于导弹落点参数计算这一具体问题而言，输入变量的选取，可从两方面进行分析，一是从初始计算条件的变化对落点参数的影响程度进行定性分析，选出对落点参数影响较大的变量；二是从弹道方程变量间的内在关系进行定性分析，选出在本质上对落点参数有影响的变量，最后统筹考虑上述两方面的结果，最终选出合适的输入变量。

3.1.1初始计算条件对落点参数的影响分析

弹道运动微分方程的输入多达上百项，在给出初始计算参数后，计算弹道运动微分方程可求出落点经纬度参数(λc,Bc)。虽然完整的输入变量多达上百项，但在BP神经网络的学习训练过程中，这些输入变量的地位和作用是不平等的，有些初始输入变量对落点参数有直接显著影响，有些对落点参数产生间接影响，有些没有影响。

由发射坐标系[12]的定义并结合弹道运动微分方程，可将初始计算参数对落点参数的影响，分为三类：一类为初始计算参数不随发射点或落点的改变而改变，如发射点在发射坐标系中的位置分量(x0,y0,z0)，计算初始值均为0；俯仰、偏航、滚动3个姿态角分量初始值为固定取值φ=90°，ψ=0，γ=0，这些变量作为初始输入是常量，在BP神经网络的逼近中认为对落点没有影响，这类变量不需考虑；二类为随着发射点、目标点的不同而改变，如发射点纬度B0，发射方位角A0，关机时间tk等，在BP神经网络逼近中需充分考虑；三类为一些特殊的初始计算条件，需结合具体的样本设计进行选择，决定是否在BP神经网络的逼近中考虑，如发射点经度λ0，由于弹道运动微分方程在建模时所选地球模型为轴对称的旋转椭球体，对于一组确定的发射点和落点，发射点经度改变Δλ，落点经度同样的改变Δλ。

3.1.2变量内在关系对落点参数的影响分析

对式(1)进行如下分析[19]：

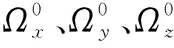
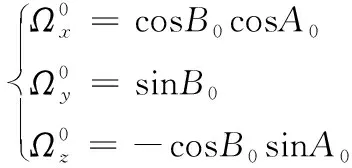
(3)

3.2 样本数据设计和BP神经网络结构设计

通常映射关系越复杂，所需样本数据越多，样本的选择要有代表性和均衡性，针对所研究的问题，采用如下方式进行样本设计：

1) 由于地球为旋转椭球体，固定发射点经度为λ0=0；

2) 发射方位角区间为[0,360°)，间隔取5°；

3) 确定导弹发射纬度范围[-70°,70°]，发射点纬度取值间隔为10°；

4) 关机时间区间[237.0,367.0]，取值间隔为5 s。

将以上4点进行组合，为发射点样本，通过弹道运动微分方程计算生成落点样本数据，选取部分数据作为测试样本数据，其他为训练样本数据。

根据样本数据的特点，通常将样本数据进行归一化处理，将样本数据限制在[-1,1]区间内，采用下式：

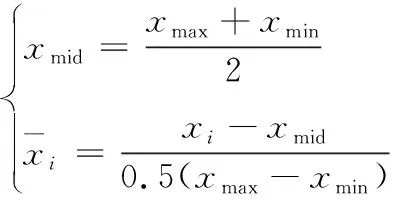
(4)

式(4)中：xi为样本数据；xmin为样本数据最小值；xmax为样本数据最大值；xmid为样本数据中间值。

按式(4)进行归一化后，处于中间值的样本数据为零，样本数据最大值和最小值分别为1和-1。

BP神经网络的结构设计主要是隐层数和隐节点数的设计。通常一个3层的BP神经网络已经具有了非常强的逼近能力，因此仅设计一个隐层。确定隐节点数通常采用试凑法，即先设置较少的隐节点训练网络，然后逐渐增加隐节点，用同一训练样本训练，从中确定出网络误差最小时对应的隐节点数，经过大量的仿真试验，隐节点数确定为120。最终所确定的三层BP神经网络的结构为3-120-2，即3输入、120隐节点、2输出。

3.3 BP神经网络训练算法及转移函数

标准BP神经网络采用梯度下降算法，反向传播计算梯度，但其存在自身的不足，样本较多时训练时间长，易收敛于局部极小值等。目前已经提出了很多改进算法，如附加动量法、共轭梯度法、拟牛顿法、自适应学习速率法、Levenberg-Marquardt方法等。多数情况下，建议使用Levenberg-Marquardt方法。

利用BP神经网络解决实际问题时，除了训练算法的选取很重要外，转移函数的选取也很重要,主要有3种转移函数：单极性sigmoid函数、双极性sigmoid函数、线性函数。

单极性sigmoid函数：

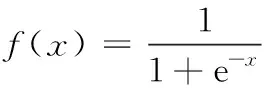
(5)

双极性sigmoid函：

(6)

线性函数：

f(x)=x

(7)

隐层和输出层的转移函数对BP神经网络的预测精度有较大影响，通常隐层转移函数选用单极性sigmoid函数或双极性sigmoid函，输出层转移函数选用线性函数。

BP神经网络训练时，最大训练次数epoch可根据网络规模、样本量等确定，经仿真试验，设定epoch数为1 600；网络训练要求的精度goal为0；损失函数一般为均方差MSE，如下式：

(8)

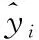
4 仿真计算与结果分析

图1、图2分别表示落点纬度、落点经度差训练数据计算误差，落点纬度、落点经度差训练数据均为28 285组；图3、图4分别为落点纬度、落点经度差测试数据计算误差图，落点纬度、落点经度差测试数据均为875组。

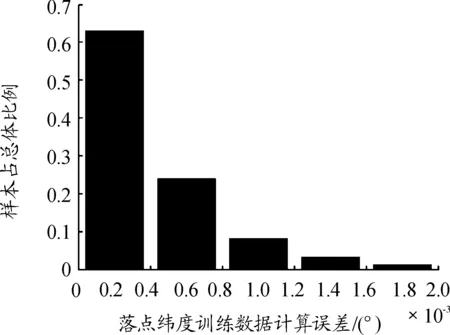
图1 落点纬度训练数据计算误差直方图

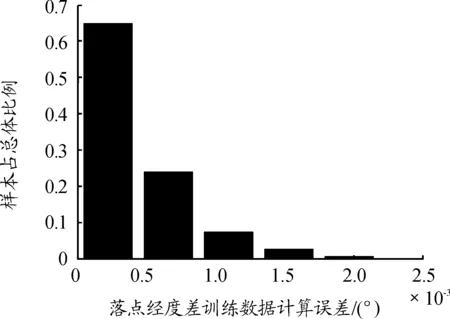
图2 落点经度差训练数据计算误差直方图

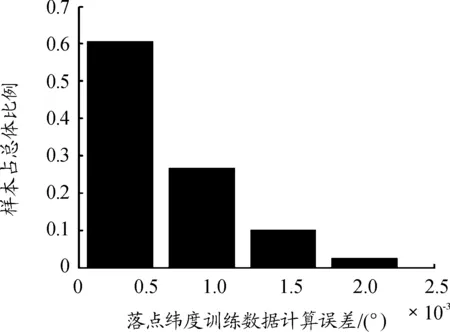
图3 落点纬度测试数据计算误差直方图

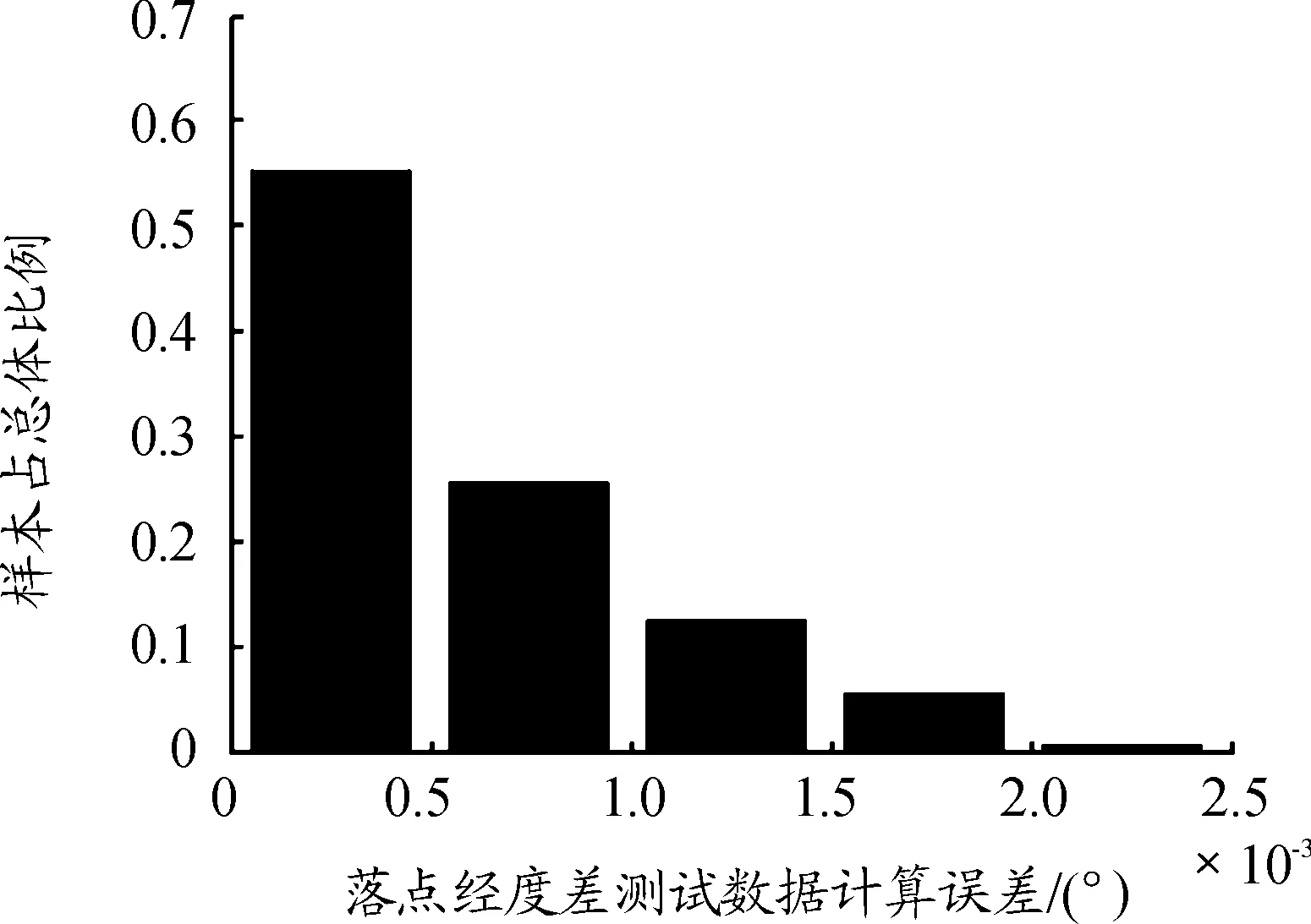
图4 落点经度差测试数据计算误差直方图

由图1～图4计算误差直方图可知，BP神经网络对落点纬度的训练，约95%的训练样本计算误差落入区间(0,0.001°)；BP神经网络对落点经度差的训练，约96%的训练样本计算误差落入区间(0,0.001°)；BP神经网络对落点纬度的测试，约87%的测试样本计算误差落入区间 (0,0.001°)；BP神经网络对落点经度差的测试，约81%的测试样本计算误差落入区间(0,0.001°)，且全部训练、测试样本计算误差均未超过10-3的量级。因此BP神经网络正确识别出了所研究问题内部蕴含的规律，且所建立的落点参数计算模型具有非常好泛化能力，向落点参数计算模型输入初始计算参数后，可给出满足精度要求的落点参数。

表1为BP神经网络对落点纬度训练数据、测试数据误差统计结果；表2为BP神经网络对落点经度差训练数据、测试数据误差统计结果。

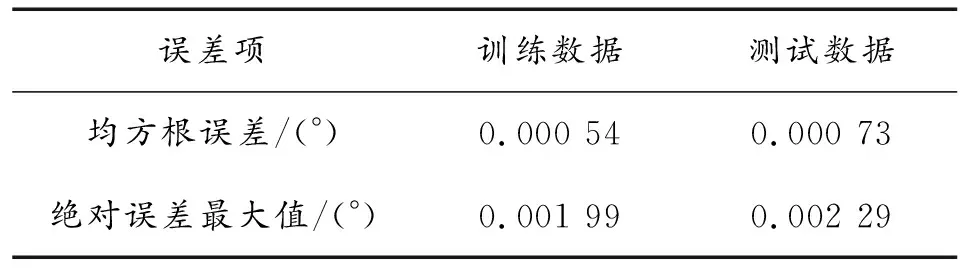
表1 落点纬度误差

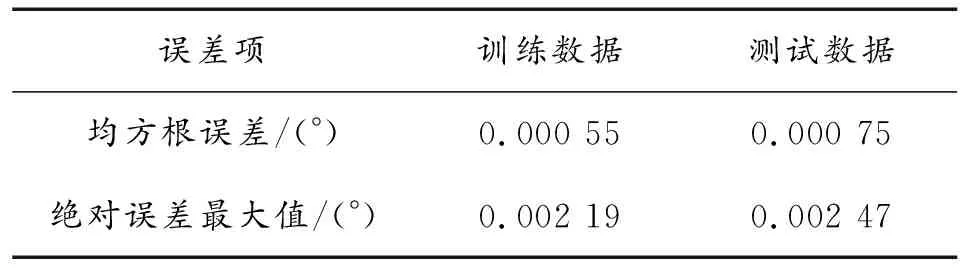
表2 落点经度差误差

由仿真计算结果可知：基于BP神经网络的导弹落点参数计算方法计算误差非常小，以地球平均半径R=6 371 004.0 m进行计算，落点纬度训练样本均方根误差为59.8 m，测试样本均方根误差为81.5 m；落点经度差训练样本均方根误差为61.1 m，测试集均方根误差为83.2 m，与数值积分迭代计算弹道微分方程相比较，计算精度相差不大，能够满足使用要求，但计算量很小，计算一组落点参数在PIII 500计算机上的计算时间小于0.01 s，因此所建立的计算模型有效。

5 结论

本文基于BP神经网络的潜地导弹落点参数计算方法，对给定的初始计算参数可直接计算出落点参数，仿真计算结果表明，计算精度较高，能够满足使用要求，由于弹道运动微分方程不进行数值积分迭代计算，极大的提高了落点参数的计算速度。本文算法可为实现潜地导弹水下变发射点机动发射提供技术支持。