路面激励对火箭炮行进间发射控制的影响研究
2021-05-06孙志群曾正森李世康
孙志群,李 强,袁 卫,曾正森,李世康
(1.中北大学 机电工程学院, 太原 030051; 2.重庆长安工业有限责任公司, 重庆 400000)
火箭炮是一种大面积杀伤武器,配合制导弹药,已经使行进间发射成为可能,提高行进间发生调炮精度成为重中之重。车载火箭炮的行进间发射大大提高了武器系统的作战效能,但在武器系统行进时,车体随着路面的起伏而振动,严重影响火箭炮的射击精度。行进间发射涉及地面力学、车辆动力学及发射动力学[1],其各个学科的耦合对于火箭炮的调炮控制提出了更高的要求。目前对于调炮控制的研究较多,但主要侧重于控制方法的研究,文献[2-3]应用滑模控制和PID控制方式对火箭炮固定发射调炮控制进行研究,未考虑实际系统的动力学模型。事实上,火箭炮发射过程中,受到冲击载荷后整个系统发生振动,对于作动器的干扰不能忽略,行进间发射路面颠簸形成的干扰会对控制精度产生影响,随着防空武器精度要求的提高,这一差异逐渐凸显,不容忽视。
由于火箭炮行进间发射要求较高,目前对于火箭炮行进间发射的研究较少,但坦克行进间发射已有众多研究。金涛等[4]通过建立坦克多刚体模型,采用 PID(proportion integration differentiation) 控制对坦克火炮进行控制,说明了在坦克高速行驶时,PID控制依然能较好控制火炮。史力晨、陈宇等[5-6]通过状态方程法建立了坦克、火炮系统的振动模型,将系统的动力学响应看作了多刚体系统对地面不平度激励的响应问题,稳定器作用通过刚性系数体现,计算分析了坦克行进间火炮运动规律;但车载火箭炮系统重量较坦克轻,采用轮胎行进的方式对路面状况更为敏感,须对其行进间发射控制性能单独研究。
本文拟采用机电耦合方法研究火箭炮行进间发射中,路面不平度对于PID控制的影响,首先利用Adams基于拉格朗日方程建立车载火箭炮系统的动力学模型,并利用谐波叠加法建立三种代表性路面不平度,最后通过Matlab/Simulink建立大功率伺服电机控制模型,联合仿真计算火箭炮行进间发射PID控制的有效性,并给出路面不平度对控制精度的影响。
1 车载火箭炮系统动力学模型
本文模型为6×6轮式底盘、箱式多管火箭炮系统。动力学模型分为两部分:运载车体和火箭炮发射系统。车体包括车轮、悬架、车架;发射部分包括高低机、方向机及发射箱。
1.1 车体部分建模
车体动力学模型在Adams/View环境下构建。轮胎是车辆至关重要的部分,起到驱动车体行进、支撑车体、抑制路面不平度引起的振动与冲击的作用。因此,轮胎模型对整体仿真产生很大影响,Adams中提供了多种轮胎模型用于不同车辆的仿真计算。本文计算内容主要考虑车体直线运动时车体振动,不涉及车辆平顺性及耐久性分析,因此选择采用UA轮胎模型。设置轮胎半径0.75 m;轮胎断面宽度0.40 m;径向刚度870 N/mm;径向阻尼80 N·s/mm。设置轮胎6轮驱动,直线行驶速度50 km/h。
车体悬架与车体连接位置、方式及自身尺寸参数影响车辆振动特性,所以采用原车悬架设计尺寸及连接方式,减震器用弹簧代替,设置弹簧刚度1 000 N/mm,阻尼112 N·s/mm。悬架具体结构如图1所示。

图1 车辆悬架
1.2 发射部分动力学模型
发射部分底座与车体做固定铰连接;方向机与底座设置旋转铰连接;发射箱绕高低机轴旋转;左右发射箱各20发火箭弹,且火箭弹与定向器碰撞接触。
接触碰撞通常采用非线性弹簧-阻尼模型进行计算,两物体发生碰撞的判断条件为是否产生穿透,当穿透量小于零时,两物体间的碰撞力零,否则碰撞力正。碰撞力的定义[7]如下:
(1)
式中:k为碰撞表面的刚度;e为弹性系数;δi为穿透力量;cmax为最大阻尼系数;δmax为最大穿透量。可由以Hertz定律为理论基础的刚度计算公式给出。
在确定的控制方式下,火箭炮行进间发射调炮精度主要受路面激励及火箭弹燃气流冲击的影响,对这两部分载荷的施加至关重要。关于路面激励的施加,将在后面章节给出。通过实验得到火箭弹燃气射流对定向管X、Y、Z方向的冲击力,其力值随时间变化情况如图2所示。
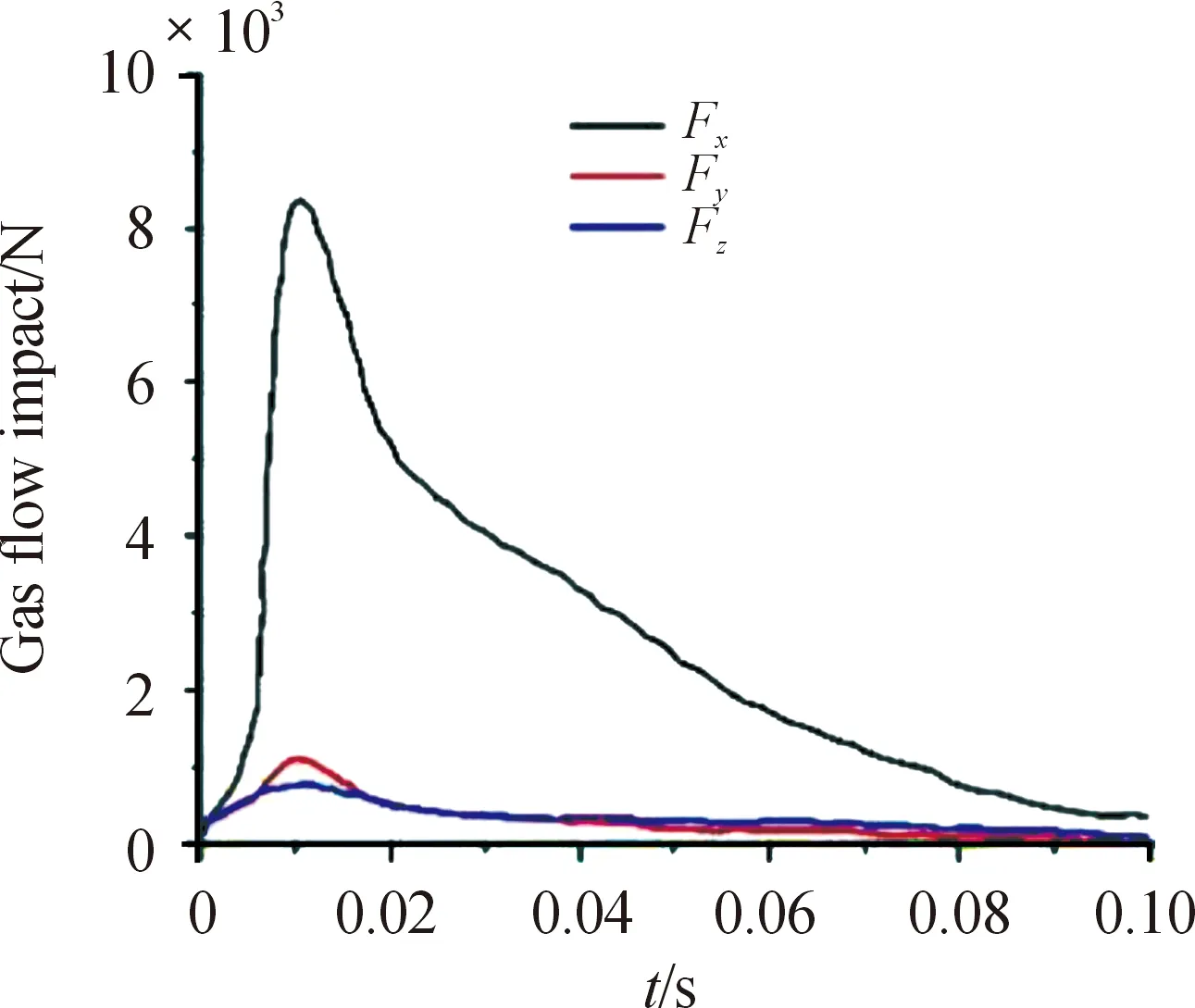
图2 火箭弹燃气流冲击力曲线
2 路面谱建立
2.1 谐波叠加原理
国际标准化组织(ISO)和我国国标GB/T7031—2005均采用下式功率谱密度函数拟合[8]:
(2)
式中:n为空间频率;为波长λ的倒数,表示每米长度中包括几个波长;n0为参考空间频率n0=m-1;Gq(n0)为路面不平度系数,它是参考频率n0下的路面功率谱密度;W为频率指数-双对数坐标上的斜线斜率,决定着路面功率谱密度的频率结构,一般取2。
按照Gq(n0)的不同可以将路面分为A~H 8个等级(表1),值越大,表明路面不平度越大,对车辆振动影响越大。

表1 路面不平度参数
式(2)是基于空间频率的表达式,由车速和时间频率之间的关系可以写出时域下的表达式[9]:
f=vn
(3)
(4)
其中:f为时间频率(Hz);v为车速(m/s)。路面不平度的方差可以表示为:
(5)
将f划分为N个小区间,用每个区间的中心频率fi处的谱密度值Gq(fi)代替Gq(f)在小区间内的值,则:
(6)
其中:δf=(fl-fu)/N。则每个小区间的路面不平度幅值:
(7)
那么用标准差为Ai的正弦波函数表示每个区间的路面模型为:
(8)
其中θi为区间[0,2π]内的随机数。最后将小区间的正弦波叠加在一起,得到时域内随机路面不平度模型:
(9)
转换为空间域内的表达式为:
(10)
由于汽车振动系统的固有频率在0.7~15 Hz,常用车速为36~180 km/h(10~50 m/s)[10],取地面作用于轮胎的激励时间频率下限为fl=0.5 Hz、上限为fu=30 Hz则研究车辆振动时需要的空间频率上、下限分别为:
(11)
(12)
由式(11)(12)可知,在0.01~3 m-1的空间频率内模拟路面不平度,便可覆盖车辆系统的固有频率,从而保证由谐波叠加法所得的路面不平度作为激励,车辆振动情况结论符合实际情况。
由奈奎斯特采样定理:采样频率ns≥2nu,采样间隔Δx、Δy必须满足
由此Δx≤0.166 7 m, Δy≤0.166 7 m,本文取Δx=0.1 m。
2.2 路面谱实现及应用
基于谐波叠加法编写Matlab算法,生成A级、D级、F级3种路面不平度路面,其三维路面谱如图3~图5所示。
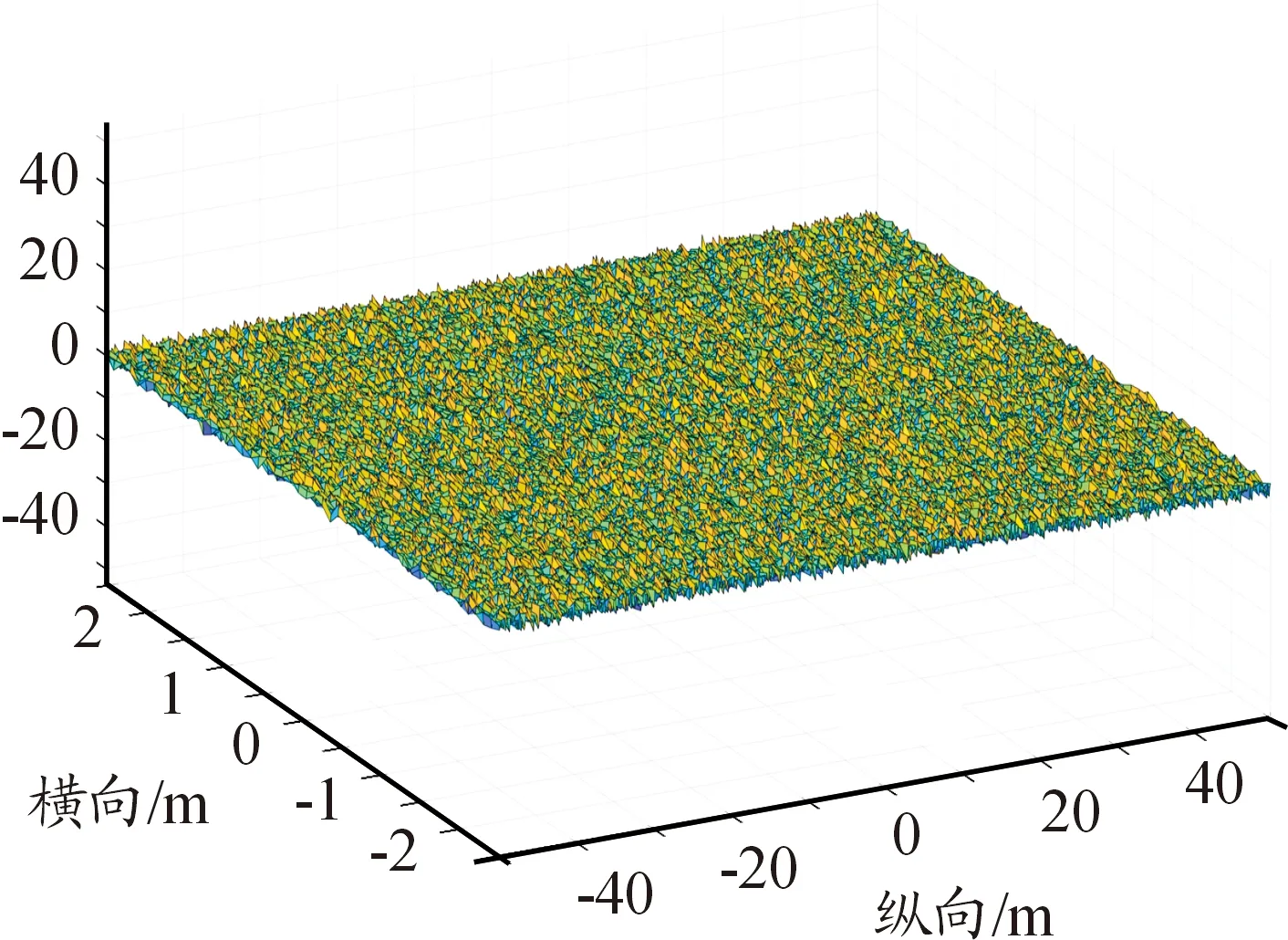
图3 A级路面谱

图4 D级路面谱
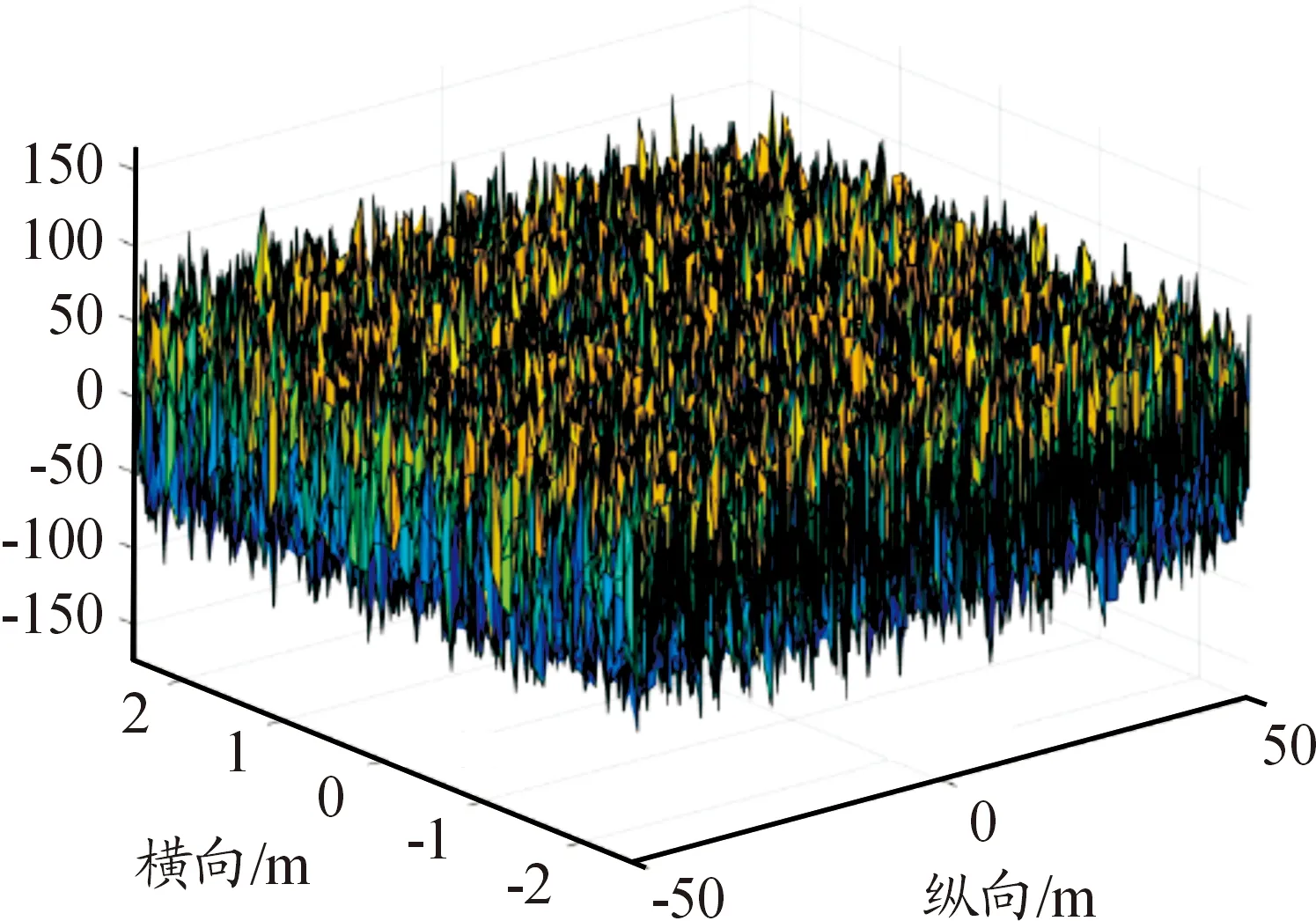
图5 F级路面谱
3 机电联合建模
伺服电机具有效率高、功率密度密集以及易于控制的优点,本文研究的火箭炮系统以伺服电机为执行机构。火箭炮在瞄准过程中,发射箱的调炮过程及对打击目标的动态跟踪全部依托于位置伺服系统。火控计算机给出目标方位指令,并将其发送给驱动计算机,继而计算伺服电机相应的模拟电压量,实现动态跟踪。伺服电机的控制采用电流-速度-位置三闭环控制。
PID控制结构简单,算法简单易懂,参数含义明确,具有较好的鲁棒性,并且对于精确模型的要求低,所以在实际工程中,是一种应用最为广泛的控制算法。
假设多管火箭炮俯仰和回转机构的指令角度为qd=[θdφd]T,则误差为:
e=qd-q
根据PID控制律,则多管火箭炮俯仰、回转控制器设计为:
式中:Kp为比例系数;Ki为积分时间常数的倒数;Kd为微分时间常数。在Matlab/Simulink中建立PID控制模块,并将Adams中的动力学模块联合,联合仿真系统模型如图6所示。

图6 联合仿真系统模型框图
4 仿真与分析
本文针对行进间发射过程中不同路面不平度对PID控制的影响进行研究。将车载火箭炮行驶速度设置为50 km/h,火箭炮位置伺服系统由0°调炮至1 rad,需满足如表2所示指标,分别计算A、D、F级路面行进间发射时,不同的路面等级对PID控制的影响。由于车辆前0.5 s为加速过程,本文在0.5 s之后车辆匀速运行时,给定角度指令信号,并在3 s时发射一枚火箭弹。仿真过程中采用四阶龙格库塔数值积分方法,仿真时间步长0.000 1 s,通过实验凑试法,PID参数已达最优。图7~图11为车载火箭炮在不同路面等级下PID控制俯仰角度值。

表2 火箭炮伺服系统性能指标
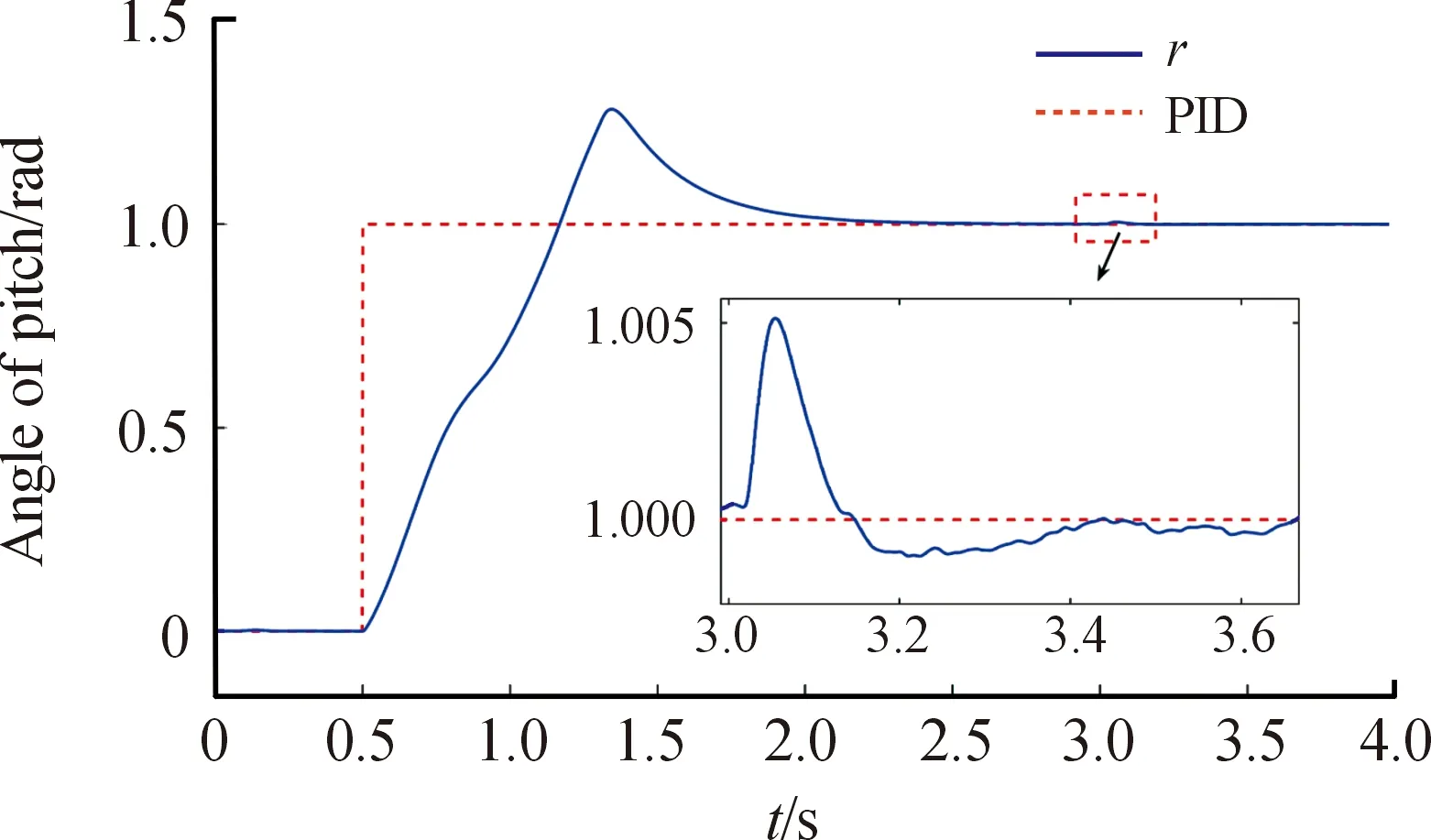
图7 A级路面高低角变化曲线

图8 A级路面平稳运行高低角变化曲线

图9 D级路面高低角变化曲线
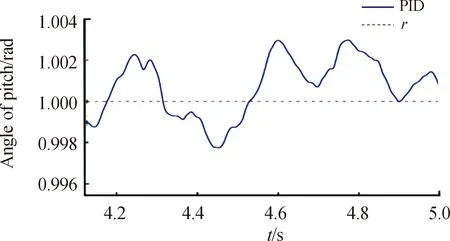
图10 D级路面平稳运行高低角变化曲线

图11 F级路面高低角变化曲线
从图7、图8可以看出在A级路面行进间发射,PID控制方式可以得到良好的控制精度。由于火箭弹燃气流冲击造成的扰动为4.78 mil,且在0.4 s内恢复到指定角度;由路面不平度造成的扰动最大为0.95 mil,满足性能指标要求。由图9~图11可以看出,随着路面不平度的增大,PID控制精度下降。其中D、F级路面下按照50 km/h的速度行进,俯仰角度最大控制误差分别为2.89 mil、9.55 mil。通过表3表明,PID控制下为了同时兼顾快速性和稳定性,在实际的控制过程中出现超调,且随着路面不平度的增大,超调量增大,调节时间增长。
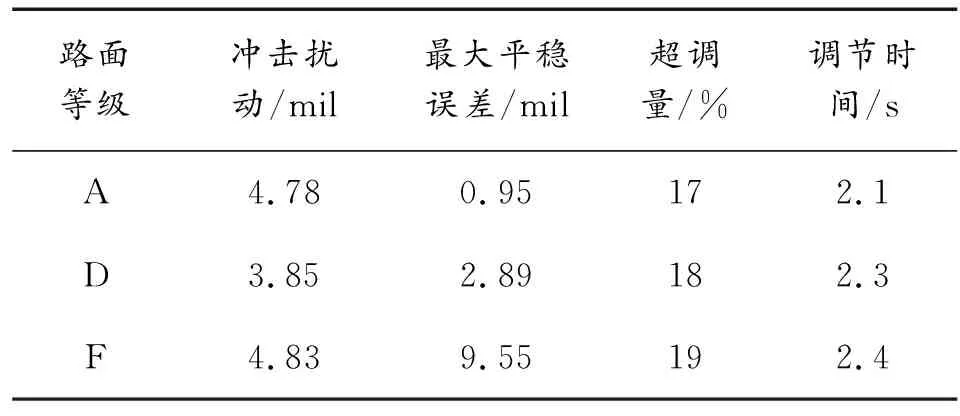
表3 不同等级路面下各参数对比
5 结论
1) PID控制作为一种经典的控制方式,在激励较小的A级路面可以达到精确的控制效果,但其控制精度随着路面不平度的增大而降低,验证了火箭炮在优质工况下行进间发射的可行性。
2) PID控制为了兼顾快速性和稳定性会出现超调,且超调量随路面不平度的增大而增大。
