基于传输线拐角的区域分解有限元相减法
2021-05-05樊宽刚陈仁义邱海云
樊宽刚,陈仁义,何 兵,邱海云
(1.江西理工大学 电气工程和自动化学院,赣州 341000;2.江西理工大学 机电工程学院,赣州 341000)
0 引言
随着电子设备小型化以及电路中5G信号频率快速增加[1~3],电子控制系统的传输速率和时钟频率在不断的上升和提高。现在的时钟频率从原来的几十MHz上升到几GHz,信号的转换时间从纳秒级变为皮秒级,时钟及总线频率快速上升,信号上升边沿极速变陡,从而导致PCB上的信号走线对电子控制系统的性能造成极大的影响。当电子控制系统处于低频(几十MHz)时,PCB上的信号走线对信号传输影响不大;当电子控制系统处于高频(大于几十MHz)时,就必须考虑信号走线上面的传输效应[4,5]。信号会流经芯片内部、BGA封装、焊盘、过孔、拐角、间隙等任何传输结构,这些传输路径都会产生传导和辐射等相关问题[6,7]。高速互连线之间的布线走线、元器件和元器件之间的布局连线也会产生相同的问题,因此研究传输线互连结构有助于电子产品的设计[8]。
文献[9,10]以及文献[11]分别从两方面对传输线结构进行研究分析。一方面是在理论上对传输线S参数进行理论分析,得到适合于自身模型的S参数公式。另一方面从传输线物理结构出发,通过改变传输线的模型结构,得到传输性能更好的传输线结构模型。但上述文献并没有把提取S参数法与传输线结构相结合进行详细阐述。
针对上述情况,本文提出了一种区域分解的有限元相减法,通过ANSYS HFSS对传输线结构进行了仿真验证及路径优化,实验测试验证了算法和仿真模型的正确性。
本文创新点如下:1)提出了一种区域分解的有限元相减法,提高了计算精度;2)提出了一种半圆弧拐角结构,经仿真及实验测试表明能有效降低传输线拐角辐射11.2%。
1 传输线算法研究
1.1 拐角处S参数提取法
假设不连续处的传输线在空间中处于无限长,便可以通过有限元理论计算得到准确的S参数值。但在实际中,传输线有限长,只能通过传输线端接负载的方法来模拟无限长传输线。一般情况下该方法可行,但是对于传输线拐角处微小的匹配失调都对S参数的计算造成极大的误差[12]。针对上述情况,本文提出一种拐角S参数相差法来提取拐角处S参数值。

图1 传输线辐射场示意图
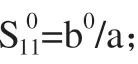
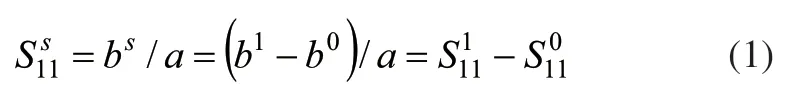
1.2 区域分解的S参数计算
1.2.1 PCB板电源/地平面的有限元算法
电源/地平面厚度与信号波长相比非常小,电源/地平面的z方向上只有Ez分量,在xy水平面上只有磁场分量Hx和Hy,以Ez为主分量的二维数值模型的控制微分方程如式(2)所示。

式中,k0为自由空间的波数;εr、μr分别为PCB板介质层的相对介电常数和相对磁导率。
由于PCB四周表面是开路边界且表面电流密度为0,因此可推断出PCB四周为理想磁导体边界条件,即电源/地平面上的过孔边界条件如式(3)所示。
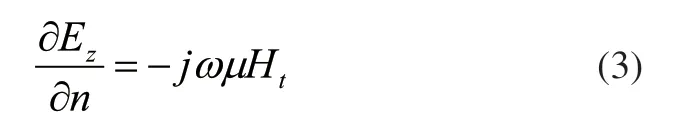
式中,Ht为切向磁场。
1.2.1 PCB板过孔区有限元算法


其中r为物理模型到柱坐标原点的距离,θ为模型投影到xy平面距x轴的角度。
在方程(4)中,令1/r和εrμr/r是与媒质有关的系数。对方程(4)的值作式(5)变换。

对方程(4)进行直角变换得方程(6)。

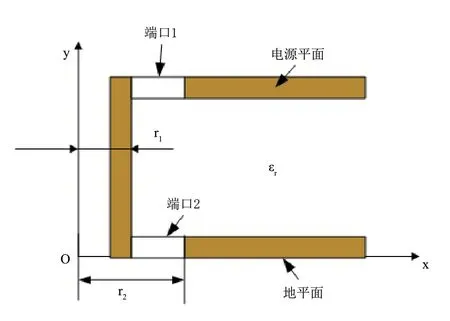
图2 过孔区的2D轴对称计算模型

设端口2为匹配边界,无反射波,只有入射波,则总场可表示为方程(8)。
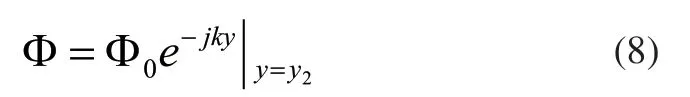
由于端口1外法线方向与纵坐标正向相同,所以边界条件如方程(9)所示。
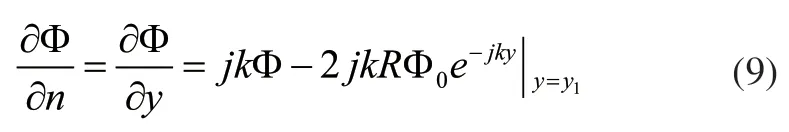
端口2外法线方向与纵坐标正向相反,所以边界条件如方程(10)所示。

代入数据求得数值模型总场分布后,可得到端口输入和输出的S参数,如式(11)所示。

通过把传输线拐角处的S参数提取法和PCB板过孔连接处的S参数计算方法相结合得到式(12),该方法能够有效提高PCB板传输线拐角S参数的计算精度,确保计算模型的准确性。
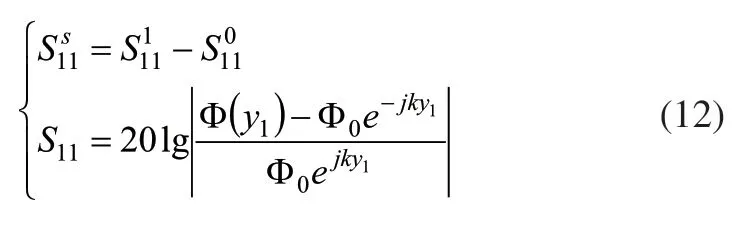
2 模型仿真及路径优化
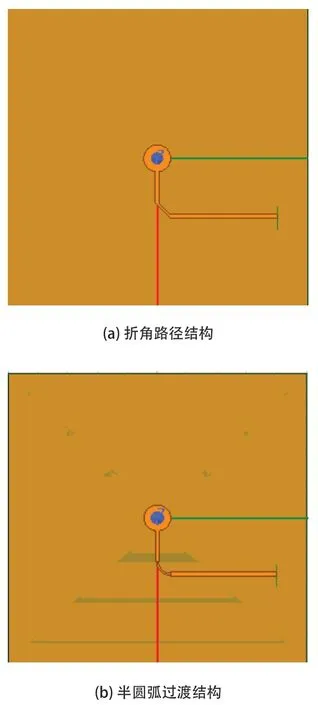
图3 传输线路径弯曲结构
传输线的连接结构仿真模型如图3所示,每个模型都是八层板模型,介质层采用FR4填充,八层板布有传输线和过孔结构,根据传输线的不同,模型可分为:折角拐角走线模型和半圆弧拐角走线模型,具体的模型参数如表1所示。在模型中,两种模型的不同之处在于表层传输线的拐角连接结构不同,其它参数都相同,以此来探讨拐角对信号传输所造成的影响。
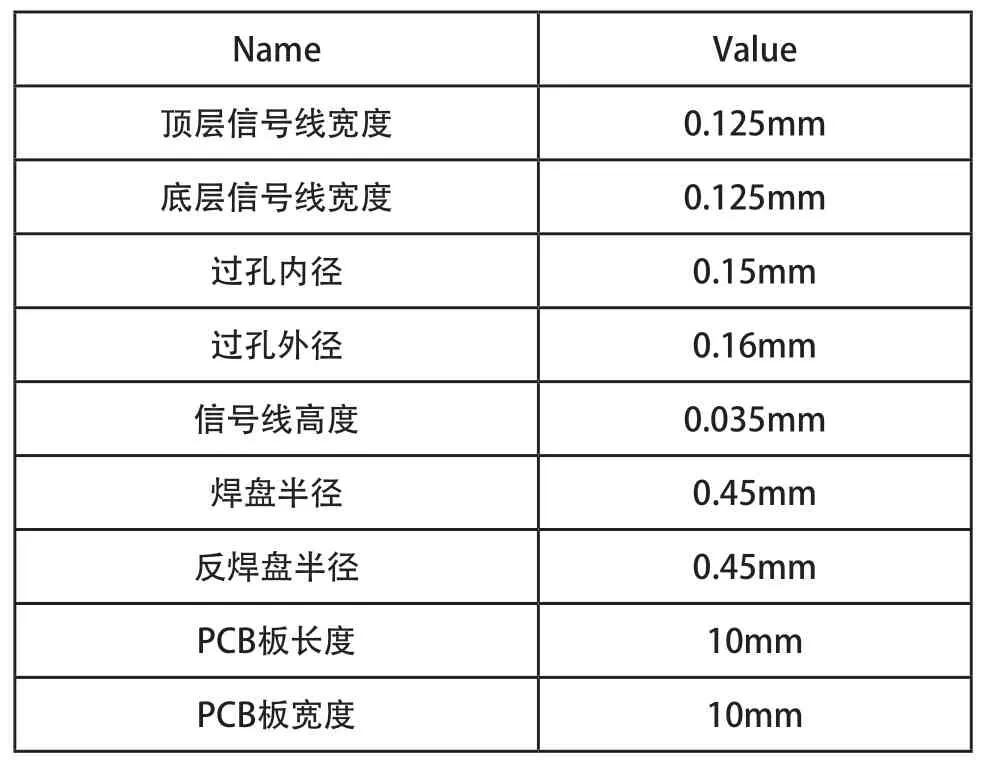
表1 传输线物理结构参数
通过ANSYS HFSS仿真得到图4,方形线代表折角路径结构,圆形线代表半圆弧过渡结构,三角形线代表区域分解的有限元相减法曲线。以S参数为参考标准,S11曲线相差较大,以3.8GHz为分界线,在3.8GHz之前,折角结构最大优于半圆弧结构0.8dB左右;在3.8GHz之后,半圆弧结构最大优于折角结构2.4dB。从总体上来看,半圆弧结构反射效应比折角结构减少11.2%左右。由图5和图6可知,折角结构最大辐射强度为0.035A/m,而半圆弧结构最大辐射为0.025A/m,由此看来,半圆弧结构整体优于折角结构。通过对有限元算法曲线和折角结构曲线进行计算分析,相关系数为0.8848,因此,两者曲线整体相似,也验证了算法的有效性。
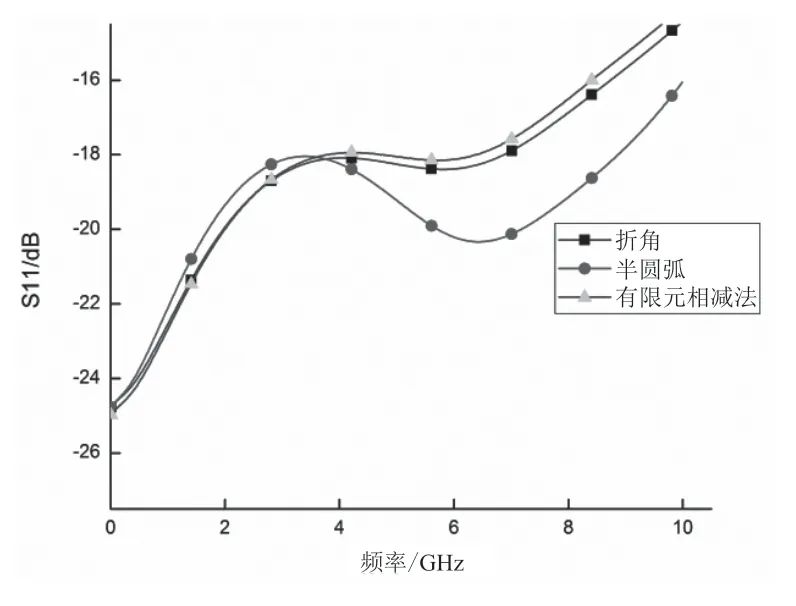
图4 仿真S参数曲线图

图5 折角拐角辐射场图

图6 半圆弧拐角辐射场图
3 实验测试
3.1 实验装置
实验装置如图7所示,主要包括三大部分:网络分析仪、传感器探头以及开发板。

图7 实验装置
在实验测试中,利用传感器探头对开发板进行探头测试,最终通过网络分析仪显示S参数曲线。传感器测试系统如图8所示,传感器测试系统通过激励源产生满足测试要求的激励信号。激励信号通过功率分配开关分为两路,一路直接进入参考接收机作参考信号,另一路进入被测件作为测试信号。测试信号经过被测件后会发生反射,通过传感定向耦合器把反射信号分离出来并送入测量接收机内,最后参考接收机和测量接收机接收的信号通过信号处理单元进行数据分析处理,显示一组S参数曲线图。
3.2 实验测试
通过传感器测试系统对开发板的折角拐角和半圆弧拐角进行实物仿真测试,分别对两模型采集500个数据进行绘图分析,测试结果如图9、图10所示。

图8 传感器测试系统
从图9和图10可以看出仿真曲线与测试曲线整体趋势非常相似,仿真结果与测试结果相差不大,说明了传感器测试系统具有较高的准确性,也验证了所建模型的正确性。

图9 折角拐角测试曲线对比图
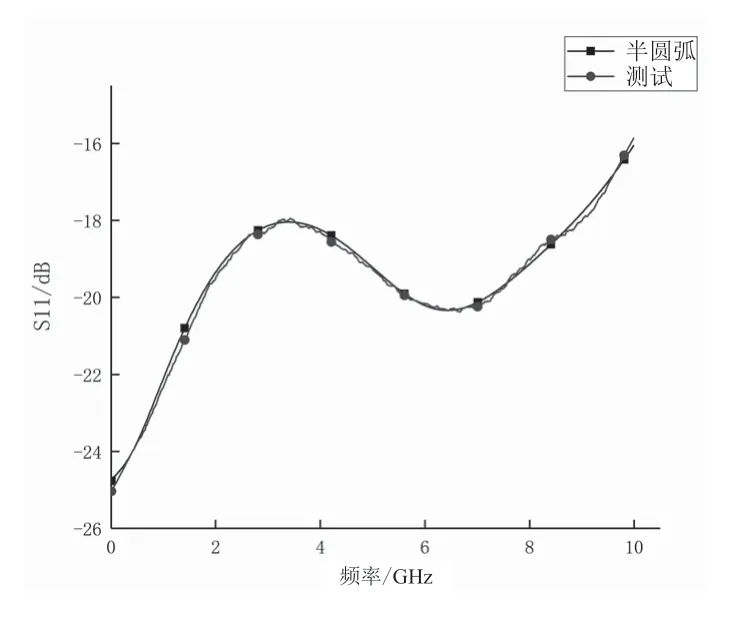
图10 半圆弧测试曲线对比图
4 结语
本文对传输线拐角进行物理建模,采用Ansys HFSS对物理模型进行仿真测试,通过传感器测试系统对所建模型进行了验证,得出以下结论:
1)针对传输线拐角问题,提出了一种区域分解的有限元相减法,仿真测试验证了该方法的有效性。
2)针对传统折角拐角传输线结构在高频信号传输过程中存在信号传输不完整问题,提出一种新的半圆弧拐角结构,仿真及实验表明该半圆弧比折角拐角结构反射效应降低11.2%。实验测试验证了仿真结果的准确性。
3)为今后5G高频信号下的PCB板传输线结构的选取提供理论基础和实验依据。
