基于自适应二进制灰狼算法的节点协同跟踪

王 珂，江潇潇，王永琦，江玉洁

（1.上海工程技术大学 电子电气工程学院，松江 201620；2.上海第二工业大学 计算机与信息工程学院，上海 201209）

0 引言

近年来，随着相关技术的发展，传感器的生产和部署成本逐渐降低，越来越多的学者聚焦于大规模传感器网络的理论和实践研究[1,2]，目标跟踪就是其中一个重要的研究方向[3]。在大规模传感器网络中进行目标跟踪时，部署的传感器数量通常大于进行数据处理时需要的节点数量，另外，全部节点之间数据传输也会加快电池能量消耗，降低网络寿命[4]。为了解决上述问题，需要在保证跟踪精度的情况下，在特定的时间间隔内选择一组最优的传感器节点参与跟踪。

近年来，众多学者针对传感器节点选择问题提出很多解决方法和模型，如基于信息论的方法，即熵[5]，相对熵[6]，以及瑞利散度[7]等，基于信息论的方法一般是通过最大化信息增益来选择传感器节点，这种方法存在的问题是其计算复杂度太高，尤其是在每个时间节点激活的传感器数目较大时。还有一种方法是基于后验克拉美罗下界（Posterior Cramer-Rao Lower Bounds，PCRLB）[8]进行求解，PCRLB是一个重要的工具，它对贝叶斯框架下的任何非线性滤波问题的状态估计提供了理论上的均方误差（mean squareed error，MSE）界限。L.Zuo等[9]提出了条件后验克拉美罗下界（Conditional Posterior Cramer-Rao Lower Bounds，CPCRLB），它基于真实的量测信息给出了比PCRLB更准确和有效的均方误差界限，更加适合于无线传感器网络的传感器节点管理。杨小军[10]等人采用穷举的方法解决节点选择问题。魏声云[11]等人采用二进制粒子群优化算法进行求解。但是以上算法在处理大规模传感器网络时，都存在收敛速度慢，容易陷入局部最优的问题。灰狼算法（Grey Wolf optimizition，GWO）[12]是Mirjalili等于2014年提出的一种群智能优化算法。

本文基于CPCRLB和自适应二进制灰狼优化算法解决WSN中目标跟踪时的节点选择问题，本文的贡献在于提出了一种自适应二进制灰狼优化算法，其采用自适应收敛因子，提高了算法的全局搜索能力，平衡了算法的探索和开发两个过程。同时，其采用V型函数的位置更新原则，加快了算法的收敛速度和局部寻优能力。最后将其应用于基于CPCRLB节点选择优化模型的求解，并在获得节点子集以后采用粒子滤波器目标跟踪，大量的仿真结果证明了该算法在处理大规模无线传感器网络目标跟踪中节点选择问题的有效性。

1 节点选择模型建立

1.1 目标状态方程和传感器节点量测方程

1）状态方程

其中，Fk为状态转移矩阵，Wk为过程噪声且为高斯白噪声，其协方差矩阵为Q。

2）量测方程

1.2 基于CPCRLB的节点选择模型

CPCRLB可以作为一个解决传感网中目标跟踪时节点选择问题的解决方案，它是费歇尔信息矩阵（Fisher information matrix，FIM）的逆，可以表示当前选择的传感器节点的跟踪性能的下界[9]。CPCRLB越小，说明当前选择的传感器节点的跟踪性能越好。

假设xˆ为x的估计值，用x0:k和z1:k表示从0到k时刻的目标状态和量测，已知初始的联合概率密度p（x0），以及噪声模型Wk和vk，其中两个噪声相互独立。

在传统的无条件PCRLB中，x0:k和z1:k都是随机向量，边界是通过对所有的z1:k和x0:k取平均值。实际上，在k+1时刻，除了目标状态方程和量测方程之外，还可能知道z1:k。在已知过去所有z1:k的条件下，当新的量测zk+1到达时,估计目标状态xk+1的条件MSE的下界满足式(3)[10]：

文献[15,18]中提供了一个更加直接的CPCRLB近似迭代公式，如式(4)所示：

根据目标运动的状态方程，量测方程以及式(4)，可以近似的计算出其FIM，如式(5)所示。

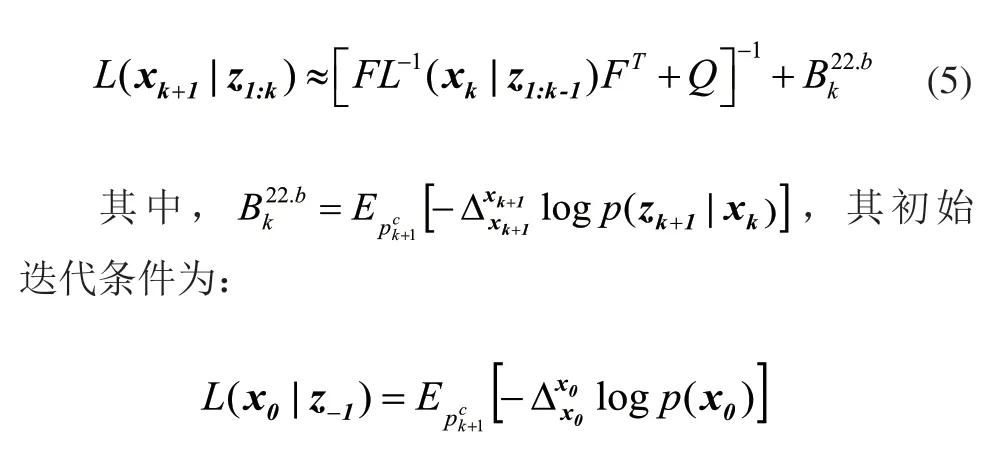
CPCRLB基于迄今为止获得的真实量测给出了目标跟踪过程中的一个预测性能边界。由于在目标跟踪过程中，只需要关心目标当前位置，因此采用FIM中对应于目标位置分量的和作为节点选择的适应度函数。假设在k+1时刻，从Na个传感器节点中选择Ns个传感器节点集为S×（k+1），则：

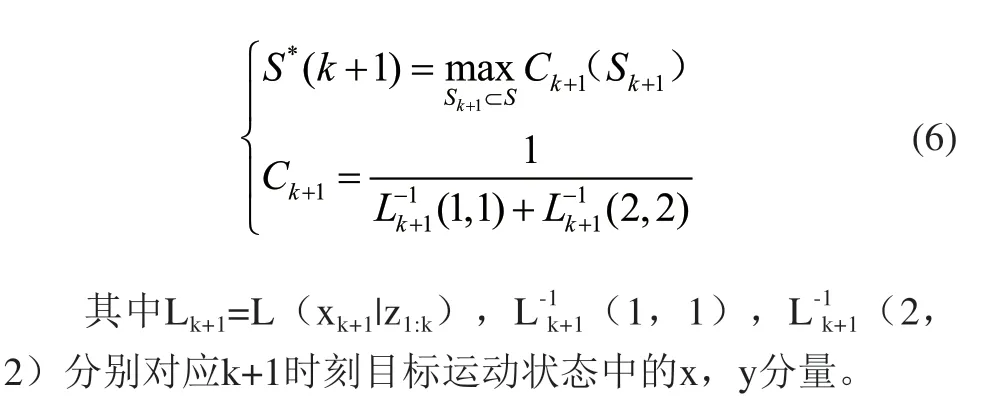
由式(6)可知，节点选择问题是一个具有约束条件的NP难组合优化问题[11]。这种问题目前广泛采用群优化算法进行求解。

3 基于自适应灰狼优化算法的CPCRLB的求解

3.1 灰狼优化算法

灰狼算法[14]主要是模拟灰狼种群的严格的金字塔等级制度，将最优解视为α狼（仅存在一个），次优解和第三优的解视为β狼和δ狼。其余的候选解被假定为ω狼。在GWO算法中狩猎（优化）过程由α狼，β狼，和δ狼引导，ω狼跟随上述狼群进行搜索。

1）包围猎物

在这个阶段，狼群所执行的最重要的活动是环绕猎物，如式(7)所示：

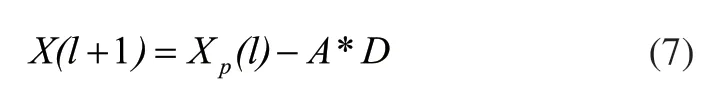
其中，当前迭代次数为l，D由式(8)求解，猎物的位置向量XP，X（l）表示在迭代次数为l时灰狼的位置矢量。

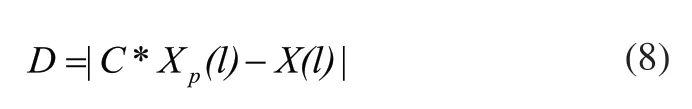
A和C表示向量系数，可由式(9)求解。

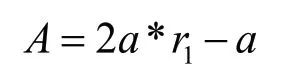
其中，α为收敛因子，r1和r2分别为[0，1]之间的随机数。

2）狩猎阶段

灰狼能够识别猎物的位置并包围它们。狩猎通常由α狼引导，β狼和δ狼也可能偶尔参与狩猎。通过α狼，β狼和δ狼估计猎物的位置，ω狼随机更新它们的位置，如式(10)～式(12)所示。

3.2 自适应二进制灰狼优化算法

由式(10)可知，等级较低的狼根据依靠α狼更新自身位置，所以当等级高的狼陷入局部最优时，等级低的狼很可能会跟随他们陷入局部最优。针对以上问题，采用以下方法进行改进。

3.2.1 非线性自适应收敛因子

在群智能优化方法中，寻找全局最优通常分为两个基本阶段:探索阶段和开发阶段。在探索阶段，算法尝试着搜索整个解空间，而不是围绕局部进行搜索。在开发阶段，算法使用前阶段获取的信息来收敛于全局最优。探索阶段较长会大大增加算法的随机性，可能会产生不好的优化结果，而太长时间处于开发阶段又会降低算法的随机性，所以探索和开发两个阶段应该保持平衡。在GWO中，通过微调A和a可以平衡这两个阶段，以更快的收敛速度寻找全局最优。当|A|≥1时，算法处于探索阶段，灰狼倾向于偏离猎物,从而实现全局搜索，当|A|＜1时，算法处于开发阶段，灰狼趋向于猎物，从而实现局部搜索[12]。由式(9)可知，A的值或随着收敛因子a的值逐渐减小，文献[13]中a随着迭代次数的增加线性减少，在包围猎物时容易出现停滞，影响算法的搜索能力，很难满足现实中优化问题的多样性。

针对以上问题，提出了非线性自适应动态收敛因子，通过控制A的值来提高算法的全局和局部搜索能力。

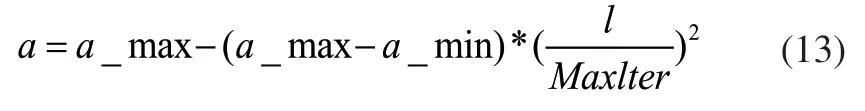
提出的自适应收敛因子表达式如式(13)所示：在式(24)中，a_max为收敛因子设置的最大值，a_min为收敛因子的最小值，Maxlter为总迭代次数。

3.2.2 V型函数位置更新原则

在进行目标跟踪时，通常需要将位置信息转换到二进制空间，转换函数是设计二进制优化算法时经常使用的方法，本文采用V型转换函数作为新的位置更新原则。这种位置更新原则的优点是其根据当前猎物位置来改变灰狼个体位置。当距离猎物位置较近时，V型函数鼓励灰狼停留在当前位置，以寻找最佳猎物位置，当距离猎物位置较远时，V型函数将灰狼位置转换为其当前位置的补码，即增加远离猎物位置的灰狼寻找新猎物位置的概率。

采用的V型函数如式(14)所示：

3.2.3 基于自适应二进制灰狼算法的CPCRLB的求解

1）约束条件A

观测区域内存在个目标和传感器节点，需要在不同的时刻选择最优节点分配给不同的目标。采用二进制编码的灰狼种群来表示传感器节点。种群POP为一个pop_n×Na（pop_n为种群个体数量）的矩阵设置如下：

如果选择的节点数的和（Ns’）大于需要的节点数的和（Ns），那么就从Ns’中随机选择Ns个节点数。如果选择的节点数的和（Ns’）小于需要的节点数的和（Ns），那就从剩余的节点数中以相同的概率选择（Ns- Ns’）个节点。

在开始迭代时，我们随机初始化种群，但是在算法的迭代过程中，对种群进行更新以后，产生的新的种群中被选择的传感器节点数可能不能满足需要的传感器节点数，因此在每次迭代后通过以下方法来满足被选择的传感器节点数等于需要的传感器节点数。

2）约束条件B

3）算法流程

综合上方提到的改进方法，自适应二进制灰狼算法（VBGWO）的流程（流程图如图2所示）如下：

STEP 1：设置种群POP，需要选择的节点数Ns，粒子群数目Np，最大迭代次数，初始的适应度函数值等参数。

STEP 2：根据约束条件A随机初始化灰狼种群。

STEP 3：根据式(6)计算适应度函数值，选取适应度值在前三的狼，并记录对应的位置。

STEP 4：利用式(13)计算收敛因子a的值，利用式(9)计算A，C的值。并利用式(10)～式(12)计算距离信息。

STEP 5：利用新的位置更新原则式(14)，产生新的种群。

STEP 6：判断产生的种群中被激活的节点个数是否满足约束条件B。

STEP 7：判断是否满足结束条件，若达到最大迭代次数，则输出最优位置及对应的适应度函数值，否则重复执行STEP（3～6）。

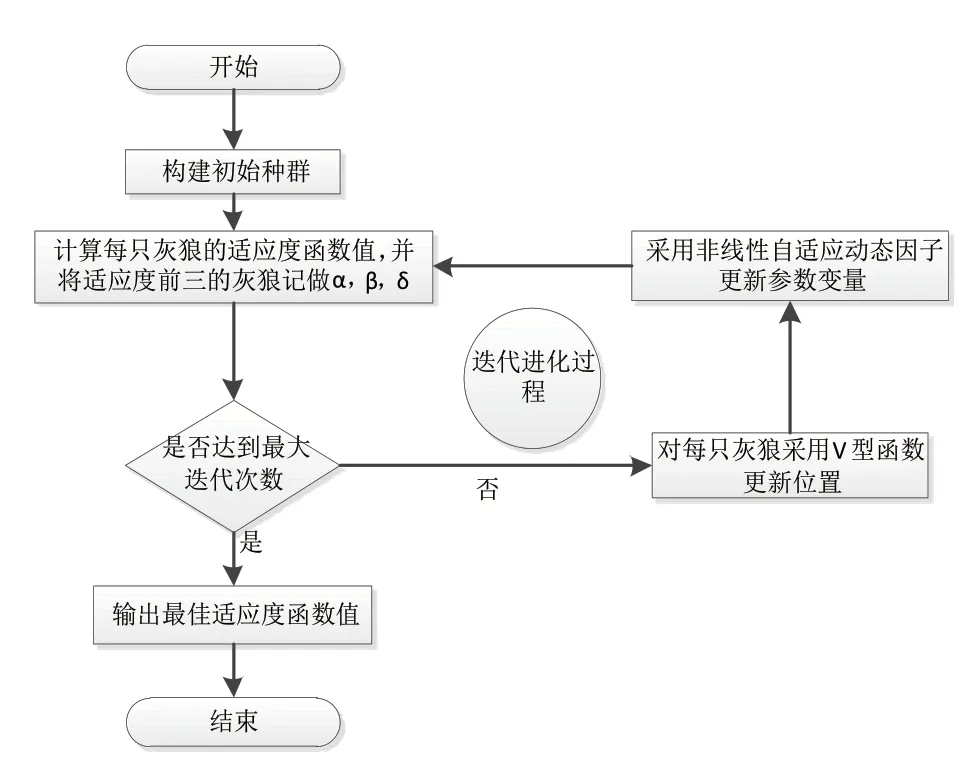
图1 自适应二进制算法流程图

4 实验仿真

分别为k时刻目标状态的估计值，Mc为蒙特卡罗次数，采用50次蒙特卡洛仿真。

表1给出了选取不同算法在k=15时的适应度函数值对比，由表可知，VBGWO能够获得更好的平均适应度函数值和最佳适应度函数，为了更好的对比各种算法的优劣性，我们随机选取其中一组优化过程如图2所示。

表1 50次蒙特卡洛 k=15时的适应度函数值对比

图2 Ns=50，Na=3时间k=15时适应度函数值

由图2可知，VBGWO大约在第12次时达到最佳函数值，而BPSO则大约在50次时达到最佳适应度函数值，说明VBGWO可以保持较高的收敛速度，同时，VBGWO在循环至10次左右时就获得了BPSO最终的适应度函数值，最终VBGWO取得的最佳函数值大于BPSO取得的适应度函数值，说明VBGWO拥有较高的收敛精度。在迭代后期，相对于其他两种算法，VBGWO的曲线并没有出现太多的阶跃，说明VBGWO能够更好的跳出局部最优并搜索到最佳适应度值。相对于上述两种算法，VBGWO采用了非线性自适应收敛因子和V型位置更新原则更好的提高了算法收敛速度和局部寻优能力，较快的收敛速度对于无线传感器网络的实时性是非常重要的，所以，VBGWO更加适合于无线传感器网络。

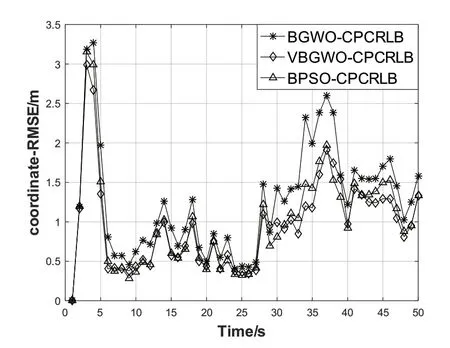
图3 不同算法的RMSE误差对比

图3采用不同算法从50个传感器节点中选取3个传感器节点的RMSE误差对比图，由图可知，VBGWO相对于其他两种算法，能选择一组最优的传感器观测节点集合,而且估计出的状态具有较小的均方根误差，所以拥有较佳的跟踪性能。

图4为k=15时从50，80，100个传感器节点中选取图6为k=15时从50，80，100个传感器节点中选取三个传感器节点的迭代过程。由图可知，随着传感器节点总数的增加，相对于其他两种算法，VBGWO依旧可以保持良好的收敛速度，说明VBGWO有较强的全局搜索能力。同时其最佳适应度函数值始终大于其他两种算法，表明其具有具有较小的跟踪误差。

图4 k=15时，当Ns=50，80，100（从上到下）时，选取3个传感器节点的适应度函数值

5 结语

主要研究了大规模传感器网络中的节点选择问题，采用基于粒子滤波的CPCRLB作为优化条件建立节点选择模型，并提出自适应二进制灰狼优化算法进行模型求解。仿真结果表明，采用自适应动态收敛因子和V型函数的自适应二进制灰狼算法针对于节点选择问题是有效的，其拥有较高的收敛速度，能够避免陷入局部最优。后续的研究工作是主要是将目前提出的算法应用于无线传感器网络多传感器多目标跟踪时的节点选择问题。