晶圆传输机器人末端执行器的拓扑优化

茹德志，于大泳

（200093 上海市 上海理工大学 机械工程学院）

0 引言

芯片来源于晶圆，将经过处理的晶圆通过晶圆传输系统传送到下一个工位进行下一步操作，以此往复，整个晶圆传输系统需要多方面的协调工作，而晶圆传输机器人在其中起到了关键性作用，它直接决定了晶圆传输的准确性以及生产效率，所以,晶圆传输机器人的研究对制造业的未来有着极其重要的意义。

晶圆传输机器人的主要功能是在不同工位之间按工序平稳、快速、高效地搬运晶圆，为了防止晶圆在搬运过程中使末端执行器发生变形而影响后面工作的持续进行，故应该对末端执行器的结构进行优化设计。本文研究的是串联的刚性杆柔性关节的平面关节机器人，其大臂由伺服电机驱动，小臂与末端执行器之间通过同步带来传输，通过固定的比例实现晶圆在水平面内沿径向的直线运动。在传输过程中，多次传输晶圆会导致末端执行器不可避免地发生振动和产生形变，从而导致晶圆的滑落与偏移，所以，必须对末端执行器的振动和形变进行抑制[1]。

随着全球半导体产业的迅猛发展，对晶圆规格提出了更高的要求，并呈现出了两种发展趋势：一是不断降低芯片的特征尺寸；二是不断扩大晶圆的直径，也就是从特征尺寸为 200 mm，0.35 um进入到了 300 mm，0.13 um 时代，450 mm，0.035 um的晶圆也逐渐投入生产[2]。这意味着晶圆变得更加脆弱易碎，对晶圆传输机器人的设计要求会更严谨，其中，对末端执行器的优化设计则是首个要被考虑的方面。对于形变问题，要采用静力学仿真分析，获得形变和应力的变化趋势；对于振动问题，要采用动力学模态分析来确定结构的振动特性，获得固有频率和振型。为了避免发生共振，更好地传输晶圆，末端执行器的固有频率要符合相应的要求。

目前，晶圆传输机器人从结构类型上主要有2 种基本类型：平面关节型（SCARA 型）晶圆传输机器人和极坐标型（R-θ型）晶圆传输机器人。其中，R-θ型晶圆传输机器人共有3 个自由度，R 向直线运动，θ向旋转运动，Z 向升降运动，其水平部分包括大臂、小臂和末端执行器，这种结构工作方式较为简单，不易发生故障，可以按照要求沿着径向做稳定直线运动[3]，如图1 所示。本文是对晶圆传输机器人末端执行器的结构进行优化分析[4]。

1 三维建模并做静力学分析

1.1 三维建模

使用三维UG 建模软件绘出末端执行器的简化模型。末端执行器的尺寸设计取决于所传输的晶圆尺寸，本文选取了最为常见的300 mm 晶圆进行研究，设计末端执行器的总体长度为400 mm，总体宽度为 220 mm，总体厚度为5 mm，其具体的结构形式如图2 所示。

1.2 划分网格

对末端执行器进行网格划分。对于三维几何体来说，网格划分基本有3 种方法：Automatic(自动网格划分)、Tetrahedrons(四面体网格划分)和Hex Dominant (六面体主导网格划分)，本文选择了Automatic 划分网格。末端执行器的材料选取超硬铝（LC4），各向同性，介质均匀，其杨氏弹性模量约为68 GPa，泊松比约为0.33，屈服强度约为680 MPa，标准密度为2.7×103 kg/m3。划分后的网格如图 3 所示。

1.3 静力学分析

利用ANSYS 中自带的Static Structural 模块对末端执行器的模型进行静力学分析，考虑模型所受到的约束力，先对连接小臂一端的部分进行固定，然后对4 个凸点施加由晶圆所产生的压力1.28 N，同时要考虑重力加速度产生的影响，仿真结果如图4 所示。

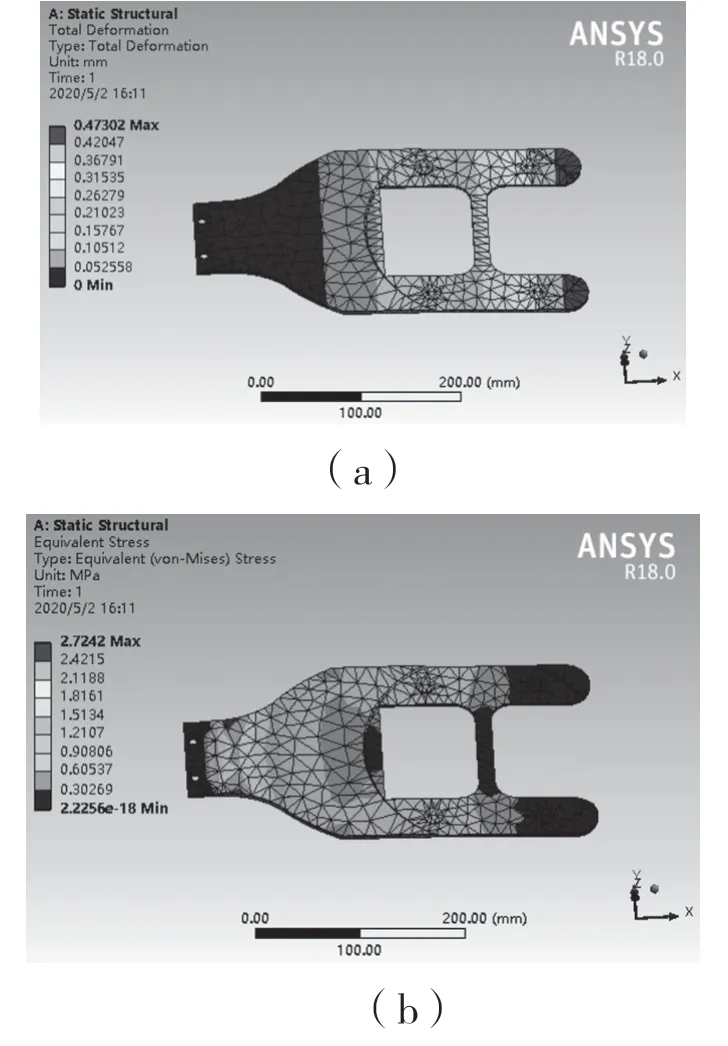
图4 末端执行器的变形仿真图Fig.4 Deformation simulation diagram of end-effector

通过图4 可以看出，末端执行器的最大应变发生在末端执行器两尾端，其最大总变形量为0.473 mm，对传输晶圆不会产生明显的影响；同时，末端执行器最大应力发生在其与小臂连接的一端，意味着在此位置最容易发生失效的问题，而其最大应力值2.724 MPa，远小于超硬铝的屈服强度 680 MPa，所以该末端执行器的强度符合设计要求。

2 末端执行器结构的拓扑优化

2.1 拓扑优化的理论基础

拓扑优化是指形状优化，有时也称为外形优化。其目标是寻找承受单载荷或者多载荷的物体的最佳材料分布方案。拓扑优化不需要依赖原有构型和工程师的经验，其不同于传统优化方式，既不需要定义结构参数，也不需要相应的优化变量，所以目前得到众多研究者的青睐[5-6]。优化过程中的目标函数、设计变量以及状态变量都是事先被预定义好的，所以用户只需要给出结构的相应参数（如材料属性、所受载荷等）和期望要减少的材料的比例。在符合给定的相应结构约束的前提下，拓扑优化通过减少结构的变形量，可以做到提高优化结构的刚度和降低运动惯量的目的。

优化设计方法是一种规格化的设计方法，它首先要求将设计问题按优化设计所规定的格式建立数学模型，选择合适的优化方法及计算机程序，然后再在符合结构设计要求的前提下进行相应的迭代运算，直至取得目标函数的极值，进而找到最优的设计方案[7]。

优化设计过程的数学模型可表示为

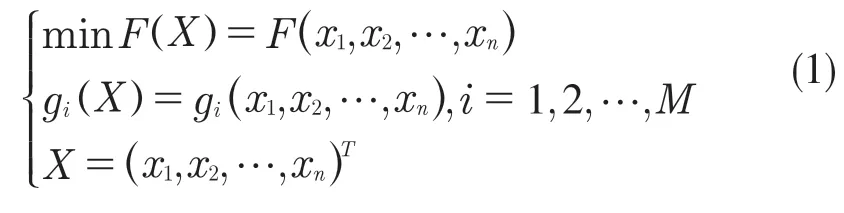
式中：F（X）——设计变量的目标函数；gi（X）——状态变量；X——设计变量。

设计变量也就是目标函数中的自变量，最终的最优结果是通过不断调整设计变量来实现的，每一个需要优化的变量都会有它的上下极限值，所有优化过程中必须规定X 所有元素xn（n=1,2,…,N）的上限值、下限值，它指定了设计变量的变化范围；状态变量对应于对优化过程的约束条件，即约束设计的数值，也是与设计变量有关的函数；目标函数则是设计变量函数的最大或者最小值（即最优解）。

通常基于ANSYS Workbench拓扑优化步骤为：

（1）将在三维UG 软件中绘制的模型导出符合ANSYS 的格式；

（2）打开ANSYS Workbench 主界面，把拓扑优化模块拉到Workbench 中；

（3）导入准备好的模型并划分网格；

（4）对模型施加固定约束、重力加速度以及模型所受载荷；

（5）在拓扑优化选项中，设置要去除的材料为你所想要的百分比；

（6）求解，即可得到想要的结果。

2.2 末端执行器的拓扑优化

本文利用ANSYS Workbench 中自带的Topology Optimization 模块对末端执行器的结构进行优化分析。Topology Optimization 模块能够在保证末端执行器的总体结构基本不变的前提下，尽可能地使其质量最小化，寻找对整体的结构强度不具有负面作用的可去除面积。

为了保证末端执行器结构的整体形状，先选择优化去除掉50%的材料，最终实现去除材料25%的目标。对末端执行器进行拓扑优化，优化结果如图5 所示。图中淡灰色部分为保留部分，深灰色部分为可去除部分[8]。

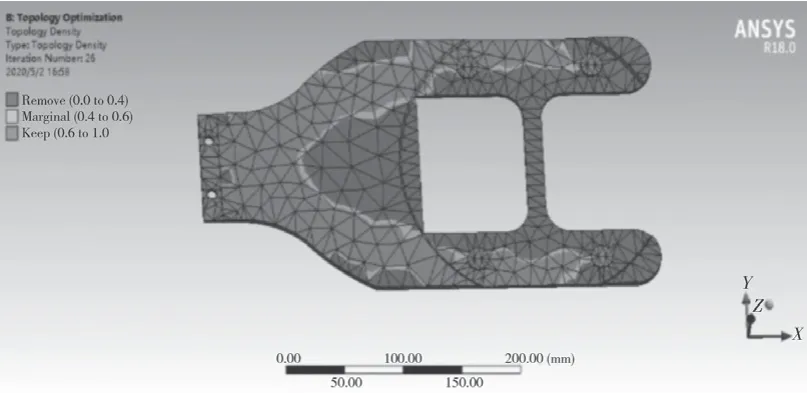
图5 拓扑优化结果Fig.5 Topology optimization results

通过分析拓扑优化后的结果，结合实际情况对末端执行器模型进行修改，仿照VCD 碟盘的设计，本文选择对模型两侧进行去除，呈现出2个弧形孔，以及对靠近小臂一段的部分进行去除，修改后的模型如图6 所示。

图6 末端执行器优化结构Fig.6 Optimization of end-effector structure

3 优化结构的静力学分析

结构静力学分析是用于计算由那些不包括惯性和阻尼相应的载荷作用于结构或部件上引起的位移、应力、应变和力，结构静力学的特点是不考虑惯性和阻尼的影响。

首先,利用三维UG 建模软件UG 建立晶圆传输末端执行器的实体模型，然后借助 UG 与ANSYS Workbench 之间的接口技术，将其导入到ANSYS Workbench 中进行分析。

使用ANSYS Workbench 中自带的Topology Optimization 模块对新的末端执行器模型进行与1.3 相同的静力学分析，处理结果如图7 所示。

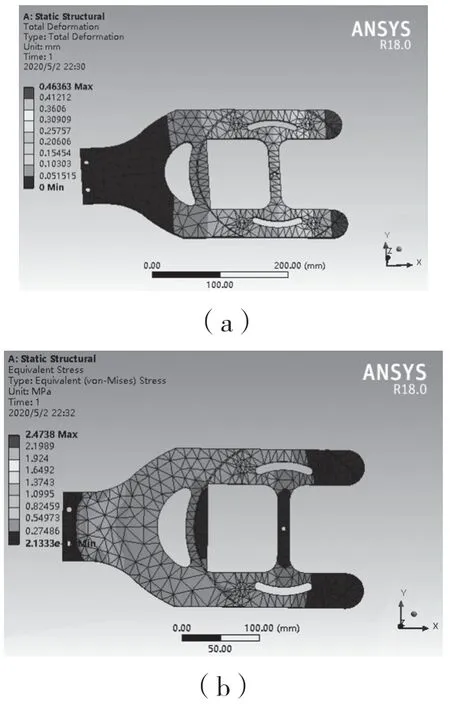
图7 优化结构的变形仿真图Fig.7 Deformation simulation diagram of optimized structure

依据ANSYS 中对末端执行器模型进行的静力学分析，将拓扑优化后的结构变形仿真图与初步设计结构的变形仿真图进行对比分析，对比数据见表1。

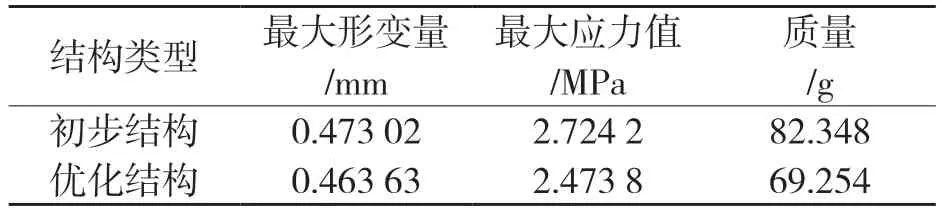
表1 末端执行器优化前后变形量对比Tab.1 Comparison of deformation before and after endeffector optimization

对比表1 中的数据可以看出，末端执行器的最大变形量由原来的0.473 02 mm 减小到 0.463 63 mm（减少了0.009 39 mm），最大应力值由原来的2.724 2 MPa 减小到了优化后的 2.473 8 MPa（减少了0.250 4 MPa），质量由原来的82.348 g 变为优化后的69.254 g（减少了13.094 g），说明拓扑优化后的新结构，既减少了初步设计结构的质量，也改善了其强度，同时结构更加美观。

4 优化结构的动力学分析

晶圆传输机器人在传输晶圆的的过程中会发生振动，同时,会和机械手臂发生共振现象，所以需要对拓扑优化后的模型进行动力学分析，确保其传输的稳定性[9-12]。

动力学分析方法主要有模态分析和谐响应分析两种，本文采取模态分析的方法。使用模态分析可以确定设计中的结构或机器部件的振动特性（固有频率和振型），它也可以确定一个结构的固有频率和振型。固有频率和振型是承受动态荷载结构设计中的重要参数。如果要进行谱分析或模态叠加法谐响应分析或瞬态动力学分析，固有频率和振型也是必要的。

ANSYS 的模态分析是一线性分析，任何非线性特性（如塑性和接触单元）即使定义了也将忽略，可进行有预应力模态分析、大变形静力分析后有预应力模态分析、循环对称结构的模态分析、有预应力的循环对称结构的模态分析、无阻尼和有阻尼结构的模态分析。

本文通过分析比较末端执行器各阶的固有频率及振型与机械手臂的振动频率之间的关系，从而验证模型的合理性。

利用ANSYS Workbench 软件中自带的Modal模块，对经拓扑优化后的末端执行器结构进行模态分析。本文只对模型的前6 阶进行模态分析，如图8 为各阶固有模态振型及固有频率。

对拓扑优化后的末端执行器结构进行模态分析，得到末端执行器前6 阶固有频率及振型情况，如表2 所示。

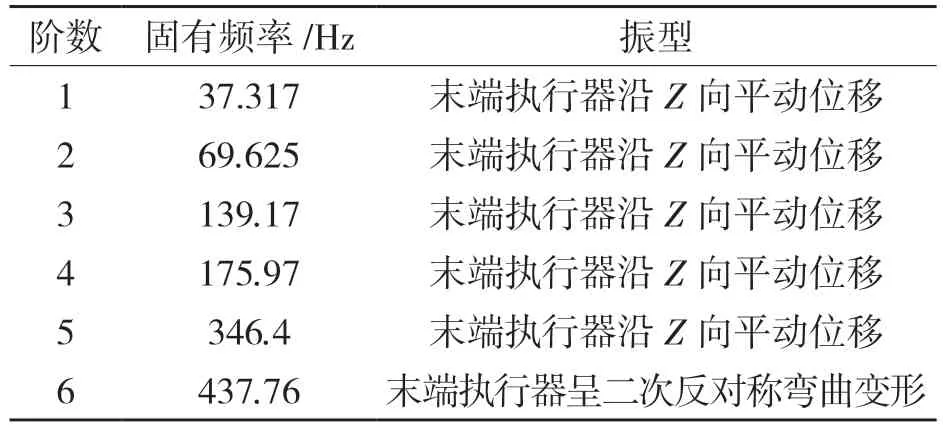
表2 末端执行器的模态参数及振型描述Tab.2 Description of modal parameters and modes of end-effector

通过查阅相关资料得知，现有机器人手臂的振动频率约为23 Hz，而本文设计的末端执行器一阶固有频率为 37.317 Hz，大于晶圆传输机械手手臂的振动频率，所以可以判定优化后的末端执行器不会和机械手臂发生共振现象，满足动态特性的要求。

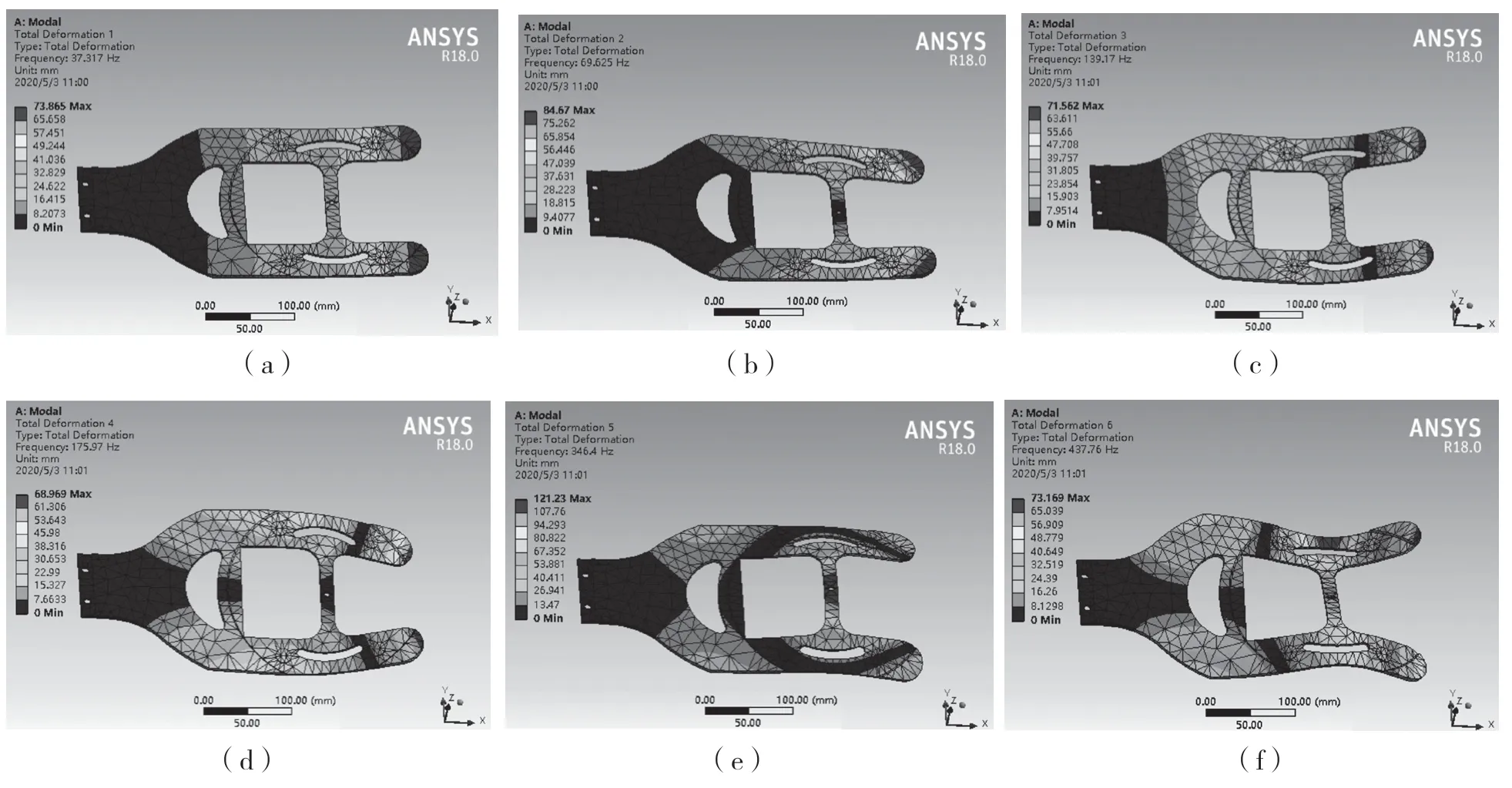
图8 末端执行器的模态振型Fig.8 Modal shape of end-effector

5 结语

本文对晶圆传输机器人的末端执行器进行初步设计和拓扑优化设计，并对优化后的结构进行静力学和动力学模态分析，验证了新的机械结构的合理性，新结构减少了质量，节省了材料和成本，同时在不影响末端执行器的强度条件下，满足晶圆高效、精确、稳定的传输。