钢筋混凝土圆形截面非均匀配筋的图算法

罗 莎， 周东华

(昆明理工大学 建筑工程学院，昆明 650224)

1 引 言

目前圆形截面的配筋计算有两大特点，一是计算困难，二是已有的配筋计算公式仅针对钢筋均匀布置的情况。计算困难是因为存在双重非线性(材料和截面宽度变化的非线性)，对此《混凝土结构设计规范》[1](以下简称为规范)给出了计算圆形截面均匀配筋的超越方程组，但须联立迭代求解，难以手算。另外，规范公式是针对均匀配筋推导的，均匀配筋有不合理的一面，即靠近中性轴区域的钢筋应力很小，钢筋强度得不到发挥，这种布筋方式是不经济的[2-6]，较好的布筋方式应该是受力钢筋布置在远离中性轴的外围区域，而靠近中性轴的区域仅布置构造钢筋。当构件尺寸(直径和长度)很大时(如抗滑桩和深桩基等)，这种布筋方式的经济性和合理性尤为突出。本文针对以上两个特点展开，一要解决能手算的问题，二要解决非均匀配筋的计算问题，即提供一个通用的计算方法。

为了避免求解规范中求解圆形截面计算配筋的超越方程组[7-12],本文从应变出发，由应变计算应力，再由应力计算内力[13-16]。从应变出发指的是要已知应变，为此要确定所有可能的应变及应变范围，要做到这一点，只须按照规范中给出的混凝土和钢筋的本构关系就能确定，即主要根据屈服应变和极限应变来确定，另还将根据这些关键的应变点来对可能的应变进行分区，以便公式推导和计算。

2 计算方法和公式推导

2.1 本构关系

采用规范6.2.1给出的混凝土和钢筋本构关系，如图1所示。

图1 本构关系

混凝土及钢筋的本构关系的数学表达式为

(1)

(2)

式中εc和εs分别为混凝土和钢筋应变，σc和σs分别为混凝土和钢筋应力，fc为混凝土的抗压强度，fy为钢筋的屈服强度。

2.2 混凝土及钢筋的应变区域划分

本文方法最关键的一步是由应变通过本构关系确定应力，根据规范6.2.1规定，可构建出 图2 的3个应变区域。这3个区域能反映大偏拉、纯弯、大偏压和小偏压下的应变状态。3个应变区域共有的特点是，在每个区域内总有一应变为极限应变，或是截面上边缘的混凝土应变，或截面下部钢筋的应变达到极限应变，未达到极限应变的另一侧的应变则可变化，即可取不同的值，这样在所有应变组合都含有一个极限应变，即为承载力极限状态，其破坏形式可为受拉边先破坏，或受压边先破坏，或受拉边和受压边同时破坏。

图2 混凝土和钢筋的应变变化区域

有了应变分区及外边界，就可选取不同的应变组合(一个固定应变分别与不同可变应变的组合)加上考虑混凝土和钢筋的本构关系来确定应力的大小，然后将应力在截面上积分，从而得到截面内力。

图2的3个应变区域分别对应图3的4种受力状态，其分别是，大偏拉、纯弯、大偏压和小偏压应变状态下的应力分布图。

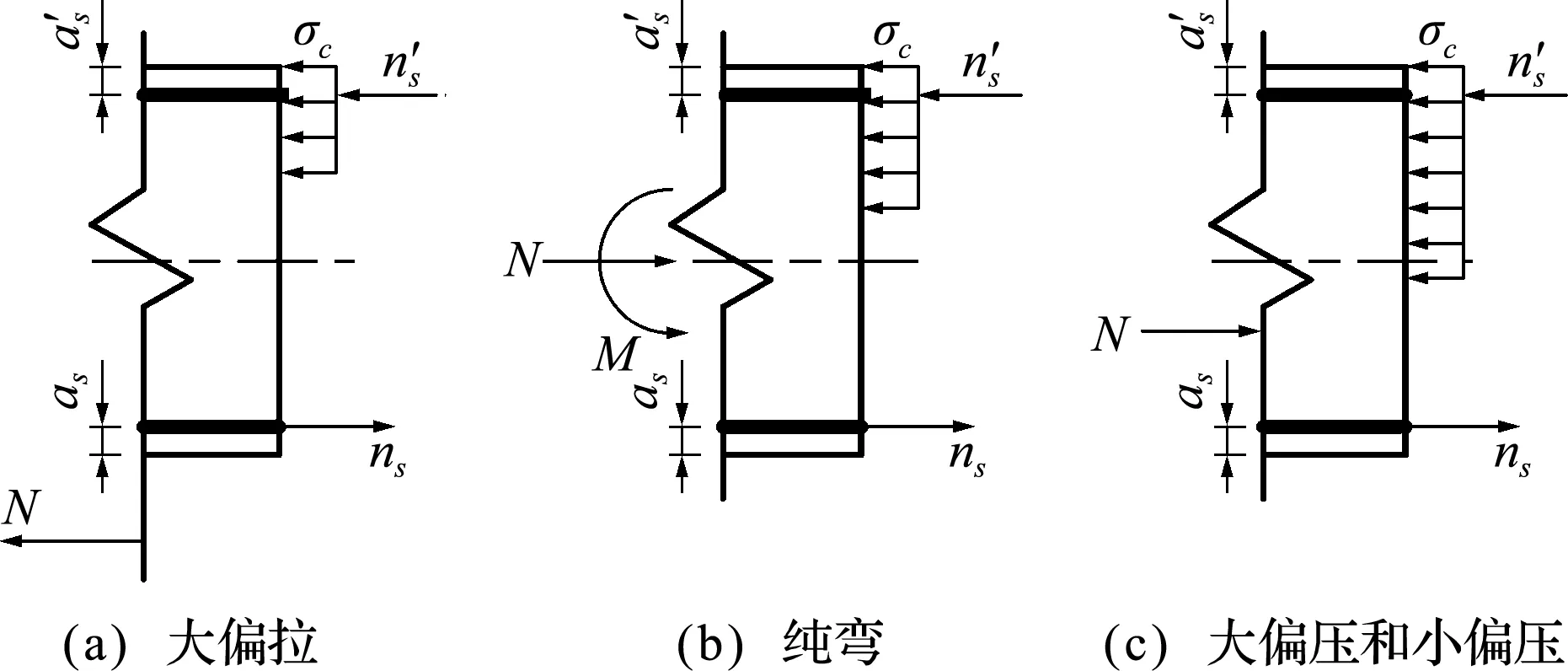
图3 应力分布

下面对图2的应变分区的特点加以说明。

区域①： 下部钢筋应变为固定，其值为极限应变(εs=10‰)，上边缘混凝土应变可变化，其值为εc 1=0‰～-3.3‰，中性轴由截面上边缘逐渐下移进入截面，受力状态可为大偏心受拉和纯弯。

区域②： 截面上边缘混凝土应变为固定，其值为极限应变(εc 1=-3.3‰)，下部受拉钢筋应变则可变化，其变化范围为εs=10‰～εy。截面受力状态为纯弯或大偏心受压。

区域③： 混凝土上边缘应变仍为固定，即εc 1=-3.3‰，下部受拉钢筋的应变可变化，其变化范围为εs=εy～0‰，由于受拉钢筋不屈服，所以截面受力状态为小偏心受压。

有了上述所划分的3个应变区域，不仅可知应变的变化范围，还让可变化的应变成为已知量，即将可变化的应变分别赋以不同的值，便可由本构关系得到相应的应力值。与规范公式相比，划分应变区域的方式更加完善，不需要求解超越方程，减小计算难度。

2.3 公式推导过程

2.3.1 混凝土截面应力和内力的计算

利用图4应变的几何关系可计算出受压区高度x,由x可确定截面高度范围内任意纤维处的应变εc i，

(3，4)

(5)

(6)

将式(6)代入式(1)的混凝土本构关系可得任意纤维处应力的计算表达式，

(7)

图4 截面参数及应变

由此可对微面积上的应力和应力矩积分，来计算轴力和弯矩。计算时，弯矩的取矩点选为下部钢筋的合力点。

当εc 1=-2.0‰～-3.3‰时为矩形区段，此区段内轴力为面积的计算，弯矩为面积距的计算，由此可得

(8a)

(8b)

当εc 1=0‰～-2.0‰时为抛物线区段，积分后可得

(9a)

(9b)

上述计算轴力和弯矩的公式是按照混凝土本构关系来确定，但此时的轴力和弯矩与混凝土强度和截面尺寸是相关的，所以将式(8a,9a)除以πr2fc和将式(8b,9b)除以πr3fc，就可得到式(10a,10b)的无量纲轴力和弯矩,

(10a)

图5 应变εc 1≤-2.0‰时的应力分布

(10b)

式(10a，10b)的积分上限为圆顶，下限为中性轴高度处所对应的圆心角，由式(11)计算得

(11)

当应变范围为0‰>εc 1>-2.0‰(区域①)，所对应的hi值为0，x，如图6所示。

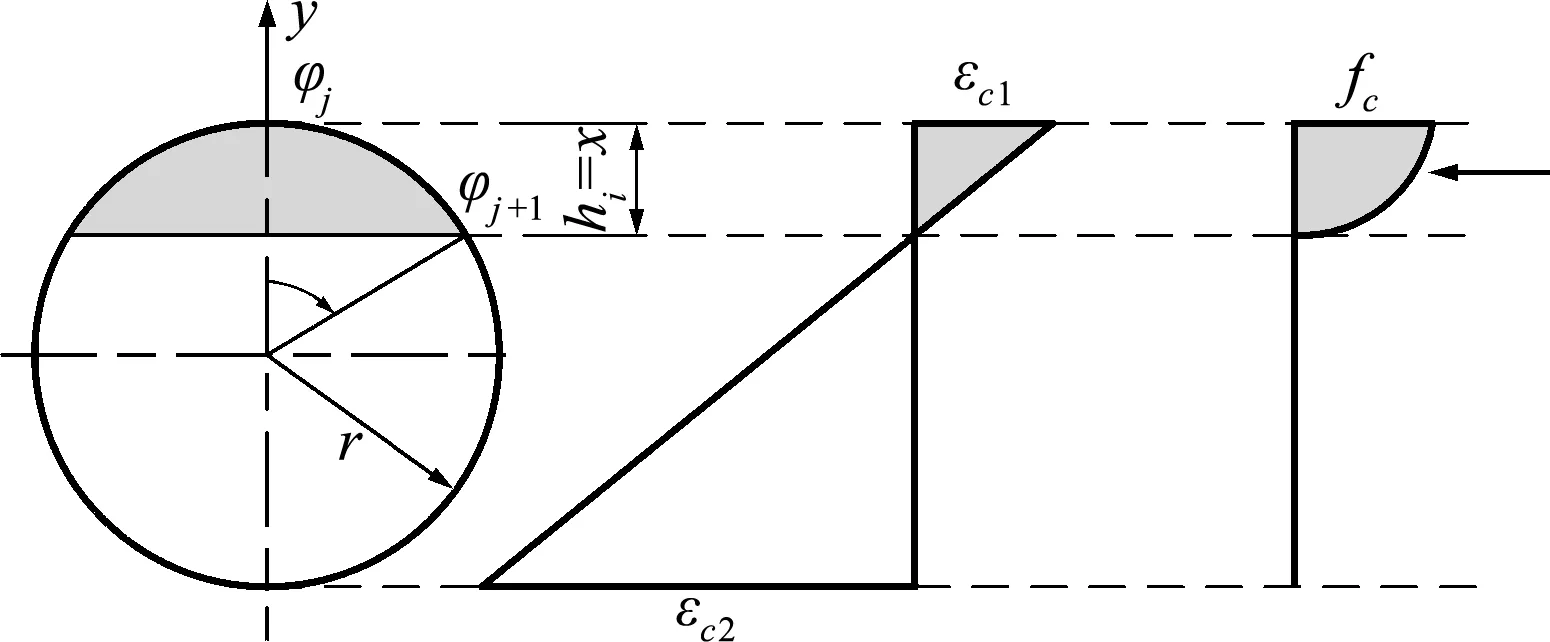
图6 积分上下限对应的圆心角

可知在不同的应变区域，应力分布形状是变化的，当应变范围为-2.0‰>εc 1>-3.3‰时(区域①②③)，所对应的hi值为0，x-a，x。

2.3.2 受压区高度系数kx及内力臂系数kz

对于0‰≥εc 1>-2.0‰以及εc 1≤-2.0‰范围，截面内力及内力臂如图7所示。

图7 截面内力及内力臂

由几何关系易知，

(12)

令x=kxh0，当应变区域处于区域①时，取εs=10‰，则有

(13)

同理可得内力臂系数kz，

(14)

式中a=m/n。

2.3.3 钢筋面积的求解

截面上的弯矩和轴力如图8所示，则钢筋面积的求解存在以下情况，计算方法为

(1) 单筋

当截面上没有轴力时，受拉钢筋面积为

(15)

式中z=kzh0。

当截面上存在轴力时，应将轴力移至钢筋合力处，如式(16)，轴力的符号规定为拉力为正，压力为负。

Ms=M-N(D/2-as)

(16)

(17)

当受拉钢筋应变达到或超过屈服应变时(区域①和区域②)，σs=fy，当小于屈服应变时(区域③)，σs=Esεs。

(2) 双筋

当截面上设置受压钢筋时，为充分利用混凝土强度，让超出极限弯矩部分ΔM由受压钢筋来承担，

ΔM=M-M*

(18)

图8 截面上的弯矩和轴力

级别有关，当使用HRB400级钢筋时，m*=0.379。

受压钢筋为

(19)

受拉钢筋为

(20)

当存在轴力时，需先求得Ms，可得受拉钢筋为

(21)

由此，通过3个应变区域的划分可确定每一种受力情况下的应变变化范围，由应变大小通过混凝土和钢筋的本构关系确定应力大小，再由积分可知轴力和弯矩。

需要补充说明的是，前面推导所得公式是针对受力筋，受力筋以外的区域按照构造配置钢筋。

3 算例分析

算例1D=1000 mm，M=1000 kN·m，钢筋等级选用HRB400，混凝土强度等级选用C30。按本文介绍方法计算配筋。

(1) 按规范

规范公式只针对全截面均匀配筋，将已知量代入公式，可得

图9 无量纲弯矩与截面计算系数关系诺模图

求解方程，得As=6870 mm2。

(2) 按本文计算方法

由m查图9得kz=0.94。

3307 mm2

本文方法与规范所得的钢筋面积之比为3307/6870=0.48，可节省钢筋52%。

算例2D=1000 mm，M=900 kN·m，N=-800 kN,钢筋等级选用HRB400，混凝土强度等级选用C30。按本文介绍方法计算配筋。

(1) 按规范

规范公式只针对全截面均匀配筋，将已知量代入公式，可得

求解方程，得As=8352 mm2。

(2) 按本文计算方法

由m查图9得kz=0.94。

本文方法与规范所得的钢筋面积之比为1796/8352=0.22，可节省钢筋78%。

算例3D=1000 mm，M=2500 kN·m，N=-2200 kN,钢筋等级选用HRB400，混凝土强度等级选用C30。按本文介绍方法计算配筋。

(1) 按规范

规范公式只针对全截面均匀配筋，将已知量代入公式，可得

求解方程，得As=29653 mm2。

(2) 按本文计算方法

ΔM=Ms-m*πr3fc=3366-0.379×π×5003×

14.3=1238 kN·m

由m≥m*，需按照双筋进行配筋，查图9可得kz=0.87。

本文方法与规范所得的钢筋面积之比为 5862×2/29653=0.39，可节省钢筋61%。

4 结 论

(1) 本文可以使不同级别的混凝土和钢筋都使用一个无量纲图表，与规范相比，无量纲图表法可以计算3个应变区域，不用求解超越方程，相关计算变得简单和快捷。

(2) 规范只有圆形均匀配筋的计算公式，所以在非均匀配筋的情况下无法计算配筋，本文提供了非均匀配筋的计算方法，且考虑了非均匀配筋时因分布角度而改变的钢筋重心位置，使计算结果更加精确，采用非均匀配筋可以减少钢筋面积，节省钢筋用量，充分利用钢筋混凝土的强度，钢筋配置适宜，满足新规范要求，为工程设计人员提供了一定的参考价值。