基于持续同调的边坡破坏过程的拓扑特征研究
2021-04-30陈龙飞游世辉刘小飞赵小英
陈龙飞, 游世辉, 刘小飞, 赵小英
(1.湘潭大学 土木工程与力学学院,湘潭 411105; 2.枣庄学院 机电工程学院,枣庄 277160;3.莫斯科大学,莫斯科)
1 引 言
边坡失稳问题广泛存在于岩土工程、环境科学和交通运输等诸多领域。边坡受到雨水冲刷、地震以及撞击作用时会发生失稳造成滑坡,从而给社会和人民造成巨大的经济损失和生命威胁。因此,边坡失稳问题的研究具有非常重要的理论和科学意义。
边坡失稳问题的研究主要有实验和数值分析法等。数值分析法包含离散元法[1]和有限法等。数值分析法的优势在于低成本、可重复和可模拟复杂地质条件。目前,国内外学者利用离散元对岩体及边坡稳定性问题进行了大量的研究。Fakhimi 等[2-5]通过模拟单轴压缩试验对岩体的变形破坏特性、宏观性质和微观特征进行了研究。杨冰等[6-10]基于PFC2D和EDEM软件对边坡失稳过程的宏观响应进行了研究和探讨。苏永华等[11]利用双强度折减法对边坡的极限承载力进行了研究;潘敏等[12]提出了基于稀疏网格配点法的边坡可靠度分析方法,为进行复杂的边坡可靠度分析提供了一条有效的途径。
早期对于边坡破坏的研究都是通过实验的方式进行的,但这种方法只涉及一种尺度,而边坡破坏是一个动态的多尺度的破坏过程,涉及到从微孔洞的损伤积累到宏观的裂缝形成,微观和宏观之间相互影响,微观的力学演化是导致宏观力学演化的根源。宏细观系统存在跨尺度的关联性、层次性和随机性,所以需要找到一种能覆盖所有尺度的研究方法,而持续同调就是一种可以覆盖连续尺度的拓扑化描述方法。所以用持续同调方法可以分析边坡从裂缝生成到发生失稳破坏的整个过程,找到失稳临界状态对应的持续同调拓扑特征,从而为边坡破坏预测提供新的工具。
目前,离散单元法等非连续变形方法在国内获得了推广[13],在边坡稳定性定量评价方面尚不成熟,更没有将拓扑特征分析应用于边坡破坏过程表征的例子。所以本文引入持续同调理论,对边坡进行拓扑特征描述。这具有极为重要的工程和科学意义。工程方面,运用离散元方法和持续同调理论,可以对边坡处于外荷载作用下的破坏特征进行研究,从而可以更好地了解边坡的破坏机理,为工程防护提供理论依据。其科学意义在于,通过在边坡上应用持续同调理论,研究其拓扑特征,将持续同调拓扑特征与边坡失稳特征联系,推广了理论的应用范围,验证了理论的正确性及适用性。
近年来,持续同调在图像处理和目标识别等领域取得了很大的进展。张景亮等[14]运用持续同调和单纯复行同调群的计算方法对图像进行分类和识别。通过计算单纯复形的同调得到相应的条形码,基于该条形码来获取图像的拓扑特征以及相应的几何结构信息。
本文采用离散元软件UDEC,对边坡稳定性进行了研究,分析了其失稳破坏过程,并分析了不同时间段边坡的力学行为。最后对边坡进行拓扑分析,运用软件自带的强度折减法得出边坡整体的安全系数来判别稳定性,把边坡看成是由各岩块组成的多尺度结构网络,并借助持续同调理论分析边坡的拓扑特征,获得条码图,然后将持续同调理论和支持向量机的方法结合,对边坡条码图进行特征提取,保留了与其类别相关的主要特征,建立了边坡失稳与其拓扑特征的联系,并基于条码图参数来描述边坡的损伤演化规律。具体执行流程如下。
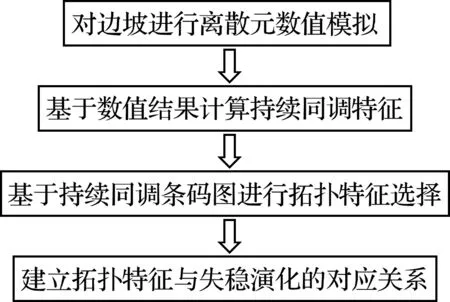
由于持续同调研究的是拓扑特征,不同的边坡在材料、所处状态及边界约束条件等方面可能不尽相同,但都会经历一个从裂缝生成、积累演化到致使边坡最终失稳破坏的过程。如果将整个边坡看成一个由岩块组成的网络,那么这个网络的演化规律是一致的,即其内在的拓扑特征是相同的。将本文结果与强度折减法等传统失稳判据相比,结果也具有一致性。所以该研究方法及结果具有广泛适用性。
2 持续同调理论
2.1 单纯复形
单纯复形是通过不同的单纯形连接起来而构成的,其边界即表面。RN空间中,单纯复形满足如下定义。
K包含K中单形的每一个面;
K中任何两个单形的交是其每个单形的面。
由定义可知,单纯复形中两个不同的单纯形,其交点必须是公共点。如本文可以用线段(一维单纯形)连接两个三角形(二维单纯形)来形成一个单纯复形。构成单纯复形的最高维单纯形的维数就是它的维度。显然图1的复形就是二维单纯复形,因为构成它的最高维单纯形为二维的三角形。
同时要注意区分特殊的单纯形和单纯复形。如同样是三角形,一个是三条边首尾相接,那么该单纯复形就是由1维单纯形构成的。而如果把这个三角形内部填满,即可以取到内部的每一个点,那就是2维单纯形,它是一个单纯形。这就凸显了涂色的重要性。
单纯形的表面是其边界,当描述单纯形或复形的时候,传统地在单纯形表面染色使其清楚地表明它是固体。如在画图时,本文将三个1维单纯形首尾相接后仍是1维单纯复形,尽管其看起来很像2维单纯形。如果在表面涂上色,那就可以确定它是一个得到填充的2维单纯形,如图3所示。
2.2 同调群
群是一种数学结构,用来描述所有具有对称概念的东西,如今已发展成为一个完整的数学体系群论。群是一个很普遍的概念,可以应用在很多对象上。如数学中的等边三角形具有对称轴,而且在旋转120°以后可以回到原来的结构,那么这种几何结构就可以用群来描述,群论为表述这类操作提供了很好的工具。群的准确定义为
一个集合G以及其上定义的一个二元运算就构成了群,该二元运算将a,b∈G映射到c∈G,写作a*b=c(∀a,b,c∈G)。当这个集合和定义的二元运算满足以下三个条件时,便是有效的群。
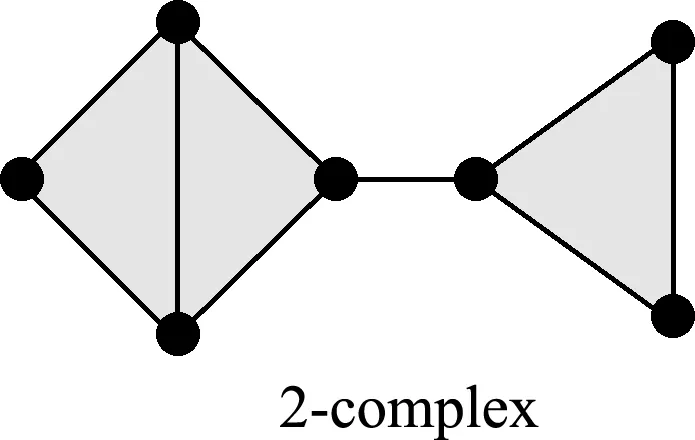
图1 2维单纯复形
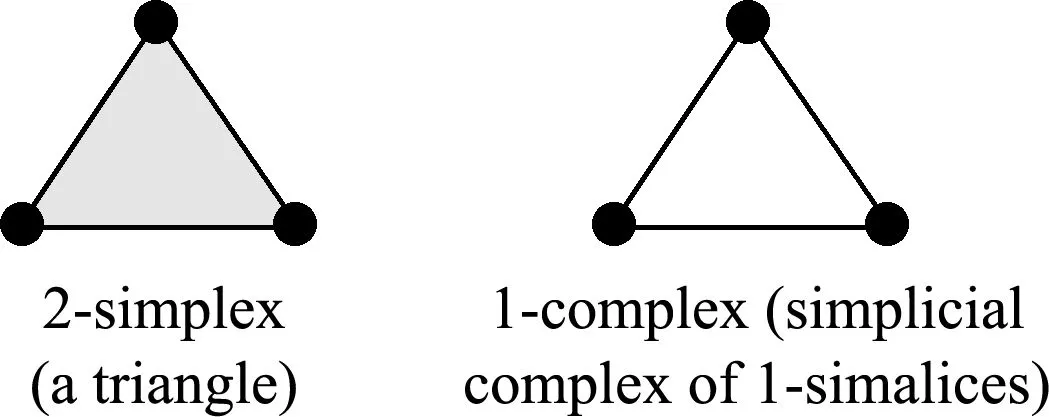
图2 涂色区别
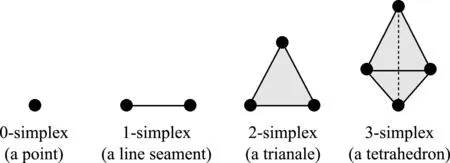
图3 各维单纯形
(1) 结合律
∀a,b,c∈G,(a*b)*c=a*(b*c)
(2) 单位元。存在一个元素e∈G,G的元素a与e进行二元运算以后,仍映射回集合G中该元素本身,即a*e=e*a=a成立。而且该元素是唯一的,那么本文把e称为单位元素。
(3) 逆元。若任意a∈G,存在一个元素b∈G,使得a*b=b*a=e成立,其中e为单位元素,则b为a的逆元。如整数集和加法运算就可以构成一个群。因为两个数相加交换律(a+b)+c=a+(b+c),而且整数集中存在单位元0,任何数和0相加都得到其本身。任何元素的相反数就是其逆元,因为相反数与原数相加的和为单位元0。
(4) 同调群。第k个同调群是商群Hk=Zk/Bk。第k个同调群的序列称为第k个贝蒂数,并且满足βk=rankHk=rankZk-rankBk。
直观地来看,b0表示连通件的个数,b1表示一维孔洞数,b2表示由面围成的三维孔洞,更高维的依次类推。如一个环面的贝蒂数应该是b0=1,b1=2,b2=1。分别表示一个连接组件,两个一维孔,一个三维孔。
2.3 持续同调
持续同调是在同调的基础上引入了持续性,是同调的推广。同调是一个静态概念,而持续同调是一个变化的动态的过程。同调计算是在单纯复形上进行的,而持续同调则是在过滤嵌套复形上进行计算的,是一个持续的变化过程。持续同调的计算与同调群是密切相关的。
3 数值仿真
3.1 计算模型
离散元模型的建立参照江坪河水电站厂房后岩质边坡的实际情况,该边坡因临空面倾角很大,风化卸荷裂隙发育,最低处高程约为 380 m,坡高 100 m~120 m,垂直河流方向发育。边坡主要为厚层灰岩和泥灰岩经风化和雨水侵蚀作用下形成的边坡。强风化岩体水平深度 5 m~10 m,断层与层面以小角度倾向坡内,组成不稳定楔体的可能性不大。在各类结构面中,顺坡向陡倾角卸荷裂隙发育,其深度为 1 m~10 m,是影响边坡稳定的控制性结构面。本文参照上述实际边坡,采用离散元软件UDEC对边坡失稳过程进行了数值模拟计算,离散元模型如图4所示,本文设置的整个岩质边坡高20 m,宽25 m,危岩高20 m,危岩设有竖直和水平两个方向的节理,间距2 m。岩块可以平移和转动,而节理则可以压缩和分离。所以该模型还允许产生岩块脱落等大变形。岩体和节理的物理力学参数列入表1和表2。
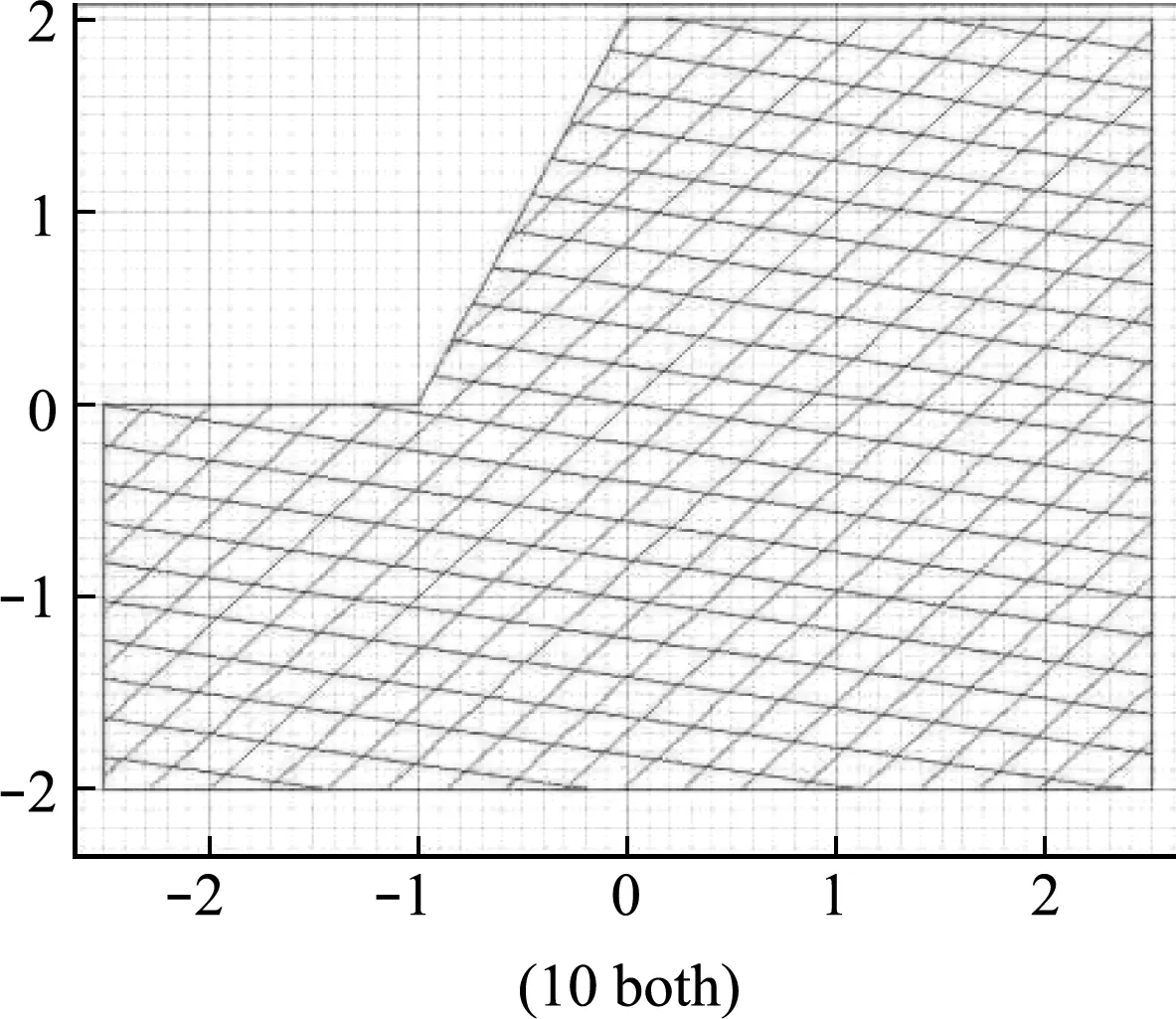
图4 岩质边坡模型
3.2 岩体动态响应分析
把危岩的右侧和底部设置为粘性接触,顶部和左侧为自由边界,不施加约束。然后在底部施加一个大小为10 MPa,频率为30 Hz的余弦地震波。然后通过UDEC软件进行计算。图5~图12是多次加载下岩体的变化响应。
通过分析破坏过程,可以看到当进行第一次加载时,最外层的三个岩块已经发生了轻微的滑移,内部岩体由于外层岩体的约束作用,基本上处于稳定状态,而且靠得比较紧密,没有出现大的分离。当进行第二次加载时,可以看到最外层岩块发生了较大滑移,靠里一层的顶部也稍有下陷。第三次加载作用下,这两层岩块破坏趋势进一步明显。当进行第四次加载时,边坡基本发生滑移破坏,最外层岩块纷纷掉落。从整体的位移云图也可以看出,随着荷载作用次数的增加,边坡整体位移增大,只不过最外层的位移增长要明显快于边坡内部。同时还可以看出,带有节理的岩质边坡发生滑移破坏时,会形成明显的滑移带。
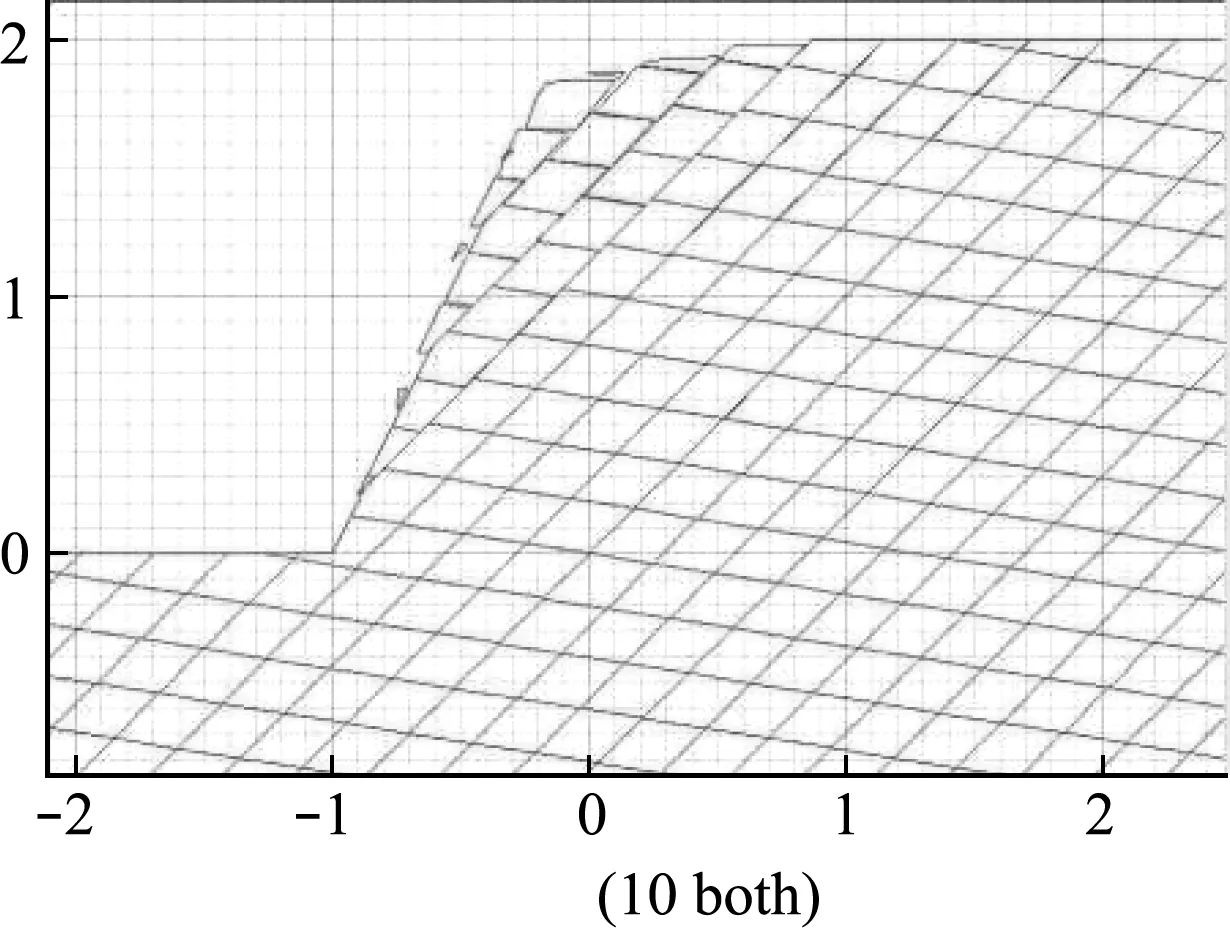
图5 第一次加载破坏
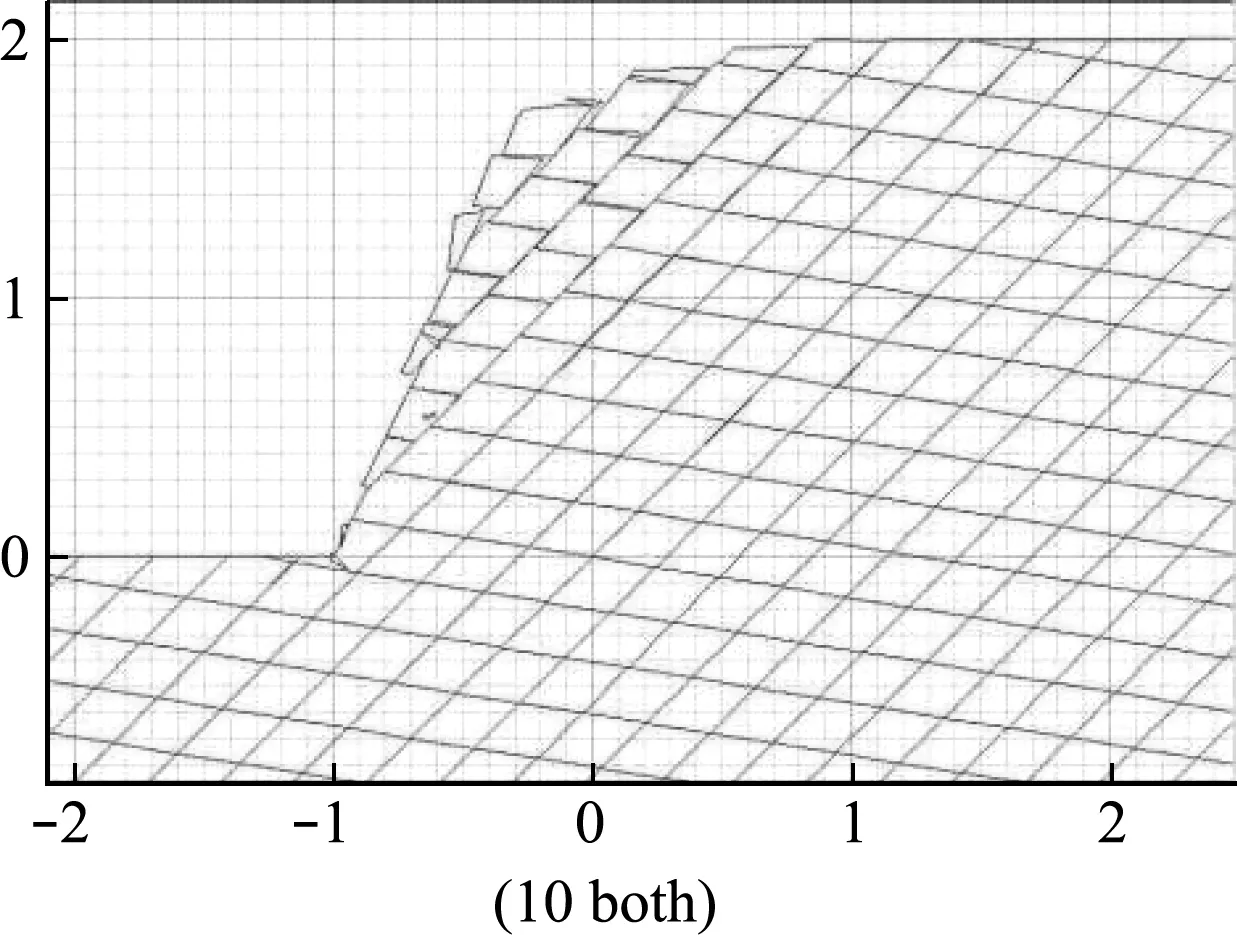
图7 第二次加载破坏
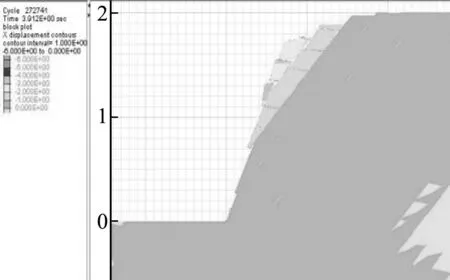
图8 第二次加载位移
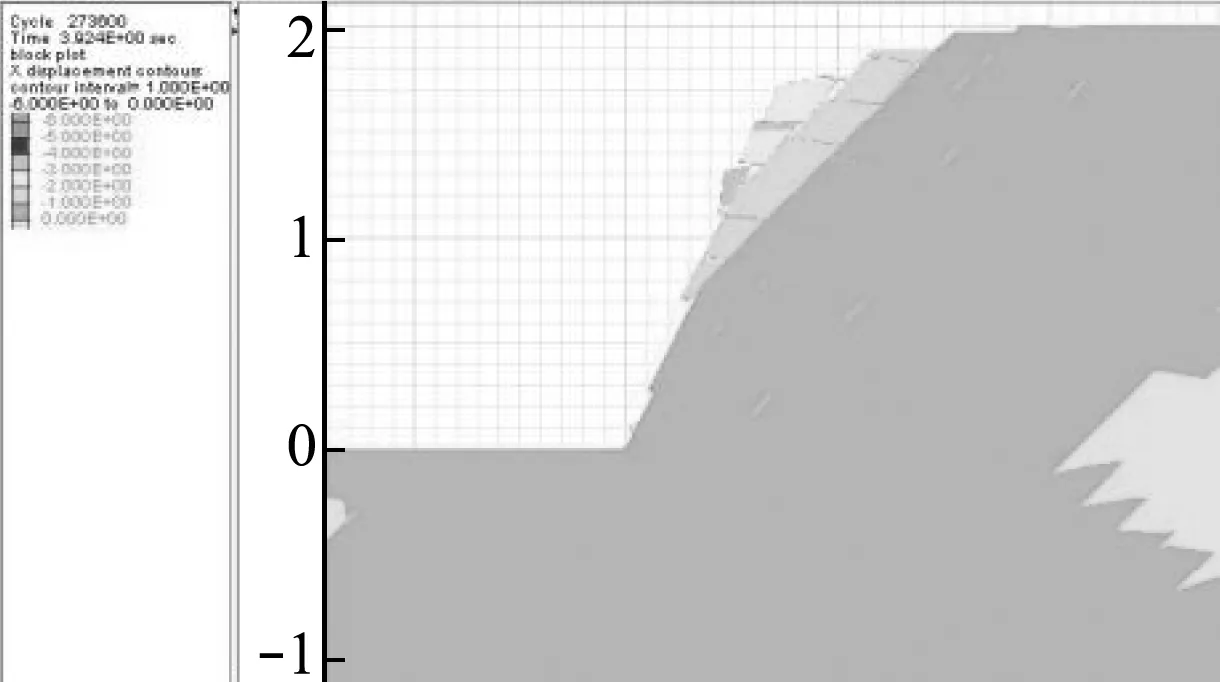
图10 第三次加载位移
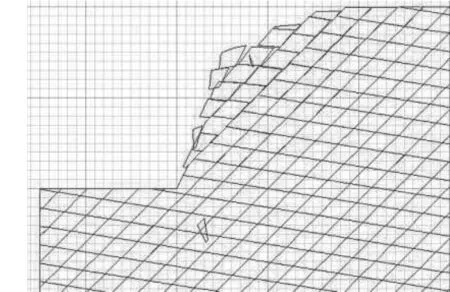
图11 第四次加载破坏
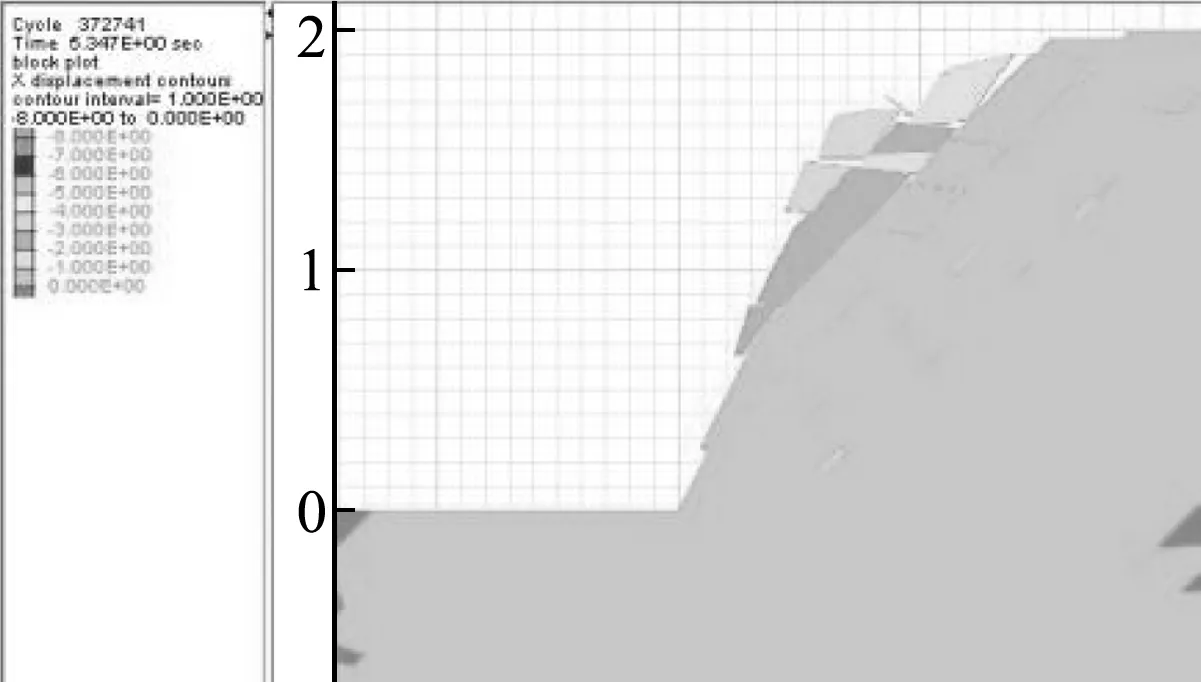
图12 第四次加载位移
4 拓扑特征的选择及持续同调与边坡破坏关联性的建立
4.1 特征选择
为了在支持向量机中实现拓扑方法,本文参考文献[15]的11条条码图统计量来表征边坡的拓扑结构信息。从贝蒂0和贝蒂1条码信息中选择不同的统计量表征边坡类型特征信息。条码的长度和位置值以埃为单位。
4.2 持续同调与边坡破坏关联性的建立
得到了边坡在地震荷载作用下的动态破坏过程以后,接下来就要找到以上有代表性的几个时刻,找到土颗粒的质心坐标,用Javaplex进行计算,并绘制条码图。
第一次加载时的破坏图可以看出外层岩体出现了微小滑移,内部岩体基本处于稳定状态。通过观察对应的条码图,发现0维贝蒂数大多在1附近,少部分超出了1。说明在地震载荷的作用下,最外层岩块发生松动,位移有所增大。再看1维贝蒂数,线条多且持续时间短,第一次加载时,岩块之间靠得相对紧密,围成的孔洞较小。

表3 支持向量机中使用的拓扑特征
从第二次加载的条码图可以看出,相对于第一次加载,最长贝蒂1有所变长,同时线条更稀疏。这说明部分细裂纹已贯通合并,形成数量较少但更宽的宏观裂缝。
0维贝蒂数增长,说明边坡的岩块整体上发生了松动,位移有所增长。1维贝蒂数仍然较为稀疏,贝蒂1最长值起于1.35,止于2.1,长度为0.75,最长贝蒂1长度有所增长。比较图13和图14可以看出,对边坡裂隙起主导作用的最长贝蒂1的终止值迅速后移,长度也变长。说明决定边坡最终稳定性的主裂隙宽度迅速增加,此时边坡整体上已经处于临界失稳状态。
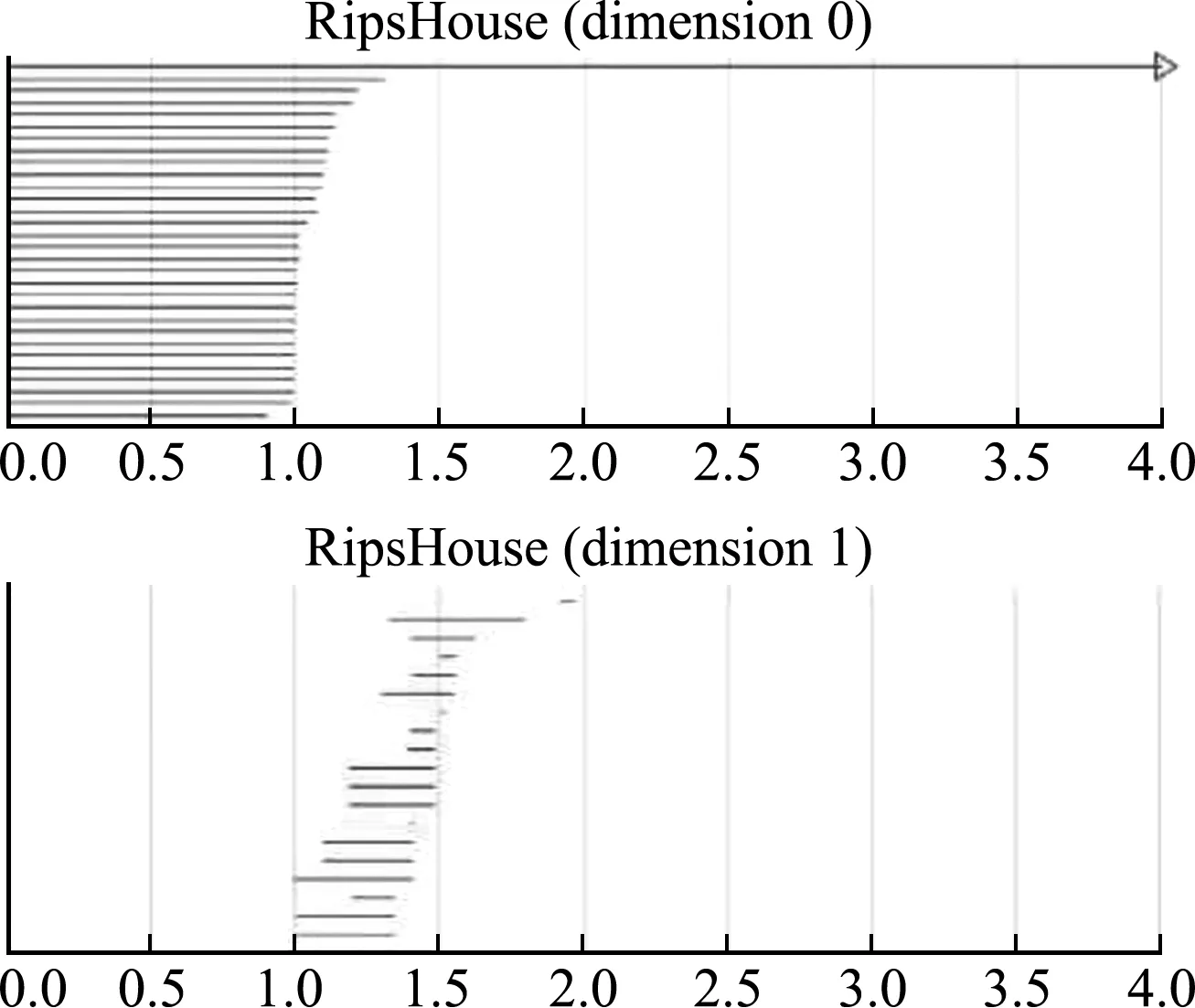
图13 第一次加载条码
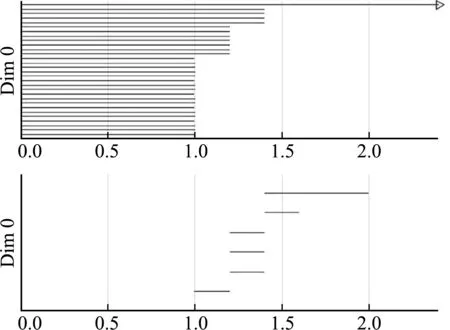
图14 第二次加载条码
从图16可以看出,0维贝蒂数条码底部增长明显,顶部基本维持在1.5~2.5。1维贝蒂数中相比于图15根数基本没变,但底部的几根线条变长,说明随着第四次荷载的作用,孔洞数没变,但是原来较小的孔洞有所变大。同时较远处出现了一个持续时间较短的线条,1维条码发生突变,说明边坡此时形成了更大的孔洞。边坡此时发生了滑移破坏。
现分别就4个过程的贝蒂0和贝蒂1的条码,选取几个有代表性的特征,即特征5、特征6及特征8进行分析。原则上,特征选取是根据其每个特征所反映的侧重点的不同,结合边坡这类工程特征实际,选取最能反映其变化过程以及本质的特征。之所以选这三个特征,是因为通过对比上述拓扑特征可以发现,它们有一个共同的特点,即都与边坡的裂缝有关,而裂缝是决定边坡稳定性的最关键的因素。特征5反映主裂缝的持续时间以及变化特征,特征6反映边坡的最大主裂缝的大小及变化趋势,特征8反映边坡整体的裂缝发育水平。
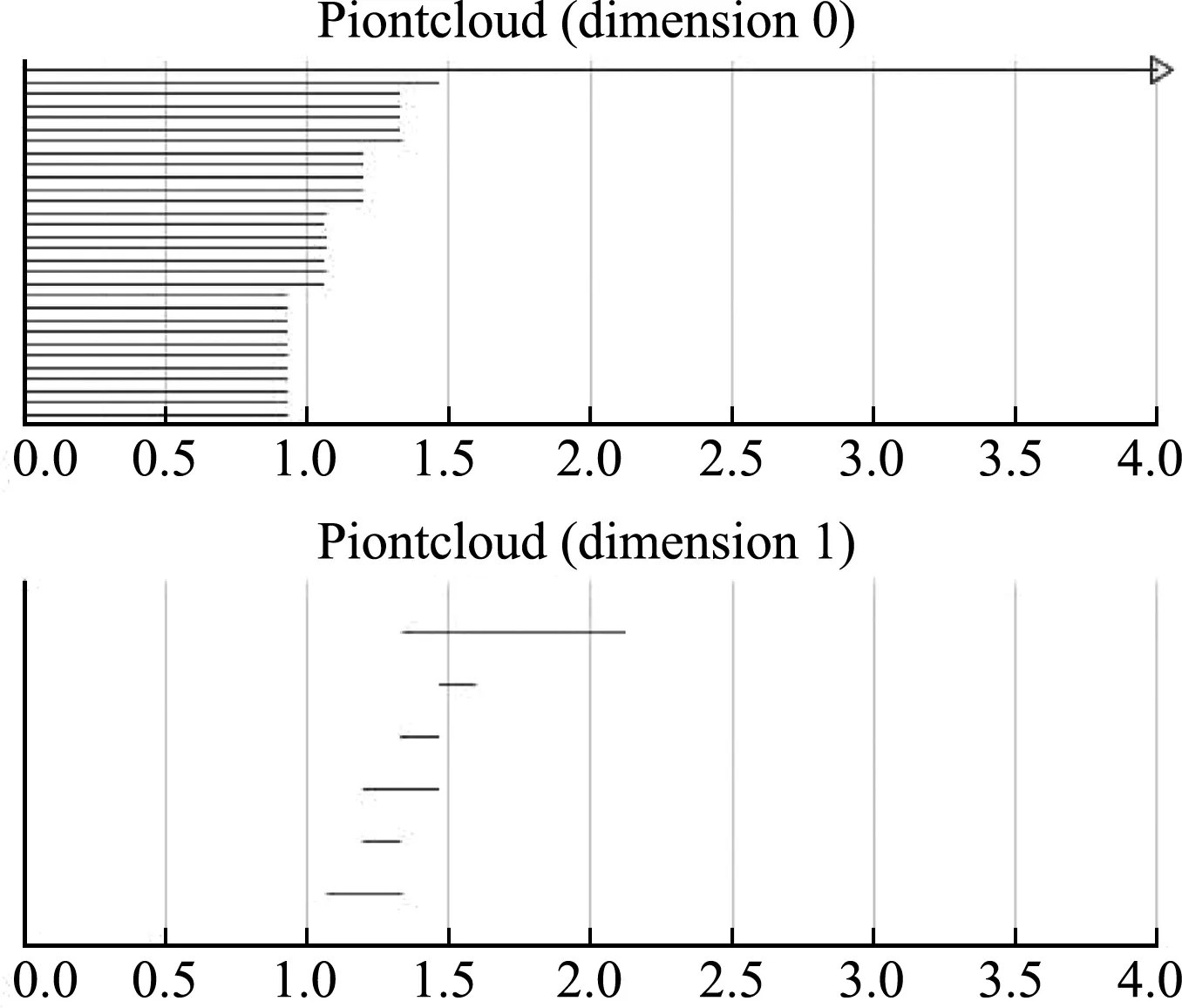
图15 第三次加载条码
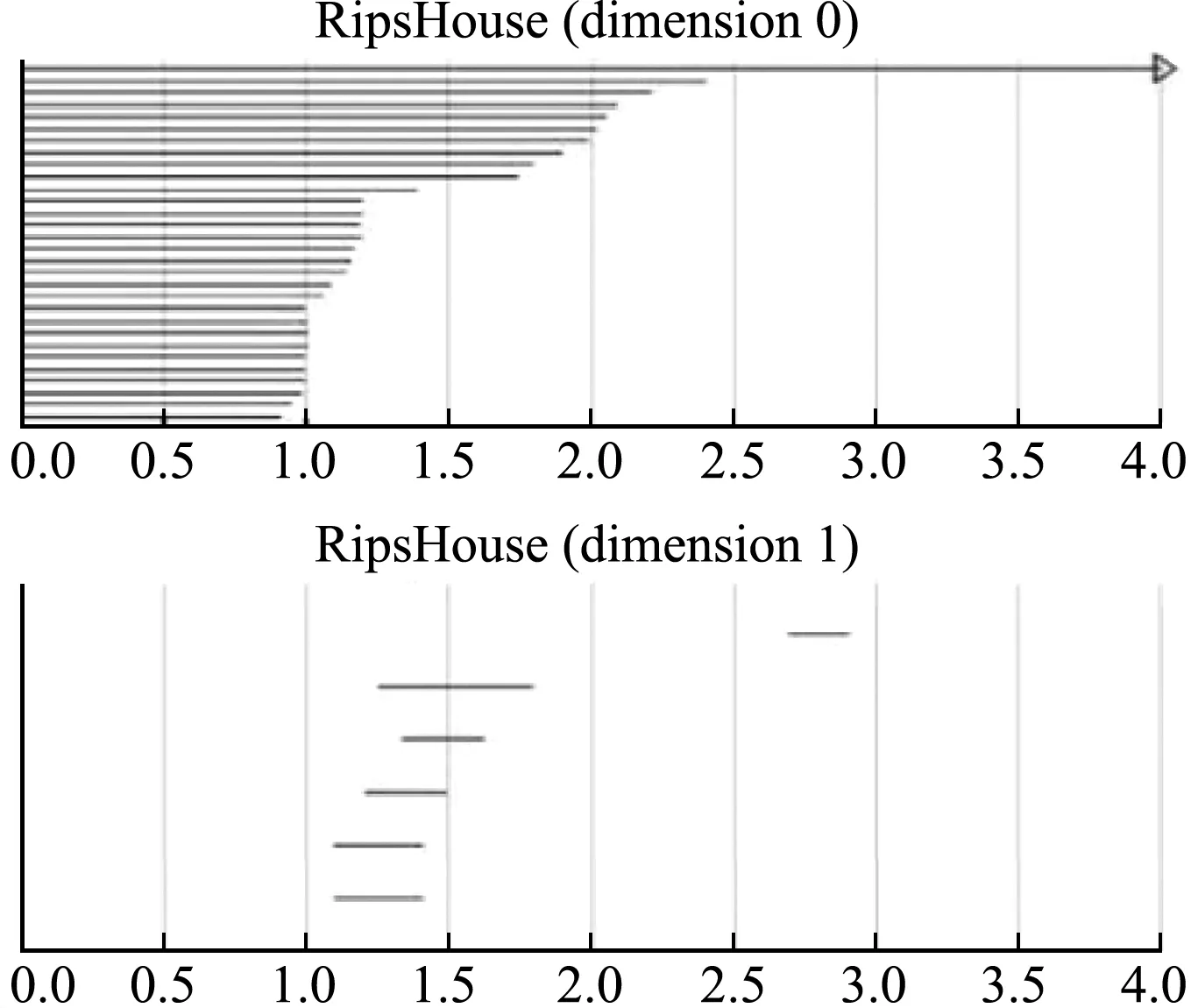
图16 第四次加载条码
首先是特征5,它的内容是最长贝蒂1的起始值,其反映的拓扑特征是最长环形成时的过滤值,即最大的裂缝从开始形成到完全破坏的持续时间。这四个时刻的最长贝蒂1的起始值分别为1.35,1.4,1.35,1.2,终止值分别为1.75,2,2.1,1.75(均按时间增加顺序排列)。现将起始值和终止值用折线图的形式表达出来,便于观察其变化规律。折线如图17和图18所示。
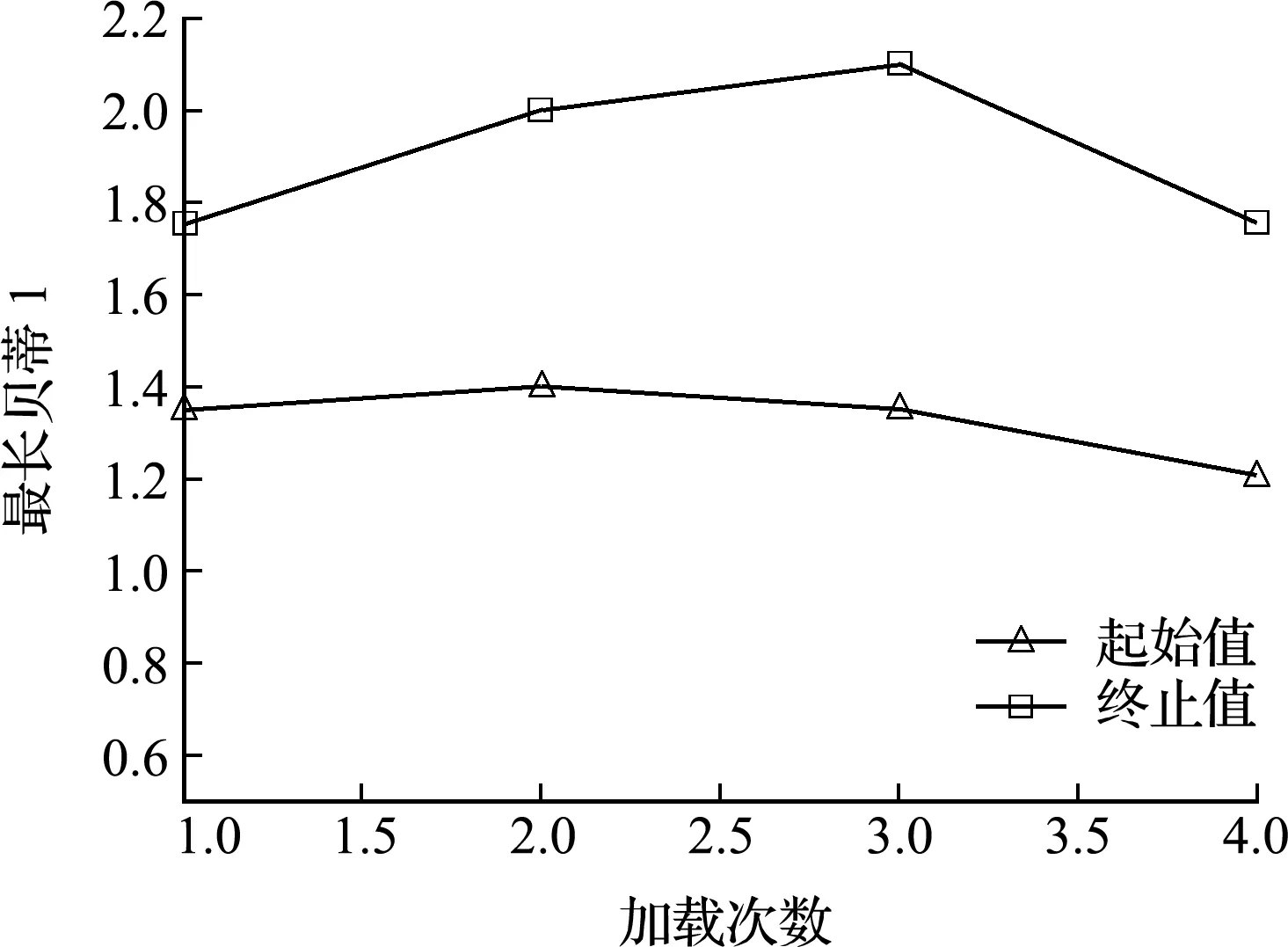
图17 特征5折线
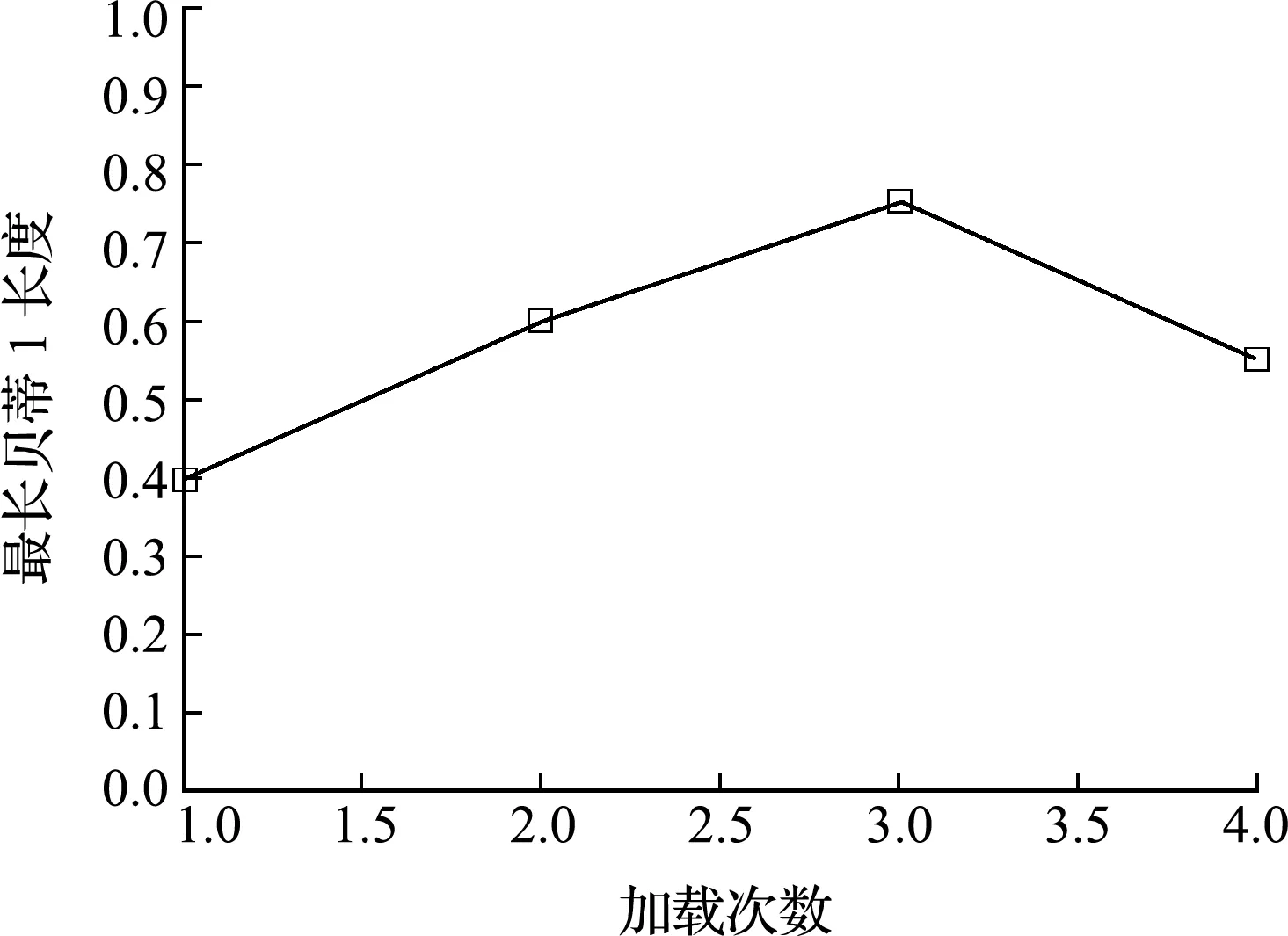
图18 特征6折线
可以看出,最长贝蒂1的起始值和终止值开始均有所增加,只不过终止值增加更快,且在第三次加载时达到峰值,然后迅速下降。而起始值开始略微增加,在第二次达到拐点,然后逐渐减小,但变化趋势较终止值更慢。这种趋势反映出边坡里的裂缝逐渐变大,而且有着整体往宽扩张的趋势,直到第三次加载时,达到峰值,边坡也处于临界状态,即将发生失稳滑移破坏。
接下来分析特征6即最长贝蒂1条码的长度,最长贝蒂1表示最大的孔洞的持续值。而最大孔洞即最大主裂缝,决定着边坡最终的稳定状态。可以看出,最长贝蒂1从初次加载时的0.4逐渐增加,到第三次加载时,达到峰值,此时边坡处于临界状态。第三次加载后,长度越过最大值 0.75,开始逐渐减小。这说明主裂缝在第三次加载时达到最大,之后边坡发生失稳破坏。这与前面结合条码图分析得出的结论一致。
接下来分析特征8所表达的拓扑特征。折线如图19所示。特征8反映的拓扑特征是边坡的平均裂缝宽度。可以看出,最长贝蒂1的平均长度从初次加载开始就逐渐增加,只不过速度比较平缓。而第三次加载后,曲线开始迅速上扬,说明第三次加载时的边坡状态是演变过程中的一个拐点。这说明开始时边坡整体裂缝增长缓慢,直到荷载加载到第三次时,边坡达到临界状态,越过这一状态,边坡整体上裂缝迅速发展,随即发生了失稳破坏。
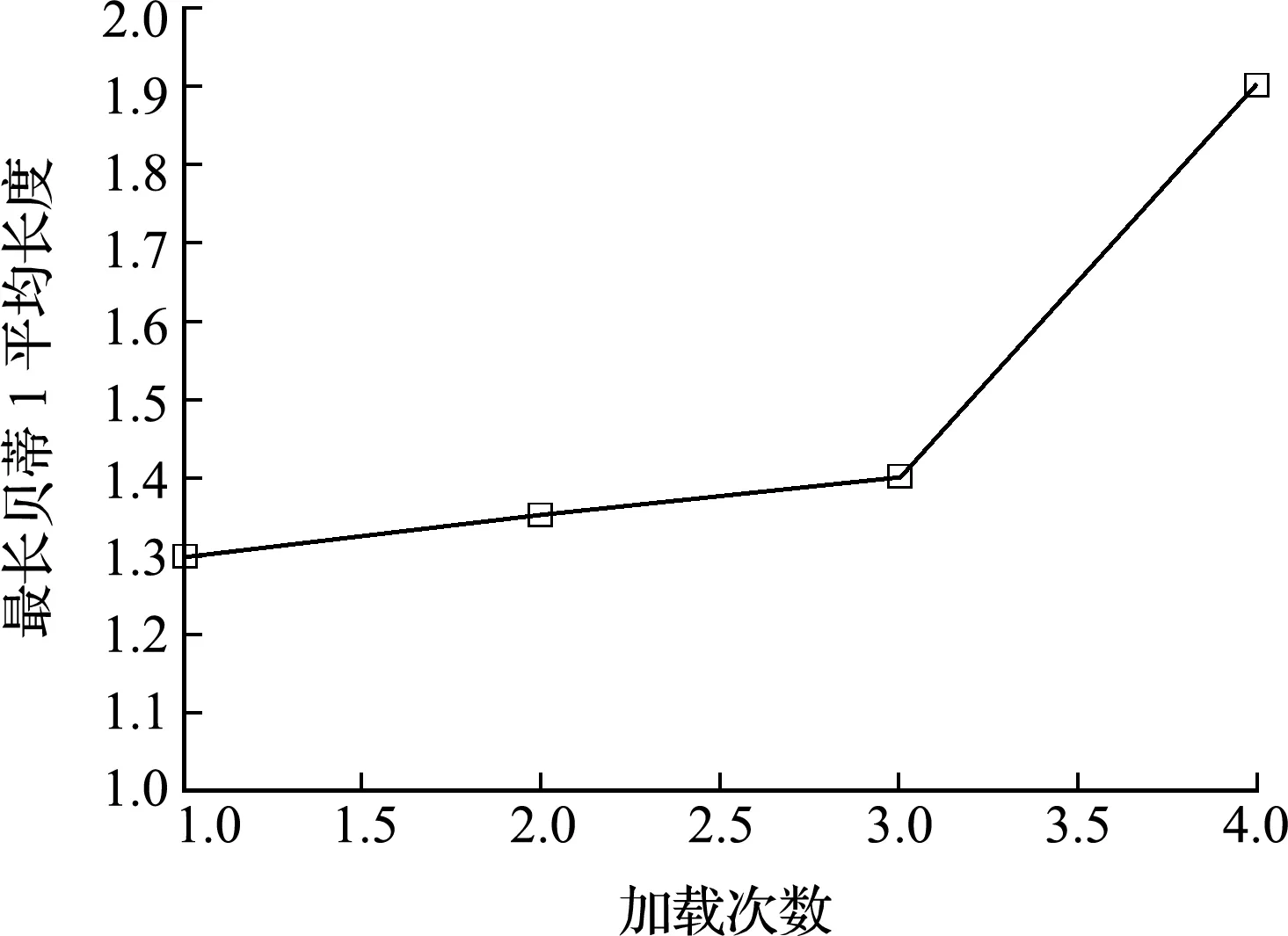
图19 特征8折线
5 总 结
从以上模拟可以看出,基于支持向量机理论的持续同调特征选择可以很好地解释边坡的变化过程以及拓扑特征,主要结论如下。
(1) 将一种全新的数学方法,即持续同调,引入边坡安全设计与灾害预报研究领域,通过外载荷作用下边坡的破坏特征研究,证明持续同调用于边坡工程领域的可行性和准确性。
(2) 基于离散元法得到边坡在载荷作用后的动力响应和裂缝演化过程,运用持续同调数学方法对边坡的破坏特征进行研究。结果表明,随着荷载的持续作用,0 维贝蒂数发生少量变化,即外力改变了土颗粒结构分布,0 维e整体呈现变大趋势,反映出了边坡在完全失稳前逐渐松动,且从 1 维贝蒂数的孔洞数可以看出,最长贝蒂1条码的长度表示拓扑特征中最大孔洞的大小,决定了边坡的演变特征和失稳过程,因而是所有特征中最能直观反映边坡破坏程度的。
(3) 贝蒂1条码的突变意味着边坡发生了失稳破坏,所以可以通过条码图特征对边坡失稳进行预测。利用探测雷达等手段扫描边坡的内部几何结构,即可用持续同调的方法对其进行拓扑特征分析,还可以将数据用到支持向量机和BP 神经网络等机器学习领域,即可对边坡的防护工程设计和评估进行智能化且精确化研究,这为边坡安全设计与灾害预报研究提供了一种全新的思路。
