一种求算结构可靠度指标的新方法
2021-04-30张泽俊余颖烨刘敬敏
夏 雨, 张泽俊, 余颖烨, 刘敬敏
(广西科技大学 土木建筑工程学院,柳州 545006)
1 引 言
在结构分析中,材料、载荷和几何特性都存在不确定性。因此,为了对工程结构进行有意义的分析,必须考虑不确定性[1-3]。结构可靠性理论是将不确定性影响引入分析过程的工具[4]。
在可靠度计算问题的分析中,工程的失效概率可归结于多元变量区域积分问题,通常涉及到随机变量的多维积分会使计算非常困难,特别是在大而复杂的结构或具有低失效概率的结构中。而一般的模拟方法通常很费时费力[5]。将功能函数线性化的一次二阶矩法(JC法)应用在工程结构可靠性计算中公认为一种有效的方法[6],但其只适用于功能函数非线性较低的情况,非线性程度较高时,该方法往往不收敛,给结构的可靠性分析带来困难。
为了实现可靠度及结构最可能失效的设计点MPP有效而快速的求解,None[7]提出该点位于极限状态曲面上,它与标准法向坐标系或u-空间(所有变量的均值和标准差)之间的距离最小。设计点到原点的距离称为β表示的可靠性指标。利用β的几何意义,将可靠度求解归结于求解含约束的最优问题[8]
(1)
式中Y=(y1,y2,…,yn)Τ为标准正态分布的随机变量,Y*为设计点,G(Y)为结构的功能函数。G(Y)<0和G(Y)>0分别为结构的失效域和安全域,G(Y)=0为极限状态面。
对此Hasofer等[9]根据基本随机变量的分布信息扩展了迭代公式,提出HLRF法,但还没解决极限状态函数非线性程度高时迭代不收敛的问题。Zhang等[10]提出用Armijo算法和Wolfe条件来选择步长的改进HLRF法(iHLRF法),Keshtegar等[11,12]提出通过使用松弛HL-RF拟合二阶函数来提高FORM公式的鲁棒性,同时引入共轭梯度法提高HLRF法的收敛速度。周生通等[13]提出一种新的搜索准则,利用已有信息估算计算参数的aHLRF法,实现自适应计算可靠度指标,收敛性得到保证。但这些算法对初始参数的选取敏感性较高,不同的初始参数值对迭代速度影响较大。
贡金鑫等[14,15]在迭代点沿负梯度方向以一定的步长限制迭代的发散,提出有限步长法,但该方法在初始步长选择不当时并不能收敛。对此吴狄等[16]提出自动变步长的搜索方法,避免了步长的试算,但该方法相对在收敛速度方面有一定影响。周凌等[17]引入黄金分割法求解合适的步长,但同时引入更多的初始参数,增加了收敛的不确定性。
本文在可靠度指标β的几何意义的基础上,提出一种新的求解可靠的指标和设计点的方法。该算法不同于有限步长法和HLRF法的步长搜索方式,采取曲面搜索,不需要预先设置初始参数,简单有效,具有较强的鲁棒性。
2 算 法
2.1 算法原理
本文在求解式(1)时,由于目标函数的特殊性,使用针对性的方法而不依赖于现代优化方法。式(1)可理解为在标准正态空间中,求一最小值β,以β为半径,以标准正态空间的坐标原点o为球心的超球体相切于极限状态面。当可靠度指标收敛时,如图1所示,点y*和原点o的连线I必与极限状态面正交,即线I与极限状态函数在y*处的法向量n共线,根据此特点,本文提出一种求解可靠度思想,该思想分为两部分,一是当超球体与极限状态面相离时,迭代点在安全域中向极限状态面靠近,可靠度指标β增加,该过程即是超球体的扩张过程,一直持续到超球体与极限状态面相切或相交;二是当超球体与极限状态面相交时,沿极限状态面搜索求得另一设计点,该设计点相对上一迭代点与原点o的距离更小,可靠度指标β减少,该过程即是超球体的缩小过程,一直持续到超球体与极限状态面相切,得出最终的验算点和可靠度指标。
2.2 计算方法
根据此思想,提出以下计算方法:
设X=(x1,x2,…,xn)Τ是与设计问题相关的n个原始随机变量的向量,分布函数为Fi(xi)(i=1,2…,n)。设X表示的结构功能函数为
ZX=G(X)
(2)
在变量X的随机分布空间中,变量X与之对应的等效标准正态空间(Y空间)的变量Y的函数关系为
(i=1,2…,n)(3)
结构功能函数对应于Y空间有

图1 二维标准正态空间下设计点与极限状态面关系
ZY=G{F-1[Φ(Y)]}=gY(y1,y2,…,yn)
(4)

β(k)=‖y(k )‖
(5)
该点在极限状态函数上的梯度矢量为
(6)
(1) 当y(k )在极限状态面的安全域时,g(y(k ))>0。下一迭代以负梯度方向靠近极限状态面,即
g(y(k + 1))=g(y(k )-α(k )gY)=0
(7)
式中α(k )为迭代步长。在下一迭代点用泰勒级数展开,并取一次项:
(8)
求解式(8)可得步长
(9)
下一迭代点为
(10)
(2) 当y(k )在极限状态面时,g(x(k ))≈0。有经过该点的切平面,方程为
Q(Y)=(y-y(k ))ΤgY=0
(11)

(12)
(13)

(14)
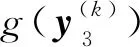
(15)

(16)

(17)
下一迭代点为
(18)
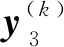
(19)
式中λ∈(0,1)。对λ的求解,其实是简单固定方向的一维线性搜索,即对于该类问题一般可以用黄金分割法、二分法和最速下降法或Newton法等方法均可有效求解。也可展开泰勒级数一次项,有
(20)
求解式(20)得
(21)

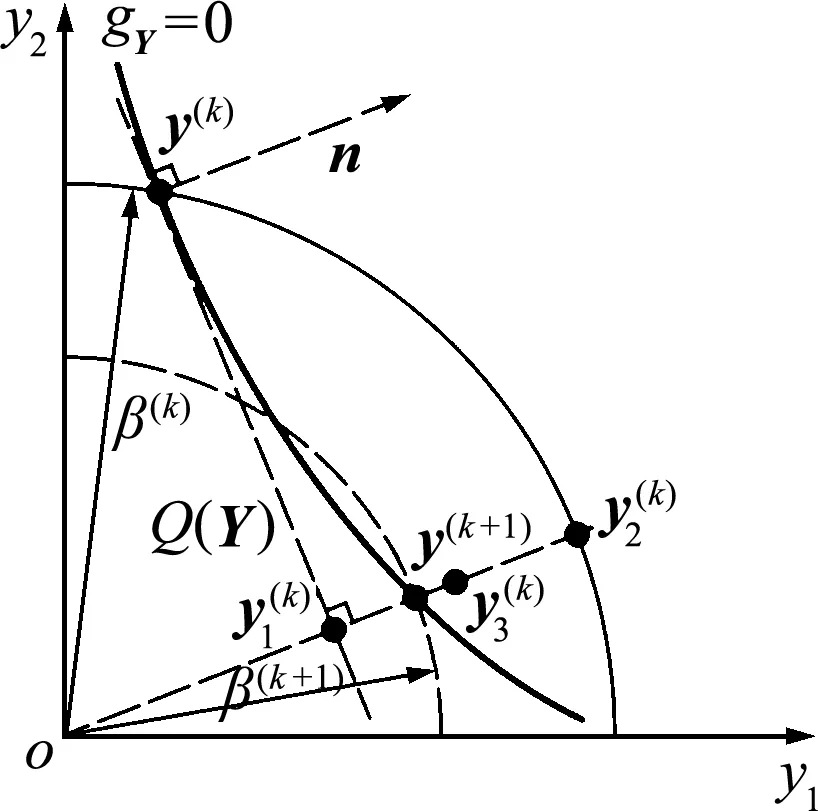
图时迭代过程

图时迭代过程
内循环过程。经验表明[6,13,18],取ε2<1e -5即可保证点y(k + 1)基本在极限状态面上。
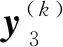
‖y(k + 1)-y(k )‖<ε
(23)
式中ε为收敛精度,可取ε=0.001。
2.3 算法迭代步骤
综上所述,迭代步骤如下。
(1) 将原始随机变量X空间替换为等效标准正态Y空间。
(2) 选取初始点y(0)(一般取均值点),精度ε>0,ε1>0,ε2>0,k=0,t=0。
(3) 由式(10)得点y(k ),k=k+1。
(4) 检验y(k )是否满足g(y(k ))<ε1,若满足,转步骤(5);否则,转步骤(3)。
(7) 由式(15,17)求解β(k + 1)。
(8) 由式(18)求得y(k + 1),k=k+1。
(9) 检验是否满足式(23),若满足,停止迭代,由式(5)得到β;否则,转步骤(5)。

(11) 由式(21)求得步长λ,并由式(19)得到y(k + 1),t=t+1。

3 数值算例
算例1和算例2选自文献[15],收敛精度取ε=0.001,本文方法ε1取0.001,ε2取1×10-5。
算例1设结构的极限状态函数为
式中x1和x2为相互独立且服从正态分布的随机变量,且x1~N(3.0,1),x2~N(2.9,1)。将原始正态变量x1和x2转化为标准正态变量y1和y2,其对应Y空间的功能函数为
gY(y)=(3.0+y1)3+(2.9+y2)3-4.0
JC法和本文方法的外循环迭代过程如图4所示,可以看出该算例的非线性程度还是比较高的,JC法和HL-RF法无法收敛。但是使用本文的方法,却可以平稳收敛。由表1可知,本文方法的外循环迭代次数8次,相对于其他方法,本文方法的迭代次数大大减少;内循环迭代7次,此过程为一维固定方向的寻优过程,其他方法则是步长的调整过程。较其他方法,本文在此环节上是比较轻松的。文献[14]的有限步长法不需要进行内循环,但取不同参数时迭代次数会大幅度增长,如取步长调整系数为1.2,则步长取为5时需迭代280次才能收敛,取步长为10和2时则不收敛;取步长为1时,取步长调整系数为1.3需要39次才能收敛,取步长调整系数为1.5需22次才收敛。文献[10]的iHLRF法和文献[13]的aHLRF法同样受参数干扰很大,不同的参数对其内循环和外循环有较大的影响。如图5所示,本文方法取外循环部分,同 JC法和有限步长法相比有更高的稳健性。

图4 算例1的迭代点分布

图5 算例1的可靠度指标迭代分布
本文方法最终验算点为(-1.7269,-1.6536),该点与原点的连线和极限状态函数在该点处的法线夹角θ=0.0144°,功能值为g(y(8))=3.0119×10-7,而文献[15]方法的夹角θ=0.127°,θ值越小,计算结果的精度越高。说明本文方法在相同精度下,能够得到更接近精确验算点的迭代点。本文方法在精度和效率上都有足够的优势。
算例2设结构的功能函数为
GX(x)=(1/P)ln{exp[P(1+x1-x2)]+
exp[P(5-5x1-5x2]}
式中x1和x2服从标准状态分布且相互独立。P为该功能函数的参数,当取P不同值时,极限状态面如图6所示,极限状态函数的非线性随P值增大而提高,可以看出,在P=1和10时,验算点附近的都有很高的非线性。
算例2使用JC法和HLRF法都无法收敛,本文提出的方法则表现良好,计算结果列入表2。

表1 算例1计算结果

表2 算例2计算结果Tab.2 Results of example 2
aHLRF法较iHLRF法有更高的效率,本文方法与aHLRF法对比可知,本文的方法在极限状态函数的非线性越高时,效率上的优势更明显,当P=10时,本文方法的迭代速度是aHLRF的十几倍。本文方法的不足之处在于内循环的迭代次数较多,但可以通过其他寻优方法解决,精度一致时,并不影响外循环的迭代次数和结果。
有限步长法选择不同的参数有不同的收敛性和收敛速度,取步长为1,当P=1时迭代17 次,θ=2.3740°,P=10时迭代36次,θ=13.91°,本文方法计算的结果精度更高。迭代过程如图7和 图8 所示。可以看出,本文方法的迭代更稳健,且并不会因为功能函数非线性程度高而分散迭代点。
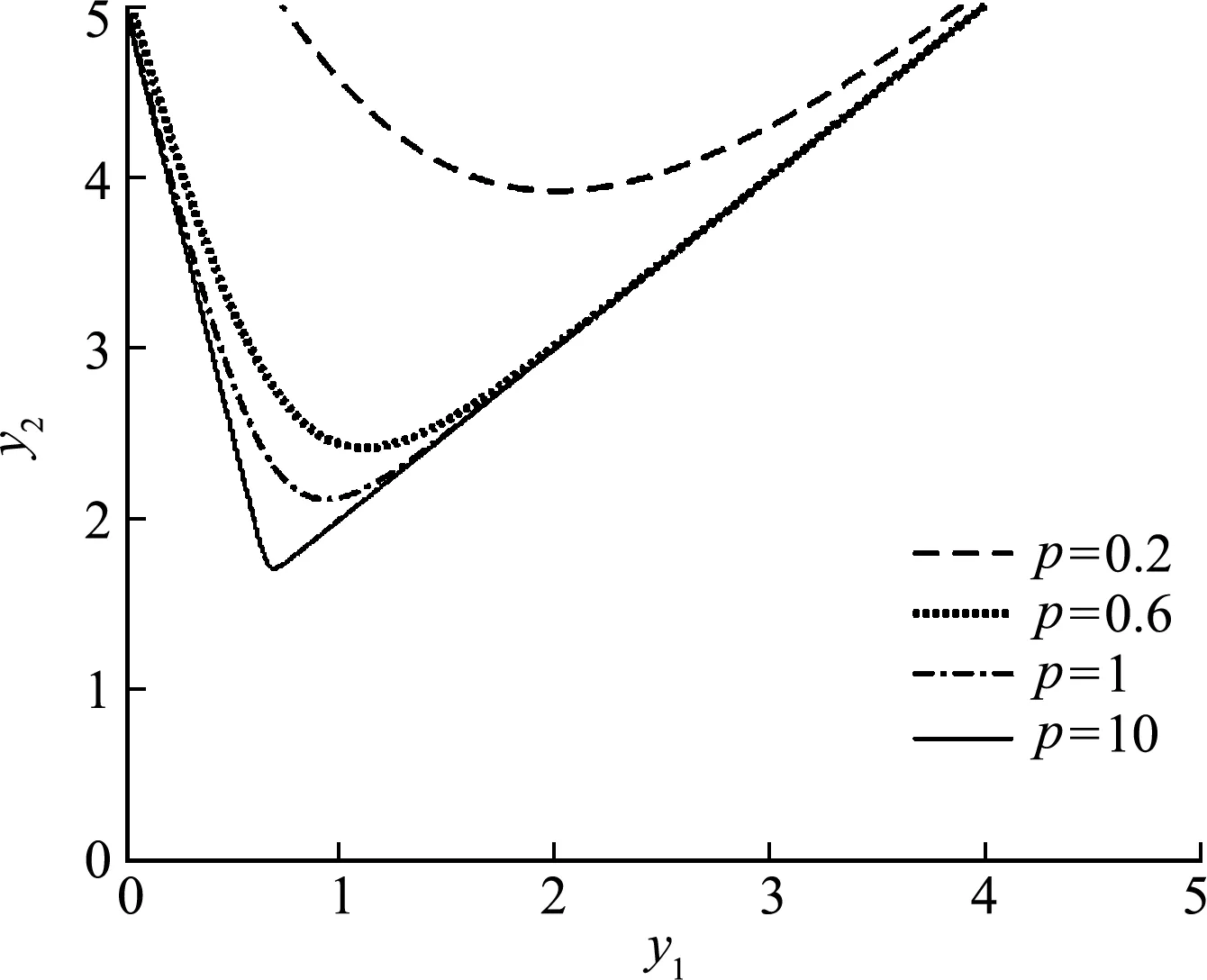
图6 算例2中不同P值对应的失效面

图7 P=1时的迭代点分布
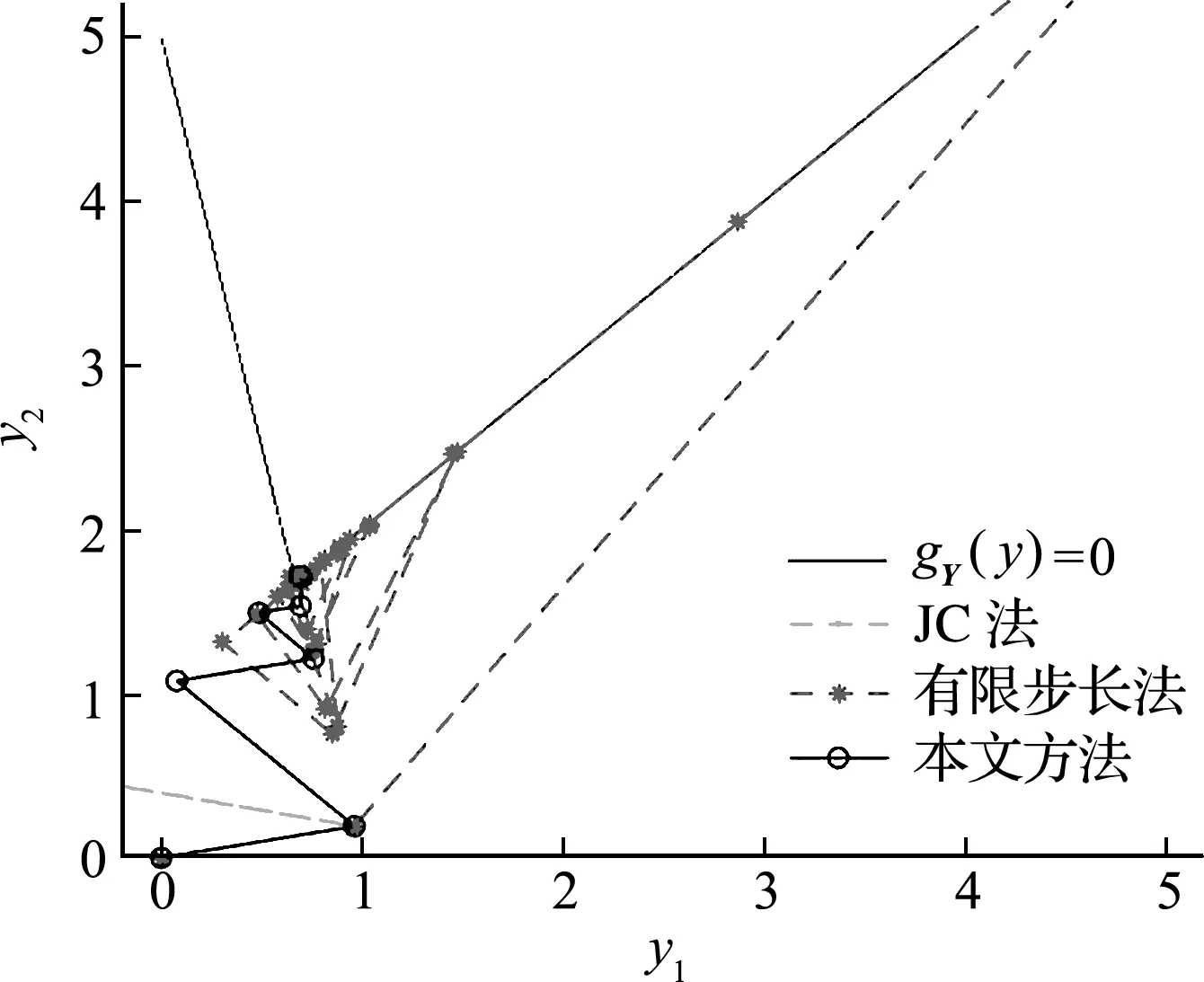
图8 P=10时的迭代点分布
4 结 论
在可靠性分析中,JC法是一种推荐和广泛使用的确定可靠度指标和工程设计点的方法,但该方法在结构功能函数非线性程度较高时容易不收敛。本文提出一种新的迭代算法,该算法通过沿曲面搜索得到更合适的设计点来保证收敛性。这里迭代点的位置是由辅助点控制的,不需要通过步长的调整来保证收敛,因此可以避免其他算法对初始参数的尝试过程和不同的参数带来的收敛效率的影响。算例表明本文方法具有良好的收敛速度和计算精度,特别在结构功能函数非线性高时很有效。在具有高非线性的大型复杂结构工程的设计点计算和可靠性分析中有很好的应用前景。
