高精度近场动力学方法：一维键型研究

吴 凡， 段庆林

(大连理工大学 工业装备结构分析国家重点实验室，大连 116023)

1 引 言

近场动力学PD(Peridynamics)模型是由Silling[1]提出的一种新兴的非局部连续体理论，其以积分方程取代微分方程，允许位移场出现间断，能够对连续和非连续问题作统一处理。因此，PD对断裂破坏问题的分析模拟十分方便有效[2]。

PD分为键型[1]和态型[3]。其中，键型PD模型简单且计算速度快，不仅应用于各种工程问题，如水下爆破破冰[4]和边坡失稳[5]等，还广泛应用于各种新型材料的分析，如功能梯度材料[6]、复合材料[7]以及热电材料[8]等。然而，PD的计算精度还有待进一步提高[9]，主要是由于积分方程中的区域积分不能得到精确计算以及边界附近键缺失导致的边界效应。

针对积分误差问题，已发展了多种修正方案。体积修正法[10]对具有不完整影响域的物质点积分给出了以键长为自变量的修正公式。HHB修正方案[11]根据积分区域与网格单元重叠的不同情况分别计算，进一步提高了积分的准确性。Seleson等[12]提出了PA-AC修正方案，能更精确地积分圆形影响域，但计算代价较高。Liu等[13]通过构建PD与传统连续介质力学之间关于应力与弹性模量的等价关系，为PD建立了新的微模量，并称之为数值微模量，发现采用数值微模量能够显著提高计算精度。

边界效应问题是由于边界粒子影响域的残缺导致键缺失，虚假地降低了边界附近的刚度[14]。针对该问题，Bobaru等[15]根据边界处物质点的体积修正了键刚度。Madenci等[16]采用力密度法和能量法重构边界附近的应变能密度，得到了相应的修正系数。Macek等[17]基于虚位移原理引入了刚度修正系数。章青等[18]通过修正边界处的微模量修正边界效应。虚拟节点法[19]是目前应对该问题的主要方法，通过在边界外侧布置虚拟节点，弥补了边界点影响域的残缺，有效改善了边界效应问题。然而，边界条件需要施加于虚拟节点，且需要根据不同的边界条件对虚拟节点的位移进行相应的特殊操作，实现起来较为繁复。

本文以一维键型近场动力学为研究对象，对上述两个导致PD精度不高的问题分别发展了改进方法。针对区域积分问题，本文遵循了数值微模量方法[13]的思想，但提出了根据应变能密度而非应力的等价关系对微模量实施修正。而且，本文方法无需进行体积修正，更为简单直接。针对边界效应问题，提出了建立位移和力边界虚拟键的方法，无需布置虚拟节点，有效简化了方法的实现。

2 一维键型近场动力学模型

近场动力学的控制方程为

(1)

(2)

PD一般采用规则分布的节点(node)进行空间离散[21](一维情况如图1所示)，优点是计算速度快，但计算精度还有待提高。离散后，式(2)可写为

(3)

式中Δx为格子间距(grid spacing)。显然，距边界不小于δ的节点(图1的实心圆点)影响域完整，而边界附近的节点(图1的实心方点)影响域不完整，发生键缺失，导致边界效应。

图1 一维近场动力学空间离散

3 高精度近场动力学方法

为提高近场动力学的计算精度，本文针对一维键型PD的微模量和边界效应分别发展了改进方法。

3.1 基于离散应变能等效的微模量修正

PMB材料的一维键型PD在均匀拉伸下粒子的应变能线密度为

(4)

式中w=0.5cs2ξ为键的微势能。相同情况下，经典连续介质力学理论中一维杆的应变能线密度为

(5)

式中E为弹性模量，ε为线应变，A为杆的横截面积。注意到此种情况下有s=ε，则通过式(4，5)的等效可得到PMB材料的PD微模量[20]

c=2EA/δ2

(6)

应指出的是，上述等效的前提是式(4)的积分得到精确计算。然而，在离散情况下，由于数值积分的不准确，直接采用式(6)将导致较大误差。

针对该问题，本文提出的解决办法是在上述等效中采用离散而非连续情况下的PD应变能密度。考虑受均匀拉伸的一维PD模型，任意粒子的应变能密度为该粒子所有键的微势能之和，即

(7)

(8)

式中m=[δ/Δx],[]表示向下取整。将式(8)代入式(7)可得

(9)

再通过式(9)与式(5)的等价即可得到修正的微模量

(10)

后面的数值算例结果将表明，采用式(10)的修正微模量将能显著提高计算精度。

3.2 边界虚拟键

边界附近粒子会由于影响域残缺造成键缺失，进而导致边界效应。本文处理该问题的总体思路是通过建立边界附近粒子与边界之间的虚拟键来弥补这些粒子的键缺失，从而改善边界效应，分为固定边界和力边界。

3.2.1 固定边界

固定边界指的是将一维杆的端点位移固定为0。在PD方法中，该条件的实施通常是将离端点最近的粒子位移固定为0。由于边界效应的存在，这会导致端点附近区域位移和应变的较大误差。本文将通过增加边界虚拟键来改善边界效应，然而该虚拟键的大小如何确定仍然未知，这关系到固定边界条件是否能够得到精确施加。注意到，结构和载荷均对称时一维杆的中心点处位移恒为0(如 图2 的杆B)，这为确定虚拟键的大小提供了思路。

考虑图2杆A的PD求解，其左边界x=xL为固定边界。参照图2杆B，将杆A以左边界为对称面进行镜像映射，得到如图2杆C所示的虚拟对称区域，再基于此分析缺失的键(即由边界截断的键)，即可确定所需的虚拟键的大小。

(11)

其中

(12)

伸长率可由其定义写为

(13)

(14)

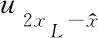
(15)

将式(15)代入式(12)，并将结果代入式(11)即可得到粒子x的固定边界虚拟键为

(xL

式(16)为连续情况下固定边界虚拟键的计算公式。空间离散后，式中连续积分通过离散节点求和计算，对于边界区域(图2的阴影区域)距离固定边界的第K个节点XK，其位移为UK，则其固定边界虚拟键为

(17)

在PD计算中，为所有处于固定边界区域的节点按式(17)建立边界虚拟键，能有效改善边界效应。

图2 固定边界条件施加方案

3.2.2 力边界

力边界的边界效应也是由边界区域粒子的键缺失导致。因此，类似于上文固定边界的处理方式，对力边界区域的粒子也通过建立边界虚拟键弥补键缺失，改善边界效应。与处理固定边界不同，虚拟键的大小不由对称关系导出，而是基于远离边界区域没有边界效应这一事实，详细阐述如下。

(xR

(0<γ<δ)(19)

(20)

由式(20)可求得伸长率

(21)

将式(21)代入式(19)得到距离力边界γ的粒子的力边界虚拟键为

(0<γ<δ)(22)

同样，式(22)也为连续情况下力边界虚拟键的计算公式。空间离散后，对于距离力边界第I个节点XI，其虚拟键应为

(23)

式中伸长率需由

(24)

计算得到

(25)

图3 边界力施加方案

将式(25)代入式(23)可得到节点XI的力边界虚拟键

(26)

4 数值算例

4.1 两端拉伸杆

如图4所示的1 m长杆，横截面积A=1 m2，两端受集中力F=5000 kN，材料密度为2400 kg/m3，杨氏模量为10 GPa。PD离散采用100个均匀分布的节点，并用动态松弛法[22]计算至准静态。

图4 两端拉伸杆件

经典PD方法和本文发展的高精度PD方法 hp -PD(high-precision PD)计算得到的应变沿杆分布如图5所示。可以看出，经典PD的结果边界效应明显，应变在杆两端区域发生剧烈的虚假震荡，远离边界区域的应变也严重偏离解析解，误差很大。本文通过实施微模量修正和边界修正发展的 hp -PD 方法得到的应变分布与解析解εe=5×10-4完全吻合，误差在10-25量级，达机器精度。为厘清两种修正方法各自的作用，图5还比较了对经典PD仅作微模量修正(标识为PD+c)和仅作边界修正(标识为PD+b)两种方法的数值结果。可以看出，两种修正方法的作用相对独立，一方面，微模量修正能显著提升远离边界处的计算精度，但对边界附近的虚假震荡无用；另一方面，边界修正能消除边界附近的虚假震荡，但不能改善内部区域的计算精度。因此，为全面提升PD方法的性能，需同时采用微模量和边界修正。

采用该算例进一步考察节点影响域大小对计算精度的影响。选取五种影响域，大小分别为δ=2Δx,3Δx,4Δx,5Δx,6Δx，并取杆中点处的应变与解析解作比较，结果如图6所示。本文的 hp -PD 方法在不同影响域下的计算结果均与解析解完全一致，成为机器精度下的解析解。标准PD的所有计算结果均严重偏离于解析解，误差很大。一方面，减小影响域，PD计算精度明显下降，这主要是由于影响域内积分点数目的减少导致了更大的积分误差；另一方面，即使对于最大影响域δ=6Δx的情况，PD的计算误差仍然达到10%左右，与本文的 hp -PD 差距甚远。继续增大影响域，PD的计算精度可得到些许改善，但同时也会导致计算量的急剧增大，因而不建议采用。

图5 两端拉伸杆应变分布比较

4.2 一端固定一端拉伸杆

该算例主要用于考察本文方法施加固定边界条件的准确性。仍采用上一算例的长杆，材料及数值离散均不变，只是将杆左端由力边界改为固定边界，如图7所示。经典PD和本文发展的 hp -PD 计算得到的应变沿杆分布如图8所示。与4.1节结果一致，经典PD导致了很大的计算误差并表现出明显的边界效应。 hp -PD 的结果与解析解完全一致，不仅说明其能精确施加固定边界条件，而且再次展现了其高精度。

图6 两端拉伸算例不同影响域的应变计算精度比较

图7 一端固定一端拉伸杆

图8 一端固定一端拉伸杆应变分布比较

5 结 论

本文分别通过修正微模量和建立边界虚拟键有效改善了一维键型PD方法的积分误差和边界效应，建立了高精度PD方法 hp -PD ，显著提升了PD的计算精度，准静态常应变问题能达到机器精度。应强调的是，本文发展的 hp -PD 方法不破坏PD方法原有的优点，不引入待定的计算参数，几乎不增加额外的计算量，无需采用繁琐的体积修正，也不引入需额外处理的虚拟粒子，实现起来简单方便，值得进一步向二维和三维问题拓展。