无网格法求解一类分段连续型延迟偏微分方程

钟 霖， 马淑芳， 莱 蒙

(东北林业大学 理学院，哈尔滨 150040)

1 引 言

Myshkis[1]最先发现存在分段连续型的延迟微分方程，Wiener等[2,3]对该类方程解的性质进行了研究。该类方程同时具有微分方程和差分方程的性质，能更精确地描述反馈控制和混沌系统等领域的一些问题，因此受到学者的高度重视。延迟微分方程的解析解不易获得，因此，发展该类方程的数值解研究十分必要。目前，对于该类方程数值解的稳定性、振动性和周期性已有大量研究。文献[4]研究了生态学中自变量分段连续型延迟Logistictic方程的数值解稳定性。文献[5]讨论了非线性分段连续型延迟偏微分方程数值解的渐近稳定性，给出了non-confluent Runge -kutta方法针对标量方程的稳定充要条件。文献[6]运用θ-方法和单腿θ-方法讨论了分段连续型延迟微分方程数值解的稳定性。

近年来，分段连续型延迟偏微分方程也引起了广泛的关注。文献[7]运用Galerkin法研究了分段连续型延迟偏微分方程，证明了在解析解渐近稳定的条件下，半离散和全离散方法的数值解都是渐近稳定的。文献[8]利用θ-方法研究了超前滞后型分段连续型偏微分方程,得到了数值解渐近稳定的条件。

本文考虑如下分段连续型偏微分方程：

(1)

式中t>0,a,b∈R,u(x,t):Ω=[0,1]×[0,∞)→R，v:[0,1]→R，[·]表示最大取整函数。方程(1)为对流-扩散方程，是一类基本的运动方程。该类方程可以描述在以速度为b运动的河流中污染物浓度u(x,t)的变化,其中a2ux x为扩散项，bux x(x,[t])为离散时间的对流项[11]。文献[9]采用θ-格式求解方程(1),给出了格式依赖于网格比的稳定性条件。当θ=1/2(Crank-Nicolson格式)，网格比是500时，方法是不稳定的。这与经典的Crank-Nicolson 格式具有无条件稳定性不一致。为了克服网格比对数值方法稳定性的影响，本文考虑采用无网格法求解方程(1)。无网格法是建立差分格式时，不需利用预定义的网格信息进行离散的方法[10]，可方便地模拟复杂形状的流场，并在处理网格移动和畸变等问题时有明显的优势。

本文主要目的是利用无网格法求解方程(1)，并分析方法的稳定条件，最终得到不依赖于网格比的稳定性条件。

2 分段连续型延迟偏微分方程的求解

为得到该方程的离散格式，令时间方向的步长为Δt=1/m，m为正整数。时间节点tn=nΔt(n=0,1,…)。

利用θ-加权有限差分(0≤θ≤1)离散方程(1)有

θ[a2ux x(x,t)+bux x[t]]n + 1

(2)

式中un=u(x,tn)。整理有

un + 1=un+(1-θ)Δt[a2ux x(x,tn)+bux x(x,[tn])]+

θΔt[a2ux x(x,tn + 1)+bux x(x,[tn + 1])]

(3)

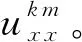
(4)

即

(5)

在区间[0,1]上选择节点xi(i=1,…,N)。i=2,…,N-1时为内点，x1和xN为边界点。利用径向基函数的组合近似u(x,tn)有

(6)

表1 典型的径向基函数

将式(6)代入式(5)并配置每个节点xi(i=2,…,N-1)有

(7)

将以上方程进行简单的处理有

(8)

通过在边界点x1和xN处使用边界条件可得

(9)

(10)

从而，由式(8～10)联立可得

(A-θΔta2B)Λk m + l + 1=[C+(1-θ)Δta2B)Λk m + l+

ΔtbBΛk m

(11)

其中

整理可得

DΛk m + l + 1=EΛk m + l+FΛk m

(12)

3 稳定性分析

(13)

化简可得

(l=0,1,2,…,m-1)(14)

(15)

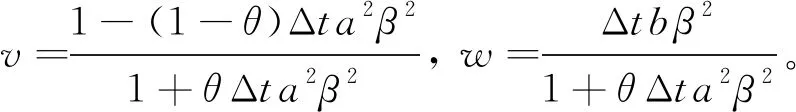
递归可得

(16)

整理有

(17)

定理1若|b|≤a2成立。当满足如下条件时，即

当m为偶数时

(18)

(19)

方程(11)是稳定的。

推论1当θ=1时,该方法是无条件渐近稳定的。

注1 式(18,19)中β是傅里叶分析的波数，其计算公式是β=2π/波长。适当的波长可导致式(18,19)的Δt的上界很大，而通常Δt取值很小，故β对于Δt的取值无太大影响。

4 数值算例

为验证所得结果，首先给出两个范数，

(20)

(21)

算例1[9]考虑方程(22),

(22)

由于本文要研究网格比r=Δt/Δx2=500，θ=1/2时的稳定性，故取时间步长为Δt=1/500，取Δx=1/500对应到文献[9]的网格比为500。由文献[16]可知，方程(1)在t为整数时的精确解为[e-a2π2+b(e-a2π2-1)/a2]tsin πx。表2给出了在t=1时，不同c值下，数值解与精确解的误差，由表可知总体趋势是c越小误差越小，故以下均取c=Δx2。方程(22)的精确解与数值解误差列入表3，可以看出，该数值方法具有较高精度。

表2 不同参数c下精确解与数值解的误差

图1利用Matlab模拟该方法在t∈[0,10]，Δt=1/500，Δx=1/500，θ=1/2，c=Δx2时的数值解。可以看出数值解是渐近稳定的。因此解决了文献[9]网格比为500不稳定的现象，证明了该方法的适用性。

算例2[9]考虑方程(23)，

(23)

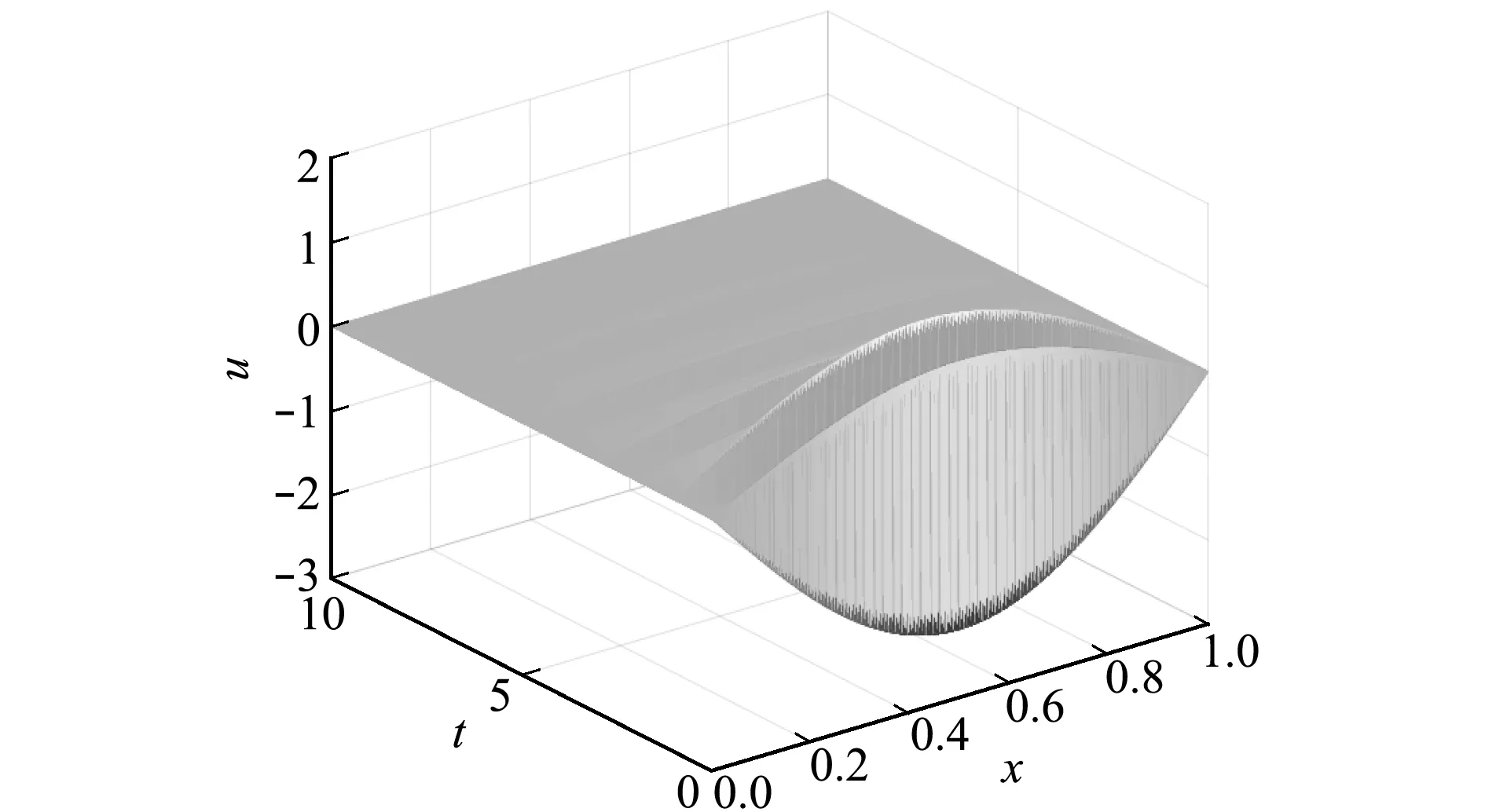
图1 方程(22)的数值解

图2和图3为在t∈[0,10]，Δt=1/3000，Δx=1/10，θ=0和0.25时方程(23)的数值解；图4和图5为t∈[0,10]，Δt=1/100，Δx=1/40，θ=0.75和1时方程(23)的数值解。可以看出，数值解是渐近稳定的,从而验证了定理1所得的结论。

由于径向基函数便于向高维问题推广，故考虑n维分段连续型偏微分方程：

(24)

式中U(x,t)∈Rn,V(x)∈R,C0∈Rn,t>0,L,M∈Rn × n。

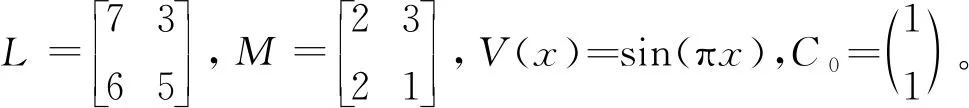
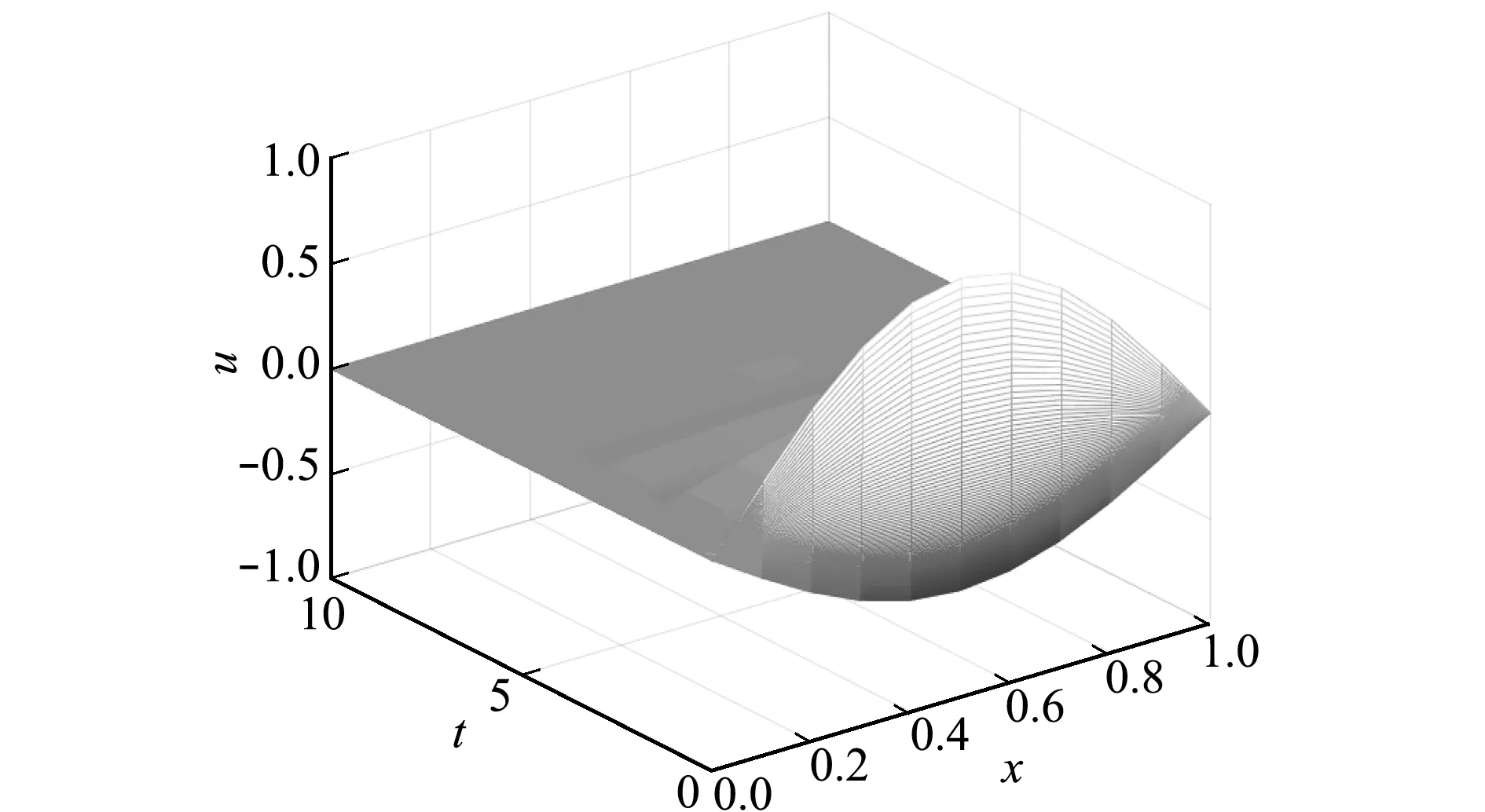
图2 方程(23)θ=0时数值解

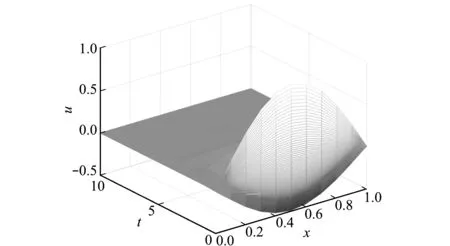
图3 方程(23)θ=0.25时数值解

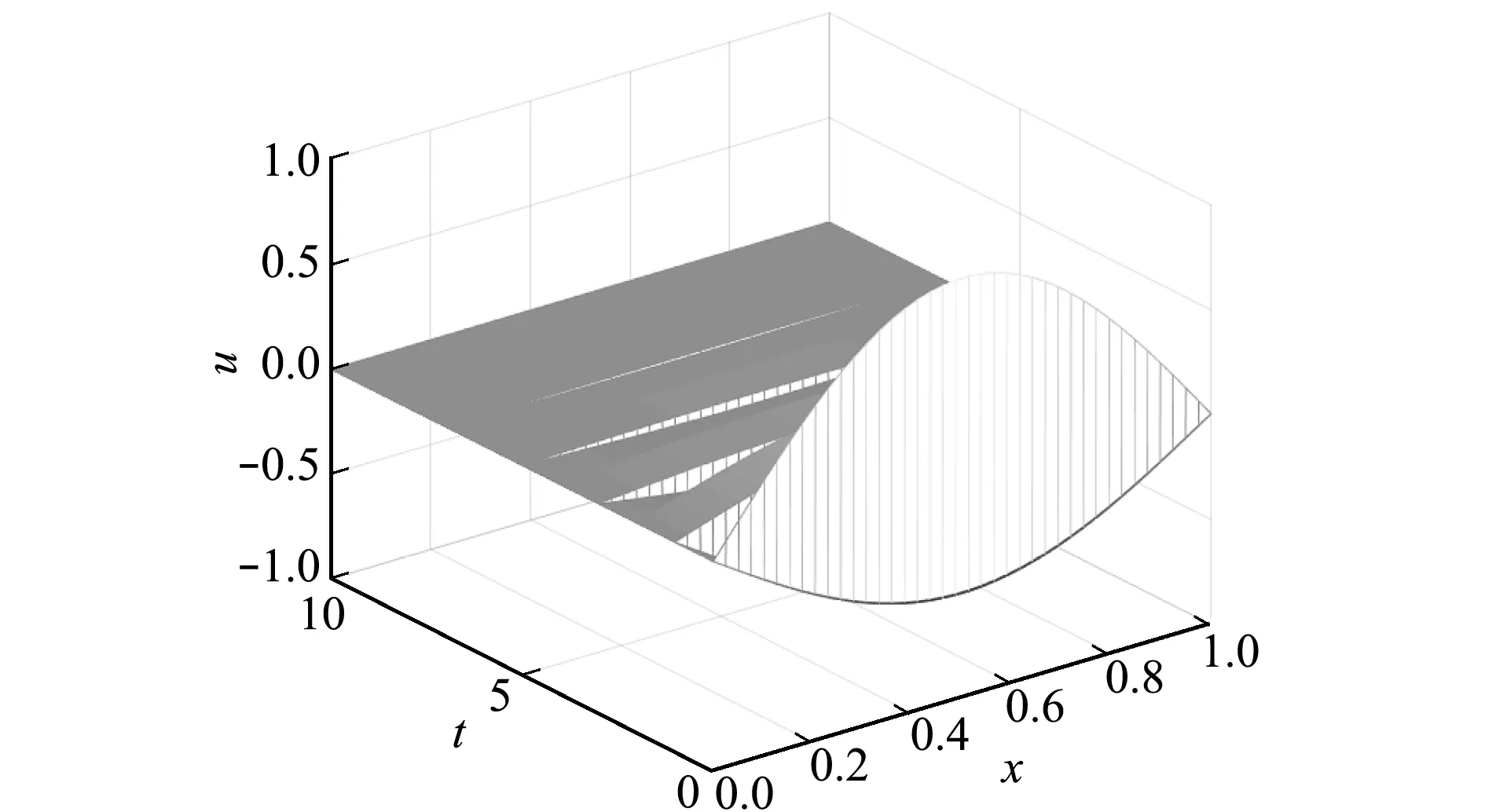
图4方程(23)θ=0.75时数值解

Fig.4 Numerical solution forθ=0.75 in Eq.(23)

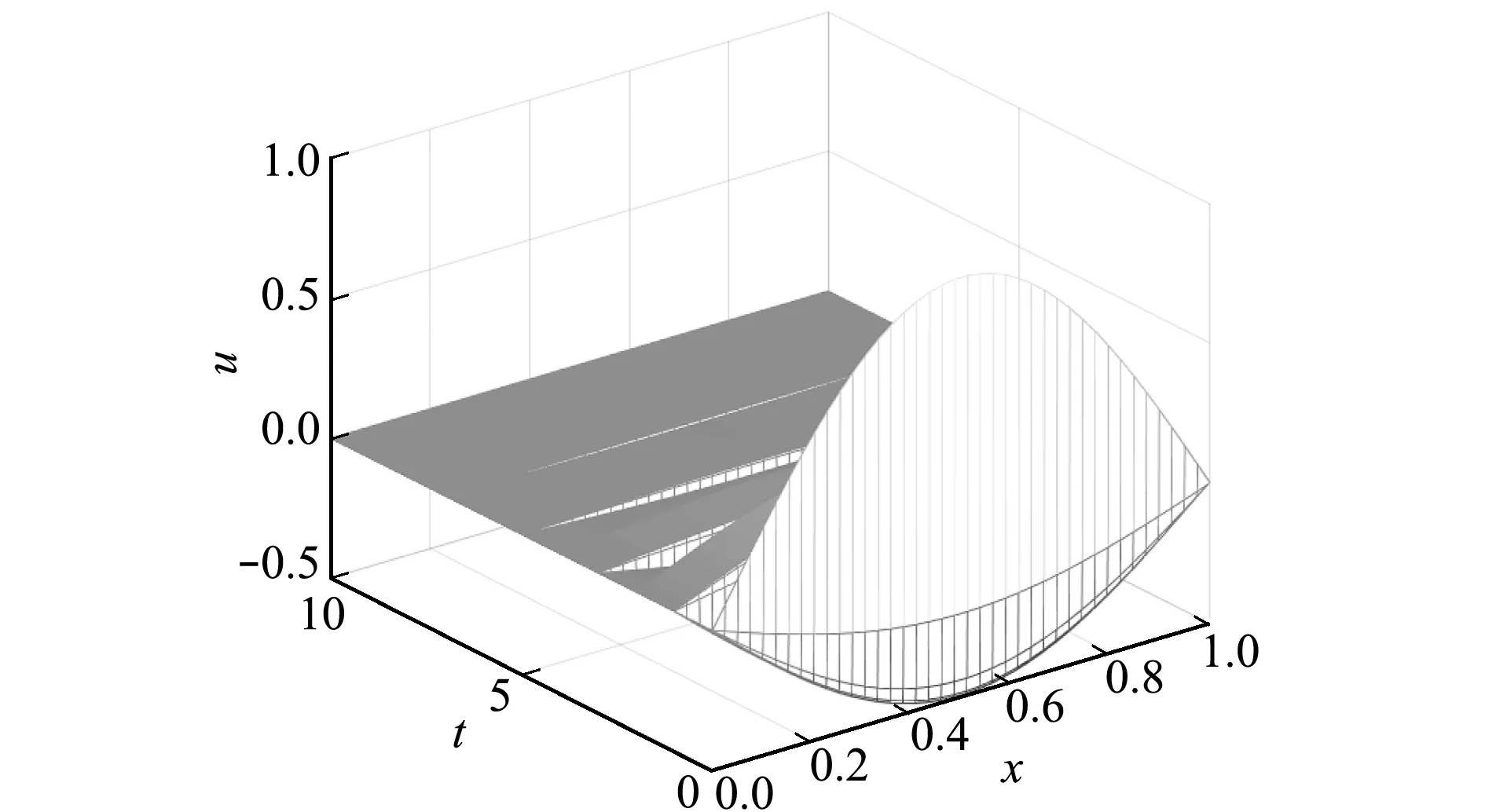
图5 方程(23)θ=1时数值解

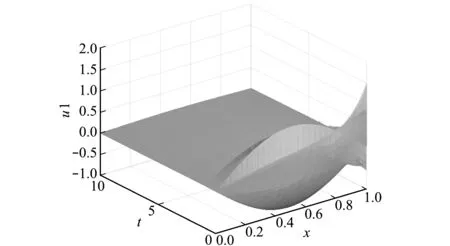
图6 数值解分量图u 1

图7 数值解分量图u 2

5 结 论

本文采用了MQ径向基函数的无网格法求解了分段连续型延迟偏微分方程，使用了θ-加权有限差分法，然后利用径向基函数的组合来近似求解方程，并利用配点法得到了计算数值解的方程组，最后给出了该方程的稳定性分析。数值算例验证了方法的有效性和稳定性，进一步表明所采用的数值方法可以有效推广到n维分段连续型偏微分方程。