基于改进磁链函数的无刷直流电机低速换相策略研究*

许 安, 文家燕,, 罗文广

1.广西科技大学 电气与信息工程学院，广西 柳州 545006；2.广西科技大学 广西汽车零部件与整车技术重点实验室，广西 柳州 545006)

0 引 言

无刷直流电机(BLDCM)因为其结构简单、功率密度高、易于控制而广泛应用于各个行业，且其无位置传感器控制使电机可以应用于高温、有强腐蚀气体等恶劣工况中。因此,BLDCM的无位置传感器控制备受研究人员关注。

文献[1-5]分别使用了反电动势过零法、反电动势积分法、状态观测器法、磁链估计法及高频脉冲注入检测法对转子的位置进行估计。前4种方法受电机转速的限制，低速时效果不佳；高频注入检测法仅适用于凸极电机，应用范围受限。文献[6]构建了一个与转速无关的函数，该函数称为磁链函数，通过设定一个阈值并与函数值进行比较，得出电机换相时刻。理论上该函数与速度无关，但实际上函数值会受到噪声的影响产生数值波动，尤其是在电机低速运行时。文献[7]通过一种离线标定的补偿方式减小换相误差，但误差是随机的，因此该方法在实际应用中的可靠性还需考量。文献[8]通过滑动平均滤波器来抑制噪声，但是考虑到增加窗口长度会造成严重的相位滞后，因此噪声抑制效果并不明显。文献[9]提出了一种带积分结构的磁链函数，通过对线反电动势积分，消除原磁链函数中的微分项，在一定程度上抑制了噪声，同时采用一阶低通滤波器(LPF)抑制初值误差与零漂，取得了不错的效果，但是一阶LPF只能抑制零漂，不能消除，并且该方法还需要进行相位补偿和额外的延时处理，造成了更多的计算和一定的换相误差。文献[10]取消了磁链函数中的微分项，简化了计算，在稳态时具有不错的效果，但是当电机受到干扰时会有误换相的可能。文献[11]使用一种自适应补偿的手段，提高电机高速运行时换相的准确性。文献[12]对磁链函数低速时的可靠性及高速时的精确性进行了分析与改进，虽然结果良好，但软硬件较复杂，限制了磁链函数的应用范围。

从结构上看，磁链函数非常适合用于BLDCM的低速换相策略，但函数的数值波动严重削弱了其可靠性。为此，本文在文献[9]的基础上采用带通滤波器(BPF)消除偏置误差，避免延时；同时引入一种新型换相判断机制，抑制数值波动带来的影响，保证了换相的可靠性。

1 磁链函数误差分析

1.1 磁链函数的构造和换相原理

通过文献[6]可得磁链函数(以下简称G函数)的表达式如下：

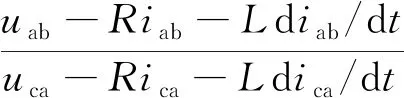
(1)

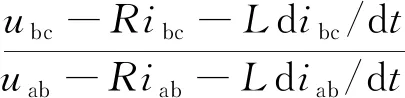
(2)

(3)

式中：hab、hbc、hca为线线反电动势；uab、ubc、uca为线电压；iab、ibc、ica为相电流之差；fab、fbc、fca为线线反电动势函数；R为相电阻；L为相电感；ke为反电动势常数；ω为转子角速度；θ为电角度。

理想的磁链函数波形如图1所示。在换相点(CP)附近函数值从正无穷跳变为负无穷，具有类似反比函数的特性，因此可以利用这一特性进行换相点检测。传统的做法是设定一个阈值，然后与G函数的绝对值进行比较，当某个时刻的函数绝对值大于阈值时即为换相时刻。理论上G函数与转速无关，再此该方法可以适用于整个转速范围。

图1 理想磁链函数与换相信号波形

1.2 磁链函数的误差分析

理想的G函数可以准确表示出换相点附近的特征，但若考虑实际工况的约束，函数会因电流、电压噪声产生巨大的数值波动，影响换相点的判断，导致换相提前甚至误换相，严重削弱了系统的鲁棒性。由文献[7]可知，G函数主要受电流噪声的影响，故本文重点讨论转速、电流噪声与G函数的关系。

以Gbc_ab(θ)为例，根据式(2)可得G函数的误差表达式：

(4)

其中，dhbc和dhab分别由式(5)、式(6)得到：

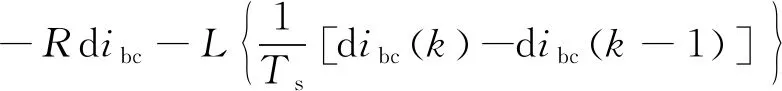
(5)

(6)

式中：Ts为采样周期。

为了使分析更贴合实际，需得到一个真实电流噪声的分布。本文通过试验测得电机相电流的波形，如图2所示。

图2 相电流示波器采样波形

通过MATLAB工具箱，计算出电流的均方根误差σ=0.005 6 A，结合该均方根误差和式(4)～式(6)，得到G函数在换相点附近的3σ误差分布图，如图3所示。其中：R=1 Ω，L=0.3 mH，Ts=0.2 ms，ke=3.39 mV·r-1·min。

图3 G函数误差分布

由上述讨论可知，虽然电流噪声很小，但G函数仍会在换相点附近产生巨大的误差，并且随着电机转速的降低，误差会进一步增大。可以从以下3个方面说明该问题。

(2)G函数中含有微分项，会引入额外误差，并且该误差受采样频率的影响，采样频率越高所带来的数值波动越大;

(3) 当θ趋近换相点时，有fab→0，导致式(4)中2项系数趋于无穷大，并且该特性会强化第1点的影响，造成数值的巨大波动。

其中，第3点是G函数固有的性质；第1点和第2点是导致G函数数值波动的主要原因，单纯通过抑制噪声来减小磁链函数的误差是不够的。因为再小的噪声仍会被放至很大，所以需要从函数的结构上对其改进。

2 换相策略的改进

2.1 带积分结构的磁链函数

从上述分析结果可得，因噪声的存在，磁链函数的准确性与转速息息相关，限制了G函数在低速场合中的使用。因此，为了减小噪声对G函数的影响，文献[9]提出了一种带积分结构的磁链函数(以下简称F函数)，具体表达式如下：

(7)

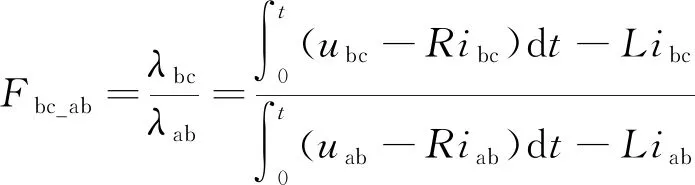
(8)

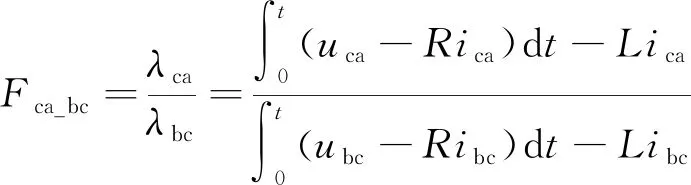
(9)

式中：λab、λbc、λca为电机线转子磁链，即λab=λa-λb，λbc=λb-λc，λca=λc-λa。

因为转子磁链是一个正负交替变化的周期函数，所以必然存在零点，这意味着F函数也存在跳变的过程，如图4所示。从图4可以看出，磁链波形过零点时刻，就是F函数的跳变时刻。与G函数判断不同的是，F函数的换相时刻需要在检测出跳变点后，延时30°电角度，这是因为F函数对线反电动势进行了积分。积分虽然改变了相位，但消除了微分项，从结构上避免了函数对噪声的放大，使F函数更加平滑。与G函数相比，F函数具有更小的数值波动，可以获得更准确可靠的换相点。

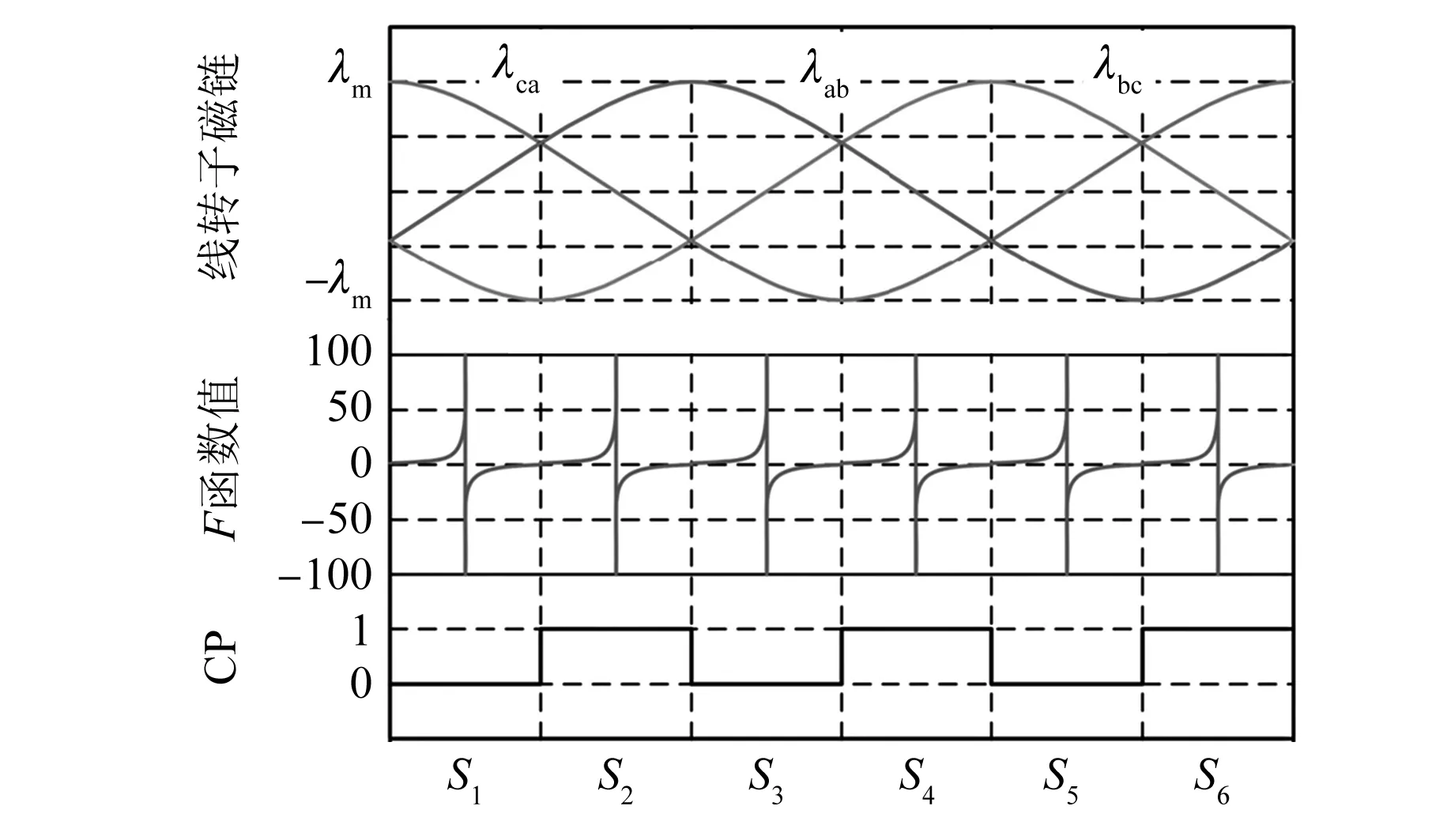
图4 线转子磁链函数、F函数及换相信号

2.2 纯积分模型的优化

从式(7)～式(9)可知，F函数存在积分结构，故必然存在零漂和初值误差的问题。为了消除其带来的不利影响，需要对纯积分模型进行优化。结合文献[13-15]的内容，本文采用BPF代替理想积分器，具体表达式如下：

(10)

式中：μ、ωn为滤波器参数。

图5 BPF Bode图

图5为BPF的Bode图。由图5可知，通过对ωn的选取可以得到BPF的中心频率，通过μ的选取可以得到不同带宽和相位特性。若选择ωs=ωc(其中ωs为电机电角度频率，ωc为BPF中心频率)则有零相位改变，即λab与fab同相位，此时无需30°电角度延时，一定程度上减小了换相误差；若增加μ，可以得到更大的带宽以及更平缓的相位变化，减小μ则有更窄的带宽、更剧烈的相位变化。值得一提的是，虽然采用BPF会使磁链波形产生畸变，但是该策略有效实施只需要磁链过零点的信息。本文中，采用实时调节BPF中心频率的策略，使ωs与ωc相等，得到一个零相位滞后的磁链过零点时刻，无需额外的相位补偿即可保证相位的精度。

2.3 换相点判断

低速时G函数受噪声的影响，产生巨大的数值波动，而传统换相点判断方法是将G函数的绝对值与阈值进行比较，得出换相时刻。相比较而言，F函数对噪声不敏感，波形相对平滑，如文献[9]所示，可采用符号的改变作为换相点判断的依据，提高换相点判断的准确性。然而前者会因为数值波动造成换相的提前或者误判，后者会受到微小数值波动的影响，存在误判的可能。因此，为了提高判断的可靠性，本文提出了一种新的判断机制，即采用一个新变量X替换对F函数或G函数数值的直接判断，同时动态调节阈值，紧跟电机运行状态，避免误换相的发生。X的定义为

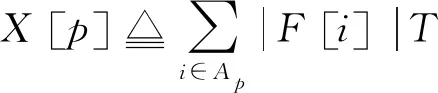
(11)

阈值TH的动态调节

式中:T为采样周期；Ap为第p个导通周期内全部采样时刻的集合；N为一个大于1的正整数；F为Fab_ca、Fbc_ab、Fca_bc三者之一，根据不同的扇区选取不同的磁链函数，选择的顺序可参考表1，同时|F[i]|≤U,U为一个合适的正数；α、β为权重系数。

表1 F函数与扇区

换相点的判断方法为,在第p个导通周期内，判断X[p]是否大于TH[p]。如果为真，则进行换相;如果为假，则继续保持原状态。

变量X的本质是对F函数的积分，积分的存在进一步抑制了F函数的数值波动，大大降低了误换相的可能。虽然在理论上一个换相周期内F函数对电角度的积分是不存在的，但是由X[p]的定义可知，对F函数限幅后，在理论上，X[p]在转速不变的情况下是一个定值，因此可通过判断X[p]的大小得出换相点位置。通过式(12)，使得阈值TH能够在不同速度下自动匹配到一个合适的值，防止误换相的发生。

3 仿真试验

表2 BLDCM参数

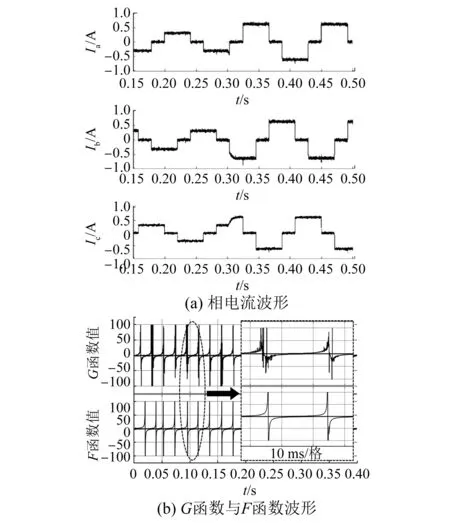
图6 G函数与F函数对比结果

图6(a)为施加噪声的相电流波形，图6(b)为G函数与F函数的波形。可以看出，在电流噪声的干扰下，G函数的数值呈现出巨大的波动，这与误差分析的结果一致。而F函数的波形相对平滑，说明F函数可以抑制噪声的影响，拥有更准确的换相信息。

图7(a)为基于LPF的定子磁链波形，图7(b)为基于BPF的定子磁链波形。可以看出，前者不能消除初始磁链误差，因此各相定子存在一个直流偏置并且无法消除，这会导致磁链过零点的提前或者滞后，从而造成换相误差。而BPF可以消除由初始误差造成的直流偏置，减小直流偏置对磁链过零点时刻的影响，从而提高换相精度。

然后验证基于BPF的F函数换相策略的效果。Simulink仿真框图如图8所示。在不同的转速和负载下，将霍尔信号与由F函数得到的换相信号进行对比。通过多次仿真和调节，得到α=0.53,β=0.11。

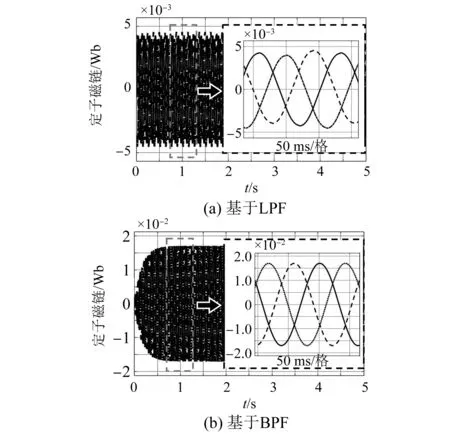
图7 磁链波形

图9为电机转速ω=60 r/min，负载从10 mN·m(电机额定负载的10%)变为20 mN·m条件下的仿真结果。图9(a)为相电流波形，图9(b)是F函数、F函数CP和霍尔CP波形，图9(c)是电机转速与负载波形。从图9(b)可以看出，通过实时调节BPF的中心频率，能够获得一个准确的换相时间点并且无需30°电角度的延时，而且函数CP信号与霍尔CP信号几乎趋于一致。当负载从10%跳转至20%时，换相时间并未受到明显影响，仍具有较高的准确性，说明该策略在低速时可以很好地抑制噪声，并且能够在一定的扰动下获得精确的换相点。

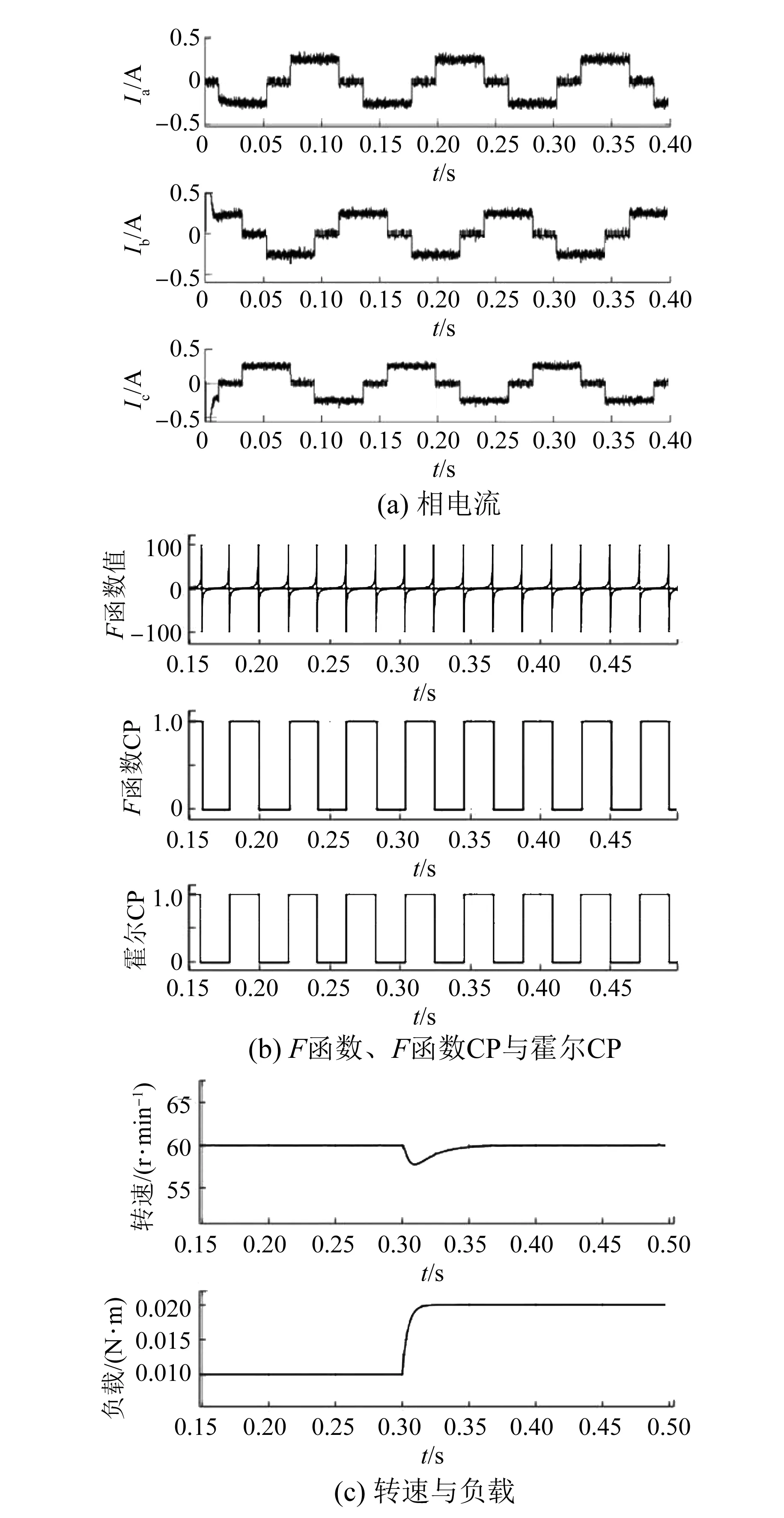
图9 60 r/min仿真结果

图10为电机转速ω=120 r/min，负载从40%变为80%条件下的仿真结果。从图10可以看出，稳态时，系统能够准确识别出换相位置，同时，当电机受到较大的负载波动时，F函数CP与霍尔CP有一个较小的位置误差，但是仍可以保证电机的稳定运行，说明该策略拥有较强的抗干扰能力。

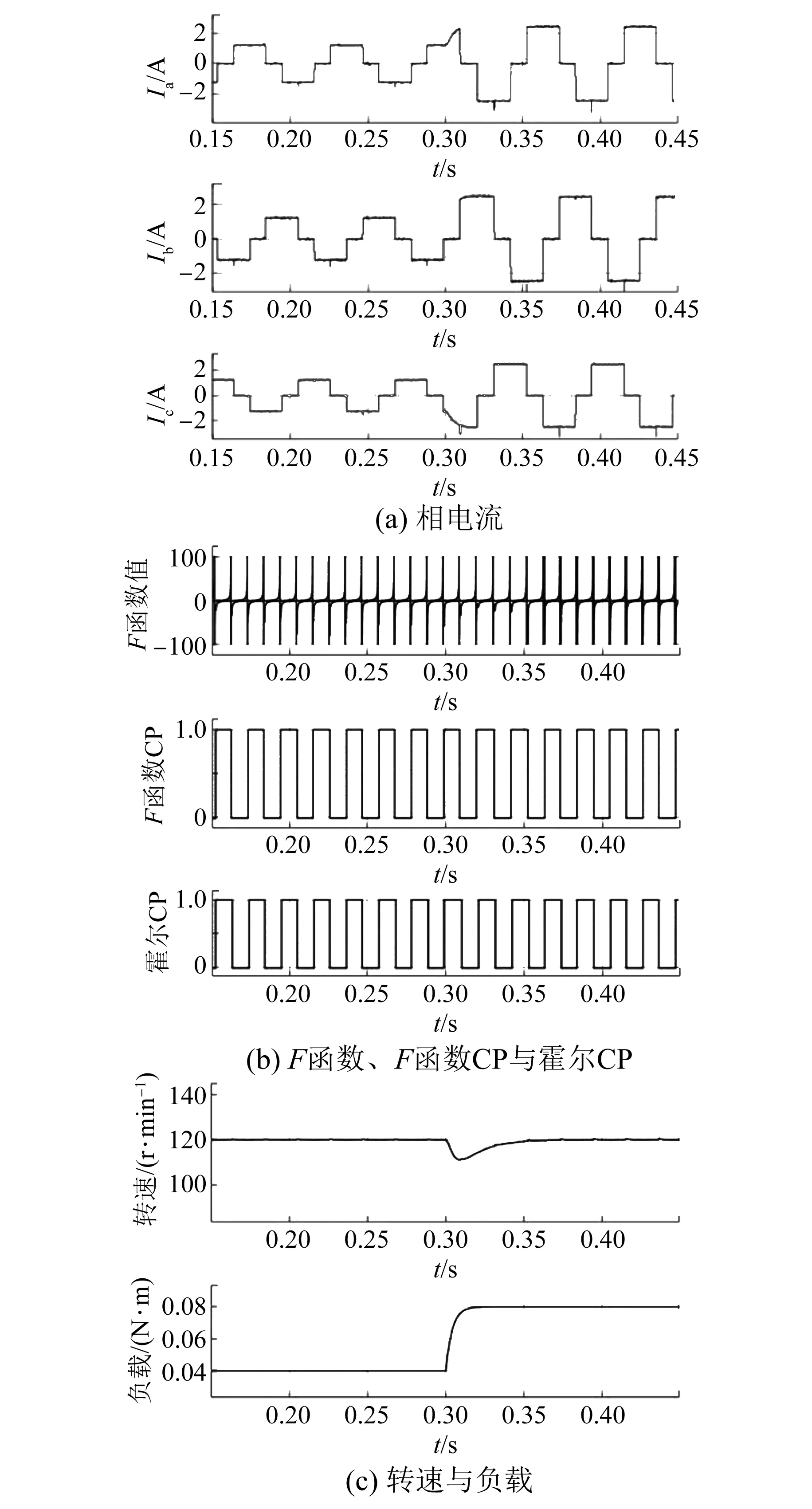
图10 120 r/min仿真结果

图11为电机转速120 r·min，80%负载下，F函数与换相信号的局部放大图。不可避免地，在某些情况下，F函数在换相点附近仍存在数值波动，若采用符号跳变的判断机制存在误换相的可能，但是从图11可以看出，本文中的判断机制可以准确识别出换相时间点，说明该机制拥有良好的可靠性。

图11 F函数、F函数CP与霍尔CP的局部放大

4 结 语

(1) 针对磁链函数对电流噪声敏感问题进行深入分析。结合分析结果，采用一种含有积分结构的新型磁链函数替代原磁链函数，以达到减小函数值波动的目的。

(2) 通过BPF替换积分器，消除了零漂和初值误差问题，同时通过调节BPF的中心频率，避免了额外的延时和相位补偿，间接减小了换相误差。

(3) 采用一种新型的换相点判断机制，通过对F函数的限幅和积分，减小数值波动的影响，同时通过对阈值的动态调节，使其能够匹配不同的电机运行状态，避免误换相。

通过MATLAB/Simulink进行仿真验证。结果表明，与G函数相比，F函数在换相点附近具有更小的数值波动，并且该换相策略可以在低速、电流噪声干扰、负载干扰的条件下，获得准确可靠的换相信号。