基于Buck电路的BLDCM调速系统设计

2021-04-30田艳兵付廷礼

电机与控制应用 2021年4期

田艳兵，付廷礼

青岛理工大学信息与控制工程学院，山东青岛 266000)

0 引言

无刷直流电机(BLDCM)转速的精确平稳控制是BLDCM面临的主要问题之一。由于电机制造和本身特点的影响，BLDCM在运行过程中存在着较大的转矩波动。同时，PID控制器具有简单、稳定的特点，在现代工业控制中占据主导地位，但是对于一些控制要求较高的对象，PID参数调节较为困难，特别是系统模型未知时，参数调节更加困难。BLDCM一般用于速度精度要求较高的场合，例如航空航天、新能源汽车等，传统的PID调速系统已经逐渐满足不了BLDCM调速系统高精度的要求[1]。针对BLDCM转矩波动明显和PID控制器参数调节困难的问题，国内外学者做了大量研究。文献[2-5]分别介绍了转矩波动产生的原因，提出对驱动电路进行改进，进而对转矩波动抑制。其中，文献[2-3]在分析转矩波动产生原因的基础上，采用Buck电路作为BLDCM控制系统的驱动，降低了BLDCM的转矩波动，但是未详细分析转矩波动减小的原因，未讨论加入Buck电路以后转速的响应和控制转速的效果。文献[4-5]分析了BLDCM转矩波动产生的原因，分别采用了SEPIC电路和Boost电路作为BLDCM的驱动电路，降低了BLDCM的转矩波动。文献[6-7]采用遗传算法(GA)与PID控制器结合的方法，使用遗传算法对PID控制器进行优化调节，结果表明，优化后的控制器对于BLDCM速度调节效果较好，超调小，转速平稳。虽然遗传算法优化后的控制器效果良好，但是采用遗传算法对PID参数进行优化的过程中，存在PID参数容易陷入局部最优的缺点。文献[8]采用模糊控制器与PID结合的方法，使用模糊控制器对PID参数进行调节，实现参数自适应控制，提高了系统的鲁棒性。文献[9]提出了内模控制与模糊控制相结合的驱动方式。在内模控制与双闭环控制相结合的基础上加入了模糊控制，改善了控制效果，但是模糊控制器的模糊控制规则目前没有较为系统的方法。

本文对BLDCM控制和驱动系统进行了设计。分析了BLDCM的运行原理和转矩波动原因，采用Buck电路直接驱动解决了转矩波动的问题。并针对传统PID调速慢、精度低以及参数调节困难等问题，采用了BP神经网络对PID进行参数调节。仿真验证表明，本文所设计的系统调节快，转速平稳，控制效果良好。

1 BLDCM数学模型

BLDCM的拓扑结构如图1所示，通过逆变桥桥臂的开通和关断进行供电驱动。方波型BLDCM采用三相六状态120°导通方式，每个时刻具有一上一下2个不同桥臂的开关导通，因此BLDCM具有6个开关状态，每一相相差120°。

图1 BLDCM的电路拓扑结构

根据基尔霍夫电压定律和电机的特点以及理想假设条件[1]可得三相绕组电压方程如下所示：

(1)

式中：ua，ub，uc分别是相电压[1]；Ra、Rb，Rc分别为相电阻；La、Lb、Lc为自感；Lab、Lac、Lba、Lbc、Lca、Lcb为互感；ia、ib、ic为相电流；ea、eb、ec为相反电动势。

根据文献[1]中提到的假设，使得：Lab=Lac=Lba=Lbc=Lca=Lcb=M，La=Lb=Lc=L。又由于理想条件下三相绕组完全对称，可得：

ia+ib+ic=0

(2)

Mia+Mib+Mic=0

(3)

将式(2)与式(3)代入式(1)可得简化后的电压方程为

(4)

定子绕组产生的电磁转矩方程为

(5)

式中：Te为电磁转矩；ω为电机机械角速度。

电机运动方程为

(6)

式中：TL为负载转矩；B为阻尼系数；J为转动惯量。

2 转矩波动原因分析

BLDCM电磁转矩波动来源主要有两部分，即传导区转矩波动和换相区转矩波动。在BLDCM运行过程中存在6个稳态区域和6个换相区域，下面就这两部分在6个换相区域内的1～2区域中进行分析，即传导区AC相导通，VT1、VT2闭合，换相区由AC相导通转变为BC相导通，VT1、VT2→VT3、VT2转变，并给出解决办法。

2.1 传导区的转矩波动抑制

AC相导通，稳态下，根据式(5)可得:

(7)

式中：Te0是稳态转矩；相电流以ia流向为正方向，且ia=-ic=I，ib=0(稳态下，B相电流为0)，I为母线电流;相反电动势以ea方向为正方向，且ea=-eb=-ec=E。

当采用传统的逆变桥，逆变器工作在PWM工作模式下时，存在母线电流测量值不准确的特点，原因是采用逆变桥工作在PWM模式下时，无论采用哪种方式，均存在单边桥臂导通状态。这里以PWM-ON型调制方式为例进行分析。上半区调制，VT1关断、VT2打开时绕组电流如图2所示。

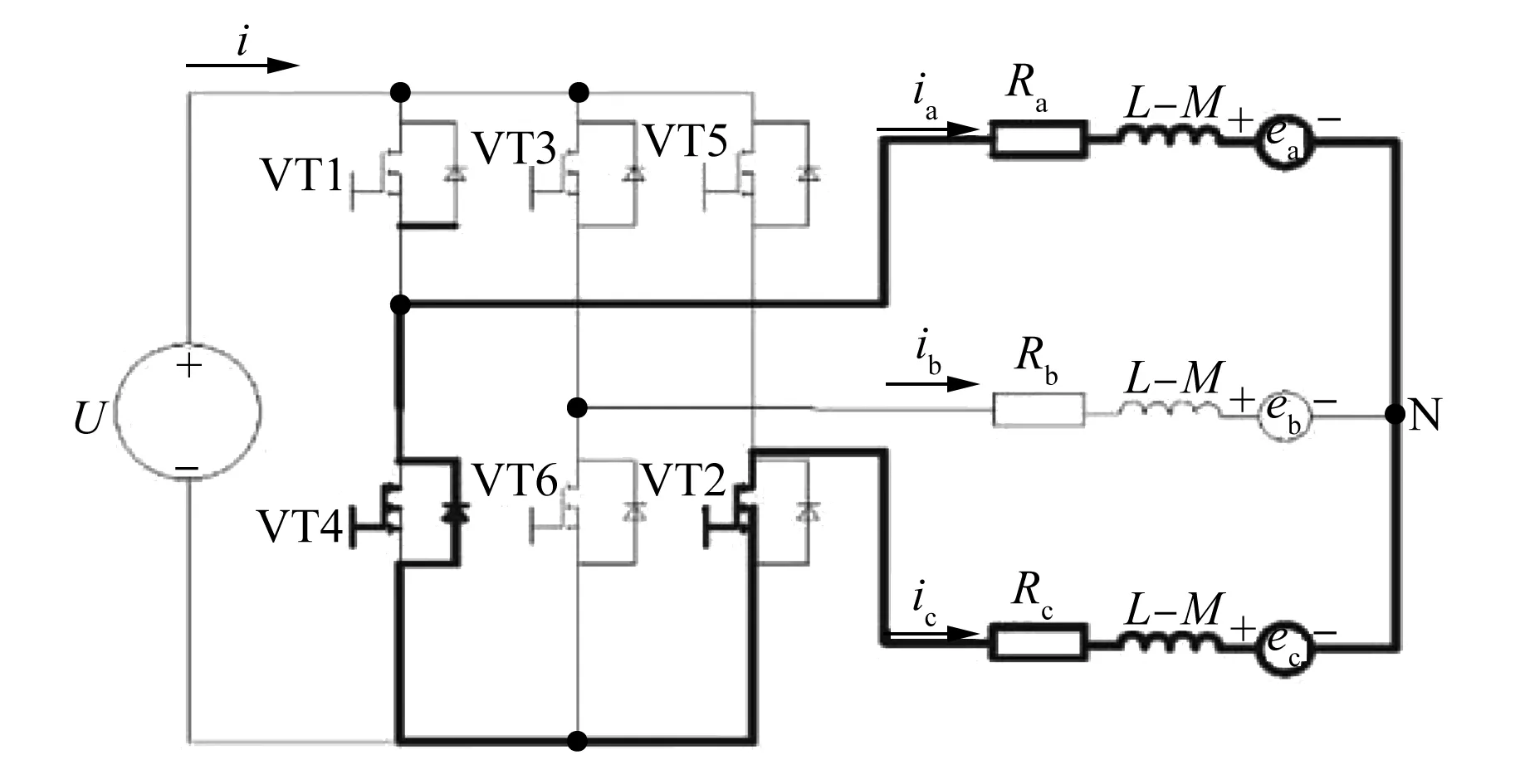
图2 导通区VT1关断VT2导通时的电流

图2中显示的电流流向是VT2→Ra→L-M→ea→N→ec→L-M→Rc→VT2(图2中标粗部分为此时电流回路)，这样会造成母线电流测量为零，无法测得电流的真实值，从而使输入控制器中的误差信号达到饱和值，控制器输出控制信号较大，反之较小，造成转矩波动。其他调制方式以及工作区域内也存在这个问题，因此易造成转矩波动。这里仅对6个稳态区域中的一个进行了分析，但是对于其他稳态区域同样适用。

2.2 换相区的转矩波动抑制

在换相区由于电机是感性负载，换相时断开相的电流不会立即停止，而是通过二极管续流，导致导通相和关断相的相电流变化速率不相等，引起转矩波动。

这里以A相断开、B相闭合、C相不变为例进行分析。

由于感性负载的存在，A相(VT1)断开后，B相(VT3)闭合前，电路拓扑结构如图2所示，虽然A相电压为零，但是由于感性负载的存在，电流不会立即变为零，由式(4)，在换相瞬间可以得到：

(8)

BLDCM中的电阻很小，可以忽略不计，又因为ia+ib+ic=0,所以有：

(9)

则由式(7)～式(9)可得：

(10)

而在换相前的稳定状态可以知道，ia和ic的稳态初值是I和-I，而ib初值是零，因此有：

(11)

由AC相导通换相至BC相导通时，以C相电流为参考方向(反方向)，根据式(5)可得：

(12)

稳态时转矩为Te0=2EI/ω。因此，转矩的波动为

(13)

而采用传统的逆变桥进行调制时，存在PWM-ON等模式，有VT1关断，VT2关断或开通，因此有：

(14)

2.3 采用Buck电路减小转矩波动原因分析

当采用Buck电路进行逆变器供电驱动时，逆变器只负责进行换相控制，对电压不进行控制，因此逆变器工作在恒通状态下，仅仅起到换相作用，而不对电压进行调制，电压由Buck根据控制器发出的控制信号进行调节，并且Buck电路选择适当的电感和电容，电压和电流不会断续，因此测量的母线电流准确。Buck电路工作原理为

U=DUin

(15)

式中:U为Buck电路输出，即为逆变桥输入；D为PWM输入占空比；Uin为电源供给Buck电路的电压。

对于传导区，由于采用了Buck电路，逆变桥工作在恒通的工作模式，避免了母线电流测量不准确引起的转矩波动。

对于换相区，同样也是因为采用了Buck电路，所以逆变桥在整个换相期间，工作在恒通状态下。因此,有：

(16)

而U=DUin，即

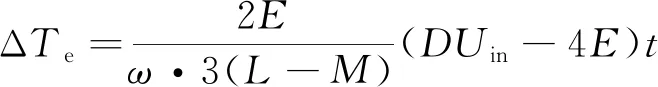
(17)

由式(14)可以得知采用Buck电路减少了在(U-4E)和(-4E)之间的切换，减小了转矩的波动，并且可以通过控制器调节占空比D大小。

当U>4E时，即电机低速工作时，换相电磁转矩脉动为正值，此时随着PWM调制波的占空比D减小，换相转矩脉动的振幅减小。

当U<4E时，即电机高速工作时，换相电磁转矩的脉动始终为负值，整个换相期间平均电磁转矩将减小，而且随着PWM调制波的占空比增大，换相转矩脉动的振幅减小。

加入Buck电路后的控制系统拓扑结构如图3所示。

图3 加入Buck电路后的拓扑结构

3 控制器的设计

虽然PID控制器具有简单、稳定的特点，在现代工业控制中占据着主导地位，但是对于一些控制要求较高和精度要求高的场合，PID参数调节较为困难，特别是系统模型未知时以及存在较大的外界非线性影响因素时，参数调节更加困难。针对PID调参困难的问题，本文采用了BP神经网络PID控制器对BLDCM控制系统进行控制。BP神经网络算法是根据最优化原理中的最速下降算法原理而产生的一种有监督学习反馈回路的控制算法，根据系统是否达到预先设定的指标而不断地进行调整。采用BP神经网络算法作为优化算法对PID参数进行调整，以使得PID 3个参数最满足调速系统要求为目标。

三层神经网络原理图如图4所示。

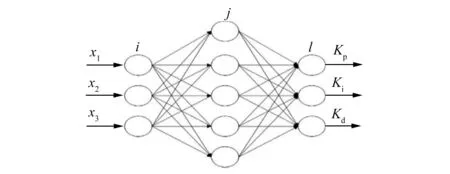
图4 神经网络原理图

神经网络计算步骤如下。

(1) 确定网络结构和各层节点数，确定初始的学习速率η、各层权系数的初值wij和vjl等。

(2) 通过采样得到输入r(k)，输出o(k)和误差e(k)=r(k)-o(k)等。

(3) 将采样得到的样本作为神经网络的输入。

(4) 通过初始的神经网络参数进行计算，并得到PID参数调节量，调节初始PID参数后计算控制量u(k)调节系统。

(5) 反向计算，调整神经网络权值，进而调节PID参数。

(6) 置k=k+1，返回步骤(2)。

本文以三层BP网络为例，详细描述BP算法。

第一层(输入层)的输入为xi(同时也是隐含层输入)，中间层(隐含层)的输出为yj(同时也是输出层输入)，第三层(输出层)的输出为zl；第一层与第二层的权值为wij，第二层与第三层的权值为vjl；tl为目标输出；f为激活函数。工作过程如下。

隐含层输出：

yi=f(∑iwijxi-θj)=f(netj)

(18)

netj=∑iwijxi-θj

(19)

式中：wij为输入层和隐含层之间的连接权系数；θj为隐含层的阈值，netj为输入层到隐含层的输出值。

输出层输出：

zl=f(∑jvjlyj-θl)=f(netl)

(20)

netl=∑jvjlyj-θl

(21)

式中：vjl为隐含层和输出层之间的连接权值；θl为输出层的阈值,netl为隐含层到输出层的输出值。

定义的误差函数为

(22)

式中：tl是输出的目标值;zl是输出层的实际值。

用误差函数推导输出节点有：

(23)

把定义的误差函数代入可得：

(24)

(25)

(26)

令δl=∑l(tl-zl)f′(netl)，可得：

(27)

同理可得:

(28)

于是权值修正值为

(29)

(30)

式中:η为神经网络的学习速率。

可得权值修改为

vjl(k+1)=vjl(k)+Δvjl

(31)

wij(k+1)=wij(k)+Δwij

(32)

从而修改神经网络权值，得到3个输出ΔKp，ΔKi，ΔKd修正由前一个控制器得出的3个参数，进而提高系统的调速性能。

4 仿真分析

在仿真平台中建立BLDCM调速系统进行仿真试验。首先对传统的逆变桥PWM-ON式调制方式和所采取的Buck方式驱动进行对比，然后在Buck电路驱动方式下对所设计的神经网络PID控制算法进行仿真。其中电机参数为：磁极对数为4，磁链为0.175 Wb，定子相电感为0.000 85 H，定子相电阻为2.875 Ω，反电动势每周期导通120°，惯性系数为0.000 8 kg·m2。

控制器如图5所示，仿真模型如图6所示。

图7～图10分别是Buck电路驱动和逆变器直接驱动方式下相电流、转矩响应、反电动势和转速响应在MATLAB/Simulink搭建的仿真模型仿真结果。

由图7可以看出，在Buck电路驱动方式下的BLDCM控制系统，相电流响应波动更小，且在施加外界转矩波动后，相电流波形更加接近梯形波。

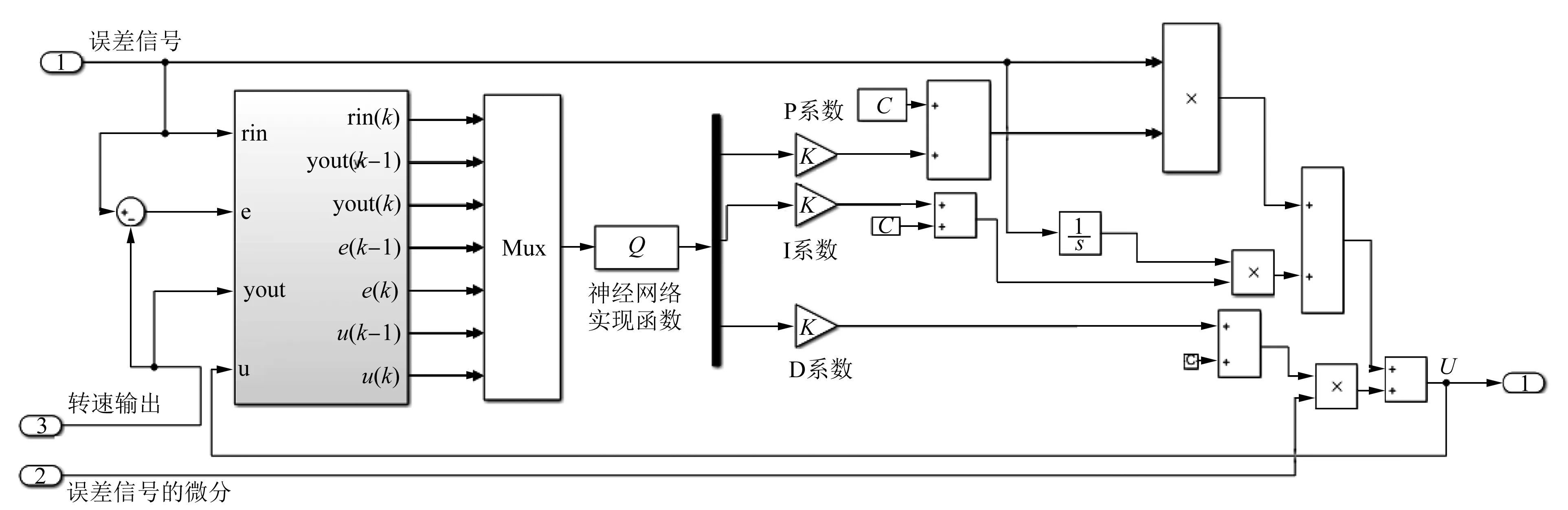
图5 控制器内部图

图6 控制系统整体图

图7 不同驱动方式下相电流对比

由图8～图10可以看出，在Buck电路驱动方式下，转矩波动更小，相反电动势更加接近梯形波，而在传统PID控制的方式下，由于加入Buck电路改善了转矩波动问题，转速也更加平稳。

图8 不同驱动方式下转矩响应对比

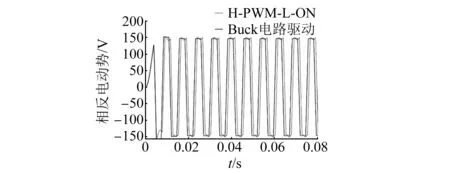
图9 不同驱动方式下相反电动势对比

图10 不同驱动下PID控制转速响应对比

由图11可以看出，采用了BP神经网络PID控制器的控制系统中，转速超调明显降低，并且在转矩变化和转速变化时，转速响应较快。采用了BP神经网络PID的调速系统仍然存在部分超调，这是由于Buck电路需要一定的时间进行电压调节电压，但是在BP神经网络PID控制器的控制下，转速初始超调和稳定后的波动明显降低，提高了系统的控制性能。