DC-DC升降压变换器协同控制器设计*

2021-04-30周志勇闫振彬

电机与控制应用 2021年4期

周志勇, 闫振彬

南京信息工程大学自动化学院,江苏南京 210044)

0 引言

随着利用太阳能、风能、潮汐能等可再生资源代替煤炭、石油、天然气等不可再生能源的日益紧迫，以及对环境的关注日益增加，开发无污染能源的需求十分迫切。因此，电力电子转换技术得到了迅速发展。其中，升降压变换器因为其电压转换范围广、输出电压可升压可降压等特点，在电动车[1-2]、燃料电池[3]、太阳能光伏[4]、智能电网[5]等实际领域中被广泛应用。然而，可再生能源是一种固有的不确定性能源[6]，容易受到气候条件等外在因素的影响。因此，需要一种控制策略提高系统的鲁棒性和稳定性。

DC-DC升降压变换器是由双线性模型描述的非线性系统[7]。为了获取恒定的输出电压，通常将非线性的DC-DC升降压变换器系统在平衡点处线性化，然后基于线性模型设计线性控制器[8]，如比例积分(PI)或比例积分微分(PID)控制器。这类控制设计思想的主要优势是设计方便、控制结构简单，成本低，是目前工业中最流行的控制方案。然而，当系统中出现负载变化时，上述控制方案不能保证系统的稳定性[9]。在此背景下，专家学者提出了一些非线性控制技术用于解决该类问题，如无源技术[10]、自适应技术[11]、自抗扰技术[12]、滑模技术[13]等控制策略。然而，上述研究仍然存在如DC-DC升降压变换器模型过于理想化，没有充分考虑系统在实际应用中存在的负载电阻扰动情况。

本文针对DC-DC升降压变换器系统中出现的负载电阻扰动问题，参考无源协同控制[14]，提出一种基于非线性扰动观测器的协同控制策略。在发生未知负载电阻扰动情况下，该协同控制策略能够有效地使系统快速恢复至平衡点，并保持稳定运行。该方法能起到有效抑制瞬态超调以及缩短调节时间的效果，实现了系统的良好鲁棒性。

1 系统模型与问题描述

DC-DC升降压变换器的平均状态模型如图1所示。假设各元器件均为理想元器件，且变换器工作在连续模式下。其中,E代表输入电压，D是占空比(控制输入)，并且u的范围属于[0,1]，L是电感，iL是电感电流，VD是二极管，C是电容，R是负载电阻，uo代表负载输出电压。

图1 升降压变换器的平均状态模型

根据二极管VD是否闭合，升降压变换器系统可分为模型Ⅰ和模型Ⅱ 2种特殊情形。

模型Ⅰ：D=1，VD关断。由图1转化的升降压变换器的模式Ⅰ如图2所示。此时，DC-DC升降压变换器的动态模型可表示为

(1)

模型Ⅱ：D=0，VD闭合。由图1转化的升降压变换器的模式Ⅱ如图3所示。此时，DC-DC升降压变换器的动态模型可表示为

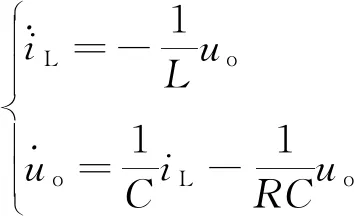
(2)

综合式(1)和式(2)， DC-DC升降压变换器的平均状态模型为

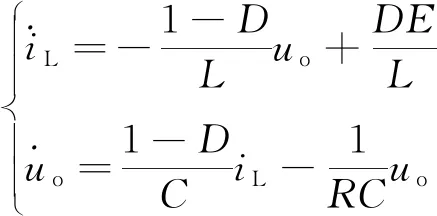
(3)

由式(1)～式(3)可知，DC-DC升降压变换器有2种工作模式：升压模式和降压模式。

图2 升降压变换器的模式Ⅰ

图3 升降压变换器的模式Ⅱ

当DC-DC升降压变换器工作在升压模式时，输出电压uo大于输入电压E，占空比D大于0.5。该模式下，电感器连接到输入电压源，在一个开关周期内持续时间更长。

当DC-DC升降压变换器工作在降压模式时，输出电压uo小于输入电压E，占空比D小于0.5。该模式下，电感器连接到负载上，在一个切换周期内持续时间更长。

2 扰动观测器设计

DC-DC升降压变换器系统运行过程中，负载电阻R是未知的时变信号，其未知及变化会影响升降压变换器系统的控制性能。考虑其影响，本文设计扰动观测器观测其值。

将系统式(3)整理为

(4)

其中：x1=iL，x2=uo。

将式(4)的第2个方程改写成：

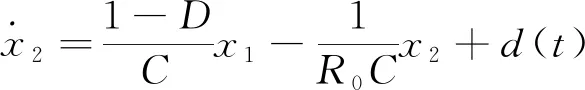
(5)

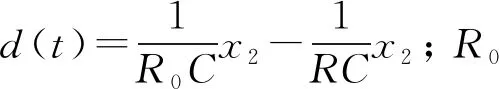
本文设计非线性扰动观测器用来估计式(5)中的负载扰动d(t)，扰动观测器形式为

(6)

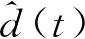
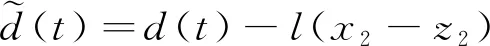
(7)

对式(7)两端关于时间t求导，可得扰动误差的导数为

(8)

从式(8)可以看出，如果假设扰动d(t)是常数，则导数为零[15]。如果扰动d(t)是以步进或缓慢斜坡的方式变化，可以理解为一种慢变，其导数是零附近很小的数。因此，根据l>0，可进一步获知扰动误差渐近收敛，即扰动误差渐近稳定。

3 控制器设计

本文提出一种基于非线性扰动观测器的协同控制方案实现对DC-DC升降压变换器系统的控制，分2步进行:(1) 通过电路稳定状态分析，得到电路稳态输入占空比和稳态电感电流，并将稳态控制输入占空比代入到稳态电感电流中得到电感电流期望值；(2) 将期望电感电流以及非线性扰动估计值代入到由协同控制算法得到的控制输入内，得到更具体的控制输入。

3.1 电路稳态分析

根据输出电压设定值uref，推导得出理想控制算法的电感电流稳定值。电感电流关系式为

(9)

(10)

电容输出电压关系式为

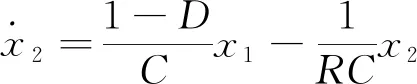
(11)

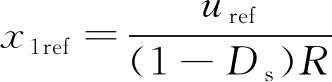
(12)

将式(10)代入式(12)，可得电感电流期望值为

(13)

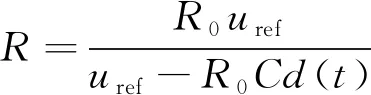
(14)

3.2 协同控制

协同控制就是采用宏变量定义系统状态变量之间的相互作用，这些宏变量规定了系统到达稳定的运动特性[16]。根据宏变量的定义，构造本文宏变量为

ψ=k(z1-x1ref)+(z2-x2ref)

(15)

其中：z1=x1；x1ref与x2ref分别为期望电感电流及期望输出电压，且为常值；k为控制系数，k>0。

系统协同控制的目的是使系统从任意初始点稳定运行到流形ψ=0，并最终沿着流形ψ=0到达期望的稳定运行点。根据协同控制思想，可选取系统状态轨迹向流形ψ=0的动态演化规律：

(16)

式中：T为系统流向流形ψ=0的收敛速度系数，T>0。

将式(4)、式(6)代入式(15)，可得协同控制律:

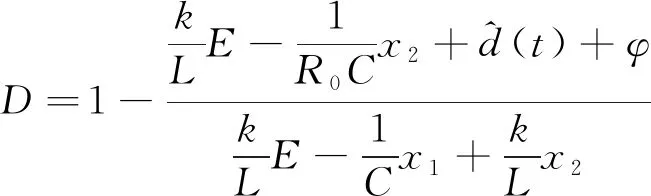
(17)

4 仿真

针对负载阶跃扰动对系统性能的影响，通过MATLAB/Simulink验证所提控制策略的可行性。在无扰动以及有扰动情况下，有效实现系统的稳定运行，保证系统的鲁棒性。整个系统的控制结构框图如图4所示。

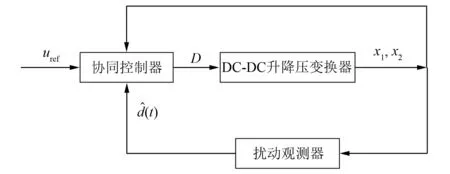
图4 DC-DC升降压变换器系统协同控制结构框图

DC-DC升降压变换器主要参数如表1所示。仿真中选取扰动观测器的观测器增益l=600。在不确定扰动影响情况下，系统的鲁棒性通过仿真进行评估。

表1 DC-DC 升降压变换器主要参数

4.1 标称升压控制器系统性能

本节给出的仿真结果代表了标称系统在DC-DC升压变换器模式下，输入电压=10 V，负载电阻R=R0=15 Ω。标称负载下的控制器系统的电感电流、输出电压、控制输入分别如图5～图7所示。

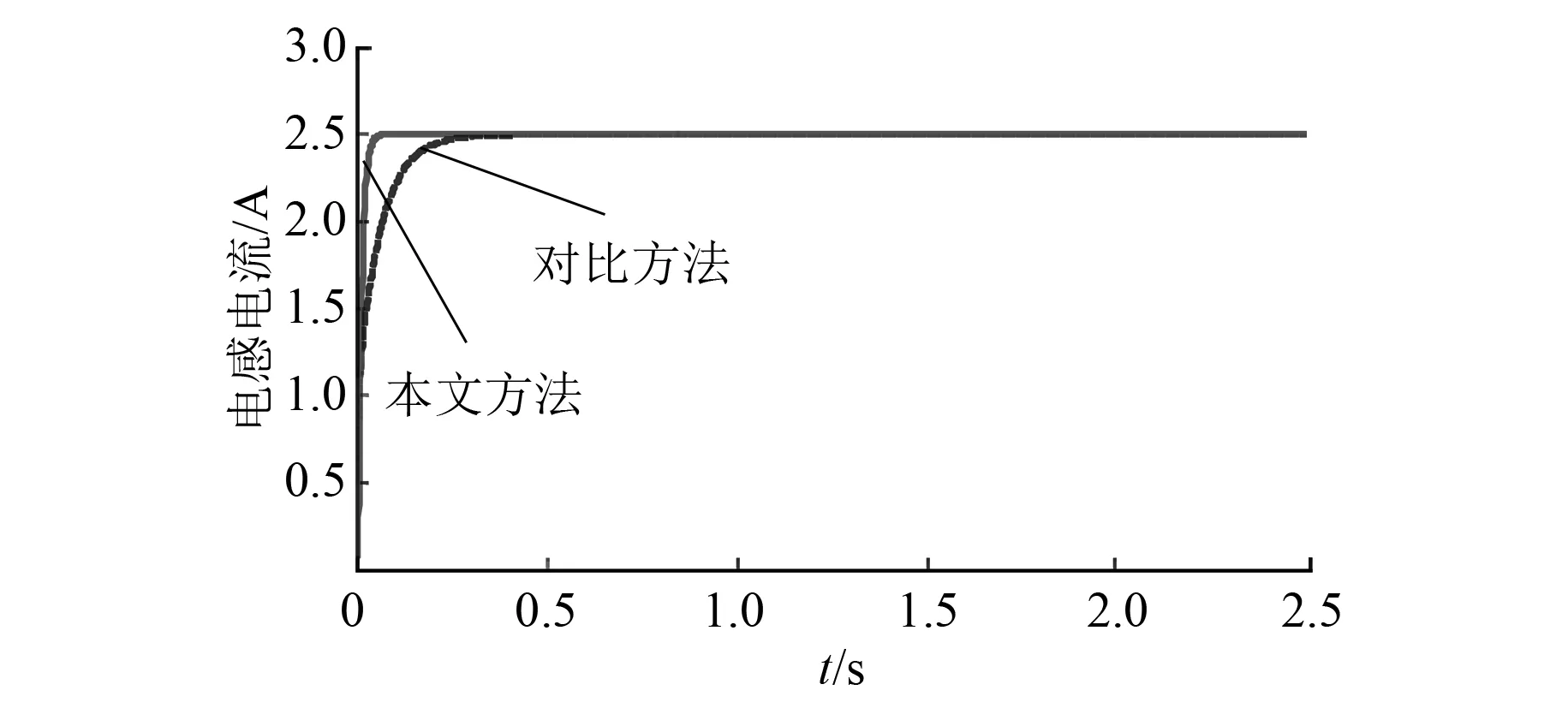
图5 标称负载下的升压控制器系统的电感电流

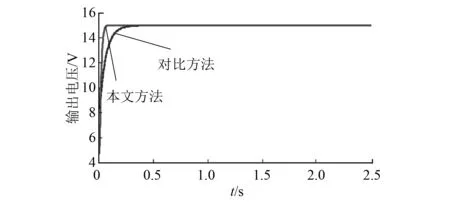
图6 标称负载下的升压控制器系统的输出电压

图7 标称负载下的升压控制器系统的控制输入

电感电流是由期望输出电压、输入电压以及负载电阻共同作用产生的，动态特性如图5所示；电容的输出电压在额定负载下收敛到稳态值，如图6所示；协同控制策略产生如图7所示的控制输入(占空比)。与对比方法相比，本文所提方法的电感电流调节时间从0.31 s缩短至0.06 s，输出电压的调节时间从0.34 s缩短至0.08 s，占空比的调节时间从0.21 s缩短至0.06 s。因此，这3个指标达到稳态值的调节时间均缩短。

4.2 负载扰动下的升压控制器系统性能

本节给出的结果是在DC-DC升压变换器模式下，存在负载电阻在t=1 s从15 Ω到10 Ω变化情况下的控制系统性能。

电感电流在无扰动负载的情况下，本文所提方法收敛到稳定状态的调节时间比对比方法要短。在t=1 s时加入负载扰动，本文方法收敛到稳定状态的调节时间缩短0.1 s，如图8所示。与对比方法相比，本文方法输出电压在刚开始很快达到期望参考值，在有负载扰动状况下，本文方法达到期望参考值的调节时间缩短0.09 s，超调上升1.33%，如图9所示。在图10中，与对比方法相比，本文方法的占空比在有负载扰动情况下，调节时间缩短0.08 s，且超调下降1.67%。

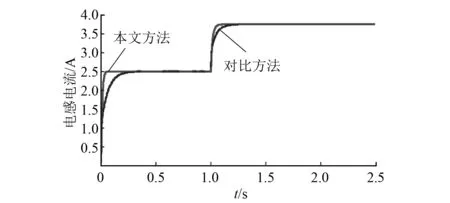
图8 负载扰动下的升压控制器系统的电感电流

图9 负载扰动下的升压控制器系统的输出电压

图10 负载扰动下的升压控制器系统的控制输入

4.3 标称降压控制器系统性能

本节给出的结果是在DC-DC降压变换器模式下，输入电压=20 V，负载R=15 Ω时的情况。如图11～图13所示，在无负载扰动情况下，本文所提的控制算法在动态性能以及稳定性能方面均比对比的控制算法效果好。由图11可知，本文方法能有效地缩短电感电流的调节时间0.32 s且过程更平稳；由图12可知，所提方法能有效地缩短收敛到期望参考电压的调节时间0.29 s；由图13可知，所提方法同样缩短了收敛到稳定状态的调节时间0.22 s。

图11 标称负载下的降压变换器系统的电感电流

图12 标称负载下的降压变换器的输出电压

图13 标称负载下的降压变换器系统的控制输入

4.4 负载扰动下的降压控制器系统性能

图14 负载扰动下的降压变换器系统的电感电流

相似地，DC-DC降压变压器存在负载电阻在t=1 s从15 Ω到10 Ω变化情况下的控制系统性能，如图14～图16所示。由图14可以看出，本文方法与对比方法相比，电感电流在面对负载扰动时恢复到期望参考值的调节时间缩短0.13 s；由图15可以看出，本文方法与对比方法相比，输出电压在面对负载扰动时恢复到期望参考值的调节时间缩短0.12 s，超调上升1.33%；从图16可以看出，与对比方法相比，本文方法在面对负载扰动时恢复到期望参考值的占空比的调节时间缩短0.07 s，同时，超调下降1.4%。