基于VPRS和DIIFPWGA算子的特色小镇融资项目模式决策

赵 辉，卜泽慧，马胜彬，陈 涛

(青岛理工大学 管理工程学院，青岛 266525)

2017年12月，国家发改委正式颁布《关于规范推进特色小镇和特色小城镇建设的若干意见》，首次提出，在乡村振兴战略背景下，目前我国正从城乡分割逐步演化到城乡一体的大格局，建设特色小镇成为推动城乡差距减少的一大推手.另一方面，特色小镇可谓是“小空间大投资”，加快特色小镇的建设有利于各地区聚集资源要素，吸引大量投资，进而使得特色小镇能够成为促进实体经济发展的新助力.因此，如何选取科学可靠的最优投资融资方案，成为推进特色小镇建设的重要抓手.

对于融资运营模式的选择，国内外学者均进行了相应的研究分析.虽然，目前关于融资运营的研究取得了一些成果，但理论上还需要进一步完善.现有的研究大都基于某种数学方法或几种方法的综合进行融资运营模式的选择，如：区间标度法[1]、两阶段完全信息动态博弈模型法[2]、效用理论[3]、投融资组合决策模型[4].但是现有研究中仍存在一些突出问题亟待解决：①动态性方面.学者们在研究融资项目时，大多忽略了时间性，导致决策动态性不足，也易使得决策结果与初衷相违背.②在研究方法方面.目前我国对于特色小镇融资运营模式的研究，定性成分太多，定量成分太少，其中部分方法由于评价指标多，没有得到精简，导致专家评审时主观性太强，从而影响评价和选择结果的客观性.③在特色小镇融资运营模式选择的指标构建、评价方法方面.其他研究领域的成熟方法在特色小镇融资运营模式评价领域应用较少.

本文建立了基于变精度粗糙集和区间直觉模糊幂加权算子的多属性决策模型，用于对特色小镇融资项目运营模式进行决策.该模型的基本思路是运用变精度粗糙集进行指标约简后，通过动态区间直觉模糊幂加权算子计算各个融资项目的综合函数值并排序，为决策者对融资项目的选择提供合理的参考.

1 变精度粗糙集基本概念

1.1 约简原理

波兰教授Pawlak提出了传统的粗糙集理论.1993年，Ziarko教授在传统粗糙集模型中引入了误差因子，从而提升了传统粗糙集处理带噪声信息系统的能力，这种允许存在一定范围内的错误分类率的粗糙集成为变精度粗糙集(VPRS).变精度粗糙集往往用于属性约简中，能够在维持原有信息系统分类信息不变的前提下，获得更加完整、精确的分类规则或决策[5].

定义1：1个信息系统由四元组S=(U,O,Vo,fo)组成.其中U是研究对象所组成的集合；对象的属性集合称为O，A称为条件属性集，D称为决策属性集，其中O=A∪D，A∩D=Ø；研究对象属性取值的集合称为Vo；fo为系统中的信息函数，为属性赋予1个信息值.

定义2：C为条件属性集合A的子集，则决策属性集D对C的近似依赖度为

λ(C,D,β)=|posr(P,D,β)|/|U|

(1)

定义3：设论域U上存在等价关系R，则U按R分类可表示为U/R={P1,P2,…,Pn}，对于X⊆U，定义X的变精度粗糙集β正区域为

(2)

其中，C(P,X)表示P关于X的错误分类率，且

(3)

定义4：当满足条件λ(C,D,β)=λ(A,D,β)，且不存在1个R⊂C，使得λ(R,D,β)=λ(C,D,β)时，此时称条件属性C是A关于D的属性约简，称关于A的属性约简的交集为A的核.若条件属性集中各Ai满足条件λ(A-{Ai},D,β)<λ(A,D,β)，则称属性A对评价指标体系结果有显著影响，应当保留，否则称属性A对评价指标体系无显著影响，约减时可将其从条件属性集中去除.

1.2 约简步骤

1) 初始化.给定β的取值范围为0≤β<0.5，S=Ø .

2) 对条件属性集中每个条件属性A，计算逼近度γ(A,D,β)和S=S∪{λ(A,D,β)}.

3) 计算条件属性集合C的核属性集合A′，当λ(C′,D,β)≠λ(C,D,β)时，取出S中的最大值λ(Ai,D,β)，并计算A′=A′∪Ai和S=S-{λ(Ai,D,β)};重复该步骤直到γ(A′,D,β)=γ(A,D,β).

4) 去除核属性集A′中对评价指标无显著影响的属性项，得到最小决策表.

2 基于区间直觉模糊幂加权几何平均算子的多属性动态决策模型

2.1 区间直觉模糊集基本理论

定义5[6]：设X为非空论域，则称X上的区间直觉模糊集D为

D={〈x,φD(x),ρD(x)〉|x∈X}

(4)

(5)

(6)

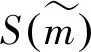
2.2 动态区间直觉模糊幂加权几何平均算子基本理论

定义8：设aj(j=1,2,…,m)∈R，则幂加权几何平均数(PWGA)算子为[7]

(7)

IIFPWGA算子的性质如下：

定理2(有界性) IIFPWGA为有界算子.若

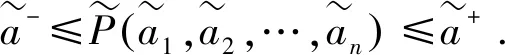
为了充分考虑时间权值对评价方案的选择影响，本文使用引入时间权值的区间直觉幂加权几何平均算子.

(8)

2.3 决策流程

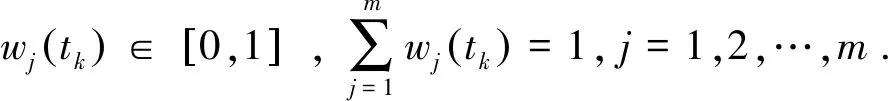
步骤1 构建区间直觉模糊决策矩阵.邀请专家以区间直觉模糊集的形式对每个评价指标在不同方案下指标影响进行评价，得到区间直觉模糊矩阵R(tk).

步骤2 对成本型指标进行规范化处理，将所有的成本型指标转化为效益型指标.

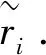
步骤6 计算各备选方案Ai的优劣排序，得到最佳方案.

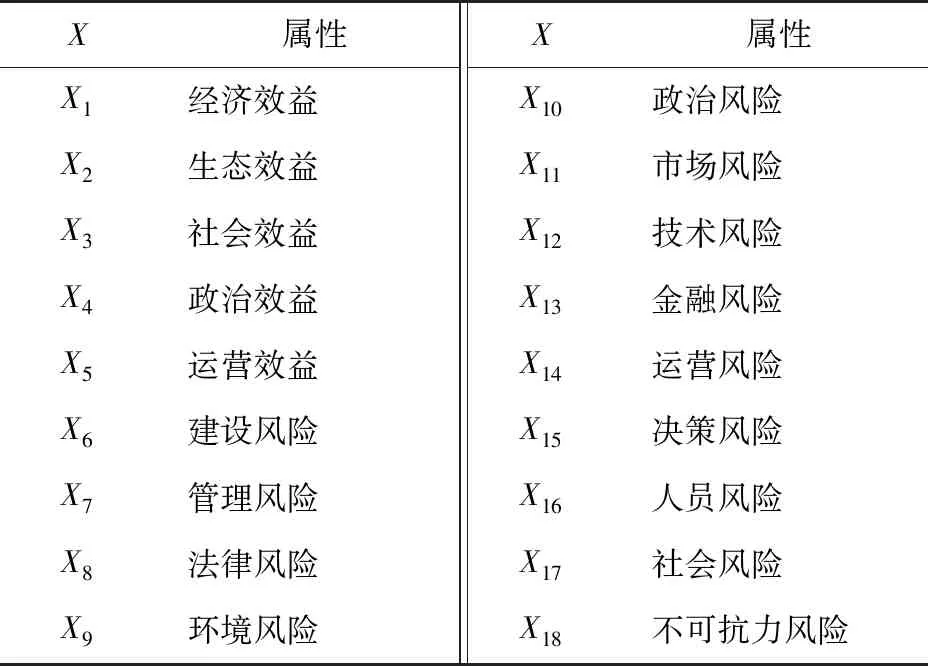
表1 初始影响指标

3 算例分析

3.1 采用变精度粗糙集对指标体系进行约简

本文以丽水古堰画乡小镇实际项目为参考，在充分调研国内外相关文献的基础上[8-9]，结合特色小镇项目目前的现状和发展趋势，根据收益与风险两大评价准则的标准，邀请相关专家初步选取18个影响指标(表1)，根据上述原理，将初步选取的影响指标作为特色小镇融资项目的条件属性集，将最大效益因素和最大风险因素作为决策属性集，运用ROSETTA软件，对条件属性集进行属性约简，从而形成特色小镇融资项目模式决策评价指标体系，如图1所示.

由图1可知，收益准则主要包含特色小镇项目所带来的经济效益、社会效益、生态效益.为保证特色小镇的绿色可持续发展，衡量经济效益是对特色小镇融资项目评价的一大要素，经济效益主要考虑到净产值率、资产负债率、营业收入、流动资金周转状况等；社会效益则应当考虑到产业贡献率、公众参与程度、公共资源的合理共享度、文化资源的开发利用等.此外，特色小镇建设过程中会对周围的环境、居民生活产生生态效益，如环境污染状况、自然资源节约利用程度、小镇植被绿化度等，因此衡量生态效益也是重中之重.

图1 特色小镇融资项目模式选择指标体系

同样，风险准则主要包括建设风险、管理风险、金融风险、法律风险、政治风险等.建设风险主要是指在进行融资项目建设时可能会受到项目延误、建设成本超出预支等不良状况影响从而导致特色小镇难以建设；管理风险主要是指在特色小镇融资项目运营中，管理层面上出现的不良决策而造成的风险，若决策严重失误时，将对融资项目造成巨大损失；金融风险主要是指当融资项目进行融资时，受到通货膨胀、利率、汇率降低等不利因素影响，进而导致难以吸引到资金；法律风险则是考虑到在融资过程中可能会存在法律不完善、法律变更等情况；政治风险则是指融资项目在进行中可能会存在着政策变动、政府担保力度下降、政府信用度降低等状况，从而影响到特色小镇项目难以融资成功.

3.2 采用区间直觉模糊幂加权几何平均算子进行方案决策

本文通过丽水古堰画乡小镇进行实例论证，经过实际考察发现丽水古堰画乡小镇进行融资时考虑采用以下5种融资方式：A1发行债券；A2资产证券化；A3PPP；A4收益信托；A5融资租赁.通过这5种方案进行特色小镇融资项目模式决策.通过属性经济效益C1、社会效益C2、生态效益C3、建设风险C4、管理风险C5、金融风险C6、法律风险C7、政治风险C8，本文对以上5种融资模式在2016—2018年丽水古堰画乡小镇融资模式进行决策分析.

步骤1 邀请相关领域投融资专家、大学教授、政府官员等6人组成专家组，根据上述8个指标对5种不同方案影响程度打分，得到各方案的区间模糊决策集.其中t1表示2016年，t2表示2017年，t3表示2018年；时间tk(k=1,2,3)权值为λ(t)=(1/6,2/6,3/6)T, 属性Gj(j=1,2,3)的权重向量为w=(0.4,0.3,0.3,0.3,0.4,0.3,0.2,0.3)T，计算结果如下：

t1时刻，各方案区间模糊决策集：

A1={〈C1,[0.71,0.93],[0.42,0.54]〉,〈C2,[0.50,0.64],[0.27,0.38]〉,〈C3,[0.74,0.83],[0.41,0.52]〉,〈C4,[0.62,0.71],[0.32,0.56]〉,

〈C5,[0.32,0.44],[0.12,0.24]〉,〈C6,[0.41,0.65],[0.17,0.26]〉,〈C7,[0.34,0.47],[0.15,0.26]〉,〈C8,[0.71,0.84],[0.34,0.45]〉}

A2={〈C1,[0.83,0.92],[0.23,0.35]〉,〈C2,[0.73,0.92],[0.15,0.26]〉,〈C3,[0.42,0.54],[0.16,0.27]〉,〈C4,[0.43,0.56],[0.23,0.36]〉,

〈C5,[0.58,0.92],[0.22,0.35]〉,〈C6,[0.34,0.56],[0.23,0.37]〉,〈C7,[0.63,0.75],[0.13,0.26]〉,〈C8,[0.64,0.76],[0.16,0.26]〉}

A3={〈C1,[0.86,0.93],[0.06,0.11]〉,〈C2,[0.52,0.66],[0.13,0.25]〉,〈C3,[0.58,0.64],[0.25,0.39]〉,〈C4,[0.87,0.96],[0.21,0.32]〉,

〈C5,[0.83,0.92],[0.15,0.27]〉,〈C6,[0.85,0.93],[0.27,0.35]〉,〈C7,[0.52,0.64],[0.16,0.25]〉,〈C8,[0.79,0.92],[0.22,0.31]〉}

A4={〈C1,[0.25,0.37],[0.11,0.25]〉,〈C2,[0.33,0.48],[0.03,0.17]〉,〈C3,[0.41,0.52],[0.22,0.32]〉,〈C4,[0.21,0.34],[0.08,0.13]〉,

〈C5,[0.13,0.24],[0.06,0.13]〉,〈C6,[0.52,0.64],[0.26,0.39]〉,〈C7,[0.43,0.56],[0.22,0.45]〉,〈C8,[0.37,0.49],[0.16,0.25]〉}

A5={〈C1,[0.71,0.82],[0.28,0.39]〉,〈C2,[0.41,0.49],[0.11,0.23]〉,〈C3,[0.61,0.75],[0.35,0.42]〉,〈C4,[0.54,0.66],[0.14,0.38]〉,

〈C5,[0.34,0.42],[0.05,0.17]〉,〈C6,[0.56,0.74],[0.34,0.46]〉,〈C7,[0.24,0.36],[0.04,0.19]〉,〈C8,[0.64,0.78],[0.32,0.48]〉}

t2时刻，各方案区间模糊决策集：

A1={〈C1,[0.73,0.87],[0.35,0.52]〉,〈C2,[0.49,0.62],[0.12,0.28]〉,〈C3,[0.51,0.65],[0.33,0.42]〉,〈C4,[0.57,0.62],[0.25,0.37]〉,

〈C5,[0.29,0.37],[0.15,0.29]〉,〈C6,[0.34,0.42],[0.15,0.27]〉,〈C7,[0.35,0.48],[0.14,0.27]〉,〈C8,[0.62,0.76],[0.24,0.47]〉}

A2={〈C1,[0.78,0.82],[0.26,0.32]〉,〈C2,[0.72,0.85],[0.17,0.24]〉,〈C3,[0.32,0.49],[0.12,0.25]〉,〈C4,[0.32,0.45],[0.13,0.25]〉,

〈C5,[0.49,0.52],[0.22,0.34]〉,〈C6,[0.43,0.59],[0.02,0.14]〉,〈C7,[0.53,0.65],[0.23,0.35]〉,〈C8,[0.63,0.75],[0.22,0.36]〉}

A3={〈C1,[0.76,0.85],[0.13,0.24]〉,〈C2,[0.65,0.71],[0.16,0.28]〉,〈C3,[0.63,0.79],[0.22,0.34]〉,〈C4,[0.72,0.85],[0.18,0.29]〉,

〈C5,[0.83,0.95],[0.12,0.25]〉,〈C6,[0.78,0.94],[0.25,0.38]〉,〈C7,[0.46,0.52],[0.12,0.25]〉,〈C8,[0.77,0.81],[0.12,0.29]〉}

A4={〈C1,[0.23,0.35],[0.12,0.28]〉,〈C2,[0.22,0.34],[0.14,0.29]〉,〈C3,[0.33,0.56],[0.37,0.48]〉,〈C4,[0.23,0.36],[0.13,0.26]〉,

〈C5,[0.12,0.26],[0.02,0.15]〉,〈C6,[0.53,0.70],[0.25,0.48]〉,〈C7,[0.42,0.58],[0.25,0.36]〉,〈C8,[0.31,0.42],[0.15,0.27]〉}

A5={〈C1,[0.63,0.74],[0.25,0.41]〉,〈C2,[0.38,0.50],[0.09,0.21]〉,〈C3,[0.59,0.75],[0.31,0.42]〉,〈C4,[0.53,0.66],[0.19,0.26]〉,

〈C5,[0.48,0.57],[0.04,0.17]〉,〈C6,[0.63,0.85],[0.28,0.47]〉,〈C7,[0.25,0.37],[0.04,0.16]〉,〈C8,[0.65,0.77],[0.38,0.46]〉}

t3时刻，各方案区间模糊决策集：

A1={〈C1,[0.61,0.74],[0.33,0.45]〉,〈C2,[0.42,0.54],[0.13,0.26]〉,〈C3,[0.52,0.76],[0.32,0.56]〉,〈C4,[0.43,0.56],[0.37,0.45]〉,

〈C5,[0.14,0.27],[0.05,0.18]〉,〈C6,[0.35,0.49],[0.13,0.20]〉,〈C7,[0.15,0.28],[0.05,0.18]〉,〈C8,[0.65,0.79],[0.36,0.49]〉}

A2={〈C1,[0.83,0.92],[0.25,0.38]〉,〈C2,[0.71,0.94],[0.14,0.27]〉,〈C3,[0.41,0.52],[0.12,0.24]〉,〈C4,[0.39,0.51],[0.23,0.35]〉,

〈C5,[0.45,0.61],[0.26,0.38]〉,〈C6,[0.31,0.45],[0.12,0.24]〉,〈C7,[0.55,0.63],[0.14,0.21]〉,〈C8,[0.58,0.67],[0.13,0.24]〉}

A3={〈C1,[0.72,0.81],[0.13,0.26]〉,〈C2,[0.69,0.77],[0.12,0.23]〉,〈C3,[0.54,0.62],[0.13,0.24]〉,〈C4,[0.64,0.71],[0.12,0.23]〉,

〈C5,[0.76,0.93],[0.23,0.37]〉,〈C6,[0.67,0.83],[0.13,0.26]〉,〈C7,[0.65,0.77],[0.15,0.28]〉,〈C8,[0.58,0.67],[0.13,0.24]〉}

A4={〈C1,[0.25,0.39],[0.18,0.29]〉,〈C2,[0.23,0.37],[0.08,0.19]〉,〈C3,[0.37,0.52],[0.26,0.34]〉,〈C4,[0.25,0.37],[0.06,0.17]〉,

〈C5,[0.17,0.25],[0.04,0.17]〉,〈C6,[0.57,0.65],[0.24,0.37]〉,〈C7,[0.47,0.55],[0.24,0.47]〉,〈C8,[0.37,0.44],[0.03,0.16]〉}

A5={〈C1,[0.56,0.73],[0.24,0.37]〉,〈C2,[0.35,0.56],[0.05,0.18]〉,〈C3,[0.69,0.88],[0.27,0.45]〉,〈C4,[0.55,0.68],[0.14,0.26]〉,

〈C5,[0.48,0.57],[0.16,0.27]〉,〈C6,[0.53,0.77],[0.35,0.47]〉,〈C7,[0.34,0.53],[0.06,0.15]〉,〈C8,[0.54,0.65],[0.32,0.46]〉}

步骤 2 对指标C4，C5，C6，C7，C8进行规范化处理.

表2 各个时刻的排序结果

表2为对备选方案在t1，t2，t3的排序结果，由于方案A2和A5对时间因素的变化较敏感，所以导致了不同时刻的排序结果大致相同，又稍有区别.由此，在进行特色小镇融资项目决策时，应当考虑时间因素对方案的影响，以使得决策更加科学合理.

4 结论

1) 本文将幂加权几何平均集结算子应用到区间直觉模糊集，以此算子进行数据集结，体现了本文的科学性.另一方面，本文通过引入动态幂加权几何平均算子，引入了时间因素来更加全面地评估整个项目，体现了本文的动态性.

2) 本文以丽水古堰画乡小镇为例，通过实例论证，证明了该方法对于特色小镇融资项目模式选择的可行性，为后续特色小镇融资项目决策提供了1种新的方法.

3) 资产证券化作为新型融资方式亦受到相关专家的推荐，评分较高.因此，结合目前我国PPP融资模式发展现状，特色小镇在实际建设运营中，可以通过资产证券化与PPP相结合的方式进行融资，进一步促进特色小镇的可持续发展.