圆钢管橡胶混凝土短柱承载力分析

刘振杰，徐培蓁，*，韩 琳，吴 瑕，王玉文，朱亚光

(1.青岛理工大学 土木工程学院，青岛 266033；2.潍坊建筑设计研究院有限责任公司，潍坊 261000；3.中国建筑一局(集团)有限公司，北京 100000)

近年来随着我国汽车行业和能源行业飞速发展，废弃橡胶逐渐增多，橡胶内部交联的网络结构，具有不溶不熔的特性[1].废弃的橡胶在自然状态下不易降解，废橡胶的回收利用是困扰工程界的一大难题，充分利用废弃橡胶，可以减少其对环境造成的巨大危害.将废弃橡胶应用到钢管混凝土中，可以满足结构承载力及变形要求，达到吸收地震能量，减少结构损伤的目的；同时也能解决废弃橡胶的回收利用问题，从而实现资源、环境与建筑三者之间的可持续化发展.

刘锋等[2]通过对低强橡胶混凝土进行单轴压缩试验，发现随着橡胶掺量的增加，橡胶混凝土轴心抗压强度逐渐降低.梁炯丰等[3]对16个圆钢管橡胶混凝土短柱进行轴压试验，发现钢管橡胶混凝土柱破坏形态与普通钢管橡胶混凝土柱类似，随着橡胶取代率的增加和橡胶粒径的增加，其承载力不断降低.刘艳华等[4]通过对8个圆钢管橡胶混凝土短柱进行轴压试验，发现钢管橡胶混凝土柱具有良好的承载能力和抗变形能力，其承载力和刚度与橡胶取代率和粒径有关.

通过对16根圆钢管橡胶混凝土短柱的轴压试验分析研究圆钢管橡胶混凝土短柱轴压承载力的影响因素，根据不同研究理论对圆钢管橡胶混凝土短柱承载力进行试算分析，并提出了适合于圆钢管橡胶混凝土短柱轴压承载力的计算公式.

1 试验概况

在青岛理工大学结构试验室的5000 kN微机控制电液伺服压力试验机上对16根圆钢管橡胶混凝土短柱进行轴压试验，试验参数采用了橡胶取代率w和含钢率α.试验所用的橡胶混凝土设计强度等级为C35，采用等体积取代法分别以取代率w=0%，10%，20%，25%，30%取代细骨料，选用P·O 32.5R水泥，连续级配的中粗河砂，橡胶粒径为0.1～5 mm的连续级配胶粒，表观密度1220 kg/m3.详细配合比及实测混凝土立方体抗压强度标准值如表1所示.设计试件含钢率α分别为0.08，0.10，0.15，0.16，控制长径比L/D=3，宽厚比控制在20～85，套箍系数ζ控制在0.5～2.5.基本参数如表2所示，其中，D组仅用于研究橡胶取代率为25%～30%时构件的承载力发展情况.

试验在弹性范围内按预计极限荷载1/10分级加载，试件屈服后按预计极限荷载1/15分级加载，当试件达到峰值荷载后，改为以2～3 mm/min速率的位移控制加载，直至试件破坏，加载示意与试验设备分别如图1、图2所示.

表1 橡胶混凝土配合比及力学性能

表2 试件设计参数及部分试验结果

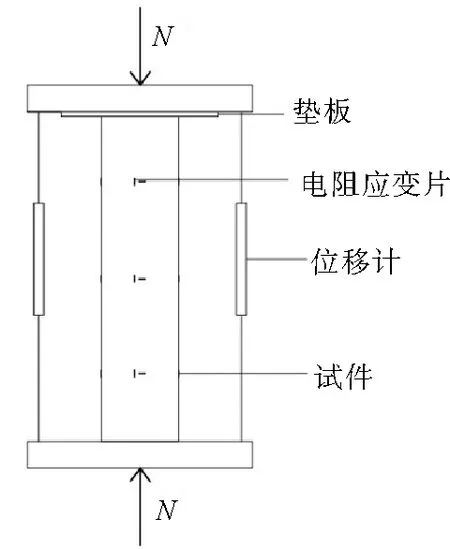
图1 加载示意装置

图2 试验设备

2 试验结果与分析

试验表明，所有试件的试验现象和破坏形态表现出一致性，其轴压试验破坏形态与普通圆钢管橡胶混凝土柱破坏形态类似，均为试件中下部鼓曲破坏.加载初期，试件处于弹性阶段，钢管发生轻微径向变形；随着荷载继续增加，试件发出轻微响声，应变发展较快，随后试件达到屈服进入塑性阶段，试件纵向应变增长较快；随着荷载的增加，试件达到峰值荷载，并出现一处或多处鼓曲，随后试件局部出现明显鼓曲或褶曲，试件破坏形态如图3、图4所示.从图3、图4可以看出虽然圆钢管橡胶混凝土的受压破坏形式与普通钢管混凝土类似，但其达到极限荷载时，塑性变形明显大于普通钢管混凝土，且随着橡胶掺量的增加，其变形量逐渐增大.

图3 w=0%的不同尺寸下试件破坏形态

图4 w=30%的不同尺寸下试件破坏形态

图5为试验所得试件荷载-应变N-ε关系曲线；图6为试件名义应力-应变σscu-ε关系曲线；实测圆钢管橡胶混凝土试件特征点荷载见表2，其中，Ny为试件的屈服荷载，即实测钢管应变达到钢材屈服应变时所对应的荷载；Nu为试件极限承载力，即实测试件峰值荷载.

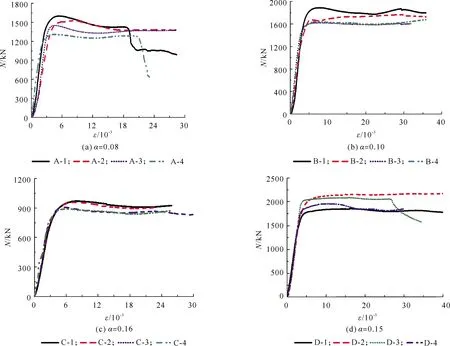
图5 荷载-应变关系曲线(橡胶取代率的影响)

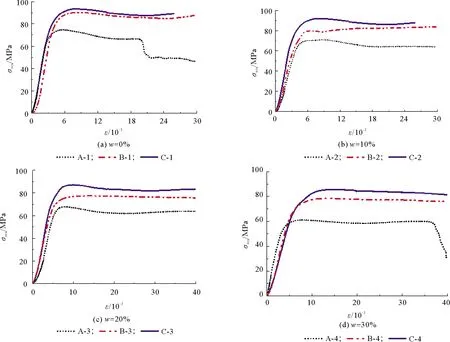
图6 名义应力-应变关系曲线(含钢率的影响)

由表2及图5、图6可知：

1) 随着橡胶取代率的增加，圆钢管橡胶混凝土短柱承载力降低，通过A，B，C组试验可得，橡胶取代率每增加10%，承载力降低率平均值依次为4.91%，9.91%，10.70%；通过D组试验可以得出，橡胶取代率从25%到30%时，试件承载力相差为2.86%，说明橡胶取代率从0%增加到25%时，承载力下降迅速，橡胶取代率由25%增加到30%时，圆钢管橡胶混凝土短柱轴压承载力下降变缓.

2) 通过对比A—C组相同橡胶取代率试件名义极限压应力，可以发现，随着含钢率的增加，圆钢管橡胶混凝土短柱承载力提高，含钢率α从0.08增加到0.10和0.16，对于橡胶取代率为0%的试件，承载力分别增加了15.30%和26.82%；对于橡胶取代率为10%的试件，承载力分别增加了19.09%和36.38%；对于橡胶取代率为20%的试件，承载力分别增加了16.67%和35.13%；对于橡胶取代率为30%的试件，承载力分别增加了21.38%和36.89%.说明当橡胶取代率增大时，内填混凝土的强度降低，含钢率的增加对构件承载力的提高影响较大.

3) 对比每组试件屈服强度与屈强比，可以看出，试件屈强比有增大的趋势，说明圆钢管橡胶混凝土短柱随着橡胶掺量的增加，其安全储备降低.

3 圆钢管橡胶混凝土短柱轴压承载力计算方法

根据试验可以看出圆钢管橡胶混凝土短柱工作机理与普通钢管混凝土短柱类似，因此尝试按普通钢管混凝土短柱承载力计算公式对试件的承载力进行试算.国内外的相关研究成果表明，钢管混凝土承载力计算方法主要有4种：统一强度理论、拟钢理论、拟混凝土理论以及叠加理论.统一强度理论将钢管混凝土视为统一的整体材料，钢管与核心混凝土之间相互作用、协同互补，代表研究成果有韩林海教授的《钢管混凝土结构：理论与实践》[5]以及原电力部《钢-混凝土组合结构设计规范》(DL/T 5085—1999)[6]等；拟钢理论将钢管混凝土折算成钢，再以钢结构规范进行分析计算，代表规程有中国的《矩形钢管混凝土结构技术规程》(CECS 159:2004)以及美国的AISC-LRFD(2005)[7]规范等；拟混凝土理论计算过程中采用“套箍强化”效应，将钢管混凝土等效为钢筋混凝土构件，并根据极限平衡理论进行承载力的分析与计算，主要规程有我国的《钢管混凝土结构技术规范》(GB 50936—2014)[8]以及欧洲的EN1994-1-1(2004)规程[9]等；叠加理论不考虑钢管壁与核心混凝土间的黏结作用，分别将钢管与混凝土所受的承载力叠加，即为其极限状态承载力，代表规程主要有日本的AIJ-CFT(1997)[10]规程.

利用上述规程、规范计算方法，分别计算试件轴压承载力Ni，并与试验得到的承载力Nu进行对比，发现韩林海教授研究成果、《钢-混凝土组合结构设计规范》(DL/T 5085—1999)、《钢管混凝土结构技术规范》(GB 50936—2014)以及EN1994-1-1(2004)规程的Ni/Nu均在0.77～1.08，均值分别为0.873，0.905，0.927和0.816，具有较高的吻合度；CECS 159:2004规程、AISC-LRFD规程及AIJ规程的Ni/Nu范围为0.65～0.83，均值分别为0.718，0.693和0.750，计算结果均小于试验结果，差值较大.

随着橡胶取代率的增加，计算值与试验值偏差逐渐增大，说明现有规程、规范计算方法不能准确反映内掺橡胶对圆钢管橡胶混凝土的承载力的影响，原因在于随着橡胶掺量的增加，混凝土强度持续降低，而套箍系数ζ逐渐变大，钢管壁对内填橡胶混凝土的约束增强，计算值与试验值差值增大.

为进一步判断上述理论回归模型的拟合效果，采用差析法和计算相关指数R2两种方法进行验证.差析法是做出残差图，分析所用回归模型是否恰当，如图7所示.相关指数R2=1-RSS/TSS可用来评价线性回归公式的拟合程度，其中，TSS为总体平方和，RSS为残差平方和，R2越大，RSS越小，说明散点与直线拟合程度越好，稳定性越高.运用拟钢理论和叠加理论得相关指数R2均在0.97以下，残差平方和均在1以上，说明计算值与试验值离散度较大，拟合程度和稳定性欠佳，因为拟钢理论将核心混凝土折算成钢进行简化计算，而忽略了钢管混凝土构件剪切模量的变化，计算偏差较大；而叠加理论忽略了钢管壁与核心混凝土间的套箍约束，计算方法偏于保守；运用拟混凝土理论的《钢管混凝土结构技术规范》(GB 50936—2014)的R2=0.9883，拟合度较好，但欧洲的EN1994-1-1(2004)规程的R2=0.9610，离散度较大；统一强度理论的相关计算方法中韩林海教授研究成果与《钢-混凝土组合结构设计规范》(DL/T 5085—1999)的R2值分别为0.9796和0.9874，说明针对圆钢管橡胶混凝土承载力计算，统一强度理论相关计算方法拟合度最优，拟混凝土理论次之.

4 圆钢管橡胶混凝土短柱极限承载力计算公式

本文在试验数据及相关研究的基础上，基于统一强度理论，将钢管橡胶混凝土视为统一的组合材料，利用钢管橡胶混凝土整体几何特性和组合性能指标计算圆钢管橡胶混凝土短柱的承载力，参照文献[11]的研究思路，提出承载力统一公式：

Nu=fscAsc

(1)

式中：Asc为钢管混凝土横截面积；fsc为钢管混凝土轴心受压强度.

当套箍系数ζ=0.2～5时，引入钢管混凝土强度指标系数γc=fsc/fc来研究fsc与fc的关系，根据试验可知，对于钢管橡胶混凝土构件其性能与普通钢管混凝土构件类似，则假设γc与套箍系数ζ成线性关系，即

fsc=γcfc

(2)

γc=αζ+β

(3)

根据试验结果与式(1)计算圆钢管橡胶混凝土短柱轴心受压强度指标fsc，并根据式(2)计算钢管混凝土强度指标系数γc，根据γc与ζ关系曲线(图8)可线性回归得出α=0.6653，β=1.4748，故圆钢管橡胶混凝土短柱轴压承载力指标系数计算公式可以表达为

γc=0.6653ζ+1.4748

(4)

综上所述，适合于圆钢管橡胶混凝土短柱轴压的承载力计算公式可以表达为

Nu=(0.6653ζ+1.4748)fcAsc

(5)

利用式(5)对试验承载力进行计算，结果如表3所示，N′u为根据式(5)计算所得圆钢管橡胶混凝土短柱试件的轴压承载力，计算结果N′u与Nu试验结果吻合较好，N′u/Nu均值为1.004，方差为0.0051，偏差较小，离散性不大.为进一步验证公式的合理性，分别对梁炯丰[3]、刘艳华[4]等进行的圆钢管橡胶混凝土短柱轴压试验数据进行对比验证，计算结果如图9、表4、表5所示，通过对比不难看出，计算值与试验值偏差较小，N′u/Nu均值分别为0.992和1.071，离散性较小，证明了公式的合理性.

比较图7和图9可知：利用本文公式计算的N′u/Nu残差均在±0.15范围内，3组试验的相关指数R2分别为0.9949，0.9966和0.9934，明显优于现有研究成果及规程、规范，说明本文提出的圆钢管橡胶混凝土短柱轴压承载力计算公式具有更高的精度和稳定性.

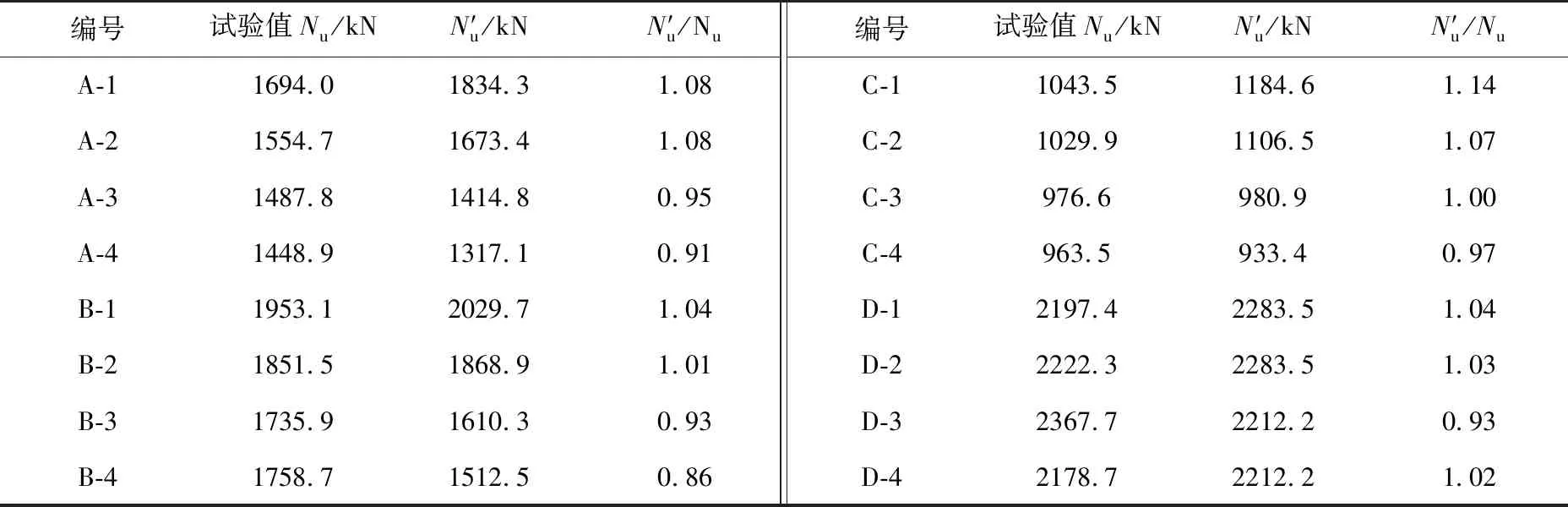
表3 本文承载力计算方法验证

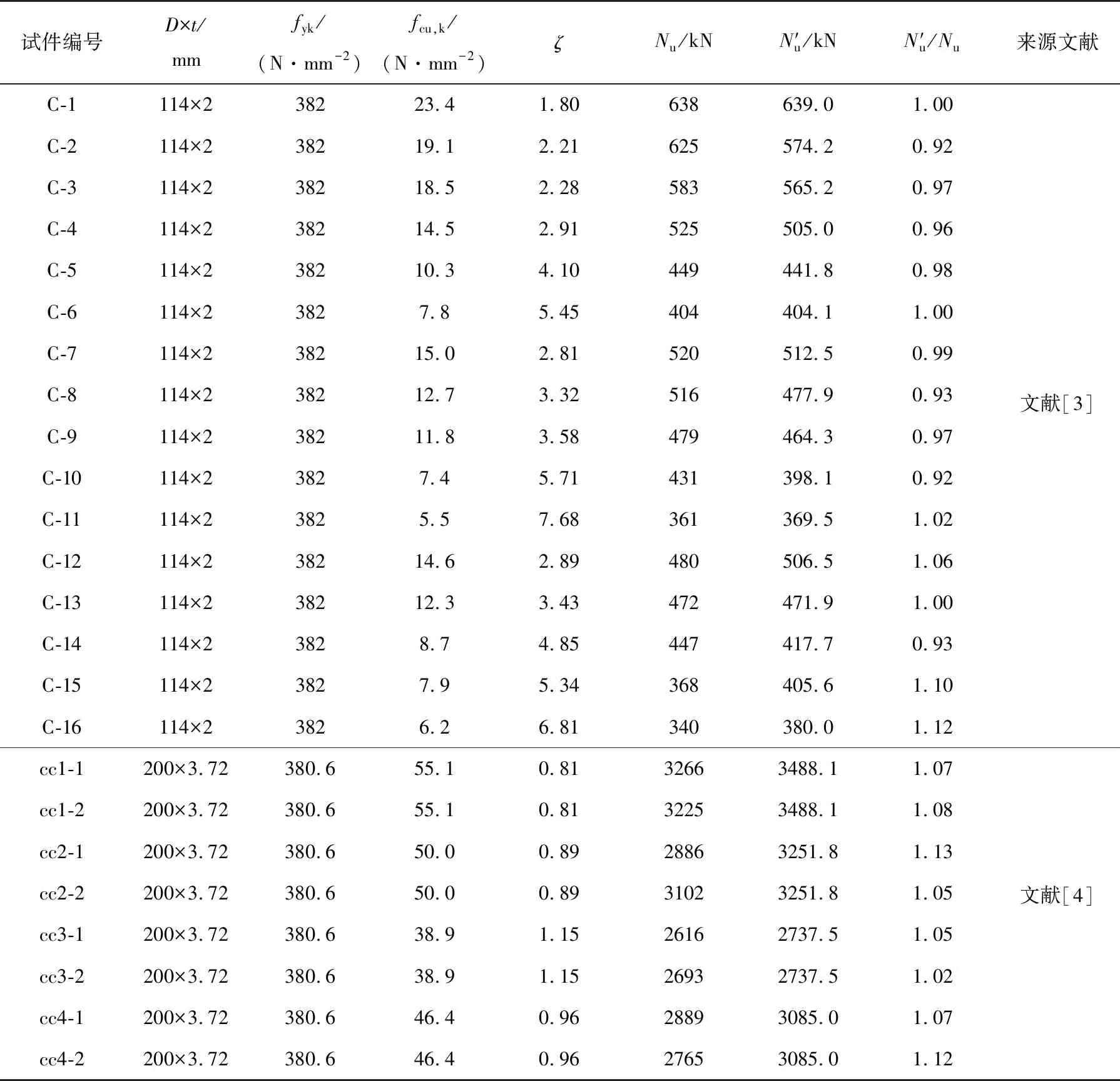
表4 承载力计算公式文献试验验证

表5 试验值与计算值之比的统计特征

5 结论

通过圆钢管橡胶混凝土短柱轴压承载力的试验分析，得出如下结论：

1) 圆钢管橡胶混凝土短柱破坏过程与普通圆钢管混凝土短柱破坏过程相似，破坏形态均为中下部鼓曲破坏，随着橡胶取代率的增加与含钢率的减少，其极限承载力减小，安全储备降低.

2) 采用了现有的研究成果对圆钢管橡胶混凝土短柱承载力进行计算比较，随着橡胶的掺入，偏值逐渐加大，现有普通圆钢管橡胶混凝土短柱承载力计算方法不能准确反映橡胶的掺入对其承载力的影响.

3) 基于统一强度理论，根据试验结果拟合了适用于圆钢管橡胶混凝土短柱承载力的计算公式：Nu=(0.6653ζ+1.4748)fcAsc，其中ζ为套箍系数，fc为混凝土轴心抗压强度设计值，Asc为钢管混凝土横截面积；并采用不同学者试验进行了验证，计算值与试验值吻合度较高，离散性较小，公式可以较精确地预测圆钢管橡胶混凝土短柱的承载力.