一种改进的宽波束线阵雷达物位测量算法
2021-04-30王长元张圆圆
谢 垚,黄 默,王长元,张圆圆,荆 琛
(1.中国科学院 微电子研究所,北京 100029;2.中国科学院大学,北京 100049)
物位测量技术被广泛应用于各种工业场景[1],是生产自动化控制系统重要技术组成。基于天线雷达的物位测量,作为一种非接触式物位测量方式,将距离测量转换为对电磁波在场景中传播时间的测量[2]。因其非接触性,雷达物位测量可替代人工作业[3],可在高温、高压、粉尘场景下实现对腐蚀性、毒性等高危材料物位进行连续测量[4]。天线雷达物位测量通过工作体制可将其分为调频连续波雷达物位测量和脉冲雷达物位测量。相对于脉冲雷达物位测量,调频连续波雷达物位测量具有高距离分辨率、无近端盲区、低功耗等优势,受到越来越多的关注。
由于工业场景的复杂性以及储物料仓结构的特殊性,对料仓内物料物位进行测量时,强杂波对物位测量的干扰不可避免。现有较为成熟的天线雷达物位测量,主要依靠设计窄波束天线,从硬件角度解决杂波干扰问题[5]。如SRTRANS LR460、SRTIANS LR560[6]、OPTIMAVE 6300C[7]等物位测量产品均使用喇叭口天线,其对应的最大3 dB波束宽度分别为11°、4°和10°。窄波束天线可以很好地屏蔽来自料仓侧壁的背景杂波,因此在设计物位测量算法时不需要考虑强杂波对物位测量的影响。从成熟的基于快速傅里叶算法(FFT-Based)的物位测量算法[8],到在其基础上改进的Zero-Padded FFT[9]、快速频率估计算法(Fast Frequency Estimation Algorithm,FFEA)[10]等算法,均可实现基于窄波束的高精度物位测量。
窄波束雷达物位计因设备体积重量大、价格高,故其应用范围受到较大限制,所以小型化、低成本的宽波束雷达物位计具有更广泛的应用场景。然而,与宽波束物位计相适配的物位测量算法并不成熟,将现有的高精度物位算法直接应用于宽波束雷达物位测量存在诸多问题。在宽波束雷达物位测量中,由于天线波束范围增大导致背景杂波干扰增强,当其应用在“瘦高型”料仓时,由料仓侧壁和侧壁上的物料挂壁导致的背景杂波干扰更加严重[11]。在密闭型料仓中由物料表面-料仓壁、料仓壁-料仓壁导致的多次反射也将影响物位测量效果。与此同时,当被测物料介电常数较低时,由物料表面直接反射信号强度甚至会低于背景杂波的强度。若此时,直接将适用于窄波束雷达物位计的测量算法应用在宽波束雷达物位测量中,将会获取较多的冗余干扰点,导致测量错误。因此,提出适用于宽波束雷达的物位测量算法,可从信号处理算法角度突破雷达物位计测量对天线波束宽度的限制,为雷达物位测量技术带来更广阔的应用市场。
综上,基于调频连续波雷达物位测量的基本原理,阐明了在宽波束雷达物位测量中干扰点对物位测量性能的影响。分析了宽波束雷达物位测量场景中强散射点的产生机理,通过强散射点位置属性与料仓尺寸的关系将其进行分类,在此基础上提出一种改进的宽波束线阵物位测量算法。试验采用77 GHz宽波束调频连续波雷达在实际料仓中进行。实验验证了所提改进算法的准确性和稳定性。
1 调频连续波雷达物位计测量原理
对于调频连续波雷达,通过对发射信号频率进行线性调制,产生大时宽带宽线性调频发射信号。控制发射通道和接收通道同时打开实现无盲距测量,发射通道在脉冲宽度T内发射的信号so(t)为
so(t)=ξtexp(j2πf0t+jπKt2) ,
(1)
其中,ξt表示发射信号幅度,f0表示发射信号起始频率,K表示调频斜率。当发射信号作用在物料表面时,电磁波被其反射回雷达接收天线,接收信号si(t)为
(2)
其中,ξr表示接收物料表面信号幅度,R表示物料表面与雷达之间的距离,c表示电磁波传播速度。将接收信号和发射信号经过混频、滤波得到差频信号s(t)为
(3)
其中,ξ表示最终得到的差频信号幅度。从上式可以看到,差频信号为单频信号,测量目标与雷达之间的距离R与差频信号频率成正比。对采样得到的差拍信号进行快速傅里叶变换得到其频谱[12],物位测量值可对频谱进行最大峰值点检测得到,对应的物料表面与雷达之间的距离R为
(4)
其中,fb表示差频信号频率,B表示雷达带宽。而在宽波束雷达物位测量中,由于强背景杂波导致频谱中存在多个强峰值点,甚至部分背景杂波幅值会超过物料表面直接反射信号的幅值,此时,如果直接使用现有物位测量算法,则会得到错误物位测量值。
2 宽波束雷达物位测量强散射点特征分析
现有大部分物位测量算法原理和工程实现均相对简单,可在窄波束情况下实现物位准确测量,但对于宽波束雷达物位测量并不适用。将不同波束宽度雷达在料仓内的物位测量进行图示分析(图 1),图中O表示料仓顶部观察口即坐标系原点,物位计安装在观察口。图中h表示料仓高度,rD表示料仓水平宽度,rs表示观察口与料仓一侧的偏移距离,hv表示物料表面与观察口之间的垂直距离,φ表示雷达水平向3 dB波束宽度。
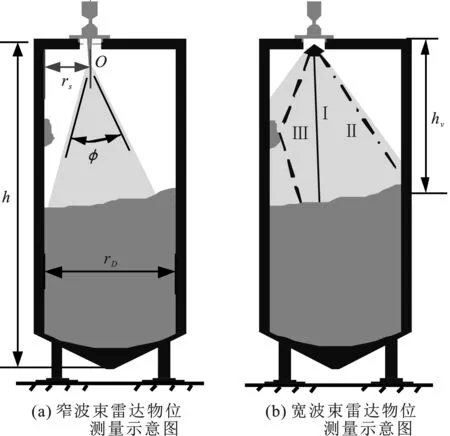
图1 雷达物位测量示意图
当雷达波束宽度较窄时(图 1(a)),主波束全部覆盖在物料表面,料仓侧壁和侧壁上的物料挂壁不会被主波束覆盖,对应的干扰信号弱。同时,窄波束也使得电磁波在料仓内的传播路径简单,减小了多径效应的影响。在“瘦高型”料仓中使用宽波束雷达物位测量时,除了覆盖在物料表面的部分主波束外,其余主波束会覆盖在料仓侧壁和侧壁上的物料挂壁上(图 1(b)),此时现有窄波束物位测量算法将不再适用。
用集合I表示场景中强散射点集合,对某一强散射点而言,可用斜距、角度、幅值三种属性惟一确定。文中基于测量场景中回波信号的产生条件,通过场景中的强散射点位置属性及其与料仓尺寸的关系,将其分为三类。第Ⅰ类强散射点与雷达的水平距离小于料仓的宽度,主要包括物料表面直接反射电磁波形成的强散射点(图 1(b)中实线)。第Ⅱ类为水平距离等于料仓宽度的强散射点,主要包括电磁波被料仓侧壁或侧壁上物料挂壁直接反射形成的强散射点(图 1(b)中短线-点线)。第Ⅲ类为水平距离大于料仓宽度的强散射点,主要包括电磁波在料仓内被多次反射形成的强散射点(图 1(b)中虚线)。强散射点分类判决准则如下。
第Ⅰ类强散射点
I1={p∈I|-(rs-δ)≤Rpsinθp≤(rD-rs-δ)} ,
(5)
其中,I1表示第Ⅰ类强散射点集合,Rp和θp分别表示强散射点P的斜距和与阵列法线夹角,δ为考虑到料仓侧壁上的物料挂壁厚度产生的距离松弛项。
第Ⅱ类强散射点
I2={p∈I|0≤rs-|Rpsinθp|≤δ}∪{p∈I|0≤(rD-rs)-|Rpsinθp|≤δ} ,
(6)
其中,I2表示第Ⅱ类强散射点集合。
第Ⅲ类强散射点
I3={p∈I|Rp|sinθp|>rs}∪{p∈I|Rp|sinθp|>(rD-rs)} ,
(7)
其中,I3表示第Ⅲ类强散射点集合。
在宽波束雷达物位测量时,这些强散射点被分为物位测量有效点和物位测量干扰点。如何从这些强散射点中识别出物位测量有效点,是宽波束雷达物位测量算法需要解决的问题。
3 宽波束线阵雷达改进物位测量算法
在FFT-Based物位测量算法的基础上,结合雷达进行物位测量时获取的强散射点特征分析,提出了一种改进的宽波束线阵雷达物位测量算法,可用于宽波束线阵雷达的物位测量。改进算法由两部分组成,第1部分为强散射点检测及其参数估计,第2部分为强散射点分类及有效点判别。具体处理步骤如图2所示。图中Nc表示强点累积次数。
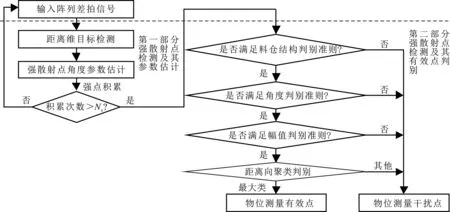
图2 宽波束线阵雷达物位测量算法流程图
3.1 强散射点检测及其参数估计
对于阵列雷达,单信源场景下接收到的阵列差拍信号X(t)为
X(t)=A·s(t)+N(t) ,
(8)
其中,A表示阵列流型矩阵,具体表达形式由雷达阵列结构决定,N(t)代表服从方差为σ2的加性高斯白噪声。在多信源场景中,将s(t)以[s1(t)s2(t) …sK(t)]T代替,其中sk(t)表示参考阵元接收到的信源k对应的差拍信号,K表示场景中的信源个数,上标T表示矩阵转置。对X(t)进行采样,得到阵列差拍信号矩阵。
对X(t)采样后的信号矩阵各个通道进行快速傅里叶变换,得到距离-阵元域矩阵。对于目标距离参数,使用有序统计恒虚警检测算法[13]对各个通道沿距离向进行强散射点检测。而后在多通道进行一致性检测,去除由噪声产生的强散射点,得到强散射点的距离信息。
对于强散射点的角度参数,文中使用脉冲压缩后多重信号分类(APC-MUSIC)算法[14]。算法选取距离-阵元域矩阵中强散射点所在距离门的阵元维数据,计算其协方差矩阵。利用信号子空间和噪声子空间通过谱峰搜索得到强散射点的角度信息。该算法既可实现目标到达角的超分辨估计,突破自由度的限制,又可避免多重信号分类(MUSIC)算法[15]中需要的目标距离、角度配对过程。到达角θ估计公式如下:
(9)
其中,上标H表示矩阵共轭转置,UP表示强散射点P所在距离门的阵元维数据对应的噪声子空间,a(θ)表示与阵列结构有关的阵元导向矢量。
3.2 强散射点分类及有效点识别
时间维积累是提高雷达检测性能的重要手段[16]。为了提高检测性能,在有效点判别前对多次阵列差拍信号中检测到的强散射点进行积累。积累后强散射点集合为Ic。对于集合Ic中的强散射点P,通过目标检测以及参数估计,可得到其距离、角度、幅值信息,点P惟一确定。结合强散射点产生条件,强散射点中有效点的判别算法由料仓结构判别、波束宽度判别、强散射点幅值判别和距离向聚类判别组成。具体判别算法如下。
(1) 料仓结构判别准则
对于所有强散射点中有效点的判别问题,可以认为是一个假设检验问题。对于此问题,以下两种假设必有一成立:强散射点为物位测量有效点(H0),或强散射点为物位测量干扰点(H1)。进行物位测量时,可认为只有第Ⅰ类强散射点集合中的部分点属于测量有效点,第Ⅱ类和第Ⅲ类强散射点均属于物位测量干扰点。通过料仓结构判别准则将大部分Ⅱ类目标点和所有Ⅲ类目标点滤除,判别准则如下:
(10)
(2) 角度判别准则
通过料仓结构判别后,剩余的强散射点集合中包含有第Ⅰ类强散射点和少量第Ⅱ类强散射点。当物料表面与观察口之间的垂直高度hv≤h-max{rs,rD-rs}·tan(φ/2)时,由侧壁直接反射造成的干扰增大。在宽波束雷达物位测量时,可以认为绝大部分物料表面是由主波束覆盖的,测量有效点存在于主波束覆盖的物料表面,所以需要通过一定的角度门限进行判别。角度判别门限由波束宽度决定,判别准则如下:
(11)
(3) 幅值判别准则
通过料仓结构判别和角度判别后,强散射点集合为IL,集合中元素个数为NL。雷达物位计被安装于料仓顶部位置,天线主波束正对物料表面,由物料表面导致的测量有效点幅值相对较大。所以在距离维聚类判别之前进行幅值判别,滤除弱目标点[17],判别准则如下:
(12)
其中,EP表示集合IL中强散射点P的幅值。
(4) 距离向聚类判别
对集合I中的强散射点进行多步判别后,剩余强散射点集合IF,主要包括物料表面直接反射形成的测量有效点、多次反射的强散射点、未识别的侧壁挂壁强散射点以及噪声。结合聚类的思想,对集合IF中的点迹进行垂直距离特征分类。由物料表面直接反射形成的测量有效点满足以下条件:
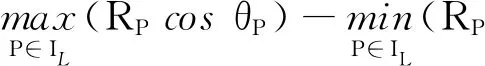
(13)
所以,对集合IF中的强散射点在垂直距离进行分类,距离门限η=rDsinψ,其中ψ表示物料安息角。垂直距离分类后选取元素个数最多的类作为最终物位测量有效点集合Iu,其元素个数为Nu,集合Iu中的强散射点则是由物料表面直接反射形成的强散射点。在测量场景中,当物位发生变化时,强散射点的分布也会发生变化,但是在积累时间内物位只会发生有限的变化。而使用距离向聚类时,当强散射点垂直距离变化不超过分类门限时,均可通过聚类后多个强散射点测量值平均来消除物位变化造成的测量影响。通过对集合Iu中的强散射点垂直距离进行平均,可得到物料表面与雷达物位计之间的垂直距离hv:
(14)
4 算法验证
为验证所提改进算法的有效性,试验在河南某粮食加工厂中的粮仓进行。测量目标为低介电常数物料面粉。在验证阶段,使用了起始频率为77 GHz的调频连续波雷达,所用雷达具体指标见表1。

表1 雷达物位计系统参数
在观察口O不同位置的料仓中对低介电常数物料面粉进行物位测量,测试料仓的结构参数h,rD,rs的定义见表2,表中量尺测量值hv为观察口正下方位置物料表面处物位实测值。

表2 实测料仓参数 m
算法验证由3部分组成:(1) 分析两个实测料仓回波,通过实测数据说明宽波束雷达物位计测量低介电常数物料时的难点;(2) 分析单次测量时两料仓中强散射点二维分布情况,证明改进的宽波束线阵雷达物位测量算法的准确性。(3) 在实际料仓中进行60次连续测量,同时与FFT-Based物位测量算法进行对比,证明改进的宽波束线阵雷达物位测量算法的稳定性,同时还通过多次测量构建了两种场景下的物料表面起伏情况。通过(2)和(3)的验证,说明了所提改进的宽波束线阵雷达物位测量算法的有效性。
4.1 料仓实测回波分析
图3为料仓1和料仓2的归一化距离向回波,图中近端强散射点是由收发通道串扰造成的。图 3(a)为料仓1回波,在不考虑近端收发通道串扰的情况下,图中共有三处分散的强散射点(椭圆框标记),最强点对应的距离为3.1 m,与实测值10.0 m之间存在较大差异。在料仓1中,物料表面与观察口之间的实测距离为10.0 m,而其料仓水平宽度只有3.0 m。在这样的实测条件下,对于水平向3 dB波束宽度为56°的雷达而言,其主波束只有30%直接覆盖在物料表面,故在料仓1中侧壁将存在大量回波。此时,部分干扰点的幅值超过了物料直接反射回波强度,此时使用FFT-Based物位测量算法将会得到错误物位测量值。
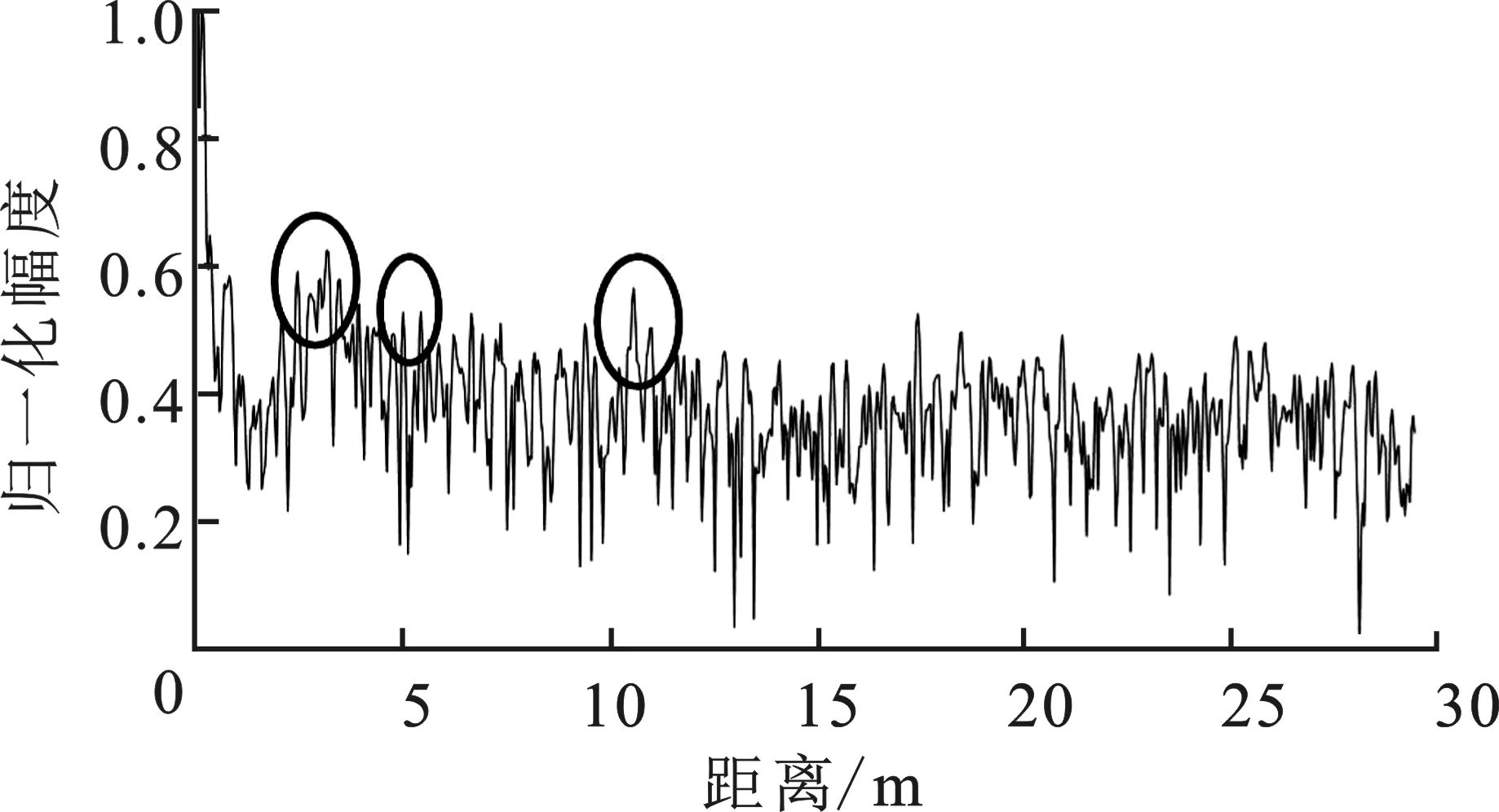
(a) 料仓1距离向回波
(a) 料仓1强散射点分布
图 3(b)为料仓2回波,图中只有一处强散射点。使用FFT-Based物位测量算法得到的物料表面与观察口距离为3.2 m,与实测值吻合。在料仓2中,物料表面与观察口之间的实测垂直距离约为3.0 m,料仓水平宽度为4.0 m,观察口偏移尺寸为3.2 m,对于水平向3 dB波束宽度为56°的雷达而言,其主波束的77%将直接覆盖在物料表面,类似窄波束时物位测量情况。故回波信号中由物料表面直接反射形成的信号较强,干扰点回波较弱。
通过对实测数据进行分析,可以看到相比于窄波束雷达物位测量,宽波束雷达物位测量时背景杂波干扰更严重,物位测量难度也将更大。
4.2 算法有效性验证
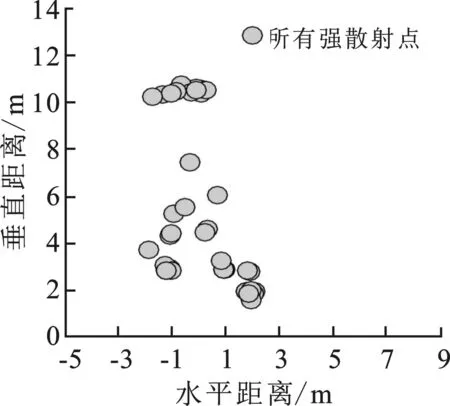
图4显示的是在料仓1和料仓2中进行单次检测时,有效点判别前后强散射点二维分布。处理中阵列差拍信号积累次数Nc= 4,判断强散射点所属类时,所设置的距离松弛参数δ=0.3 m。
料仓1和料仓2中所有强散射点分布如图 4(a)和(d)所示,所得强散射点个数分别为44和32。在图 4(b)和(e)中显示的是在料仓1和2中对强散射点进行分类的结果,料仓1和料仓2中第Ⅰ、Ⅱ和Ⅲ类强散射点个数分别为23、7、14和26、6、0。经过强散射点中干扰点滤除,识别物位测量有效点(图 4(c)和(f)),料仓1和料仓2中最终识别到的有效点个数分别为6和10。统计最终有效点物位信息,得到实测料仓1和2中物料表面与观察口的垂直距离,分别为10.4 m和2.6 m。与量尺实测值10.0 m和3.0 m相比,实现了误差范围内的准确测量。
(a) 料仓1连续测量结果
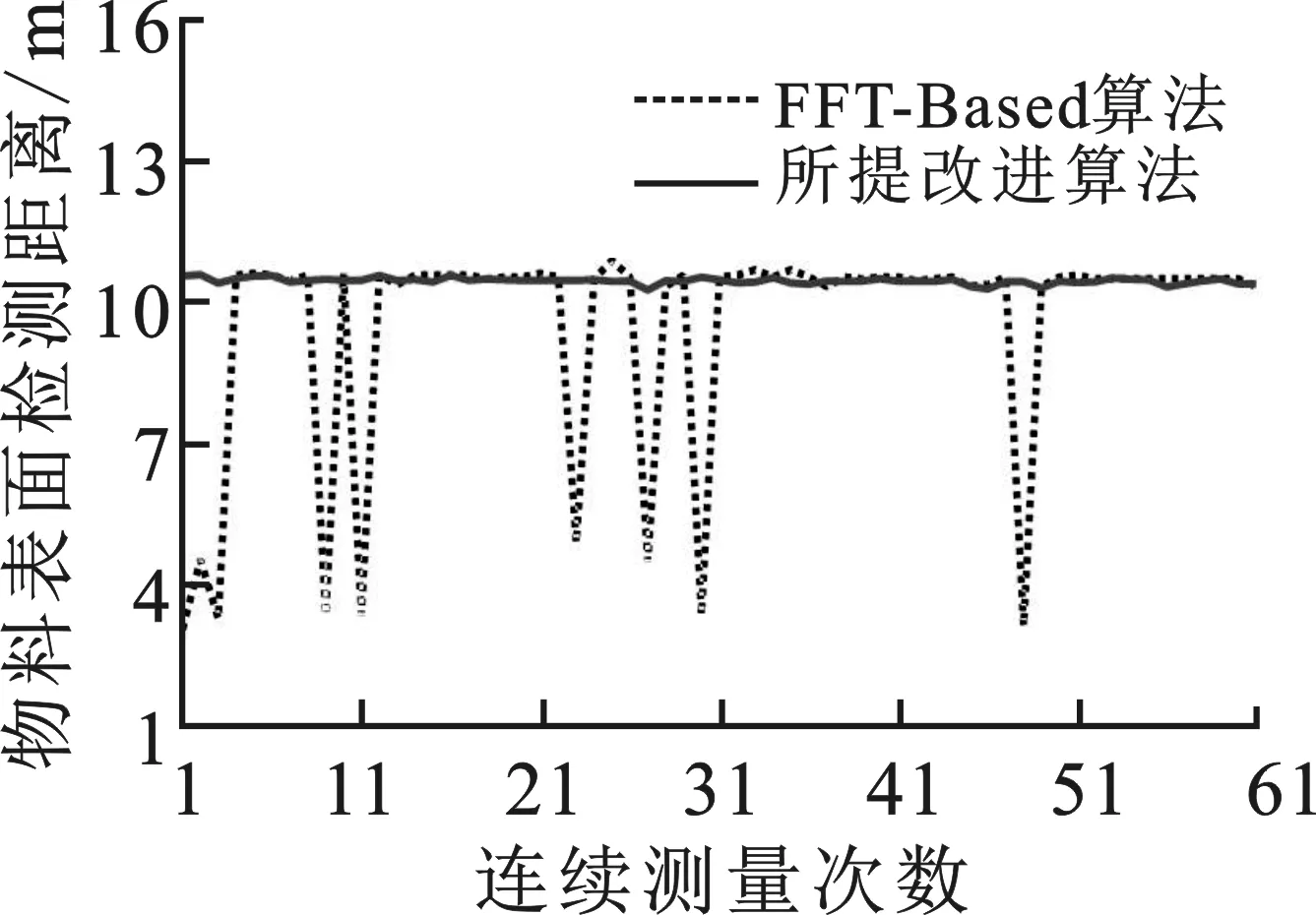
图5显示的是在料仓1和料仓2中进行60次连续测量的结果。由图 5(a)可以看到,在料仓1中进行的连续测量中,直接使用FFT-Based物位测量算法无法得到物位的连续准确测量,物位测量值出现了跳动。而使用所提改进测量算法可以准确地持续地测量物位,测量值未出现跳动,在60次连续测量中,物位测量值方差为0.004 2。而在图 5(b)中,可以看到使用FFT-Based物位测量算法和所提改进的宽波束线阵雷达物位测量算法都可以得到物位的稳定测量,但是改进算法之间有一个固有偏差。其原因为,使用FFT-Based物位测量算法进行测量时,得到的距离是物料表面回波最强点与物位计之间的斜距,大于实际的垂直距离。使用改进测量算法在料仓2中进行的60次连续测量时,物位测量值方差为0.005 6。
进行多次测量的有效强散射点积累后,对这些强散射点进行拟合,得到图 6所示的两个料仓中物料表面起伏示意图。其中料仓1的垂直起伏范围为10.4 m至10.7 m,料仓2的垂直起伏范围为2.5 m至3.2 m。从图6中可以看到,两个料仓物料表面起伏特性不同,这是由于两个料仓的进料口位置不同导致的。通过使用宽波束雷达物位计,结合所提改进算法,得到的物料表面起伏图可以实现更精确的物位测量。
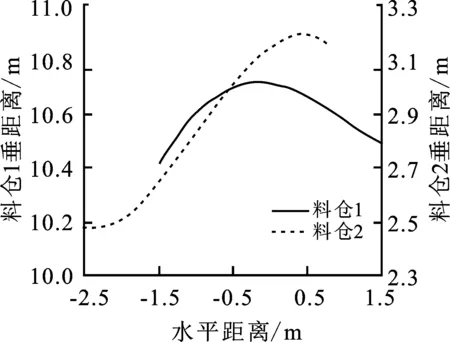
图6 实地料仓物料表面起伏示意图
5 总 结
基于宽波束物位测量时强散射点的分布情况,在FFT-Based物位测量算法的基础上,提出一种改进的宽波束线阵雷达物位测量算法。首先,通过强散射点检测及到达角估计,得到强散射点的距离、幅值、角度信息;然后,使用强散射点有效点判别算法,通过多步判别准则将强散射点分为物位测量有效点和物位测量干扰点,基于有效测量点的物位信息得到物料表面与物位计之间的垂直距离。在某粮仓中使用77 GHz宽波束线阵雷达进行了实地测试,验证了所提改进算法在实地料仓中对低介电常数物料物位测量时的准确性和稳定性。从算法角度突破了雷达物位测量时对雷达波束宽度的限制,对小型化、低成本的宽波束雷达物位计的普及应用具有重要意义。
