一种多目标与多基地雷达之间的博弈策略

赫 彬，苏洪涛

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

随着现代科技的发展，多基地多输入多输出(Multiple-Input Multiple-Output，MIMO) 雷达作为一种新体制雷达系统已经成为了研究热点[1-2]。由于多基地多输入多输出雷达在目标检测、跟踪与定位以及抗干扰等方面表现出了比单基地多输入多输出雷达更优越的性能，受到了各军事强国的高度关注。为了更好地提升多输入多输出雷达的抗干扰能力和覆盖范围，分布式多基地多输入多输出雷达系统被作为主要的研究方向[2]。而对于工作中的多基地雷达系统，雷达之间会产生合作与冲突的博弈关系。为了降低雷达之间的冲突影响，需要对雷达的资源和站址进行合理的布置来提升多基地雷达之间的协作能力，进而提升雷达对目标和干扰机的抵御能力。博弈论作为一种合作与非合作的分析理论，可被应用于处理多基地多输入多输出雷达的资源分配和站址布置等问题当中[3]。

近期，许多学者将博弈理论引入到雷达对抗研究的不同方向[4-14]，其中包括功率分配[4-8]、目标检测[9-10]、目标跟踪与定位[11]、编码和波形设计[12-13]以及雷达通信一体化[14]等。对于功率分配问题，文献[6]研究了智能干扰机与多输入多输出雷达之间功率分配博弈，并构造了两种非合作博弈模型：一种是两人零和博弈；另一种是斯塔伯格博弈，通过数值实验验证了这两种博弈都收敛到博弈的均衡状态。文献[8]利用合作博弈研究了多基地多输入多输出雷达在目标跟踪和定位中的功率分配问题。在目标检测方面，文献[9]构造了一种联合检测概率与虚警概率的效用函数，针对不同场景提出了多种博弈方案，通过超模理论验证了这些博弈属于超模博弈，最后博弈都收敛到纯策略的纳什均衡。与文献[9]不同，文献[10]的作者依据潜博弈论设计了一种极化多输入多输出雷达目标检测方法，该方法较单一的水平极化或垂直极化有更好的检测性能。在目标跟踪方面，文献[11]提出了一种新颖的联合并行粒子滤波和数据关联的博弈算法，该算法在跟踪多个机动目标的情况下表现出了比其他粒子滤波算法更优越的性能。为了更好地抑制干扰的影响，博弈论被作为一种有效的策略分析理论应用于雷达波形的设计当中，这样可以有效地提升雷达的战场性能和存活能力[12-13]。雷达通信一体化是近期的一个研究热点，雷达和通信作为两种不同系统存在着合作与冲突的关系，为了减少二者在实际工作中的相互影响，通过博弈论分析策略使二者保持在一种稳定的状态，提升二者之间协同工作能力[14]。

笔者在研究了凸优化和博弈论的基础上，分析了一种多基地雷达之间的博弈优化模型。首先，构造了一种多基地多输入多输出雷达的博弈框架，在此基础上建立了信干噪比(Signal to Interference Noise Ratio，SINR) 约束的极小化发射功率优化模型。然后，利用拉格朗日对偶理论求得雷达发射功率的迭代公式，利用博弈论分析验证了雷达发射功率满足标准函数，并收敛到博弈的纳什均衡。进一步，通过线性约束最小方差(Linearly Constrained Minimum Variance，LCMV) 准则得到接收波束成形器权矢量，并提出了一种联合波束成形和功率分配的博弈算法。最后，数值实验验证了算法的有效性和抑制互雷达干扰的能力。

1 系统模型

多基地雷达是由K个分离的多输入多输出雷达构成，并且每个多输入多输出雷达由相同的M个收发天线构成。每个雷达都希望自身花费最少的功率来满足一个期望的信干噪比约束。假定所有的雷达属于同一方，并且所有的目标属于敌对的另一方。另外，目标位于多基地多输入多输出雷达的远场环境。对于杂波的干扰影响，可以通过动目标显示和动目标检测来抑制。基于雷达之间的先验信息，雷达可以通过自适应波束成形来抑制它们之间的互干扰影响，这样可以确保雷达更好地检测目标。接下来，在多基地多输入多输出雷达中，第k个雷达主波束指向第l个目标的预编码波形序列skl(t)(k=1，…，K；l=1，…，L)，t为雷达脉冲时间指数。第k个雷达发射的预编码波形矢量sk(t)=[sk1(t)，…，skL(t)]T。对于多输入多输出雷达，满足波形的正交性条件如下：

(1)

其中，Tp为雷达发射脉冲宽度；上标*表示矢量的共轭运算；τkl为正交波形可接受的延时。

接下来，第k个雷达发射到第l个目标的信号形式如下：

xkl(t)=wt(kl)skl(t) ，

(2)

其中，wt(kl)为第k个雷达主波束指向第l个目标复发射波束权矢量。第k个雷达的全部发射信号为

(3)

进而，第k个雷达经第l个目标方向角θkl的反射信号可以写为

(4)

其中，βl为第l个目标的雷达横截面积的散射幅度。第k个雷达的全部接收信号为

(5)

(6)

(7)

(8)

(9)

其中，wr(kl)为第k个雷达对第l个目标的M×1复接收波束权矢量；βkil为从第i个雷达到第k个雷达的经过第l个目标的雷达横截面反射系数；a(θk)和b(θk)分别为第k个雷达发射和接收导向矢量，即

a(θk)=[1 ejd2π/λsin(θk)… ej(M-1)d2π/λsin(θk)]T，

b(θk)=[1 ejd2π/λsin(θk)… ej(M-1)d2π/λsin(θk)]T，

其中，d为阵元间距，所有雷达都是相同的。

多输入多输出雷达的接收端利用匹配滤波来接收期望的目标信号，但这仍会存在一些干扰的影响。因此，通过第k个雷达对第l个目标的回波信号进行匹配滤波可以得到：

(10)

其中，ρklij(τlj)是第i个雷达发射到第l个目标的波形与第k个雷达发射到第j个目标的波形的相关因子。进一步，第k个雷达通过自适应波束成形对第l个目标的回波进行处理，并得到期望输出为

(11)

由于多目标和交叉通道的干扰影响，会降低雷达的目标检测能力。因此，通过自适应波束成形压制的干扰表示为

(12)

进一步，第k个雷达对应于第l个目标的输出信干噪比可以表示为

(13)

其中，‖·‖表示欧氏范数。

2 策略博弈论框架

2.1 博弈的基本模型

一种多基地多输入多输出雷达之间的联合功率分配和波束成形的博弈论框架被建立。由于多基地雷达在对目标进行检测的时候，避免不了会产生互雷达干扰，这样可以利用策略的非合作博弈进行处理。为了提高雷达的工作效率，需要通过自适应波束成形来抑制互雷达干扰。对于该策略非合作博弈，每个多输入多输出雷达被作为参与者，其对应的发射功率和权矢量作为相应的博弈策略。而雷达的总发射功率被作为效用函数。因此，博弈框架被表示为

G={P，S，U} ，

(14)

(1) 参与者集：P={Rk|k=1，2，…K}；

其中，pR(kl)为第k个雷达对应于第l个目标的发射功率；1L表示长度为L的全1列矢量。

在分析策略博弈时，给定了其它雷达的波束策略，每一个雷达都希望自身花费最小的代价，并能实现对目标的准确检测。由于每个雷达是自私的，在抑制其它雷达的直接干扰的同时，又能够极小化自身的发射功率。根据预设的信干噪比准则，建立第k个雷达的波束成形和约束信干噪比的优化模型，即

(15)

2.2 纳什均衡分析

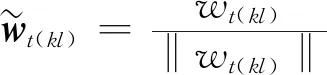
(16)

针对上述功率分配博弈模型，为了验证博弈G的纳什均衡的存在性和唯一性，需要证明每个参与者的最佳反应策略满足标准函数的定义。为了获得最优的发射功率分配策略，问题(16)的不等式约束可以用等式约束来替换，且满足最小的信干噪比准则；同样地，满足更大的信干噪比需求。因此，等式形式如下：

(17)

进一步，式(17)可以表示成下面的矩阵形式：

(18)

(19)

根据Arrow-Debreu定理，上式的解的存在性被满足[7]。进一步，纳什均衡的唯一性被验证通过最佳反应函数为标准函数。因此，引入标准函数的定义：

(a)恒正性：对于全部的x>0，则有I(x)>0；

(b)单调性：若x′>x，则I(x′)>I(x)；

(c)扩展性：对任意a>1，则aI(x)>I(ax)。

另外，从第i个雷达到第k个雷达的其他目标信号干扰矩阵可以表示为Hki∈L×L和其对应元素为因此，将干扰矢量分解，得到雷达k的最佳反应策略函数为

(20)

定理最佳反应函数式(20)满足标准函数的以下3条性质。

总之，本节构造了一个多基地多输入多输出雷达与多目标之间的博弈论框架。在一个确定的信干噪比约束下，建立了联合功率分配与波束成形的优化模型，并验证了博弈的纳什均衡的存在性和唯一性。

3 联合功率分配和波束成形博弈

3.1 功率分配

雷达为了在博弈过程中获得更大的优势，每个参与者都期望获得其他参与者的通道信息。由于多基地雷达属于同一组织的参与者，所有互雷达通道信息参与者都相互了解，并且每个雷达都了解其他雷达的确切位置。问题(15)是一个二次约束二次规划问题，可以通过拉格朗日对偶理论来求解，则拉格朗日函数为

(21)

其中，λkl，υkl为拉格朗日乘子。进一步，拉格朗日函数可以重新写为

(22)

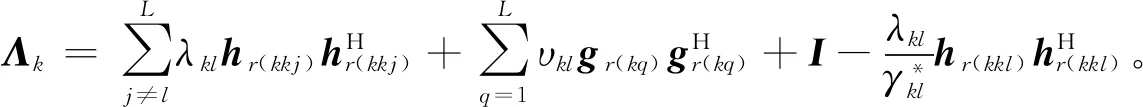
因此，可以得到拉格朗日对偶函数：

(23)

进而，若Λk不是半正定矩阵，则存在wt(kl)的集合使得对偶函数gk(λk，υk)=-∞。问题(16)的对偶问题为

(24)

(25)

然后，再由上式可以得到最优λkl一个必要条件如下：

(26)

根据强对偶定理，主优化问题的最优值等于对偶问题的最优值。因此，可以得到如下的结果：

(27)

另外，η-kl为一个有界的能量值。因此，式(26)和式(27)可以通过变量替换得到雷达的功率分配公式；该式满足标准函数的三条性质，迭代地收敛到一个固定的点。

3.2 波束成形优化

对于回波信号模型，不考虑杂波和其他有源干扰。在接收端对互雷达通道干扰利用自适应波束成形算法进行抑制，通过线性约束最小方差准则来求解雷达的最优接收权矢量：

(28)

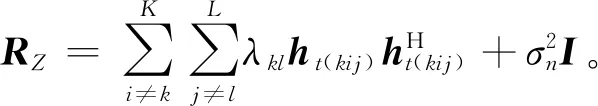
(29)

进而，利用拉格朗日乘子法可以得到接收波束成形权矢量：

(30)

根据文献[7]，发射波束成形权矢量和接收波束权矢量存在一个尺度系数的关系，即

(31)

其中，δkl是一个标量因子，是通过式(15)的信干噪比不等式约束的最优等式约束所得到的。将式(31)代入式(15)中的信干噪比等式约束形式，可以得到下式：

(32)

最后，提出一种迭代的联合功率分配和波束成形博弈算法，算法如下。

算法1联合功率分配和波束成形博弈算法。

① 输入：参数和初始功率。

② 执行。

③ 根据式(27)，更新pR(kl)。

④ 根据式(30)，更新wr(kl)。

⑤ 根据式(31)，更新wt(kl)。

⑦ 输出：pR(kl)，wr(kl)，wt(kl)。

4 数值模拟

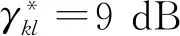
图1 本文算法对不同目标的功率分配收敛图

图2 均衡状态下总功率消耗对比

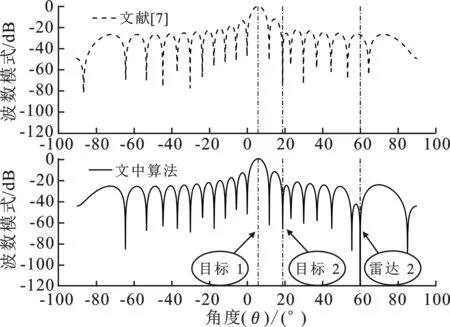
图3 雷达1的主波束指向目标1

图4 雷达1的主波束指向目标2

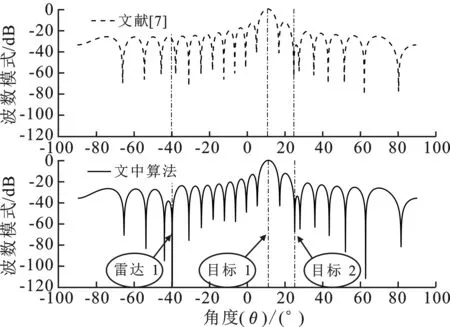
图5 雷达2的主波束指向目标1

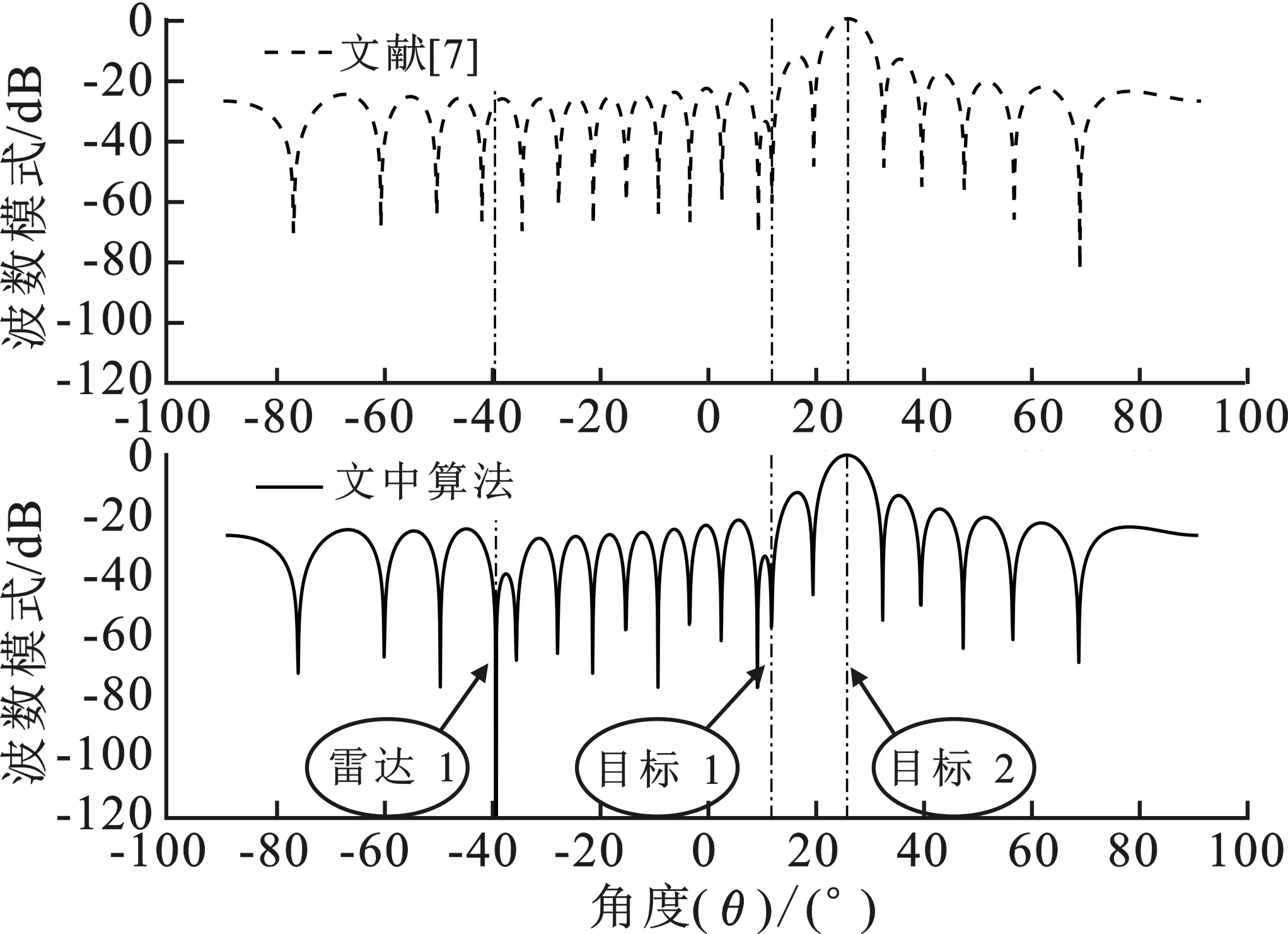
图6 雷达2的主波束指向目标2

5 结束语

笔者研究了一种多基地雷达与多目标之间的博弈模型。首先，根据每个雷达需求和约束构造了多基地多输入多输出雷达的信号系统模型。然后，基于每个雷达的自私性，建立了一种策略非合作博弈论框架；依据该框架构造了一种确定信干噪比约束的极小化发射功率优化模型，并利用凸优化和博弈论得到了纳什均衡的存在性和唯一性。接下来，提出了一种联合功率分配和波束成形博弈算法。该算法通过对不同目标的功率分配来调整波束成形器权矢量，进而对不同方向的干扰进行有策略的抑制。对于外部的强干扰方向可以通过增大雷达发射功率进行有效的抑制，而对于同一方的雷达方向，可以降低发射功率以减少相互之间的干扰，这样针对不同方向上的干扰类型可以通过调整雷达发射功率和波束成形权矢量策略进行有效的抑制。最后，通过数值仿真验证了算法的收敛性和可行性，并较相关的博弈算法有更优越的性能。在将来，笔者将应用合作博弈对多基地雷达系统的协作关系进行分析和研究，并应用更先进的波束成形算法作进一步的研究。