用于三维散射中心SBR建模的边缘绕射修正

陆金文，闫 华，殷红成，张 磊，董纯柱

(北京环境特性研究所 电磁散射重点实验室，北京 100854)

在高频区，雷达目标总的电磁散射可以由多个局部散射源的响应相干合成，这些局部散射源被称为散射中心[1]。这些散射中心通常都与特定的散射机理相对应，如镜面反射、边缘绕射等。散射中心的参数化模型具有形式简单、稀疏以及与散射机理和目标属性相关等优点，广泛应用于高分辨成像[2-4]、数据压缩与重建[5-7]、雷达目标识别[8-11]等领域。与一维、二维情形相比，三维散射中心模型更能完整描述目标散射中心的空间分布，研究目标三维散射中心建模方法具有重要的学术和应用价值。

基于电磁仿真计算的散射中心建模主要包括逆向方法和正向方法。逆向建模是在已知散射数据和确定模型形式的条件下实现模型参数反演的方法[12-15]，通常需要计算大量的扫频、扫角雷达截面积(Radar Cross Section，RCS)幅相数据，计算效率不高。而正向建模方法充分利用目标的精确几何知识和电磁散射机理来确定模型参数[16-23]，在计算效率方面有较大优势。文献[16]在弹跳射线(Shooting and Bouncing Ray，SBR)技术的基础上推导了图像域射线管积分(Image Domain Ray Tube Integration，IDRTI)公式，能够在点频、单视角下快速生成目标的三维逆合成孔径雷达(Inverse Synthetic Aperture Radar，ISAR)图像，并利用迭代峰值搜索算法在ISAR像中提取目标的三维散射中心。文献[17]通过调整ISAR像生成公式中射线扩散函数的形式，在不增加计算复杂度的情况下能够提高ISAR像的质量，减少散射中心的提取时间。文献[18]也提出一种基于弹跳射线技术的海面舰船目标三维散射中心快速建模方法，利用提取的散射中心能够重建精度较高的一维距离像和二维ISAR像。朱国强等人率先提出了基于部件分解与射线分集的属性散射中心参数正向推算方法[19]，并陆续实现了三维散射中心位置的精确修正[20]和正向建模的自动化处理[21]。尽管如此，由于上述基于射线追踪的散射中心建模方法只考虑了目标的物理光学(Physical Optics，PO)贡献，而物理光学无法描述真实边缘绕射的贡献，故针对边缘绕射形成的散射中心，基于这些方法获得的模型存在较大的误差。另外，LI等人[22]提出了基于全波法计算的感应电流分布的散射中心建模方法，BUNGER[23]也利用全波法实现了目标的三维ISAR像快速生成和散射中心提取。尽管上述基于全波法的散射中心建模方法能够精确计算边缘绕射形成的散射中心的模型参数，但其计算效率不高，且难以解决多次散射机理的散射中心建模问题。

针对上述问题，综合考虑目标镜面反射与边缘绕射的贡献，将IDRTI和等效边缘电磁流(Equivalent Edge Currents，EEC)方法相结合，提出了一种针对基于弹跳射线技术的三维散射中心建模的边缘绕射修正方法。针对立方体、圆柱体、球头锥和带尾翼的球头锥-圆柱-圆台组合体(带翼组合体)四类导体目标，进行了实验。实验结果表明，该方法能够有效提高三维散射中心的提取精度。

1 基于IDRTI技术的三维散射中心提取方法

在平面波入射情况下，根据物理光学方法，目标表面远区散射电场可表示为

(1)

弹跳射线是一种标准的射线追踪技术，广泛用于高频区复杂目标的电磁散射计算[24]。弹跳射线技术的主要步骤是首先向目标区发射大量平行射线，然后利用几何光学原理追踪并计算射线在目标表面弹射的路径以及电磁场传输，最后利用上述物理光学公式计算出射点的散射贡献。利用弹跳射线技术，将IDRTI公式三维扩展并改进后，YUN等人的三维ISAR像快速计算公式[17]为

(2)

其中，下标m表示射线的序号，*表示卷积运算，δ(·，·，·)表示三维狄拉克函数，z、x、y表示径向距离和两个正交的横向距离，zm表示径向的总距离延迟，横向位置xm、ym为第一次和最后一次弹射点横向位置的平均值，αm表示每根射线物理光学贡献的复幅度值。h(x，y，z)为射线扩散函数，可表示为

h(x，y，z)=sinc(Δk·z)sinc(k0Δφ·x)sinc(k0Δθ·y) ，

(3)

其中，Δk、Δφ、Δθ表示波数带宽和两个横向的角宽度。

获得三维ISAR像后，利用CLEAN[25]算法可以提取目标的三维散射中心。CLEAN是一种迭代峰值搜索算法，通过逐次搜索残余图像中的峰值点来提取对应的散射中心，然后从图像中剔除该散射中心的点扩散响应。假设第i次迭代提取的散射中心幅度和位置参数为Ai、(xi，yi，zi)，则残余图像可表示为

Ri+1=Ri-Aih(x-xi，y-yi，z-zi)。

(4)

2 用于三维散射中心建模的边缘绕射修正方法

YUN等人的三维ISAR像计算公式(式(2))只考虑了目标的物理光学贡献，笔者利用EEC方法对弹跳射线技术中的单次边缘绕射贡献进行修正，即

E=EPO+EEEC。

(5)

根据EEC方法，任意边缘C的远区绕射场可表示为

(6)

对于三角面元模型，边缘C可以用若干根足够短的直线段来逼近，式(6)中积分可以离散为照明区多段直边缘的积分之和。在每小段直边缘内，Ie和Im为常数，将其提到积分号外，则式(6)可简化为

(7)

其中，

(8)

下标n表示每小段直边缘的序号，rn、ln表示第n段直边缘的中点位置矢量和长度。

ISAR像与远区散射场之间存在傅里叶变换关系，对绕射场作三维傅里叶变换，则三维ISAR像可表示为

(9)

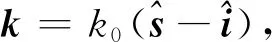
将式(7)代入式(9)，交换求和与积分运算的顺序，可得

(10)

(11)

进一步求解积分，可得

sinc[Δk(z-zn)]sinc[k0Δφ(x-xn)]sinc[k0Δθ(y-yn)]}。

(12)

参考YUN方法[17]，将式(12)转化为卷积形式，并与式(2)相结合，则最终考虑边缘绕射修正的三维ISAR像计算公式为

(13)

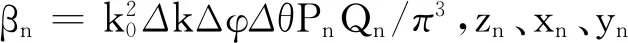
获得考虑边缘绕射修正的三维ISAR像后，同样利用CLEAN算法(式(4))可以提取目标的散射中心，实现考虑边缘绕射修正的三维散射中心建模。

3 实验结果与分析

针对立方体、圆柱体、球头锥和带翼组合体四类导体目标，分别利用BHALLA方法[16]、YUN方法[17]和本文方法提取目标的三维散射中心，通过对比散射中心重建的与仿真的雷达截面积曲线及ISAR像来验证本文方法的有效性。仿真法利用基于弹跳射线技术的高频电磁软件直接计算目标的雷达截面积数据。

立方体的几何模型和雷达截面积曲线如图1所示，尺寸为1 m×1 m×1 m。散射中心提取条件为：俯仰角90°、方位角0°～180°(1°间隔)、垂直-垂直极化、中心频率10 GHz，ISAR空间三个方向的长度均为3 m，采样点数均为64，计算ISAR像的带宽为1 GHz，两个角宽度均为6°，CLEAN算法的相对阈值(相对最强散射中心幅度下降)30dB。以仿真的雷达截面积为参考基准，BHALLA方法和YUN方法散射中心重建的雷达截面积均方根误差为5.91 dB和4.97 dB，而本文方法的均方根误差为0.97 dB。从图1(b)中可看出，在方位角0°、90°和180°附近，立方体平面的镜面反射为主要贡献，BHALLA方法、YUN方法和本文方法散射中心重建的雷达截面积均吻合得较好。但随着方位角逐渐偏离垂直镜面方向，直边缘绕射成为主要贡献，BHALLA方法和YUN方法重建的雷达截面积存在较大偏差。

(a) 几何模型

YUN方法和本文方法在方位角135°下的散射中心模型重建的ISAR像如图2所示，两幅ISAR像均能准确反映直边缘散射中心的位置。YUN方法重建的ISAR像中直边缘绕射强度分别为-6.21 dBsm、-12.54 dBsm和 -12.54 dBsm，而本文方法重建的ISAR像中对应直边缘绕射强度为-2.07 dBsm、-19.72 dBsm 和 -19.72 dBsm，本文结果更符合立方体的直边缘绕射机理。雷达截面积曲线及ISAR像综合对比结果表明，本文方法提取的散射中心能较好地描述立方体直边缘的散射贡献。

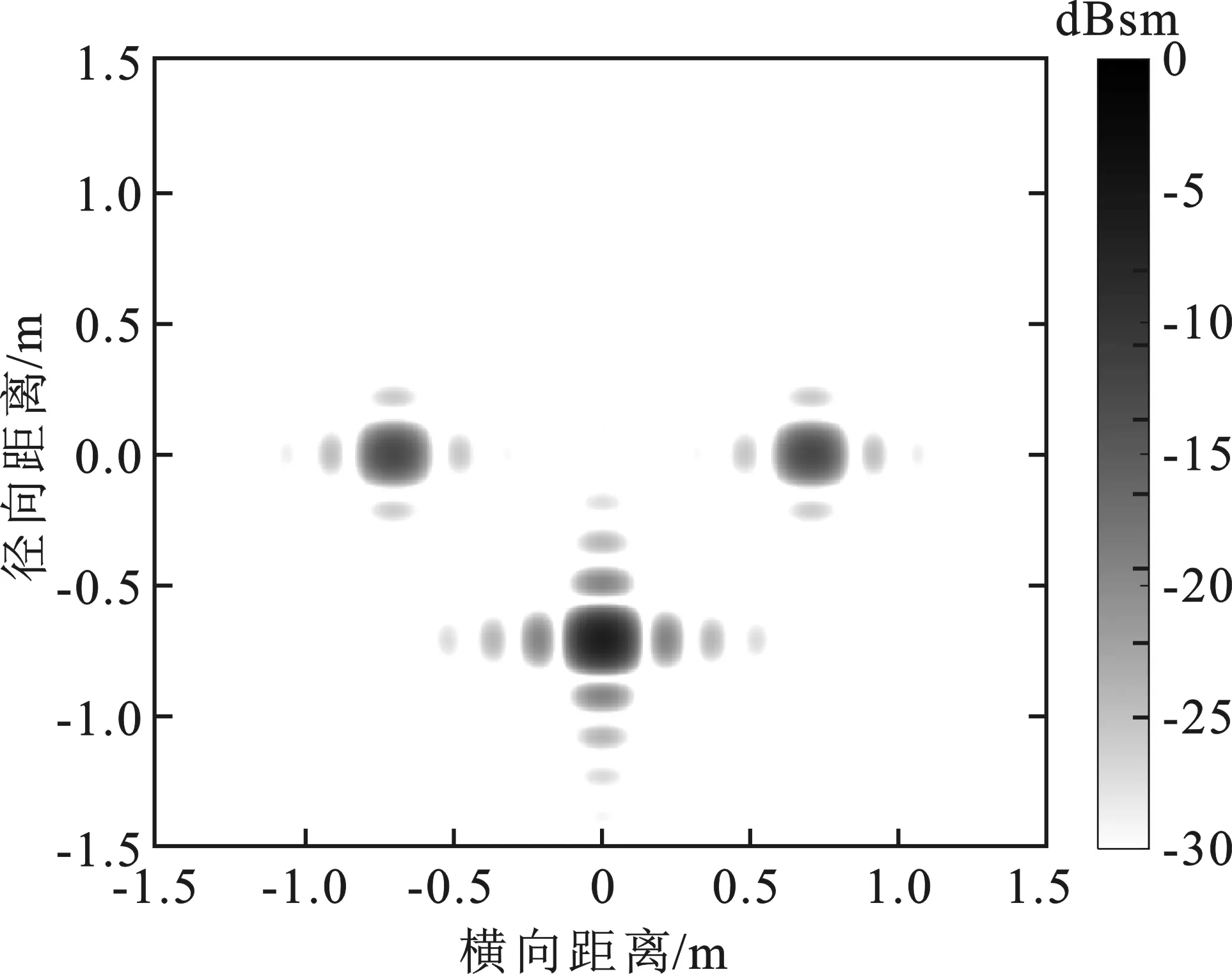
(a) YUN方法

圆柱体的几何模型和雷达截面积曲线如图3所示，尺寸为2 m×1 m×1 m。散射中心提取条件为：俯仰角90°、方位角0°～180°(1°间隔)、垂直-垂直极化、中心频率10 GHz，ISAR空间三个方向的长度均为5 m，采样点数均为128，计算ISAR像的带宽为2 GHz，两个角宽度均为12°，CLEAN算法的相对阈值为30dB。以仿真的雷达截面积为参考基准，BHALLA方法和YUN方法散射中心重建的RCS均方根误差为6.67 dB和5.63 dB，而本文方法的均方根误差为1.64 dB。从图3(b)中可看出，在方位角0°、90°和180°附近，圆柱下底面、单曲面和上底面的镜面反射为主要贡献，BHALLA方法、YUN方法和本文方法重建的雷达截面积均吻合得较好。但随着方位角逐渐偏离垂直镜面方向，曲边缘绕射成为主要贡献，BHALLA方法和YUN方法重建的雷达截面积存在明显偏差。

(a)几何模型

YUN方法和本文方法在方位角135°下的散射中心模型重建的ISAR像如图4所示，两幅ISAR像均能准确反映曲边缘散射中心的位置。YUN方法重建的ISAR像中曲边缘绕射强度分别为-26.05 dBsm、-32.04 dBsm和-32.25 dBsm，而本文方法重建的ISAR像中对应曲边缘绕射强度为-22.19 dBsm、-33.31 dBsm和-41.65 dBsm，本文结果更符合圆柱体的曲边缘绕射机理。RCS曲线及ISAR像综合对比结果表明，本文方法提取的散射中心能较好地描述圆柱体曲边缘的散射贡献。

(a) YUN方法

球头锥的几何模型和雷达截面积曲线如图5所示，尺寸为2.7 m×1 m×1 m。散射中心提取条件为：俯仰角90°、方位角0°～180°(1°间隔)、垂直-垂直极化、中心频率10 GHz，ISAR空间三个方向的长度均为 6 m，采样点数均为128，计算ISAR像的带宽为2 GHz，两个角宽度均为12°，CLEAN算法的相对阈值为 30 dB。以仿真的雷达截面积为参考基准，BHALLA方法和YUN方法重建的雷达截面积均方根误差为 5.66 dB 和4.09 dB，而本文方法的均方根误差为1.68 dB。从图5(b)中可看出，在方位角90°～170°之间，球头锥底面曲边缘绕射为主要贡献，BHALLA方法和YUN方法重建的RCS存在明显偏差。

(a) 几何模型

(a) YUN方法

YUN方法和本文方法在方位角135°下的散射中心模型重建的ISAR像如图6所示。两幅ISAR像均能准确反映曲边缘散射中心的位置。YUN方法重建的ISAR像中曲边缘绕射强度分别为-27.50 dBsm和-31.96 dBsm，而本文方法重建的ISAR像中对应曲边缘绕射强度为-22.37 dBsm和-31.99 dBsm，本文结果更符合球头锥的曲边缘绕射机理。雷达截面积曲线及ISAR像综合对比结果表明，本文方法提取的散射中心能较好地描述球头锥曲边缘的散射贡献。

(a) 几何模型

带翼组合体的几何模型和雷达截面积曲线如图7所示，尺寸为4.2 m×1.6 m×1.6 m。散射中心提取条件为：俯仰角为90°、方位角0°～180°(1°间隔)、垂直-垂直极化、中心频率10 GHz，ISAR空间3个方向的长度均为9 m，采样点数均为192，计算ISAR像的带宽为3 GHz，两个角宽度均为18°，CLEAN算法的相对阈值为30 dB。以仿真的雷达截面积为参考基准，BHALLA方法和YUN方法重建的雷达截面积均方根误差为4.33 dB和2.76 dB，而本文方法的均方根误差为1.43 dB。从图7(b)中可看出，在方位角90°～170°之间，尤其是140°～160°之间，带翼组合体的尾翼和底面曲边缘绕射为主要贡献，BHALLA方法和YUN方法重建的雷达截面积存在明显偏差。

YUN方法和本文方法在方位角135°下的散射中心模型重建的ISAR像如图8所示，两幅ISAR像均能准确反映尾翼和曲边缘散射中心的位置。YUN方法重建的ISAR像中尾翼和曲边缘绕射强度分别为-9.96 dBsm、-29.33 dBsm和-31.80 dBsm，而本文方法重建的ISAR像中对应边缘绕射强度为-8.25 dBsm、-23.56 dBsm和-35.84 dBsm，本文结果更符合带翼组合体的边缘绕射机理。雷达截面积曲线及ISAR像综合对比结果表明，本文方法提取的散射中心能较好地描述带翼组合体边缘的散射贡献。

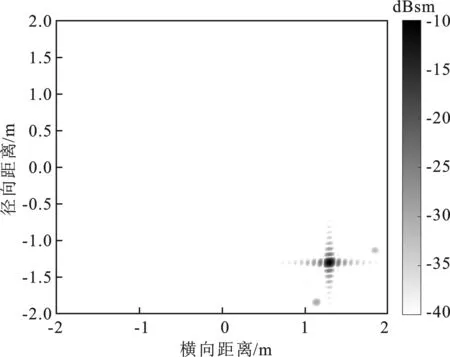
(a) YUN方法

针对四类目标，以仿真的雷达截面积为参考基准，BHALLA方法、YUN方法和本文方法提取的三维散射中心重建的雷达截面积均方根误差如表1所示。从表1中可看出，与BHALLA方法和YUN方法相比，本文方法散射中心重建的四类目标雷达截面积的均方根误差均显著减小。四类目标散射中心重建的与仿真的雷达截面积曲线及ISAR像综合对比结果表明，本文提出的用于三维散射中心建模的边缘绕射修正方法可以更准确地表达目标的电磁散射特性，验证了本文方法的有效性。

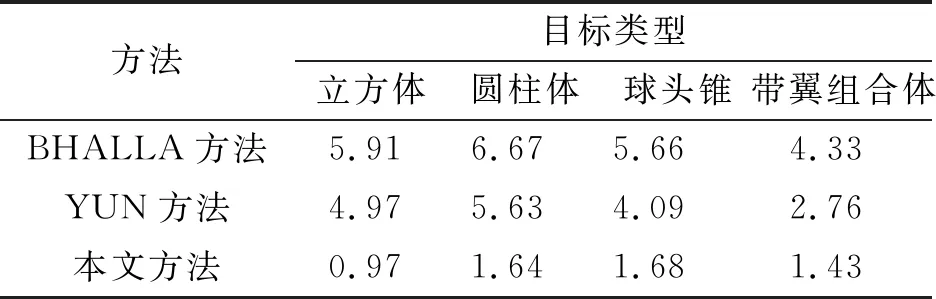
表1 BHALLA方法、YUN方法和本文方法散射中心重建的RCS均方根误差 dB

4 结束语

笔者提出了一种针对基于SBR技术的三维散射中心建模的边缘绕射修正方法。结合IDRTI技术和EEC方法，推导了考虑边缘绕射修正的三维ISAR像计算公式。在生成的ISAR像基础上，结合CLEAN算法，实现了目标的三维散射中心快速建模。针对立方体、圆柱体、球头锥和带翼组合体四类导体目标，以仿真的雷达截面积为参考基准，与BHALLA方法和YUN方法对比表明，基于该方法提取的散射中心模型重建的雷达截面积均方根误差显著减小。四类目标散射中心重建的与仿真的雷达截面积曲线及ISAR像综合对比结果表明，本文方法能够有效提高三维散射中心的提取精度，尤其对边缘绕射影响较大的目标来说，可以实现更准确的电磁散射特性表达。