广角SAR各向异性散射目标分离成像

2021-04-30常贵清池琛琛

西安电子科技大学学报 2021年2期

王昕，常贵清，池琛琛

(南京邮电大学通信与信息工程学院，江苏南京 210009)

作为一种先进的遥感系统，合成孔径雷达(SAR)[1]在过去的几十年中得到了广泛的应用。然而，线性航迹合成孔径雷达系统的方位向分辨率受限于观测角度，无法进一步提升。因此，近年来提出了广角观测[2-4]的概念，可以用于构造更大的观测角度范围。该系统可以有效地提高方位向分辨率，对后续目标分类、识别和定位具有重要意义。

然而，在广角观测[5-6]条件下，大部分物体的散射并不持久。物体的几何形状、阴影和相干闪烁可能会导致雷达的反射率与方位角[7]相关。此时，直接利用传统的成像算法重建图像会导致分辨率下降，产生的相干斑也可能会覆盖目标的相关散射特性[8]，这对合成孔径雷达图像的解析和目标识别是不利的。

众所周知，各向异性散射物体的反射在较小的数据观测范围内是稳定的[9]。因此，可以采用子孔径[10-11]方法，将整个观测范围划分为几个较小的孔径，进行广角合成孔径雷达数据的成像处理。根据视频合成孔径雷达[12-13]的方法，可以得到一组位置和方位观测角度相关的低分辨率图像。然而，单幅图像的反射信息通常是不够的。为此，有专家提出广义似然比检验(GLRT)方法[14-15]，该方法保留了占主要散射能量的子孔径贡献，经过广义似然比检验处理后，合成孔径雷达图像可解译性有所提高。上述算法都进行了子孔径的分解处理，但是没有完全利用各向同性散射目标在整个孔径观测期间的反射能量，因此重建图像的方位向分辨率仅取决于子孔径分割间隔。为提高图像分辨率，一些文献提出了正则化约束[16]方法和非线性锐化技术[17-18]。但这些方法没有充分利用散射信息，致使重建结果不理想。据悉，贝叶斯反演[19]、近似消息传递[20]和超完备字典方法[21-22]也被应用在广角合成孔径雷达成像中。在贝叶斯反演方法中，目标雷达反射率是动态变化的，可以采用动态贝叶斯压缩感知算法求解。但是，其计算复杂度较高，运算量较大。

此外，在雷达系统中，各向同性散射和各向异性散射目标的反射数据是混合接收的。由于它们的散射特性不同，需要设计的成像处理滤波器也是不同的。考虑上述原因，将两者的回波进行分离成像处理更有利于提升图像质量。但在密集场景下，这是非常困难的。另外，某些观测角度下的强反射信息会掩盖其他采集区间内的弱反射信息，从而降低图像的可解译性。为解决以上问题，笔者提出了一种基于稀疏的方法，可以对单通道的广角合成孔径雷达信号同时实现分离和成像。其中，子孔径成像后散射特性估计信息[23]被用作反馈来帮助制定雷达投影算子。稀疏约束常被用于下采样下的逆成像中[24-25]，笔者主要用它来促进合成孔径雷达数据的分离。文中算法重建图像分辨率不仅由子孔径数据采集间隔的决定，而且还由散射特性决定。此外，生成图像的可解译性也得到了改善，为后续的目标检测和识别操作提供了依据。

1 各向异性散射信号模型

只考虑雷达截面积(RCS)随方位角变化较大的各向异性散射目标。假设雷达系统发射一个调频斜率为kr和载频为fc的线性调频信号，则接收回波可以表示为

(1)

式中，τ和t分别表示距离向时间和方位向时间，函数wr(·)和wa(·)分别表示距离向和方位向包络线，σ(xa，ya，t)是位于(xa，ya)处目标的可变散射振幅信息，c是光速。R(t)表示在任意方位向时间t下，目标到雷达平台的瞬时倾斜距离。由于各向异性散射目标的σ(xa，ya，t)随方位角的变化而变化时，经匹配滤波处理后，导出的脉冲响应函数(IPR)变为σ(xa，ya，θ)和二维正弦函数的卷积，这样可能会导致主瓣带宽扩展，旁瓣的幅度增加。在这种情况下，很难提取目标的真实外观，因此需要设计新的成像处理方法。

2 各向异性散射目标的分离与成像

为了构建高聚焦质量的各向异性目标图像，在成像过程中需要考虑不同的散射特性。雷达散射截面的振幅信息是随空间和时间变化的，理想的广角合成孔径雷达数据成像处理需要一组不同长度和加权参数的匹配滤波器。此外，考虑到各向同性和各向异性散射目标的反射回波需要各自设计不同的成像滤波器，笔者提出将混合接收回波数据进行分离成像处理。

首先，构建联合雷达系统矩阵F=[Fp，Fd]，其中矩阵Fp∈CNd×NI，矩阵Fd∈CNd×NI，被称为持久性和非持久性散射目标的雷达投影算子。经距离压缩后，雷达回波数据可以表示为

(2)

其中，S∈CNd×1，是叠加接收到合成孔径雷达数据后得到的列向量。

其次，在联合雷达系统矩阵F=[Fp，Fd]中，通过对fp和fd中第i个元素的目标的合成孔径雷达系统函数进行叠加，得到Fp和Fd的第i列向量。此外，Nd和NI是指合成孔径雷达数据的长度和图像，下标p和d是指各向同性和异性目标，n0表示噪声矢量。

通常，Fp的解析表达式可以根据雷达系统参数推导出，但Fd却很难直接得到。由式(1)可以看出，方位向散射特性的影响可以看成对接收雷达数据的加权。因此投影矩阵Fd可以表示为

Fd≈FpA，

(3)

其中，A=diag{Ai}，是一个由脉冲响应函数的附加加权信息组成的对角线矩阵(该信息由各向异性散射行为引入)。由于散射特性的不同，各向同性和各向异性散射目标的雷达回波数据与系统矩阵Fp和Fd的相干性关系不同，进而可以通过在式(2)的求解中使用稀疏范数约束来实现分离。因此，建立以下优化函数：

(4)

在式(4)的迭代计算中，使用了相干加法，这意味着由被照亮目标的真实散射间隔决定重构的脉冲响应函数分辨率。另外，利用稀疏约束可以抑制噪声和旁瓣，有利于提高图像的分辨率。经过迭代计算，最终得到两幅独立的图像。

3 迭代求解

在精确地给定被照目标散射特性的情况下，可通过迭代计算求出式(4)中优化问题的解。可以利用雷达截面积估计方法来构建各向异性散射目标的雷达系统函数。但估计误差不可避免地会影响数据分离的性能，特别是当各向异性目标的散射能量很低时影响尤为明显。为了解决这个问题，笔者提出了一种预分离方法，通过该方法可以得到求解所需的初始化参数。

品读一方面要求学生把课文中的意境和情感通过抑扬顿挫的美读、赏读表达出来，达到熟读成诵的地步，最终实现课文语言的内化。另一方面，在品读中学生和文本之间要达到情感的交流、思维的碰撞。在读的基础上，学生要品出自己的味，品出自己的情，还品出自己的不同见解……这时的读已经不单纯是对课文语言的忠实再现了，而是能够表达自己情感与理解的“二度创作”了，达到“你中有我，我中有你”的读书最高境界。

3.1 预分离

经子孔径分解后，可以提供一组用于预分离过程的图像，表示为

SI=[HI1(fp+fd1)，HI2(fp+fd2)，…，HIK(fp+fdK)]+nI，

(5)

其中，SI=[SI1，SI2，…，SIK]，矩阵HIi∈CNI×NI，被称为逆成像算子，下标i表示第i个子孔径，K为子孔径个数；列向量fdi∈CNI×1，表示非持久性目标在子孔径观测区间内的场信息；nI表示图像的噪声矢量。

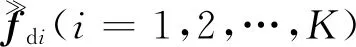
(6)

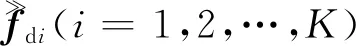
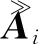
3.2 迭代计算

式(5)中的优化问题有两个未知参数。在表示f=[fp，fd]T并代入lp范数[17]的近似值后，可以将式(4)的求解过程简化为

(7)

其中，ε≥0，是一个小的正常数。为了简化求解过程，使用了一个常见的尺度参数λ，而不是限制fp和fd的稀疏特性。计算式(7)中F的实部和虚部的梯度，基于黑塞矩阵近似，可以得到如下迭代公式：

(8)

(9)

(10)

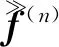
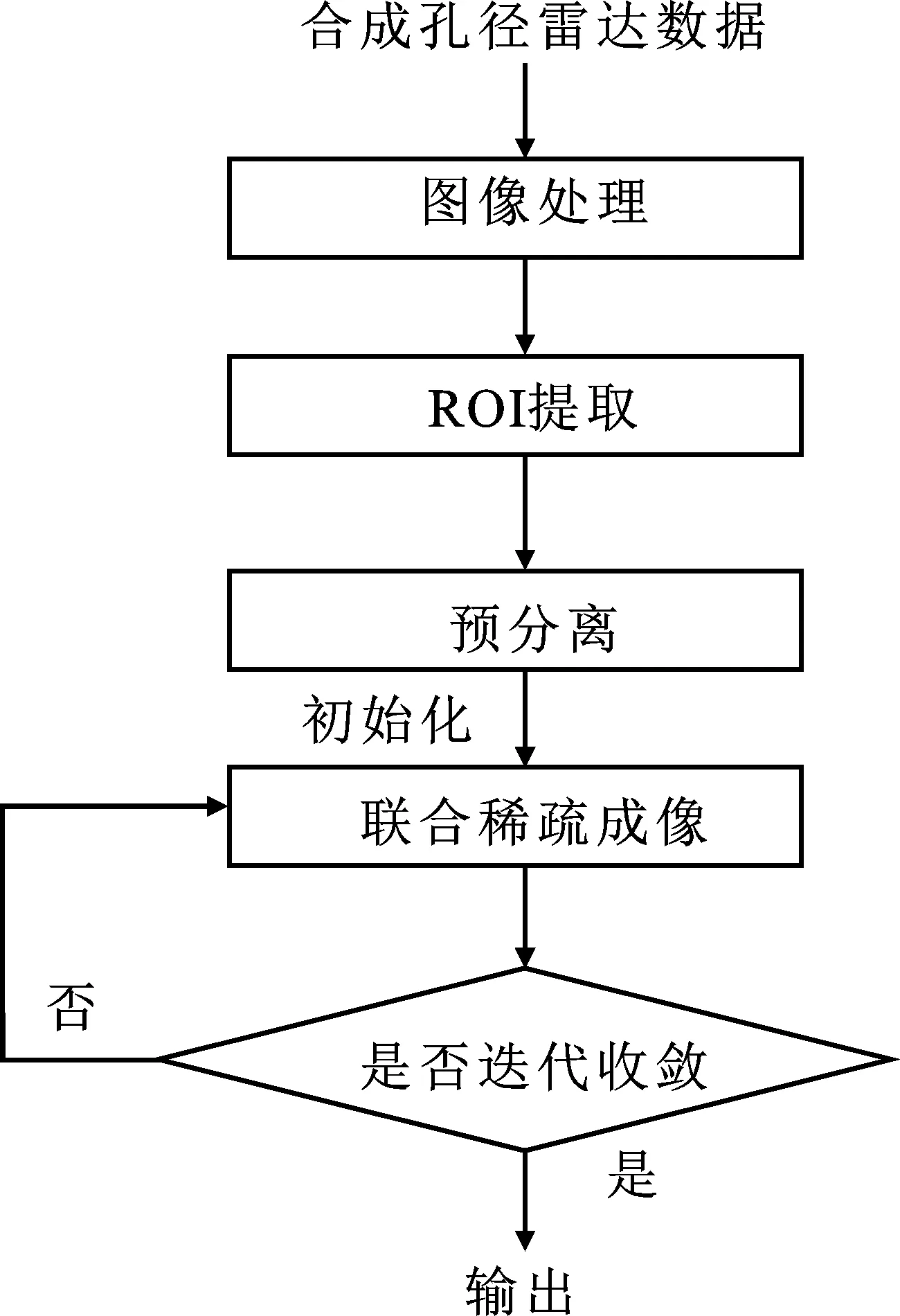
图1 联合稀疏成像处理流程图

4 仿真

本节将进行数值模拟实验来验证笔者提出算法的有效性。仿真参数如表1所示。

表1 仿真参数

在第1次仿真中，模拟了3个散射中心不变的各向异性目标和1个各向同性目标。图2(a)和(b)分别描述了模拟点的几何关系和雷达截面积函数。经过反投影处理后重建的图像如图2(c)所示，矩形框和圆形框分别表示各向同性和各向异性目标的位置。从图2(c)可以看出，由于各向异性散射行为，3个各向异性点的脉冲响应函数主瓣宽度增大。然后，划分整个孔径，得到两个子孔径(角度分别为90°和270°)，其低分辨率图像如图3(a)和(b)所示。在第2子孔径中，没有收到来自各向异性目标的反射能量，因此仅出现了一个各向同性目标。图3(c)和(d)给出了两个子孔径数据的预分离结果，其中提取了来自两个非持久性点的大部分能量。在稀疏成像之后，各向异性目标的成像如图3(e)和(f)所示。从图中可以看出，各向同性散射点和各向异性散射点都是集中的。

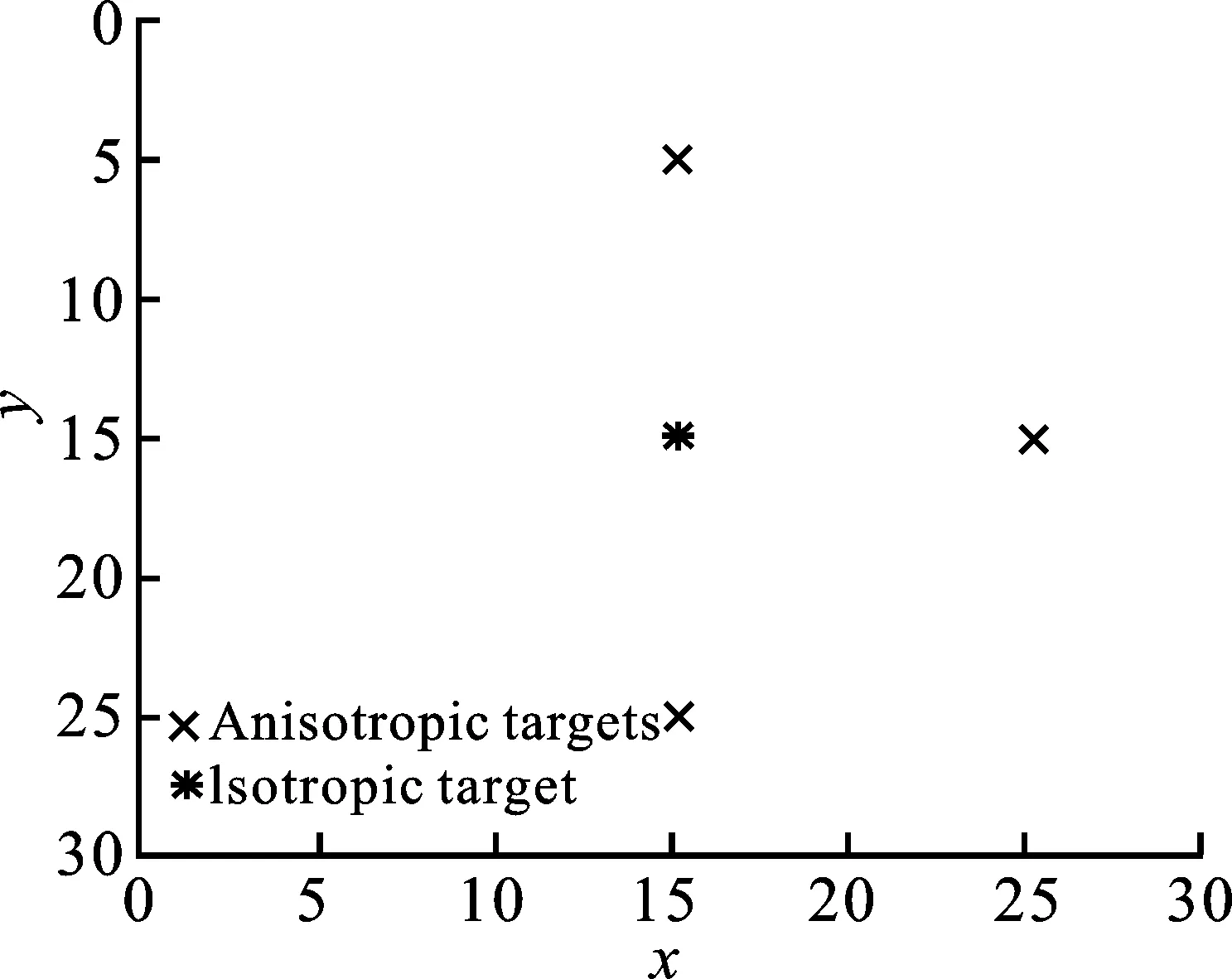
(a) 模拟点的几何关系

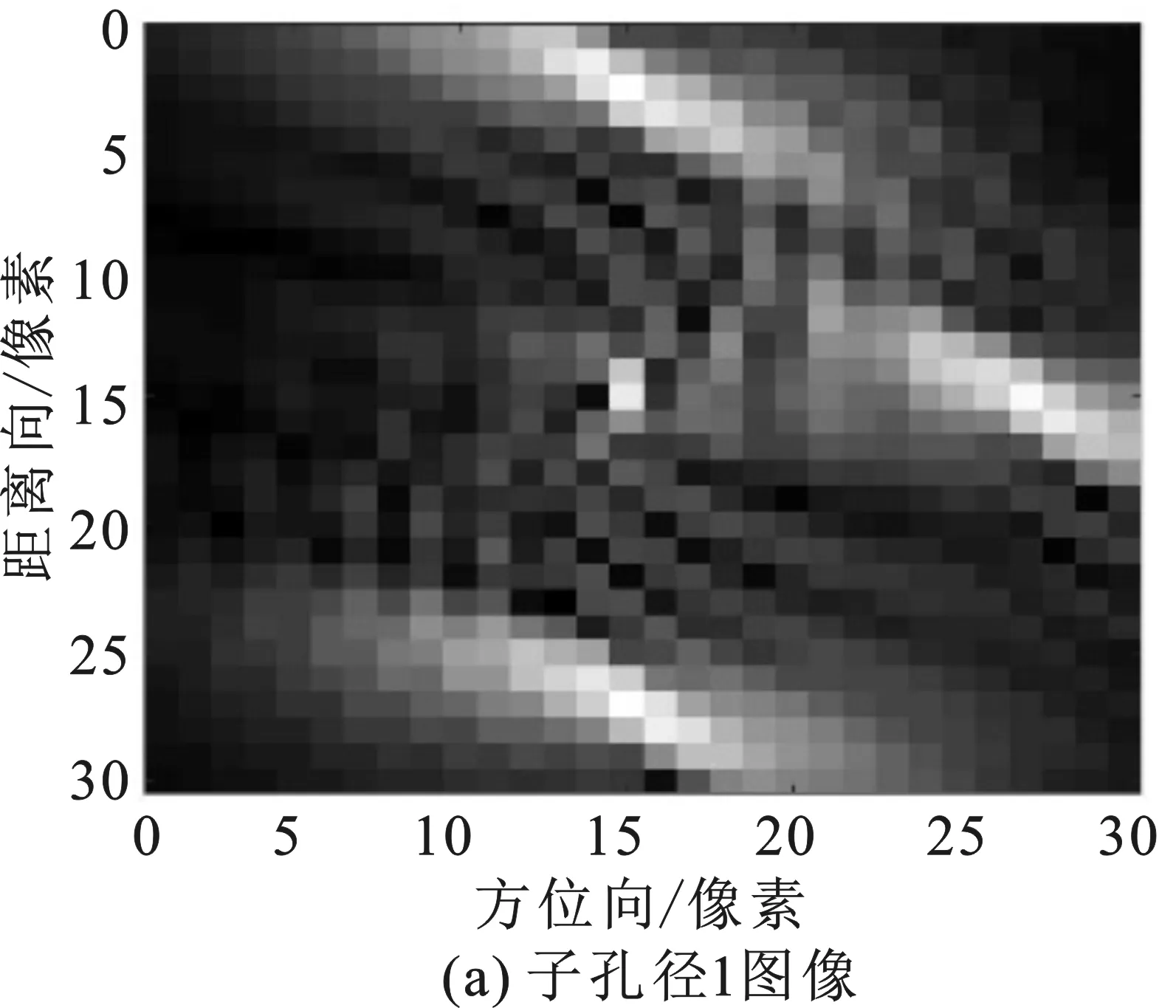
图3 子孔径图像和预分离结果(注：2个各向异性散射目标的散射中心不变)

在第2个仿真中，设计了一个散射中心可变的圆形目标和27个散射中心不变的点目标。在成像处理过程中，得到的全孔径图像如图4(b)所示。划分全孔径，得到4个子孔径(方位角为45°、135°、225°、315°)，如图5(a)～(d)所示。

(a) 仿真中的点

从图4(b)可以看出，图像被涂抹，被照亮目标的真实外观无法显示。由于散射特性的不同，从子孔径得到的子图像是不同的。

图5(e)～(h)分别给出了4个子孔径的预分离结果。对各向异性目标的雷达分离数据采用基于联合稀疏的方法进行处理。

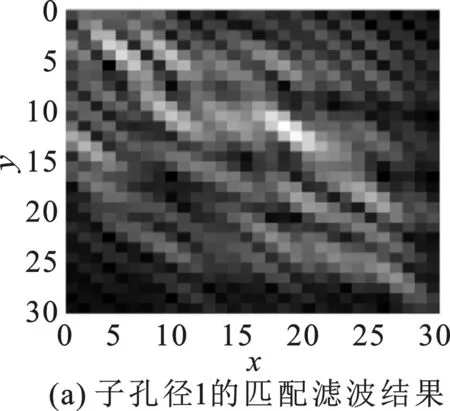
图5 子孔径成像和分离结果

然后，依次进行散射中心提取和雷达截面积估计操作，并更新雷达系统操作。最终，各向异性目标的生成图像如图6(c)所示。从图6中可以看出，所提算法实现了各向异性目标的分离和去模糊。

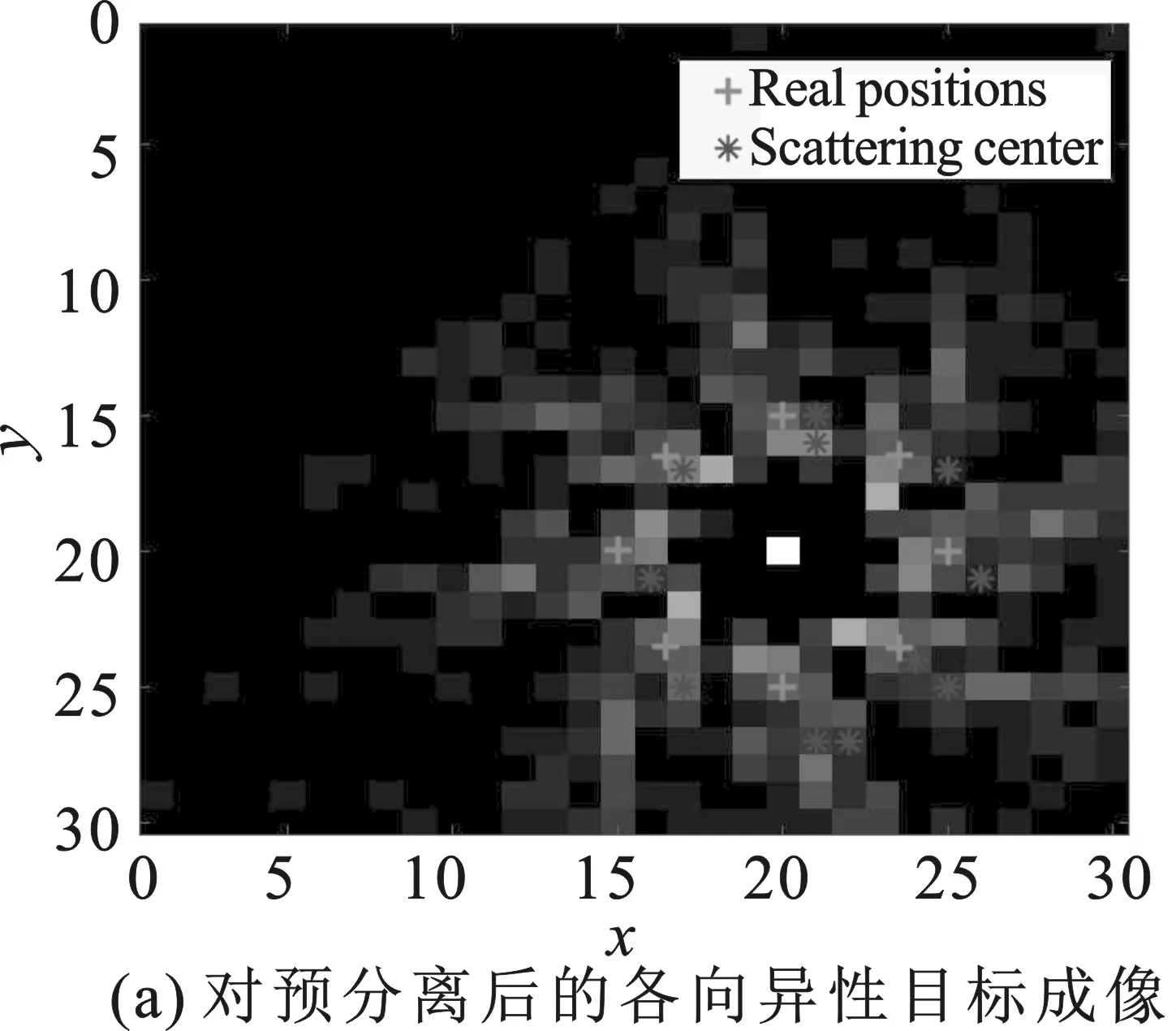
图6 利用文中方法得到的成像结果

在第3次仿真中，对空军研究实验室(AFRL)的Backhoe数据分别进行相干匹配滤波、广义似然比检验(GLRT)和稀疏处理的操作。反铲数据观测角度宽度为110°，仰角分别为0°和30°。数据中的目标大多是非持久性散射。因此，通过相干和非相干处理得到的图像并不令人满意，如图7所示。方位角为90°～110°时的强反射能量掩盖了其他弱散射目标，从而影响重建图像的解析。

在基于稀疏分布的处理中，通过子孔径划分操作来提供一组图像来进行预分离。如文献[13]和文献[16]所述，大多数非持久性散射目标在较小的观测间隔内都能保持反射。将整个孔径分为19个间隔，每个区间的方位角响应中心为0°，5°，…，90°，观测视角宽度为20°。经过反投影处理，可以得到19幅不同方位角的低分辨率图像。由于数据中大多数被照射目标的散射是非平稳的，此处不再进行预分离操作。随后，分析任意两幅子图像之间的相关性，并应用简单的聚类算法来帮助找到好的子孔径分解方案。基于以上研究结果和数值模拟经验，最终将广角观测孔径划分为3个子孔径。根据式(7)，将3个子图像相干相加，帮助生成初始化的图像，其中，图7(a)～(c)和图8(a)～(c)分别给出了不同方位角对应的成像结果。图7(f)和图8(f)分别给出了仰角为0°和30°的最终生成图像。从图7(e)和图8(e)也可以看出，用广义似然比检验方法得到的图像的分辨率受到子孔径观测间隔的影响，而被照射目标的实际散射间隔可能会超过我们划分的间隔。相比之下，利用全孔径数据和基于稀疏处理的实际散射行为，提高了重建图像的分辨率和可解译性。