一种改进的泊松点过程概率多假设跟踪方法

张逸宸，水鹏朗

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

雷达系统需要实时准确地跟踪“湮没”于杂波中，往往不能被完美检测到的多个目标[1]。多目标跟踪算法的核心是关联问题[2，17-20]，关联解决了目标漏检和虚警带来的不确定性。早期雷达分辨率低，目标尺寸远小于雷达分辨单元大小，目标可以被视为不会扩展的点目标，所以传统跟踪方法诸如联合概率数据关联[3]和多假设跟踪[2]都假设目标和量测“一一对应”，即一个目标最多产生一个量测，一个量测最多与一个目标相关联，并从穷举出的量测与目标间所有可能的关联中估计出最优关联。但由于关联假设间相互依赖，一个量测与目标的关联会影响其他量测与该目标的关联，穷举联合假设是一个无法在多项式时间内求解的NP-hard(Non-deterministic Polynomial hard)问题，爆炸增加的计算量制约了雷达跟踪多个目标的能力，如何降低多目标跟踪算法的关联复杂度，是雷达领域关注的焦点。

在高分辨雷达系统中，目标尺寸往往远大于分辨单元，一个目标可能产生多个不连通的量测；这些量测点可能无法凝聚成一个量测点[5]，坚持“一一对应”的假设准则反而会造成一定性能损失[6]。概率多假设跟踪(Probabilistic Multi-Hypothesis Tracker，PMHT)[7-10]默认一个目标可以产生多个量测，每个量测点是对目标和杂波组成的混合过程的一次独立实现，量测关联假设相互独立，因此，PMHT的关联复杂度仅随目标数目线性增加。传统PMHT方法采用伯努利点过程(Binomial Point Process，BPP)为量测建模，将量测与航迹的关联状况视为缺失信息，利用EM算法(Expectation Maximisation algorithm)迭代估计目标状态。但由于伯努利点过程的负相关性质导致独立目标的混合概率不独立，每次迭代中需要更新所有目标状态，已稳定收敛的目标被重复迭代导致大量算力的浪费，致使实际应用中算法运行时间与传统方法相当[6]。文献[8]采用独立的受伽马分布调制的混合概率减少了目标平均迭代次数，但是复杂的计算过程和严苛的参数初始化要求限制了该方法的应用。笔者采用泊松点过程(Poisson Point Process，PPP)[10]为量测模型，选择泊松分布参数作为目标和杂波的混合概率，利用泊松分布的独立性只迭代未收敛的目标，降低了算法运算复杂度。

PMHT算法默认一个目标可以产生多个量测，大量虚警也被当做目标量测加入关联滤波[5]，仅利用空间位置信息无法区分量测的真实来源，影响了航迹质量。额外利用目标回波特征信息，如多普勒、目标RCS信息，可以在不增加运算量的同时提升跟踪算法精度[11-12]。使用回波多普勒量测作为目标特征辅助跟踪，利用虚警和目标量测在多普勒域内的区别辨识量测来源，解决了原有方法易受虚警影响的问题，提升了跟踪精度。此外，PMHT需要已知目标数量和状态等先验信息，在实际雷达系统中需要配套航迹管理方法以估计目标数目。文献[11]利用Hough变换起始和移除航迹，实现航迹管理；文献[7]过估计目标数目，实现了航迹起始和维持的统一；文献[6]指出上述方法的效率低的缺点。笔者提出了一套与PMHT适配的航迹管理方法，与杂波关联的量测被用于起始新生航迹，混合概率被用于评价航迹质量，依据航迹质量判断是否维持和输出显示航迹。

1 概率多假设跟踪方法

(1)

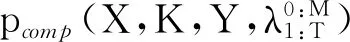
(2)

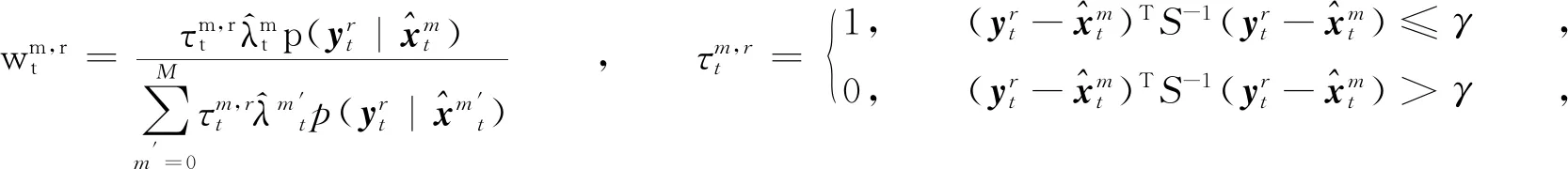
(3)

M步通过最大化辅助方程得到新的估计，每次迭代中，目标和杂波的混合概率以关联权重更新，即

(4)

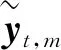
(5)

式中，Q是系统量测噪声。在迭代中如果目标的辅助方程收敛，则固定目标的状态和关联权重，实际系统中往往基于每帧最长处理时间设置最多迭代次数限制。具体算法如下。

算法1泊松点过程概率多假设跟踪。

② 辅助方程收敛的目标固定目标状态、混合概率和关联权重不变。

④ 使用卡尔曼滤波器更新目标状态估计。

⑤ 迭代步骤②～④，直至所有目标辅助方程收敛，输出目标状态。

2 量测方程

PMHT假定一个目标可以产生多个量测，不需要输入凝聚后的数据[8]，未凝聚的数据包含了更多的目标信息，但需要扩大关联波门范围以容纳目标在距离维度的扩展。更多的虚警和其他目标的量测将出现在关联波门内，传统方法仅利用量测的位置信息并不能准确区分量测的来源，在目标密集区域或虚警较高的场景下跟踪性能不佳[5]。额外利用目标回波的多普勒信息可以提升跟踪性能，依据目标与目标、目标与杂波在径向速度上的不同可以区分量测来源；此外，由于多普勒信息体现目标径向速度，更多的信息的加入提升了滤波精度。笔者将回波的多普勒信息作为目标特征，重构包含了多普勒信息的量测方程，采用转换量测的方法将非线性的量测方程转换成伪线性模式。考虑二维情况，转换后的量测方程可以表示为

(6)

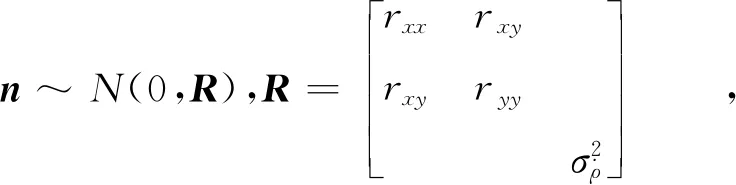
3 航迹质量与跟踪流程

航迹质量作为航迹可信度的评价指标，反映了航迹与量测点的关联状况，是终结陈旧航迹、维持现存航迹的标准。量测点与预测点的马氏距离是传统跟踪方法中一类重要的航迹评价指标。在PMHT方法中，目标混合概率表征每帧产生量测点的个数，是航迹质量评估的有效检验统计量[8]。笔者将目标混合概率和传统方法中评价航迹常用的马氏距离融合，航迹质量由关联量测点数目和空间位置综合评估。文中使用的航迹质量如下：

(7)

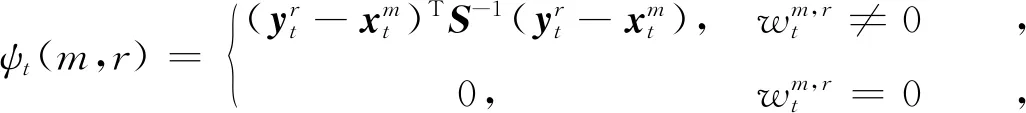
式中，S是协方差矩阵，ψt(m，r)是量测点到预测点的马氏距离。由于目标存在漏检，单帧数据不能客观评价航迹可信度，因此，结合近一段时间的航迹关联状况评估航迹质量，真实的目标产生持续的关联量测，所以具有较大的航迹质量。

跟踪流程如图1所示，量测点航迹和现存航迹输入PMHT算法关联滤波得到新时刻的航迹，随后合并相近航迹并评估航迹质量，使用航迹维持门限α和航迹显示门限β(β≥α)判断航迹是否维持，是否输出显示。通常为了防止有用的航迹过早删除，航迹维持门限α设置得较低，而航迹显示门限β设置得较高。为了避免虚假航迹的显示，利用与杂波关联的量测起始新生目标，避免重复起始现存航迹，产生的新生航迹加入现存航迹中等待下一帧滤波更新。

图1 跟踪流程

4 实验分析

采用仿真数据验证了笔者所提方法具有高跟踪精度和低运算量的特点。4.1节聚焦海面小目标跟踪问题，使用仿真的岸基搜索警戒雷达数据[13-15]，说明了笔者所提方法有效抑制了虚假航迹，提升了跟踪精度；4.2节模拟了复杂多目标跟踪场景，采用蒙特卡罗实验数值验证了笔者所提方法运算复杂度随目标数量线性增加的特点。

4.1 海面小目标跟踪

实验中仿真了X波段岸基搜索警戒雷达的数据，分辨率是3 m，脉冲重复频率为2 000 Hz，雷达架设在原点，盲距为1 500 m，半功率波束宽度为1.44°，共仿真了20个波位。高分辨海杂波呈现“非高斯”“非平稳”的性质，幅度分布具有较重的拖尾，采用广义Pareto(Generalized Pareto)[16]分布，描述海杂波分布并使用其分布下最优检测器——广义似然比线性门限检测器做检测，虚警率设置为10-3。仿真中加入了5个功率起伏服从Swering1模型的小目标，平均信杂比为3 dB，检测概率分别为 0.527、0.553、0.513、0.543、0.567。

图2(a)中给出了检测后的点迹和仿真目标轨迹，图中的灰色区域是雷达探测范围，图2(b)、(c)、(d)中分别给出了JPDA方法、传统PMHT方法、文中所提基于泊松点过程的PMHT方法的跟踪航迹结果，表1给出了各种方法OSPA距离和运行时间。从图2和表1中可以看出，传统的PMHT易受虚警点干扰，航迹常常被附近的虚警点拉偏，跟踪质量差；JPDA虽然能稳定跟踪所有主要目标，但产生大量的虚假短航迹且算法运行时间相对较长；文中所提方法额外利用了回波多普勒信息，增强了区分量测来源的能力，OSPA距离小，说明航迹接近于真实目标状态，不产生虚假航迹，跟踪质量高。

表1 平均OSPA距离及运行时间

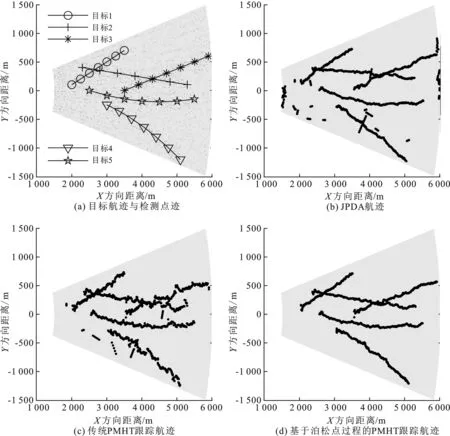
图2 跟踪结果

4.2 运算复杂度分析

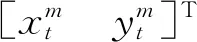
(8)

仿真目标在空间中沿直线周期性往复运动，目标轨迹经常交叉或者近似交叉，比拟了多目标跟踪中的极端情况。图3给出了14个目标的一个完整运动周期，方框表示每个目标最新位置，直线拖尾则是目标在这段时间内的轨迹。

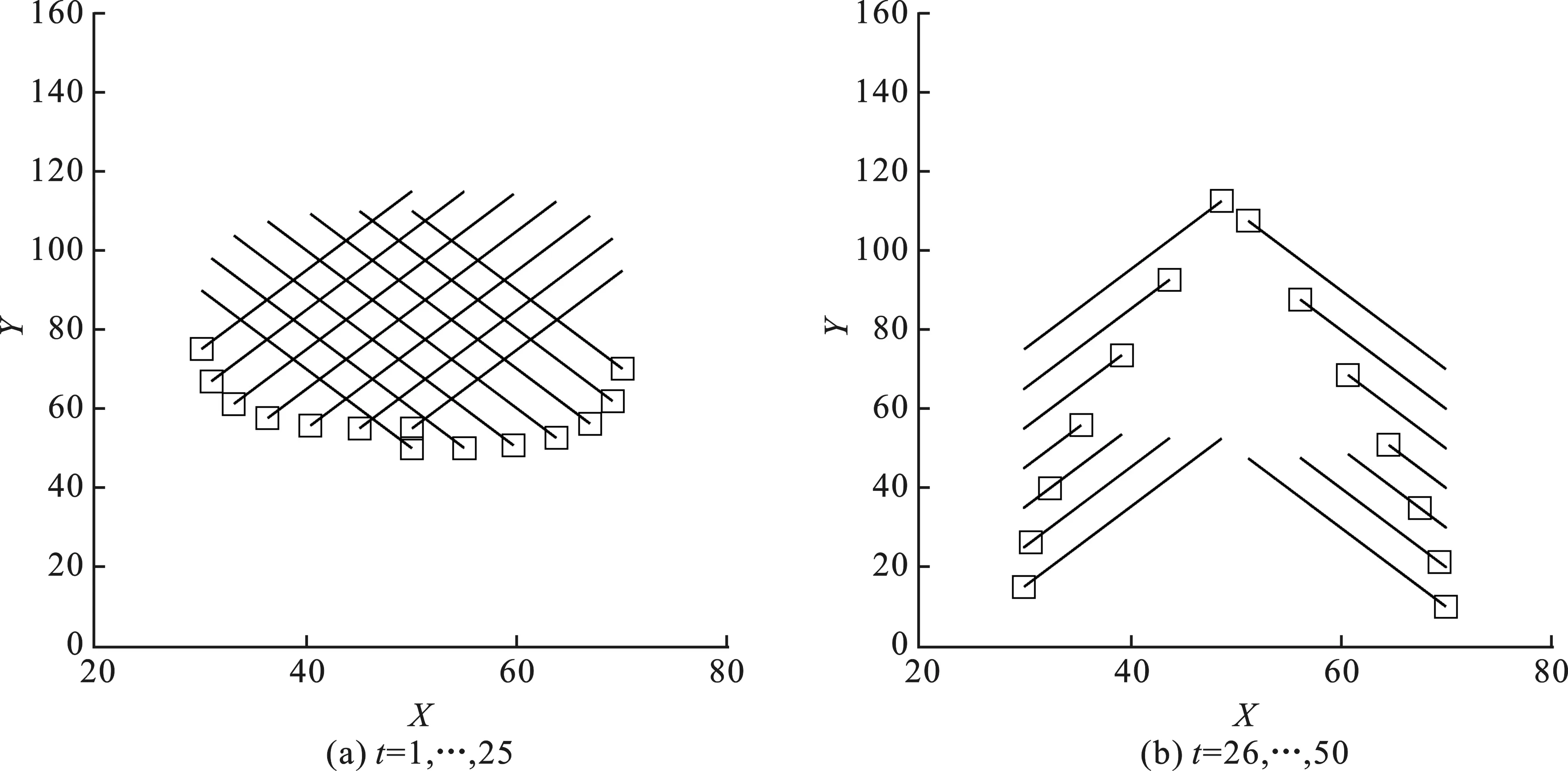
图3 仿真14个目标场景

图4给出了不同跟踪方法平均每帧运行时间与目标数目的关系，平均每帧计算时间由50 000次蒙特卡罗实验获得。从图中可以看出传统跟踪方法诸如JPDA、MHT的平均计算时间呈指数倍增加，这与联合假设的不独立性质有关。传统PMHT方法虽然关联复杂度随目标线性增加，但是需要迭代求解所有目标状态，运算时间近似与目标数目的平方有关[9]，在目标数目较少时计算时间略大于传统跟踪方法。文中所提方法由于不需要重复更新已经收敛的目标，平均迭代次数少于传统PMHT方法，运算时间随目标数量线性增加。

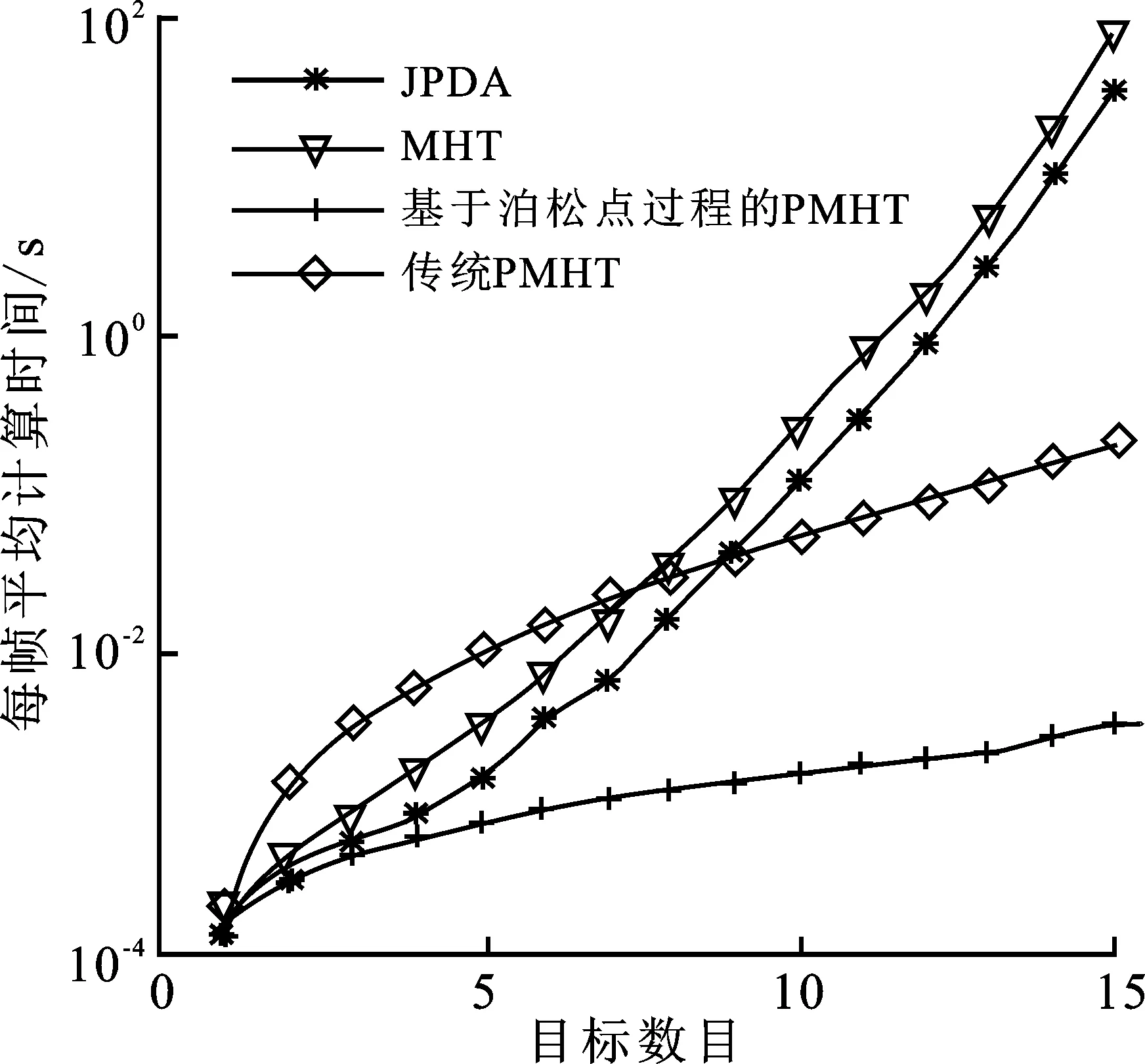
图4 算法运行时间

5 总 结

笔者提出了一种高精度、低运算复杂度的多目标跟踪算法，使用泊松点过程代替传统PMHT方法中伯努利点过程为量测建模，独立的关联假设和目标混合概率参数降低了计算量，同时引入回波多普勒信息作为目标特征辅助跟踪，抑制了虚警点对于航迹的影响，减少了虚假短航迹的产生，提高了跟踪精度。实验表明，文中所述方法运算复杂度随目标数量线性增加且跟踪精度优于传统方法。