基于自适应权重的立体匹配优化算法
2021-04-29文斌,朱晗
文 斌,朱 晗
(三峡大学电气与新能源学院,湖北宜昌 443000)
0 概述
立体匹配是指通过双摄像头中的二维场景,利用视差匹配获取三维场景的深度信息,被广泛地应用于移动机器人技术、3D 建模技术、航空航天[1]等领域,是双目立体视觉的重点和难点,立体匹配的精确度决定了立体视觉的最终效果。因此,研究更加高效、精确的立体匹配算法具有重要意义。
目前,立体匹配主要分为全局匹配和局部匹配两大类[2-3],文献[4]根据双目立体匹配算法的特点进行归纳总结,将立体匹配算法分为匹配代价计算、代价聚合、视差计算和视差优化4 个部分。全局匹配是利用图像的全局约束信息构建全局能量函数,通过优化算法使得全局能量函数最小从而构建稠密视差图。虽然全局匹配精确度较高,但是全局匹配存在运算复杂、能量函数不易构建等问题。而对于局部匹配,由于其运算速度快、算法的复杂度低、能量函数易构建等优势,因此更加受到研究人员的青睐。
局部立体匹配主要是通过局部像素的代价聚合实现的,具有代表性的传统的代价聚合算法有SAD[5]、SSD[6]和NCC 归一化[7]匹配算法。SAD 和SSD 匹配算法计算量小、运算速度快,但是该算法的匹配准确度完全依赖于中心点的灰度值,并且由于其代价聚合是等价聚合,易受到低纹理区域以及视差不连续区域的干扰,产生大片的误匹配区域和视差空洞。NCC 归一化算法可以有效地降低光照对匹配的影响,但传统的NCC 算法运行较慢,且其匹配率对于SAD 算法而言没有优势。
BM 匹配算法是基于字符串搜索规则和SAD 匹配算法的代价聚合实现的,采用坏字符与好后缀的原则进行匹配[8],相对于SAD 算法,低纹理区域的匹配有了一定的完善,但对于复杂环境的视差不连续区域的匹配依旧存在较大缺陷。
立体匹配的核心思想是将特定区域内的多个像素点的相互联系归一化到一个能量函数的框架之下,将立体匹配的最优匹配问题转换成能量函数最小化问题。为构建更好的能量函数,提高匹配精度,国内外学者对立体匹配进行了研究。文献[9]提出了自适应权重的立体匹配算法,将自适应的概念引入到代价聚合中,根据Lab 颜色空间的相似性和欧式空间距离的接近性自定义代价权重,结合双边滤波器,表现出了较好的性能。文献[10]介绍了一种新颖的基于三边滤波器的ASW 方法,该方法使用了RGB 颜色空间的相似性,并将匹配代价改为灰度差异值和X方向上梯度差异值之和。文献[11]融合权重的思想,实现灰度、汉明距离、梯度三者代价的非等比例聚合,在聚合代价前加入滤波权重,以期降低立体匹配代价体积滤波计算成本。文献[12]将基于灰度空间的自适应权重算法与Census 变化融合,提高算法在实际场景的稳健性。文献[13]将权重系数的Lab 空间颜色相似性改为RGB 颜色空间相似性,以满足机器人平台实际应用中广泛使用的摄像机模式。
本文提出一种基于自适应权重的立体匹配优化算法,该算法基于自适应权重算法的核心框架,并保留了Lab 空间颜色的相似性和欧式空间距离的接近性。为使得自适应权重算法能与其他处理算法有良好的兼容性,对初始匹配代价进行修改,将RGB 颜色空间差异与高斯差分图像差异进行聚合来设置截断阈值,并选择边缘约束对遮挡部分进行视差同化。此外,为并保证自适应权重算法运行时不受窗口大小的影响,提出基于高斯差分图像判断的自适应窗口算法,以保证匹配算法的最优性能。
1 自适应权重的匹配算法
1.1 ASW 算法
自适应支撑权重(Adaptive Support Weight,ASW)立体匹配算法一种经典局部匹配算法,该算法是在SAD算法的基础上进行的改进,修改了SAD 匹配算法的匹配代价并增加了自适应权重。因此,与SAD 匹配算法不同,ASW 算法在代价聚合时是根据格式塔理论,并不是简单地将窗口内所有像素的匹配代价等价聚合,其核心思想是为窗口内每一个像素分配一个合适的权重,计算单个像素的权重,然后进行加权汇总代价。根据格式塔理论的接近性与相似性原理,距离越小,分配的权重越大,颜色越相似,其分配的权重也会更大。假设q是以p像素点为中心的窗口内的任意一点,其空间的接近性定义为:

其中,λd为距离差异系数,ΔDpq为p和q在欧式空间中的距离:
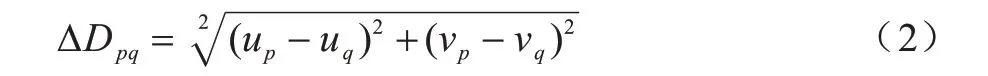
其颜色的相似性定义为:

其中,λc为颜色差异系数,ΔCpq为p和q在Lab 颜色空间中的距离:

那么,p和q之间的权重定义为:

则匹配代价E(p,)的计算公式为:

其中,是在视差范围内,像素点p、q匹配的被搜索图像中的像素点,Np是以p点为中心的窗口,e(q,)表示q点与点之间的初始匹配代价,Ic表示像素点所在颜色空间的色度值,c属于RGB 颜色空间分量,T是截断阈值。
1.2 ASW 改进算法
针对立体匹配中低纹理区域和视差不连续区域,ASW 算法的匹配效果表现一般。本文通过改进ASW 算法来优化低纹理区域和视差不连续区域的匹配。
低纹理区域和视差不连续区域的匹配问题普遍存在于立体匹配中,低纹理区域的误匹配易造成视差空洞,视差不连续区域的误匹配问题很容易造成忽略图像细节区域。因此,本文算法从初始匹配代价上着手改进,在求RGB 颜色空间分量差分和的基础上加入高斯差分图的差分值:

其中,A为RGB 颜色空间分量差分权重,B为高斯差分图差分权重,本文取A=0.1,B=0.1。ΔDOGq为像素点q和的高斯差分图像差分的绝对值:

假设是一对待匹配点,则DOGq、DOGq分别为参考图像和搜索图像的高斯差分图像[14-15]。
1.3 自适应窗口
低纹理区域的匹配问题一直是立体匹配中的难点。低纹理区域的匹配窗口选择过小,就无法得到更多的特征像素点,难以准确匹配,纹理丰富的区域匹配窗口选择过大,易造成前景膨胀效应和匹配计算复杂度过高。针对上述问题,文献[16]提出了通过测算局部灰度和视差变化来选取适当窗口的方法,但该方法效率低下,对视差初值的要求较高。文献[17]针对文献[16]中存在的问题,提出一种仅利用灰度信息确定窗口的方法,该方法解决了文献[16]中效率低下、初值敏感的问题,但该方法的计算量仍不能满足实际需求。文献[18]采用灰度信息的自适应窗口算法,根据窗口内像素灰度值的平均值选择窗口,但其算法的主要作用是用于降低运算时间,图像的误匹配率没有降低,反而略有升高。
本文提出的自适应窗口的优化匹配算法主要解决低纹理区域的匹配及降低误匹配率,而在时间上不做过多要求。该方法的原理是基于图像特征在尺度空间[15,19]的“模糊”特性。所谓尺度空间的“模糊”特性,是假设从不同的距离观察一个物体,物体上的特征并不会因为观察距离的远近而在视角中消失,只是特征变模糊,而稍弱的特征则会因为过度模糊并不能被人们所捕捉,相当于“消失“。在图像处理中,通过不同尺度的高斯函数“观察”图像,不同强度的特征点受到尺度空间变化的影响也就较小。因此,根据式(10)计算高斯差分图像:

其中,I(x,y) 为图像的灰度值,Gσ1(x,y) 和Gσ2(x,y) 分别为σ为σ1 和σ2 时的高斯函数,*为卷积符号,g1(x,y)和g2(x,y)分别为滤波后的灰度图像。
σ1、σ2 分别取0.1 和255 时的高斯函数图如图1所示。

图1 二维高斯函数图Fig.1 Two-dimensional Gaussian function diagram
对标准图像的高斯差分处理结果如图2 所示。

图2 高斯差分图像Fig.2 Gaussian difference images
以图2(a)Tsukuba 图像为例可以明显看出,图中右上角以及台灯、桌子等低纹理区域在高斯差分图像中的像素点的像素值很低,而书架、摄像机等纹理丰富区域在高斯差分图像中像素点的像素值较大。因此,根据式(11)、式(12)可以很明显地区分出区域的纹理丰富程度,对于低纹理区域:
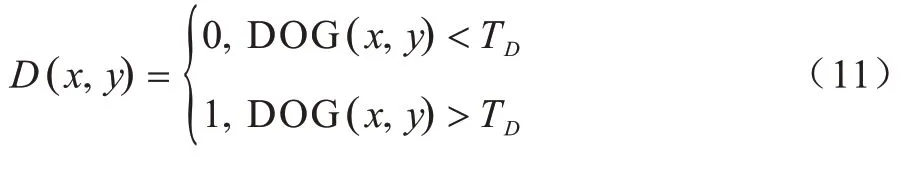

其中,D(x,y)为图像DOG(x,y) 的二值化图像,TD为阈值,统计大小为K×K窗口内大于阈值TD的像素点个数,若个数小于ε,则为低纹理区域,选择较大窗口。
基于高斯差分图像的自适应窗口算法实现简单,算法复杂度较低,能够直观地判断区域的纹理丰富性。
2 视差计算
2.1 WTA 算法
采用胜者为王(Winner-Takers-All,WTA)[20]算法计算最优视差,假设视差范围是0~n,E0,E1,…,En是在视差范围内搜索到的像素点的匹配代价,取匹配代价最小值Eσ(σ∈[0,n])所在的点作为待匹配点的最优匹配点,则该点的视差为σ。

WTA 算法示意图如图3 所示。
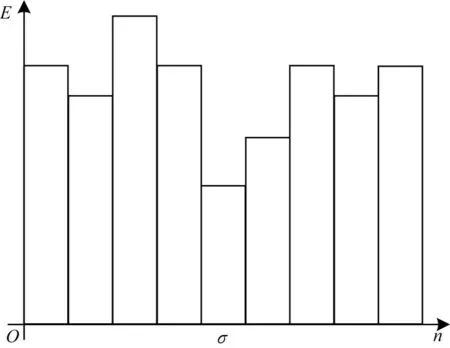
图3 WTA 算法示意图Fig.3 Schematic diagram of WTA algorithm
2.2 遮挡区域的优化
在得到初始视差图后,仍存在一些遮挡区域的误匹配点。应用左右一致性原则,找到遮挡区域的误匹配点。
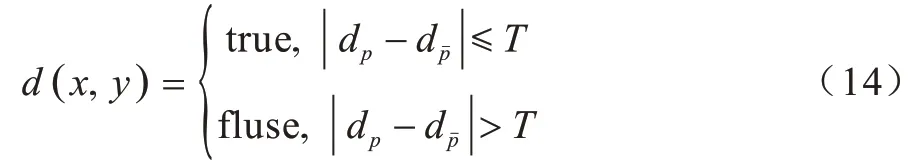
其中,点是p点的匹配点,d(x,y)为p点所在图像的视差图,dp为p点的视差值,为点的视差值。如果两点的视差差分小于等于T,则认为是正确匹配点;如果两点的视差差分大于T,则是误匹配点。
在得到遮挡区域的误匹配点后,再利用邻点法,以误匹配点为中心对4 个方向进行搜寻,找出距离误匹配点最近的正确匹配点,将最近的正确匹配点的视差值作为遮挡点的视差值。

其中,df为误匹配点的视差值,da、db、dl、dr和da-d、db-d、dl-d、dr-d分别为上下左右方向上的最近正确视差点的视差值以及最近像素距离。
3 基于边缘约束的视差聚类
对遮挡区域的误匹配点优化完成以后,视差图中在低纹理区域以及光线过亮区域仍存在大量的误匹配点,并且这些区域还存在视差空洞的问题。针对上述情况,本文引入边缘作为约束条件,分区域对边缘约束内的视差点进行聚类处理,减小误匹配点的误差,消除视差空洞。主要步骤如下:1)将边缘图像加入到视差图中;2)将边缘作为约束条件,对视差在横纵方向上进行处理;3)清除边缘;4)图像滤波;5)迭代优化。
3.1 边缘算子的选取
本文引入图像边缘对视差图进行边缘约束,选取的是Canny 算子[21],原因如下:1)Canny 算子在图像预处理阶段使用高斯滤波平滑图像,有效地去除了噪声,降低了伪边缘的识别;2)Canny 算子使用非极大值抑制技术,通过寻找像素点的局部最大值,对非极大值的像素点进行抑制,有效地剔除了大部分非边缘像素点;3)采用滞后阈值法,设置高阈值DH与低阈值DL,有效地去除了大部分噪声。
针对Canny 算子高斯滤波以及高低阈值设置,可以根据取主去次的原则,即保留主要的边缘区域,省略掉一些不重要的边缘,图像的整体大概轮廓保留即可。
在得到参考图像的边缘图像后,将边缘图像与视差图进行相加得到新的图像,本文将该图像称之为视差边缘图像。
3.2 边缘约束视差聚类
针对边缘约束区域内存在的误匹配点和视差空洞,分别从横、纵两个方向对视差点进行处理。对横轴方向上的处理如下:

在式(16)~式(19)中,先求得横轴方向上相邻边缘点约束的非边缘视差点的视差值之和sumX0,x0表示左边缘点所在的横坐标的值,countP表示相邻边缘点约束的非边缘视差点个数,dg(x,y)表示视差边缘图像,值255 表示边缘上的点的像素值,然后再根据统计的点,求得横轴方向上相邻边缘点约束的非边缘视差点视差的平均值davgX0,count表示相邻边缘点约束的非边缘视差点以及非视差空洞点的个数。
但上述方法在计算平均视差值时包含了一些离群点,这些点往往是一个视差值远小于正常值的误匹配点,导致该方向上整体视差值减小。运用式(20)消除离群点,得到正确视差:
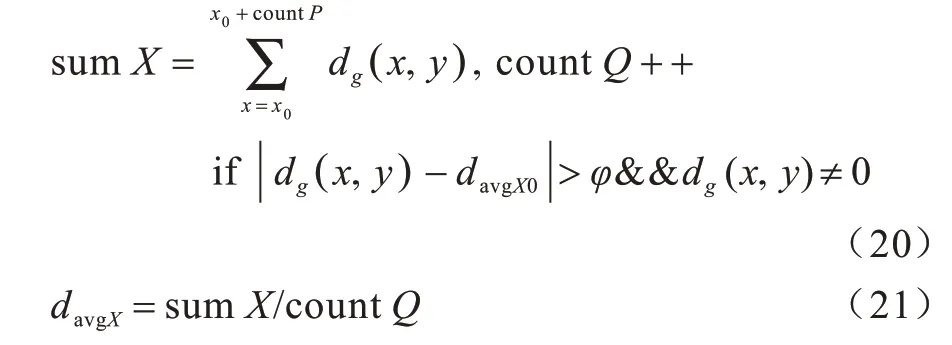
其中,sumX表示横轴方向上非异常视差点的视差值之和,当视差图中的某点dg(x,y)与先前求得的视差平均值davgX0的绝对差大于φ时,认为dg(x,y)是离群点,不统计该点的像素值,countQ表示相邻边缘点约束的非离群点以及非视差空洞点的个数,davgX表示剔除离群点后横轴方向上视差的平均值。运用上述方法,遍历整幅视差边缘图像。
同理,对于纵轴方向上的处理方法,参考横轴方向上的处理方法,遍历整幅图像。
完成上述操作后,优化后的视差中还留有边缘,应用式(22)、式(23)进行消除边缘:

其中,g(x,y)为边缘图像阈值分割后的二值图像,dg(x,y)为消去边缘后的视差边缘图像。将阈值分割后的边缘图像与得到的初始视差图进行与运算,得到被边缘所覆盖视差点的视差图,再将该图像与消去边缘的视差边缘图像相加,复原视差图d(x,y)。

由于同一边缘区域内的视差几乎是相同的,应用上述边缘约束视差的方法,有效地修正了视差图中的误匹配点以及视差空洞。
3.3 存在问题及解决方法
上述方法存在以下3 个问题:1)横向和纵向的单独处理会出现类似于动态规则算法的水平条纹;2)被边缘覆盖重现的视差点存在坏点;3)由于d(x,y)是由边缘约束处理而来,因此视差图中存在明显的边缘特征,一些同处于背景区域的物体,由于边缘约束的存在,使得不同物体之间的视差值存在微小差异。
针对上述问题,本文引入中值滤波消除条纹和部分坏点。而对于视差图中存在明显边缘特征的问题,本文提出基于视差图边缘约束的迭代聚类算法。
迭代聚类算法的核心在于边缘更新与迭代精度,假设d0(x,y)为初始视差图,取视差图d0(x,y)的边缘作为新的约束条件,重复3.2 节的步骤得到一次迭代下的视差图d1(x,y);取视差图d1(x,y) 的边缘更新约束条件,重复3.2 节。
假设第n次迭代后的视差图为dn(x,y),该视差图的误匹配率为Edn,若视差图的误匹配率满足:

则表明第n次的迭代结果满足要求,ξ为允许的最大精度。
迭代前后对比如图4 所示。从图4 可以看出,一些带有边缘特征的区域和视差坏点被消除。

图4 迭代前后视差对比Fig.4 Parallax comparison before and after iteration
4 实验结果与分析
实验使用的计算机操作系统为Win10 专业版,处理器为AMD Ryzen 5 2600X,主频为3.6 GHz,内存为16 GB,显卡为Nvidia GeForce GT 730(2 GB)。基于软件VS2013 和Opencv2.4.11 函数库进行仿真实验。实验所用标准图片均来源于国际公认的Middlebury[22-23]数据集。其中,Tsukuba 图像主要测试算法前向平行平面的匹配效果,Venus主要测试对不同斜面的匹配效果,Teddy 测试的是复杂场景下算法的鲁棒性,Cones 测试的是算法的整体性能。
将所得到的视差图与理想视差图进行比较,逐一判断像素点是否为正确的匹配点,得到视差图的误匹配率为:
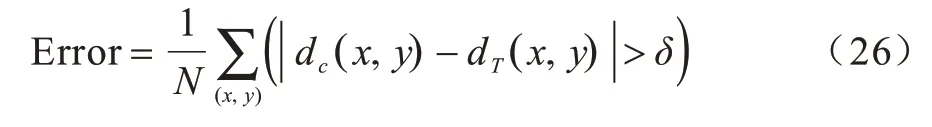
其中,N为总的像素点个数,dc(x,y) 为计算得到的视差图,dT(x,y)为真实视差图,δ为误差阈值。
4.1 实验1
为体现本文算法相对于其他匹配算法在匹配中的优势,本文选择在大小为7 的固定匹配窗口下,分别用SAD 算法、BM 算法、传统ASW 算法以及本文提出算法匹配代价改进的ASW 算法(Improved ASW),对Tsukuba、Venus、Teddy、Cones 4 幅标准图像进行匹配,并逐一比较,匹配结果如图5 所示。其中,从左到右依次为原图、SAD、BM、Traditional ASW 和Improved ASW。各算法误匹配率如表1 所示。

图5 不同算法的匹配结果Fig.5 Matching results of different algorithms

表1 各算法误匹配率Table 1 Mismatch rate of each algorithm %
从表1 的数据可以看出,Tsukuba 图像由于其场景的复杂性,匹配效果最差,各算法都没有取得很好的匹配效果,SAD 算法与BM 算法对右上角的低纹理区域都没有很好地进行处理,产生了大量的误匹配点。另外,BM 算法在台灯灯杆的视差不连续区域匹配效果很差。针对上述两种情况,传统ASW 算法克服了视差不连续区域的匹配问题,误匹配率相对于前两种算法而言,分别下降了7.07%和21.73%,但是对低纹理区域的误匹配并没有做到很好的抑制,而改进的ASW 算法则将两者都进行优化,相对于传统的ASW 算法误匹配率下降了1.26%。
Venus 图像的场景比较简单,低纹理区域也较少,各算法的误匹配率都相对较低,传统的ASW 算法对斜面的适应性不是很强,改进后的ASW 算法克服了这一问题,极大地提升了算法对斜面的适应性,使得误匹配率下降了近一半,仅有17.17%。
Teddy 与Cones 图像的视差范围都比较大,SAD算法不适合处理视差范围较大的匹配,因此,该算法的误匹配率较高。与传统的ASW 算法相比,改进的ASW 算法优化了视差图中存在的大量噪声点与少量的视差空洞,提升了性能,降低了误匹配率。
4.2 实验2
为体现本文算法对ASW 算法改进的有效性,选择了在大小为7 的匹配窗口下,代价改进的ASW 算法(Improved ASW)、代价改进+自适应窗口的ASW 算法(Improved ASW+Adaptive W)、代价改进+边缘约束与迭代聚类的ASW 算法(Improved ASW+edge)、代价改进+边缘约束与迭代聚类+自适应窗口的ASW 算法(Improved ASW+edge+Adaptive W)对Tsukuba、Venus、Teddy、Cones 4 幅标准图像进行匹配,并逐一比较。实验得到的匹配结果如图6 所示,从上到下依次为Improved ASW、Improved ASW+Adaptive W、Improved ASW+edge 和Improved ASW+edge+adaptive W。各改进算法误匹配率如表2 所示。

图6 改进算法的实验结果Fig.6 Experimental results of improved algorithm

表2 各改进算法的误匹配率Table 2 Mismatch rate of each improved algorithm %
从表2 的数据可以看出,自适应窗口算法无论是对于色彩多变,还是背景光照强度不一的复杂场景都有一定的提升作用,从Teddy 图像的匹配结果可以看出,与仅改进匹配代价算法的视差图相比,视差图中的空洞区域明显减小,这表明自适应窗口的ASW 算法优化了该低纹理区域的匹配。基于边缘约束的视差聚类算法以及基于视差图边缘约束的迭代聚类算法表现出了较好的性能,基于边缘约束的视差聚类算法消除了视差图中大部分的视差空洞以及异常点,提升了视差图的整体可靠性。迭代聚类算法从Tsukuba 图像与其他图像误匹配率的对比中可以看出(Tsukuba 图像经过5 次迭代,其他图像仅经过1 次迭代),经过多次迭代的视差图,其误匹配率的降低量明显要低于其他图像,表明了迭代聚类算法的适用性。
与文献[12-13]进行比较,文献[12]中Tsukuba图像的视差图在视差不连续区域出现了大量的误匹配点,图片中的物体失去了应有的边缘特征,边缘变形严重,得到的视差图效果极差。文献[13]中视差图的情况与其大致相同,并且在低纹理区域还存在一些视差空洞。在Teddy 图像的视差图中,文献[12]在小熊左下部分的低纹理区域出现小片的视差空洞。而文献[13]中的图像则表现相对良好,在Cones 图像中,文献[13]的视差图较为标准,文献[12]的视差图在圆锥尖峰处,笔筒上部出现少量误匹配的条纹区域。针对上述研究视差图中所存在的问题,本文的改进算法都对这些问题有了很好的解决方案,体现了算法较好的鲁棒性。
各算法及改进算法平均误匹配率如图7 所示。

图7 各算法及改进算法平均误匹配率Fig.7 Average mismatch rate of each algorithm and its improvement algorithm
综上所述,本文算法无论是在算法的鲁棒性还是整体性能上,都取得了一定程度上的提升。与SAD算法相比,误匹配率整体上下降了36.19%,相对于BM算法和传统的ASW 算法,整体上分别下降了18.03%和15.05%,表明了本文改进算法的正确性。
4.3 实验3
为体现本文中所提算法对低纹理区域匹配的有效性,以标准图像Teddy为例,选取一块具有代表性的低纹理区域,验证算法对低纹理区域的匹配具有提升作用,其匹配结果对比如图8所示。

图8 不同改进算法的低纹理区域匹配实验结果Fig.8 Experimental results of low-texture regions matching of different improved algorithms
从图8 可以看出,选取的标记区域是一块具有代表性的低纹理区域,在实验中选取不同算法对该区域进行匹配,匹配效果如表3 所示。

表3 低纹理区域匹配效果分析Table 3 Analysis of matching effect of low-texture regions
结合图8 和表3 可以看出,匹配代价的优化、自适应窗口算法以及基于边缘约束的迭代聚类算法都对低纹理区域的匹配效果有着提升作用。其中,基于边缘约束的迭代聚类算法效果最为明显,使低纹理区域的匹配效果得到显著提高。
4.4 实验4
在本文提出的自适应权重立体匹配算法中,分为以下3 个计算步骤:1)匹配代价计算;2)视差计算;3)边缘约束与视差聚类。假设N表示图像大小,代表全体像素,那么匹配代价计算的复杂度为O(N),视差计算WTA 算法的复杂度为O(1),因此,获得基本视差图的算法复杂度为O(N)=O(N)×O(1)。边缘约束与视差聚类属于视差图的后处理部分,独立运行于视差计算部分,其算法复杂度为O(N),因此,本文所提算法总的复杂度为O(N)。各标准图像的算法运行时间如表4所示。

表4 算法运行时间Table 4 Algorithms running timemin
本文算法基于传统的自适应权重立体匹配算法进行修改,虽然效率略低于传统算法,但是立体匹配的误匹配率明显降低,算法运行时间略微增加,主要是计算匹配代价时加入高斯差分以及后面的处理过程。
5 结束语
本文在传统自适应权重匹配算法的基础上,提出一种新的立体匹配优化算法。通过修改初始匹配代价,将高斯差分信息引入到代价匹配中,并加入边缘约束和视差边缘约束迭代聚类以及基于高斯差分图的自适应窗口算法,修补视差空洞与误匹配点。实验结果表明,该算法能够有效改善传统局部匹配算法不能较好地处理低纹理区域和视差不连续区域的匹配问题。下一步将使用GPU 对算法进行并行运算,加快程序的运行速度,满足实时性需求,并采用卷积神经网络,结合本文匹配代价的改进方法优化损失函数,利用训练好的网络模型,加快视差图的生成速度与复杂环境的处理能力。
