基于时空注意力机制的加油站级客流量预测
2021-04-29包恒彬马玉鹏杨奉毅韩云飞
包恒彬,马玉鹏,杨奉毅,韩云飞
(1.中国科学院新疆理化技术研究所新疆民族语音语言信息处理实验室,乌鲁木齐 830011;2.中国科学院大学,北京 100049)
0 概述
加油站流量可反映城市的能源消耗及经济水平,对加油站的客流量进行准确预测可帮助相关部门及企业制定更符合各站点实际需求的选址、运营以及调配策略,还可为需要加油的顾客提供推荐信息,以帮助其寻找排队时间最短的加油站[1]。
目前,针对加油站短时客流量预测的研究尚少,而加油站客流数据是一种典型的时空数据,这种时空特性使得加油站客流量预测问题与交通领域的其他问题具有概念上的相似性。早期研究通常采用如差分自回归移动平均(Autoregressive Integrated Moving Average,ARIMA)模型[2]及其改进方法来解决该类预测问题,而后期结合复杂特征工程与传统机器学习模型的方法被应用到该领域。然而,这些传统的时间序列模型或机器学习模型具有较大局限性,不能有效捕捉复杂的非线性时间与空间依赖的关系。
近年来,由于深度学习凭其优异的端到端学习能力而在解决自然语言处理、计算机视觉等领域任务时取得显著效果[3],因此研究人员逐渐将循环神经网络(Recurrent Neural Network,RNN)[4]和卷积神经网络(Convolution Neural Network,CNN)[5]应用到交通领域预测问题中。RNN 可对时间序列数据进行复杂建模并提取数据中的时间依赖关系,CNN 通过在像素级矩阵中不断进行卷积操作来捕捉数据间的空间相关性。同时,结合RNN 与CNN 构成一个复杂深度神经网络模型以克服传统方法的局限性,使得整个模型具有强大的时空数据多维非线性关联处理能力。将CNN 应用于大规模时空数据时需要进行特殊的预处理操作,目前主流的处理方法是将使用网格矩阵表示的时空数据转换为图像,以学习数据中的空间依赖关系。但该方法不适用于站点级的预测问题,且当网格设置较大时,同一网格会覆盖多个站点,无法满足所需的预测粒度。反之,如果网格尺寸小到只包含一个站点,则构成的巨大图像矩阵与冗余零元素将大幅增加计算量。
因为加油站客流数据在时间维度上具有以天为单位的周期性,所以结合最近几小时内的短期序列与过去几天的周期性序列,可以更准确地对数据时序依赖进行建模。然而,实际中加油站客流数据并不具有严格意义上的周期性,例如虽然每日的周期趋势大致相同,但是客流高峰出现的时段并不固定,且在一定范围内发生漂移,这种现象被称为周期性数据中的时间漂移。因此,仅对过去几天相同时段的周期性序列进行建模显然忽略了时间漂移所带来的影响。
受交通预测领域研究的启发,本文结合加油站客流数据特征,提出利用路网矩阵对站级客流数据进行建模,并使用基于注意力机制的时空网络(Attention Mechanism-based Spatial Temporal Network,AMSTN)模型同时捕获数据的空间与时间维度依赖关系,从而对加油站客流量进行预测。采用该模型对数据内空间与时间维度的关联关系分别进行建模,利用局部CNN捕获站点间的空间依赖关系,再采用多个长短期记忆(Long Short-Term Memory,LSTM)网络[6]建模短期与长期时间依赖性,并引入注意力机制修正时间漂移问题对长期预测结果的影响,以提高预测结果的准确性。
1 相关工作
加油站客流量预测问题与交通领域的相关预测问题具有相似性。本质上,交通预测的目标是预测某时间某位置的相关指标值,例如出租车需求量、区域客流量等,而这些指标的形成过程是相似的。因此,交通预测领域的相关研究工作可为加油站客流预测问题提供参考。交通预测领域中的现有模型大致可以分为基于传统机器学习方法的预测模型和基于深度学习的预测模型。
1.1 基于传统机器学习的预测模型
交通预测问题的主要研究对象是时空序列数据,它是一种特殊的时间序列数据,早期研究主要根据数据的时间维度进行预测,采用经典的时间序列预测方法依赖于特征工程和特征选择来获得较好的预测特征。传统的交通客流预测方法可以分为参数方法与非参数方法。其中,参数方法包括基于ARIMA 及其改进方法[7-9],非参数方法包括K-近邻(K-Nearest Neighbor,KNN)非参数回归法[10]、历史平均法(Historical Average,HA)与向量自回归法(Vector Autoregressive,VAR)[11]等。然而,基于ARIMA及其改进方法的模型依赖于不间断的输入序列,不适用于分析缺少数据的时间序列。HA 方法不能有效捕捉交通数据的动态变化(如周期性特征)。VAR方法可以捕捉相关时间序列之间的线性相关性,但忽略了预测值之间的相关性。由于上述方法仅考虑了时序特征,因此不能捕捉到数据间复杂的非线性时空依赖关系。
1.2 基于深度学习的预测模型
受图像识别领域的研究启发,现有的深度学习预测模型多数将同时段的预测量按空间位置建模为类似于图像的数据矩阵,并按时间顺序组织各时段的数据矩阵,为预测模型保留数据中丰富的空间与时间维度信息。文献[12]利用基于CNN 的网络模型捕捉空间依赖,并采用残差神经网络对城市人群流动进行预测。文献[13-14]使用基于RNN 的模型来建模时序依赖关系。虽然上述研究均明确对空间依赖或时序依赖进行建模,但它们都没有同时考虑空间与时间两种维度间的依赖关系。因此,文献[15-17]尝试结合CNN 与LSTM 的优势同时建模交通数据的空间和时间依赖性。文献[16]通过将卷积LSTM 单元与注意力机制相结合来增强代表性数据对每一步预测的影响权重。文献[17]采用局部CNN、LSTM 和语义图嵌入分别集成空间、时间和语义多个角度进行区域级出租车需求量预测。文献[18]提出门控机制和周期注意机制,使模型具有同时捕获静态与动态时空依赖的能力。
针对加油站领域预测的相关工作较少,文献[19]利用出租车GPS 数据,通过出租车在加油站的等待时间来估计加油站内的排队长度,并预测此时加油站内的客流量及销量。文献[20]将城市划分为网格空间,并结合多种深度学习网络建模区域内的时间、空间与语义三种维度的相关性,从而对区域级的油品销量进行预测。然而在加油站级客流量预测问题中,客流数据间的站级复杂非线性空间与时间依赖关系也是影响预测结果准确性的重要因素,而以上研究都没有进行相关的分析建模。因此,本文提出使用路网矩阵建模站级客流数据,并通过AMSTN 模型处理数据间复杂空间与时间维度依赖关系,实现对加油站级客流量的准确预测。
2 问题定义
将加油站站点集合定义为S={s1,s2,…,sM},时间间隔集合为T={t1,t2,…,tn},每个时间间隔t的长度为30 min。本文对客流记录、客流量及路网矩阵进行定义,并在此基础上对加油站级客流量预测问题进行形式化定义与描述。
定义1(客流记录)用三元组(o.t,o.s,o.uid)表示一条客流记录,其中,o.t、o.s和o.uid 分别为记录时间戳、加油站唯一编码与顾客唯一编码。
定义2(客流量)用表示站点s在时间间隔t内的客流量,=|{o:o.t∈T˄o.s∈S}|,|o|表示集合的基数。
定义3(路网矩阵)用Bt表示时间间隔t内所有站点客流量构成的路网矩阵。

路网矩阵大小为a×b,a、b分别为包含加油站的横向街道数与纵向街道数,将站点根据空间分布对应到路网矩阵的相近节点,节点值为一个站点在该时间间隔内的客流量(s∈S),无对应站点的节点值始终为0。
定义4(加油站级客流量预测问题)以路网矩阵的形式给定各加油站历史客流量{Bt|t∈T},并预测t+1 时刻各站点的客流量(s∈S)。
3 基于时空注意力机制的预测模型
本节将详细介绍本文提出的AMSTN 模型,该模型结合CNN、LSTM 与注意力机制同时捕获加油站客流数据中存在的空间与时间维度相关性。图1展示了AMSTN 模型的总体架构,时空数据首先输入到用于处理站点间空间依赖的CNN,CNN 提取出空间关联后,将输出分别输入到提供短期时序预测的短期LSTM 网络,以及引入了注意力机制修正时间漂移影响后提供长周期时序预测的长期LSTM 网络,结合2 个时序网络的输出得到网络的最终预测结果。

图1 AMSTN 模型架构Fig.1 Architecture of AMSTN model
3.1 局部CNN
CNN 通过持续的卷积操作可有效提取像素矩阵内的空间相关性,受此启发,本文使用CNN 提取站点间的空间依赖关系。采用路网矩阵对一个时间间隔内所有站点的客流记录进行建模,然后将该矩阵作为一维灰度图像输入到AMSTN 模型的CNN 组件中进行学习。但对整个矩阵直接应用CNN 会考虑大量的距离较远且相关性较弱的站点,削弱了CNN 对站点间强相关性的学习能力,从而影响整体预测性能。因此,本文使用局部CNN[18]仅对当前预测站点临近的局部范围采用CNN 网络提取站点间空间维度的依赖关系。
在一个时间间隔t内,以路网矩阵中一个节点i为中心,提取其周围D×D范围内所有节点的流量值,得到D×D大小的一维图像,并将其作为该节点的输入样本∈ℝD×D×1。图2 以路网矩阵中数值为6的节点为中心,取D=3 构造样本,位于矩阵边界的节点周围使用0 补全。
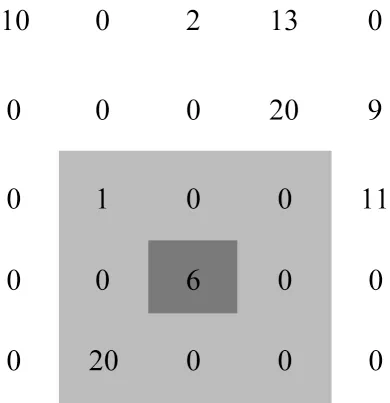
图2 D=3 时构造的样本Fig.2 Sample constructed when D=3
局部CNN 将提取出的原始输入作为输入到K层卷积层,使用二维卷积提取空间依赖,且每一层卷积公式为:

其中,k(k∈K)为卷积层数,*为卷积操作,使用ReLU作为激活函数,Wk和bk是需要学习的参数。在卷积操作后使用全连接网络将提取到的空间关联信息处理为LSTM 网络输入。
3.2 短期LSTM 网络
LSTM 网络对输入的隐状态向量,采用转移函数来解决RNN 网络在处理长序列时可能出现的梯度消失和梯度爆炸问题,从而达到在时序数据建模中具有更好的性能。本文使用一个LSTM 网络学习短期时序依赖,根据预测时间点前L个时间间隔的短期时序数据给出短期预测结果,网络输入的短期序列及LSTM 网络的简化转移公式可表示为:
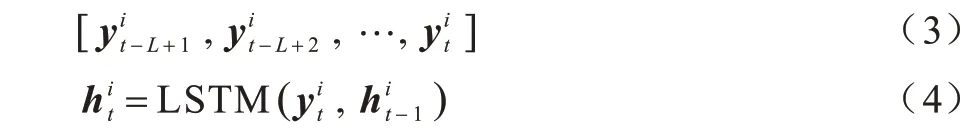
3.3 基于注意力机制的长期LSTM 网络
短期LSTM 网络仅处理预测时间点前几个时间间隔的短期时序依赖,忽略了以天为周期的长期时序依赖。然而仅增加序列输入长度会增大梯度消失的风险,削弱模型直接捕获长期时序依赖的能力。因此,本文使用与预测时间点相同时间的过去连续P日的数据构成长期序列(如P=2,代表昨天和前天的同一时间),将其作为长期LSTM 网络输入来捕获长期依赖进行预测,输入序列可表示为:

仅提取如式(5)所示的过去相同时间点序列进行长期时序依赖学习,忽略了周期性数据中的时间漂移问题。加油站客流数据虽然每日的趋势大致相同但并不具有严格意义上的周期性。图3 以某站点连续5 天的客流数据及客流高峰出现时间为例,展示了站点客流高峰出现时间会在一定时间范围内漂移的现象,这种时间漂移现象在加油站客流量时序数据中普遍存在。其中,图3 中的每个时间间隔为30 min。

图3 时间漂移现象示例Fig.3 Example of time drift phenomenon
本文通过引入注意力机制来修正时间漂移的影响,并得到最终的长期LSTM网络输入序列。如图1所示,采样过去P天中预测时间点前后共有Q个时间间隔的历史数据作为长期网络的输入样本。例如,如果预测的时间间隔是上午10:00—10:30,则需提取预测时间的前后1小时范围数据作为输入(即上午9:00—11:30,此时Q=5),使用LSTM提取每天的时序信息用于学习不同时刻对当天最终向量表示的贡献权重,应用的注意力机制及权重分配公式如下所示:

其中,为站点i在第p日预测时间点t的最终向量,为注意力贡献权重,s为贡献评分函数,vT、WH、WX与bX为学习的参数,表示站点i在第p日q时段的向量,为站点i在第p日q时段的CNN 网络输出。基于注意力机制的LSTM 网络组件的输入序列及预测网络可表示为:
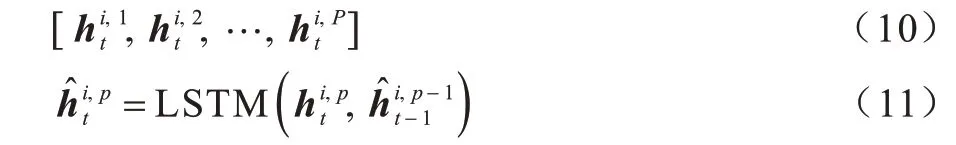
其中,为网络修正时间漂移现象影响后给出的长期预测。
3.4 融合训练

其中,Wf、bf为学习的参数,输出结果在[−1,1]内,将结果反归一化得到站点i在t+1 时刻的预测值。
4 实验与结果分析
4.1 数据集与预处理
本文以某市属行政区内所有加油站从2019-02-12—2019-04-02 共50 天的客流量数据作为数据集。数据集的前40 天用于训练与验证模型,后10 天用于评估模型性能。
将该行政区域构造成大小为11×11 的路网矩阵作为输入,并将站点按照在路网中的空间分布对应到路网矩阵的近似节点。使用30 min 作为数据处理的时间间隔得到各站点客流量数据,并对所有客流量数据进行最大-最小(Max-Min)归一化处理,处理后的数据分布在[0,1]。训练数据集的80%用于训练,20%用于验证。根据学术界及工业界经验,在测试模型性能时过滤客流量等于0 的样本不参与评估[18]。
4.2 实验参数设置
本文提出的 AMSTN 模型使用 Python、TensorFlow1.14.0 和Keras2.3.1 实现,并在真实加油站客流数据集上验证了该模型的预测能力。实验中AMSTN 模型具体超参数设置如表1 所示。

表1 AMSTN 模型的超参数设置Table 1 Hyper-parameter setting of AMSTN model
4.3 评价指标
实验使用均方误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)与平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)3 个标准评价指标对实验结果进行评价。3 个评价指标的计算方法如式(13)~式(15)所示:

4.4 结果分析
HA 模型使用各时段的历史客流平均值作为预测,LSTM 网络是一种改进的RNN 模型,其可以处理时间序列数据中的顺序依赖性,双向长短期记忆(Bi-LSTM)网络由前向LSTM 与后向LSTM 组合而成,其可同时从前后两个方向对时间序列进行建模。实验对HA、LSTM、Bi-LSTM 与本文模型的预测效果进行对比,结果如表2 所示,表中的数据是10 次实验结果的平均值。从表2 可以看出:在本文选择的数据集上,LSTM 与Bi-LSTM 模型的预测能力一般,虽然相比HA 模型在RMSE 与MAE 指标上有一定提升,但MAPE 结果表现略差,这是因为MAPE 指标对数据中的较低值更敏感,而仅考虑时序特征的方法更倾向于拟合数据中的较高值,所以出现RMSE 与MAE 指标提升而MAPE 下降的现象;3 个评价指标均验证了本文所提AMSTN 模型预测能力均优于其他3 种对比模型,与HA 模型相比,本文模型在RMSE 与MAE 指标上分别提高了22.89% 与21.39%。

表2 4 种模型的评价指标结果对比Table 2 Comparison of evaluation index results of four models
HA、LSTM 与本文模型对同一个站点连续两天的预测结果如图4 所示。其中,Ground Truth 为该站点两天内的实际客流量,且经过Max-Min 归一化处理,每个时间间隔为30 min。从图4 可以看出,本文模型相较于其他模型更贴近实际结果,且具有最佳的预测能力。

图4 本文模型与其他模型的预测结果对比Fig.4 Comparison of prediction results between the proposed model and other models
移除AMSTN 模型中部分组件的消融实验结果如表3 所示。其中:表3 中的AMSTN-S 模型是在本文模型的基础上移除注意力机制的长期LSTM 组件,仅使用局部CNN 组件与短期LSTM 组件提取数据中的空间依赖与短期时序依赖关系;AMSTN-L 模型是在本文模型的基础上移除短期LSTM 组件,仅使用局部CNN 组件与基于注意力机制的长期LSTM组件提取数据的空间依赖、长期时序依赖以及长期时序依赖中的时间漂移。

表3 消融实验结果对比Table 3 Comparison of ablation experiment results
从表3 可以看出:AMSTN-S 与AMSTN-L 模型的预测性能相比本文模型均有一定程度的下降,这是因为数据中的短期时序依赖、长期时序依赖和时间漂移因素共同提升了本文模型的预测准确性,而AMSTN-S 与AMSTN-L 模型在预测时分别遗失了部分时间维度依赖关系;AMSTN-S 模型的预测能力优于AMSTN-L 模型,这说明在预测时数据中的短期时序依赖相较于长期时序依赖和时间漂移对最终预测结果的影响更大。
为了考察空间CNN 输入样本大小与短期LSTM网络输入时序长度2 个重要超参数对AMSTN 模型的性能影响,本文进行不同超参数设置的对比实验,结果如图5 所示。从图5(a)可以看出:随着D值的增大,本文模型的预测性能呈下降趋势,当D=3 时输入样本大小为3×3,此时本文模型的预测性能最佳;当空间输入大小接近整个矩阵大小时,模型预测能力显著降低,这可能是因为过多弱关联数据削弱了本文模型中CNN 组件捕获与保存空间强关联关系的能力。从图5(b)可以看出:不同输入长度对预测性能的影响较大,当输入序列长度为6 时,AMSTN模型的预测性能最佳;随着输入序列长度的增大,模型预测能力逐渐稳定,但整个模型的训练时间明显增加。

图5 不同超参数对本文模型预测性能的影响Fig.5 Effect of different hyper-parameters on the prediction performance of the proposed model
5 结束语
针对加油站级客流量预测问题,本文提出一种基于时空注意力机制的深度神经网络预测模型。该模型通过路网矩阵对站级时空数据进行建模,并采用结合多个深度网络组件的模型处理站点间复杂的时空依赖关系。实验结果表明,该模型可对各站点的客流量进行准确预测。本文模型通过舍弃空间距离较远的数据输入来保障其预测性能,然而少量空间距离较远的站点间也可能存在强关联性。因此,下一步将从多源数据中提取少量的远距离强关联性站点关系,并将其与本文模型相融合,以进一步提升模型预测准确性。
