一种面向基站扇区方向角估计的改进SVM 算法

王 海，翁晨傲，李 克，骆 曦

（1.北京联合大学智慧城市学院，北京 100101；2.东南大学计算机科学与工程学院，南京 211189）

0 概述

电信运营商在运营和维护网络时，通常会使用基站信息表（Base Station Almanac，BSA）作为基础核心维护数据。BSA 指一个小区信息库，其中包含一个网络下的所有小区基本参数，例如小区所属基站类型、基站所在位置、小区天线参数（天线方向角、倾角等）和其他必要参数。其中，天线参数的准确设置对于保障基站覆盖质量具有重要作用。

BSA 中的数据主要来自运营商，且不对外开放，因此，很难被第三方获取。同时，BSA 是动态变化的，运营商优化和扩容网络的过程中会不断调整BSA 中的参数。目前，天线参数采集主要依靠人工上站测量，测量准确度、效率以及实时性等受人为因素影响较大。随着5G 的商用部署，网络规模进一步扩大，人工测量的方式局限性较大，迫切需要一种自动化方式进行参数采集与管理。

本文提出一种基于软间隔支持向量机（Support Vector Machine，SVM）的基站扇区方向角检测方法。以从海量用户终端上采集到的移动网络信息为基础，通过机器学习的方法准确估计基站天线的方向角，从而提高无线网络的运维效率。

1 相关工作

1.1 基站信息表及传统构建方法

BSA 一般包括站名、小区名、站址经纬度、小区标识、站型、方向角、俯仰角、站高和覆盖场景等信息，运营商需要持续获取基站信息以更新BSA，同时许多第三方机构也需要这些信息来分析用户的行为以及提供一些个性化的服务。因此，如何获取基站工参是一个重要的研究课题。

传统的BSA 数据是由运营商相关人员人工采集和上报，这种方式采集数据的步骤繁琐，会不可避免地产生测量误差，进而导致数据错误，此外，BSA 动态变化，逐级汇总数据导致数据的时效性减弱。

1.2 扇区方向角检测方法

BSA 的扇区方向角、下倾角和站址经纬度等工程参数是影响网络覆盖质量的关键。因此，运营商投入了大量的人力和物力来采集与优化这些关键工参。

目前，扇区方向角的检测主要采取人工现场逐站核查或在天线平台加装天馈测试仪表测量的方式，其过程耗时耗力、成本高昂且效率低下。因此，一些研究人员尝试利用其他数据源进行非现场方式的方向角估计。

文献［1］提出基于高斯分布的天线最佳方向角估计算法。首先，从数据采集平台提取终端上报的测量报告（Measurement Report，MR）数据，由于MR数据通常不包含样本经纬度信息，因此需要利用三角测量法定位样本位置；然后，求解各样本点与基站的距离以及相对于基站的角度；最后，根据高斯分布统计并确定扇区的最佳方向角估计结果。

文献［2］基于MR 数据，采用线性回归方法估计扇区方向角。基于传播模型估算采样点到基站的距离，根据样本分布将覆盖区域进行栅格化，取各栅格内场强最强的若干采样点计算其均值，筛选出大于均值的样本进行线性回归分析，将不同栅格内的样本拟合成一条直线，从而求解方向角。

高斯方法的假设前提是天线的部署会对准用户主要分布区域，在扇区中心方向上的用户样本密度最高，这一假设实际上会因为地理限制（如大型建筑、道路和水面等）而受到影响，因此，该方法实际上会对样本的空间分布非常敏感从而导致较大误差。此外，上述方法多基于MR 数据，而MR 数据中采样点缺乏精确定位信息，从而影响估计结果的准确性。

文献［3］对基于高斯分布的估计方法进行改进，提出一种基于径向栅格化的方向角估计方法。

1.3 基于MCS 的数据采集方法和数据介绍

随着智能终端的快速发展，基于众包的终端侧测量方法被广泛研究和应用［4-5］。文献［4］提出这类测量方法，并将其称为移动众包感知（Mobile Crowdsensing，MCS），文中将其又进一步分为参与式感知和机会感知两类。文献［6］将这类方法称为群智感知计算。MCS数据采集和分析方法［7］在网络运维、交通流量控制和大气环境质量分析等众多领域都得到了成功应用［8-10］。

针对网络侧MR 数据应用于方向角检测时存在的不足，本文利用MCS 数据研究基于机器学习的扇区方向角检测算法。将通过4G 网络MCS 覆盖数据采集平台所获得的数据作为研究对象，该平台通过终端系统提供的应用程序接口采集用户的网络覆盖采样数据，并在预先设定的条件下上传到采集平台，采集行为不会干扰用户使用。采样数据主要包括TAC、eNBID、cellID、经度、纬度、场强和信号质量等工参信息。

2 基于软间隔SVM 的扇区方向角检测算法

2.1 问题建模

在4G 和5G 移动网络中，标准的室外宏基站通常包括3 个扇区的定向基站，每个扇区分别采用一幅定向天线覆盖120°的范围。在网络建设及规划中，一般严格按照设计参数对天线的方向角进行设置和调整，如果在调整过程中有偏差，会造成弱覆盖、重叠覆盖或越区覆盖等问题，从而带来严重的信号干扰并影响用户的业务使用。

对于定向站小区，以其方向角为中心的扇形区域可定义为其覆盖区域。因为天线的方向图通常是轴对称的，方向角位于水平方向图的对称轴上，所以扇区方向角的估计问题可以转化为寻找相邻小区边界的问题。

为了保证用户在网络覆盖范围内移动时的业务连续性，相邻小区的覆盖边界需要有一定程度的重合以支持小区间的切换，此外，电磁波在空间中的传播随距离衰减但并不存在硬边界，相邻扇区的覆盖区域边界在实际情况下是一个线性不可分的模糊边界，无法通过传统的硬边界分类器来获取小区边界。因此，方向角估计的核心问题就是寻找最优的软分类边界。

作为统计学习的经典算法，VAPNIK 提出的SVM 在解决线性可分的二分类问题时具有优异的性能［11］。对于线性不可分问题，文献［12-13］在SVM的基础上，通过引入松弛变量和惩罚项提出一种软间隔SVM。后续有研究人员针对软间隔SVM 的核松弛变量、损失函数和可解释性等方面存在的不足进行改进［14-16］，并在岩矿石分类［17］、乳腺癌分型诊断［18］和建筑物抗震性能评估［19］等多个领域进行应用。

本文基于软间隔SVM 研究方向角估计问题。设同站下的任意2 个相邻小区S1和S2，分别有N1和N2个样本，这N1+N2=N个样本构成一个训练样本集D={(x1，y1)，(x2，y2)，…，(xN，yN)}，y∈{-1， +1}，其中，样本的属性字段仅保留经度和纬度，即为2D 属性空间。标记字段取为该样本所属小区，如果样本来自小区C1，则标记为+1，否则为-1。假设这2 个小区的边界为线性可分，则其边界即为能够正确划分上述训练样本集中正例样本和反例样本的线性超平面方程，如下：

因为无线信号在开放空间中传播的特性，相邻小区的样本会部分落在边界的对侧，即并非所有样本均满足如下的约束条件：

所以小区边界为软间隔边界。寻找最优软间隔划分超平面即为寻找满足式（3）的W、b和ξi最优值：

式（3）中采用了hinge 损失函数，ξi≥0 称为松弛变量，其反映样本违反约束条件的程度，ξi越大表示越宽容。C＞0 为一个预定义的常数，称为惩罚项。从式（3）可以推断出，当ξi一定时，C越大，对数据点的容忍度越高，越不愿意放弃该样本，相应的决策边界也越小。

此外，还需考虑的一个约束条件是对于共站的各扇区，根据基站的实际部署方式，其两两扇区边界均应满足通过基站站址x0的条件，则式（3）可重构为：

在式（4）中，ξi就是针对第i个样本点的分类损失，如果分类正确，则ξi是0。是总误差，其值越小则代表对训练集的分类越精准。原则上惩罚系数C可根据需要选择任意正数，C越大表示对于减小误差的要求越高，甚至不惜使间隔减小，当C趋于无穷大时，则不允许出现分类错误的样本，即硬边界SVM 问题通常会导致过拟合现象。

式（4）仍为一个凸二次规划问题，可以直接使用通用优化计算包求解，也可以将其转换为对偶问题后利用一些高效算法（如SMO）进行快速求解。为式（4）中的每条约束引入拉格朗日乘子：αi≥0，βi≥0，γ≥0，则式（4）的拉格朗日函数为：

式（4）的对偶问题可表示为：

对于多扇区基站而言，本文要解决的问题实际上是多分类问题。SVM 本身是一个二值分类器，在处理多分类问题时，需要构造合适的多类分类器。目前的多类分类器构造方法主要有直接法［20］和间接法2 类。其中，间接法通过组合多个二分类器来实现多分类器，主要包括OVR（One-Versus-Rest）和OVO（One-Versus-One）2 种。OVO 方法的缺陷在于当M越大时该方法需要越多的二分类器，两者呈二次函数关系，当M较大时，总训练时间和测试时间相对较长。

多扇区基站下的多边界分类问题是OVO 方法的简化形式，原因是其无需求解所有两两扇区的边界，而要寻找同一基站下径向相邻的两两扇区边界，即针对M扇区基站共需构造M个二分类器即可。OVO 方法的分类器数量与OVR 方法相当，并且不会出现严重的样本不平衡问题。

若同一基站中不同扇区下的采样数据严重不均衡，则需要设置平衡C参数，即对不同类别设置不同的惩罚系数C。设n个样本x1，x2，…，xn对应的标签分别为y1，y2，…，yn。假设存在标签为y={0，1}的2 类样本，其中，有m个标签为1的样本，其他n-m个样本标签为0。如果给定平衡参数，则通过y的值自动调整与输入数据中类频率成反比的权重，即：

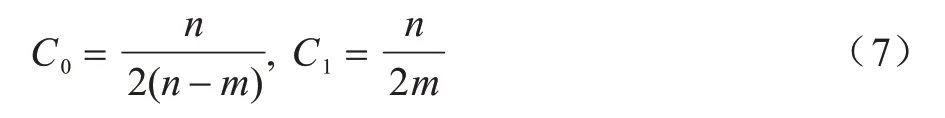
某一类的输入样本数越多，其惩罚项越小，这样就能有效缓解输入样本不均衡所带来的学习偏移问题。

2.2 基于软间隔SVM 的方向角检测

2.2.1 数据预处理

本文方法基于海量用户终端上实际采集的数据，具有数据量大、时空覆盖范围广、能真实反映基站实际覆盖等优势。但是，该方法也具有一致性差、定位精度偏低和受噪声影响等缺点，对方向角估计产生干扰。因此，需要对原始数据进行预处理。首先，直接删除关键参数缺失以及场强和信号质量等指标值溢出的采样点；其次，同一基站下的采样数据通过欧式距离过滤偏离值。具体地，对于采样点的重复值、缺失值，通过添加约束条件来进行筛选。对于由定位错误导致采样点位置偏移从而形成的孤立点，计算每个样本xi=（xi1，xi2）与基站站址x0=（x01，x02）之间的距离di，若di大于判决门限Td，则该样本为异常点，将其剔除。本文采用谷歌地图的近似计算方法，如下：

其中，R=6 378 137 m 为地球半径。

2.2.2 相邻扇区边界估算

从预处理后的网络覆盖采样数据集中，根据eNBID 字段提取同一基站的全部有效采样数据，将该基站内所有样本点的经、纬度作为属性集，各样本对应的小区ID 作为标记项。假设同一基站下有M个小区（顺时针排列，依次记为C0～CM−1），利用2.1 节方法，通过OVO 线性内核的SVM 训练后得到的线性边界依次为Margin（Ci，Cmod（i+1，M）），i=0～（M−1），即：

图1 所示为三扇区基站下经过SVM 训练后得到的超平面（实线）及其对应的最大间隔平行线（虚线），彩色效果见《计算机工程》官网HTML 版，下同。只需保留3 条过站址的射线，以站址为原点，采样点数量较多的区域方向为射线方向，本文将该过程称为确定边界的矢量方向。

图1 三扇区基站的SVM 超平面及最大间隔平行线Fig.1 SVM hyperplane and maximum interval parallel line of three sector base station

2.2.3 扇区方向角计算

在确定相邻扇区边界后，可根据过站址的边界垂线两侧的样本量分布来确定边界矢量方向。设有任意2 个相邻小区S1和S2，总样本量为N，则边界垂线两侧的样本数Sup和Sdown分别为：

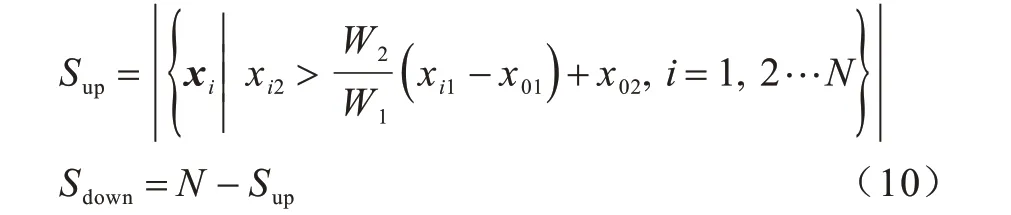
其中，Sup和Sdown取值较大的一侧为边界矢量V的方向。

取每个小区与其两侧相邻小区间的边界矢量间的夹角平分线作为该小区的张角，取该张角的等分矢量方向和正北方向的夹角为该小区的方向角。以LTE 网络下的方向角估计为例，基于软间隔SVM 的扇区方向角估计算法描述如下：

算法1基于软间隔SVM 的扇区方向角估计算法

3 算法性能评估

本文利用在上海LTE 网络中通过MCS 方法采集的海量终端实测数据集，将所提方向角估计算法与高斯方法、径向栅格化方法进行实验对比。

3.1 单站对比分析

为了更好地呈现软间隔SVM 算法的效果，本文分别选取城区基站A 和郊区基站B 进行方向角估算分析，基站的具体信息如表1 所示，2 个基站均为标准的三扇区基站，样本量分别为35 007 和74 576。

表1 2 个基站在BSA 中的基本信息Table 1 Basic information of two base stations in BSA

以基站A 为例，训练后所得各扇区之间的超平面及对应的最大间隔平行线如图2所示，进一步通过式（10）确定扇区边界的矢量方向如图3 所示。从中可以看出，经过训练得到的边界可以较好地区分各扇区。

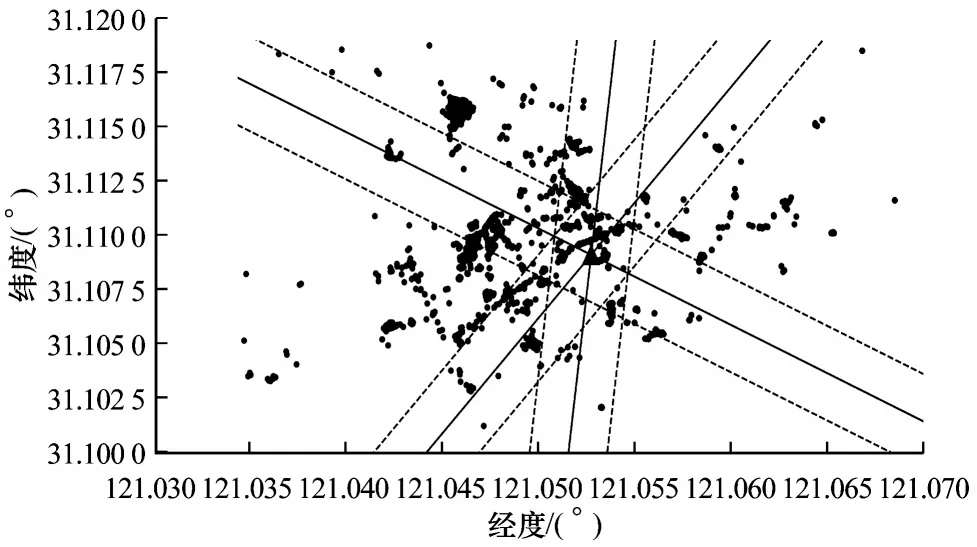
图2 基站A 各扇区之间的超平面及对应的最大间隔平行线Fig.2 The hyperplane between the sectors of base station A and the corresponding parallel lines with maximum spacing

图3 基站A 各扇区之间的矢量边界Fig.3 Vector boundary between sectors of base station A

分别使用高斯方法、径向栅格化方法和SVM 方法对以上基站的扇区方向角进行估计，城区和郊区的方向角估计结果分别如图4 和图5 所示，图中紫色、绿色和红色样本点分别来自3 个扇区，颜色深浅代表不同的场强值，黑色三角形为基站站址位置，虚线代表各扇区之间的实际边界，绿色箭头为真实扇区方向角，蓝色、红色和黄色箭头分别代表径向栅格化方法、软间隔SVM方法和高斯方法对方向角的估计结果。

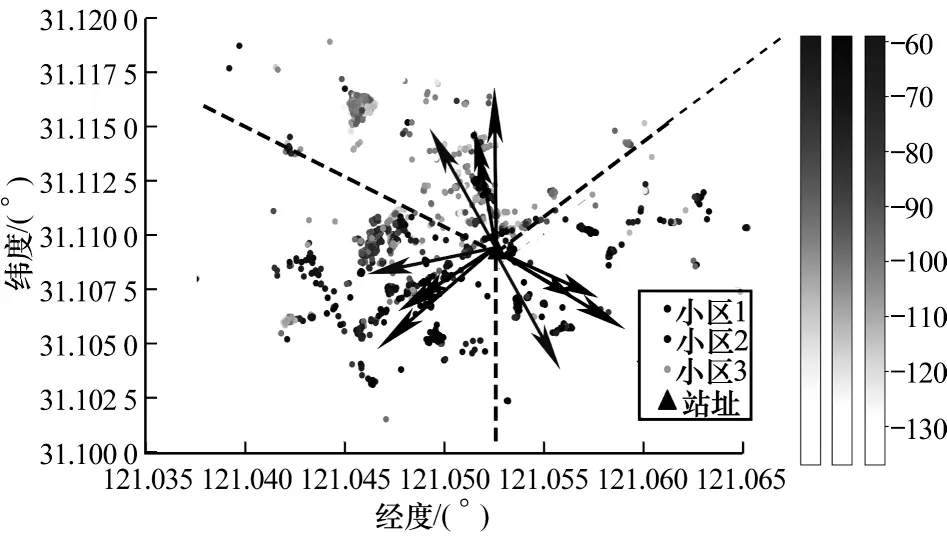
图4 基站A 的方向角估计结果Fig.4 Azimuth estimation result of base station A

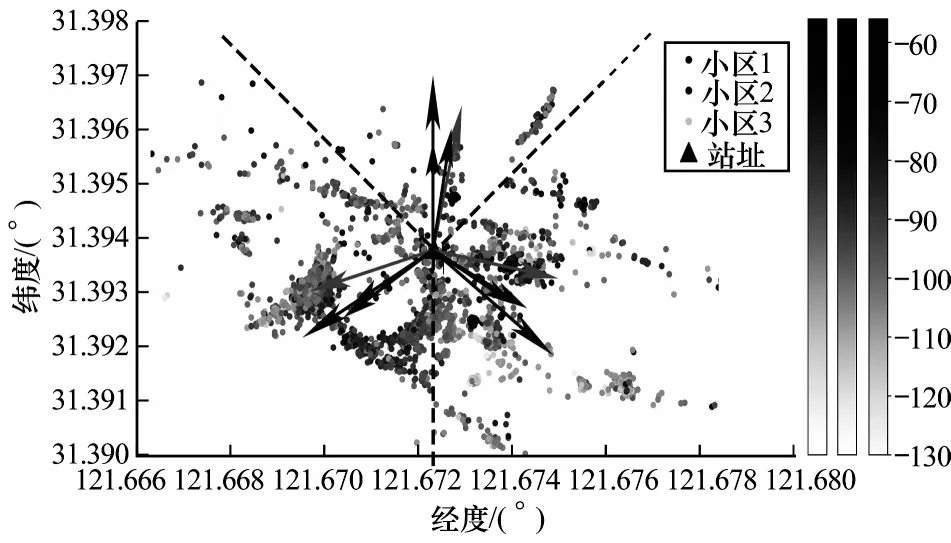
图5 基站B 的方向角估计结果Fig.5 Azimuth estimation result of base station B

从图4 和图5 可以看出，径向栅格化方法和软间隔SVM 方法均表现出优越的性能，方向角估计结果几乎与实际方向角重合，而高斯方法主要指向最大样本数的角度，造成了明显的误差。表2 所示为各方法估计的方向角值。从表2 可以看出，对于基站A，各方法对方向角估计的平均误差从左到右依次为2.3°、6.0°和23.3°，对于基站B，各算法对方向角估计的平均误差从左到右依次为5°、2.3°和15.3°，通过对比可知，径向栅格化方法和软间隔SVM 方法的性能均优于高斯方法。

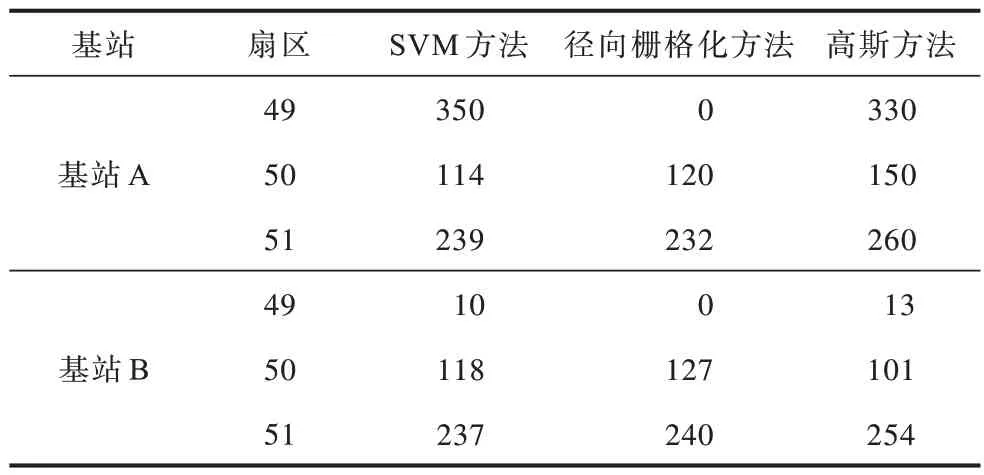
表2 3 种方法的方向角估计值Table 2 Azimuth estimation of three methods（°）

3.2 样本特征对算法性能的影响

3.2.1 共站扇区样本量分布不平衡的影响

由于周围环境和数据采集时间不同，因此在实际样本空间中，往往不同扇区下的样本量存在较大差异，这会带来较大误差。因此，需要控制不同扇区样本的权重，以达到最佳的分类效果。通过式（7）可对样本不平衡的模型进行训练，并得到较好结果。以基站B 为例，图6、图7 分别为采用平衡C参数和不采用平衡C参数的估计结果，可以看出，紫色样本小区与相邻小区的边界受样本量影响较大，当采用平衡C参数时，小区分类超平面向样本量较多的一侧偏移，从而有效降低了样本量对分类边界的影响。

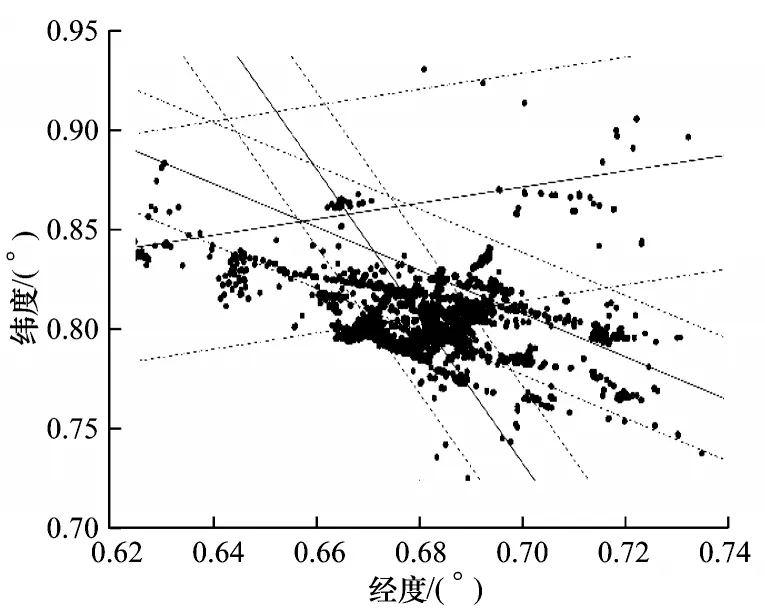
图6 未加入平衡C 参数的软间隔分类边界Fig.6 Soft-margin classification boundary without balanced C parameter

图7 加入平衡C 参数的软间隔分类边界Fig.7 Soft-margin classification boundary with balanced C parameter

3.2.2 样本量的影响

以基站B 为例，统计不同样本量下各方法估算结果的平均误差，结果如表3 所示，通过对比可以看出，随着样本量的降低，径向栅格化方法性能显著下降，高斯方法也有一定程度的下降，而SVM 方法能够保持相对稳定的准确率，表明其具有较强的鲁棒性。

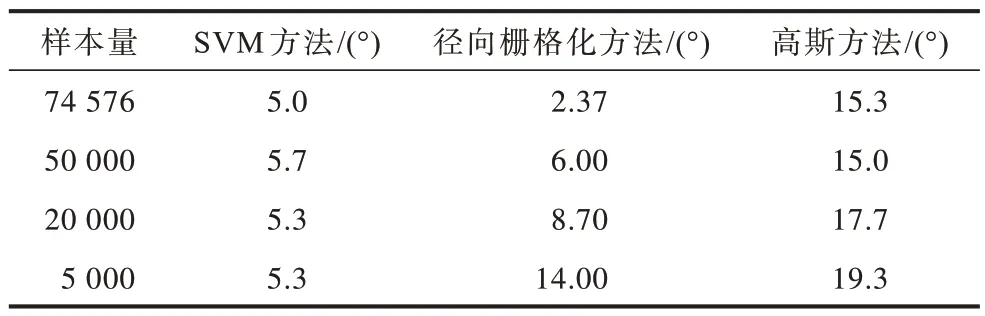
表3 不同样本量下3 种方法的方向角估计平均误差Table 3 Average error of azimuth estimation of three methods under different sample sizes

3.3 多站统计分析

本文进一步对多个基站下的各方法性能进行统计和对比。为了保证估计效果，统计各基站的样本量，并剔除样本量不足4 000 的基站，对符合条件的130 个基站利用3 种估计方法进行实验对比，各基站的具体估计误差CDF 分布如图8 所示。从图8 可以看出，SVM 方法、高斯方法和径向栅格化方法的平均估计误差分别为20.85°、29.03°和24.38°，SVM 方法的评估性能明显优于2 种对比方法。

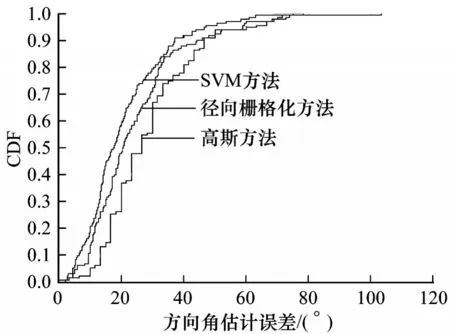
图8 多基站下3 种方法的方向角估计误差CDF 分布Fig.8 CDF distribution of azimuth estimation error of three methods under multi base stations

4 结束语

基站扇区方向角作为基站信息表的关键参数，对运营商的日常网络运维与优化具有重要意义。本文提出一种基于软间隔SVM 的基站方向角估计方法，以提高方向角估计的准确性，降低对数据量的依赖，避免传统运维中由人工采集与管理数据所带来的时延和误差，并有效解决第三方无法获得重要基站工参的问题。实验结果表明，该方法通过少量样本就能得到精度较高的方向角估计结果。下一步将利用采样数据中除经纬度之外的其他属性信息，尤其是场强和信号质量信息，在更高维的属性空间中实现最优边界估计，从而对估计方法进行优化，提高方向角的估计精度。