Markovian忆阻二阶BAM神经网络的非脆弱指数状态估计

罗 玲 蹇继贵 郑 胜

(三峡大学 理学院,湖北 宜昌 443002)

双向联想记忆(BAM)神经网络由B.Kosko在1987年首次提出,该网络近年来在联想记忆、机器人控制、信号处理等方面有着重要应用.众所周知,惯性项会导致神经网络的分岔和混沌.在传统神经网络中加入惯性项得到的二阶神经网络引起了学者们的研究兴趣,并取得了许多有趣的结果[1-4].

忆阻器与生物突触在外界刺激下的电导变化惊人地相似,它是记录和更新突触权重的理想材料,因此忆阻器可以模拟神经网络中的电突触.近年来,将神经元的激活结构与记忆连接权重相结合的忆阻神经网络掀起了一股研究热潮.由于外界突然的干扰和环境的变化,实际系统的结构不断变化,信息锁定现象经常发生.具有信息锁定的网络可能具有有限的模式,并且模式可以在不同的时间从一种模式跳转到另一种模式.Markov链驱动的动态系统已被证明适合于模拟由大量突发随机变化引起的系统.因此,具有这种跳跃特性的忆阻神经网络可以由一种与Markov链相一致的忆阻神经网络转化而来,称为Markovian忆阻神经网络.目前,已存在较多关于Markovian忆阻神经网络动态性能的研究[5-7].然而,当前对于Markovian忆阻二阶BAM神经网络的研究较少.

在实际应用中,由于网络拥塞、丢包、丢失测量数据等原因,我们往往难以获取所有神经元的状态信息.然而,状态信息往往需要被了解才能达到一定的实际性能.因此,利用已有的网络输出测量值来估计神经元的状态具有重要意义.事实上,由于设备老化、模数转换或舍入误差等原因,当状态估计器以数字方式实现时,实现误差往往是不可避免的.因此,为了保证系统的稳定性,设计的估计器应允许一定的非脆弱性,使估计器参数在一定范围内变化时,系统能够满足给定的性能指标.当前,已经有了一些关于神经网络非脆弱状态估计的研究结果[8-11],但几乎没有关于Markovian忆阻二阶BAM神经网络的非脆弱指数状态估计的研究报告.基于上述考虑,本文研究时变时滞Markovian忆阻二阶BAM神经网络的非脆弱指数状态估计问题,并通过求解LMI,得出估计器的显式表达式.

1 预备知识

1.1 模型描述

本文中,Rn表示n维欧氏空间,Rn×m表示n×m维实矩阵的集合,上标T表示转置,*表示块在矩阵中的转置,λmax(W)和λmin(W)分别表示矩阵W的最大特征值和最小特征值.W＞0表示W是对称正定矩阵,I表示单位阵,C([-∞,0],Rn)表示连续函数集.Z={1,2,…,n},Z~={1,2,…,m}.

令{a(t),t≥0}是定义在(Ω,F,P)上取值于有限状态空间S={1,2,…,N}右连续的 Markov过程[6],其转移概率为:

本文探讨如下Markovain忆阻二阶BAM神经网络:

其中神经元状态向量

系数矩阵Aℓ,Cℓ,Bℓ,Dℓ为正定对角阵,时滞ϑ(t)和θ(t)对于常数τ1,τ2,e1,e2满足

激活函数

外部输入u(t)∈Rn,v(t)∈Rm,

其中

切换跳跃值λq＞0,权重是常数.令

介绍如下符号:

其中i=1,2;j=3,4;Z=E,R;J=F,K;ζp∈Rn,ξp∈Rm,ζp与ξp的第p个元素为1,其余元素为0,(t)Γi(t)≤I,i=1,2,3,4.

类似文献[10]中的分析,系统(1)可改写为:

假设1:对于任意的x,y∈R(x≠y),有常数存在,使得下式成立:

系统(2)的测量输出为:

其中:χκ(t)∈Rn,χμ(t)∈Rm为测量输出,是已知的常矩阵,非线性扰动σ1:R×Rm→Rm,σ2:R×Rn→Rn满足下列不等式:

注1:与文献[10]中存在两个自由权重矩阵的测量输出不同,本文在测量输出(4)中引入了4个自由权重矩阵文献[9-11]中的测量输出为本文测量输出的特殊形式,因此本文的测量输出更具一般性.

系统(2)的估计器为:

系统(5)的测量输出为:

其中κ(t)的估计值的估计值Rm.估计增益

随机变量ε1(t),ε2(t)∈R是在(0,1)区间取值的伯努利分布序列,描述控制器增益波动随机发生的可能性,Pr{ε1(t)=1}=ε1,Pr{ε1(t)=0}=1-ε1,Pr{ε2(t)=1}=ε2,Pr{ε2(t)=0}=1-ε2,ε1,ε2∈[0,1]为已知常数.为实对角矩阵为增益波动,形式如下:

注2:当ε1=0,ε2=0,系统(6)为(2)的普通状态估计器.

注3:本文考虑了与增益矩阵相关的增益波动,其发生概率服从伯努利分布.文献[11]将增益波动发生的概率取为1.因此,本文的研究结果更具有现实意义和通用性.

可得到误差系统为:

系统(9)的初始值为:

定义如下符号:

1.2 基本定义和引理

定义1[3]若存在正数ω＞1,e＞1使得下式成立:

则称系统(6)为系统(2)的指数状态估计器.

引理1[12]对实矩阵Ξ(t),N,M,有ΞT(t)Ξ(t)＜I成立,则对任意的υ＞0,下式成立:

2 主要结果

定理基于假设1和假设2,若存在数β1＞0,β2＞0,矩阵对角矩阵Xi＞0,(i=1,2,3,4),矩阵使得下式成立:

Ω中其余元素全为0.那么系统(6)是系统(2)的指数状态估计器,其增益矩阵是

证明:构造如下Lyapunov泛函:

计算V(t)沿着(7)的随机导数,有:

根据假设2,可得:

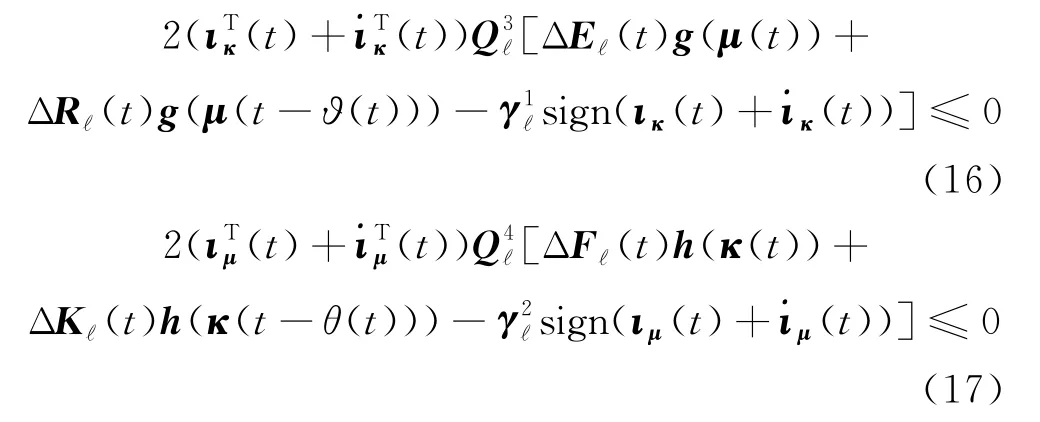
由假设1,对于对角矩阵Xi＞0,(i=1,2,3,4),有:

由式(4)可得到:

将式(16)和式(17)代入式(14),并将其与式(13),(15),(18)～(23)整合可得:

对式(8)进行Schur补运算,结合引理1,有:

因此,LV(t)＜0,V(t)＜V(0).

所以可得到:

由定义1可知系统(6)是(2)的指数状态估计器.

注4:已存在关于一阶神经网络[8,11]和分数阶神经网络[9,10]的非脆弱状态估计问题的研究,但是还没有关于时变时滞Markovian忆阻二阶BAM神经网络的非脆弱指数状态估计问题的相关研究.因此,本文的研究结果是新的.

注5:文献[4]通过变量替换将惯性神经网络转换成普通一阶神经网络研究了其状态估计问题,本文直接研究了BAM二阶神经网络的非脆弱指数状态估计问题,且本文系统中考虑了Markovian跳跃参数,因此本文的研究丰富了已有研究结果.

3 数值仿真

考虑系统(1)具有两个模态,参数如下:

由假设1可知:

由式(5)得:^Z1=0.4,^Z2=0.6,取

由假设2经过简单计算可得:

求解LMI(8)可得:

因此,由定理可知,系统(6)是(2)的指数状态估计器.

图1描述状态κ1(t),μ1(t)与其估计值的轨迹,图2描述状态κ2(t),μ2(t)与其估计值的轨迹,图3描述估计误差渐近收敛到0,图4描述Markov链.

图1 神经元状态κ1(t),μ1(t)与其估计值轨迹

图2 神经元状态κ2(t),μ2(t)与其估计值轨迹

图3 估计误差

图4 Markov链

4 结 论

基于Lyapunov泛函方法,不等式技巧以及Barbalat引理,本文研究了Markovian忆阻二阶BAM神经网络的非脆弱指数状态估计问题,给出了证明估计器存在的充分条件.通过引入测量函数,将目标系统转换为不确定系统,避免了大量的计算负担.最后给出了仿真结果证明了所设计的估计器的可行性.笔者后续将研究二阶BAM四值神经网络的非脆弱同步问题.