采用增广乘子法和免疫算法的混合可靠性分析
2021-04-29彭云龙王林军杜义贤
彭云龙 王林军 杜义贤 黄 杨 廖 玮
(1.三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002;2.三峡大学 机械与动力学院,湖北 宜昌 443002)
随着现代机器结构的复杂化和精细化要求的日益增加,亟需一种将多方面因素综合考虑的计算模型来进行可靠性优化评估.为此,研究者们为了解决实际工程问题,提出了许多新的计算方法[1-8].潘柏松等[9]针对随机变量和非独立区间变量共存的情况,提出一种基于椭球模型,利用高维模型表示方法(HDMR)解耦变量的快速可靠性计算模型,并利用多项式近似,得到一种混合单步可靠性计算方法,仅需要较少的函数调用次数,就可得到较高精度的计算结果.陆海涛等[10]以重要抽样的方向为进给方向,以坐标轴与主线性逼近失效面的交点和设计点的方向作为搜索次线性化点的方向,构建线性凸区,提出一种通过概率方法的线性凸区法,克服了强非线性极限状态方程的可靠性评估问题,具有较高的计算精度.张航等[11]在拉丁质心Voronoi网格化抽样方法生成的样本的基础上,建立功能函数的支持向量机回归代理模型,该方法在可靠性分析中具有精度高、鲁棒性好等特点.王林军等[12]在改进一次二阶矩法的基础上引入了参数的不确定性,探索了不确定性对可靠性指标的影响.王国富等[13]利用改进的子集模拟法对U型梁结构进行了可靠性分析,缩小了相对误差,使得计算结果更加精确.刘强等[14]从失效物理分析的角度出发建立性能退化模型,并利用贝叶斯方法将寿命模型和性能退化模型进行整合,得到可靠性评估模型.
对于现有的可靠性评估方法,蒙特卡罗模拟法(MCS)能放松对理论模型的理想化需求,并且可以作并行计算,适用于大型复杂结构系统,但计算步数过大,耗时较长,一般作为相对精确解或用来验证的近似解析解.一次二阶矩法(FOSM)计算简便,避免了大量的数值计算,同时具有收敛快、迭代次数少、精度高等特点,适用于变量独立、正态分布、对数正态分布的线性极限状态方程,但对于非线性程度较高的极限状态方程效果较差,甚至无法求解,且对变量的分布标准有一定要求,在实际工程中具有一定的局限性.免疫算法是一种全局搜索智能优化算法,具有收敛速度快、自适应性强、鲁棒性高等特点,克服了强非线性极限状态方程的求解问题,且对于变量分布标准没有特殊要求.增广乘子法将拉格朗日乘子法和罚函数法进行结合,使其兼具乘子项和惩罚项的优点,收敛速度快,并能将有约束问题转化成无约束问题.
本文提出一种采用增广乘子法和免疫算法的混合可靠性分析方法,有效避免了初始罚因子对求解结果的影响,并将参数相关性考虑进来,运用免疫算法对模型进行求解.
1 可靠性优化设计数学模型的建立
1.1 可靠性指标的建立
结构的可靠性往往受到结构的材料、所受的应力以及结构的几何形态和尺寸的影响,且这些参数又具有不确定性,因此在可靠性分析中,通常将这些称为基本随机变量.假设有n个随机变量,用Xi(i=1,2,…,n)表示,用g(X)表示结构的功能函数[15]:

式中:Z的取值决定了结构所处的状态;当Z>0时,结构处于可靠状态;Z<0时,结构或机器处于失效的状态;Z=0时,结构处于极限状态.Z=g(X)=0称为极限状态方程,在坐标系上生成的曲面为极限状态面,又称失效面.
当结构的功能只与载荷效应S和结构抗力R有关时,功能函数可写为Z=(R,S)=R-S,此时结构所处的状态与上述相同.
结构可靠度表示机构在寿命周期和使用环境下能够完成预定作业功能的概率,常用Ps(变量x的联合密度函数fx在可靠域Ωs的多重积分)表示:

失效概率表示机构在寿命周期和使用环境下不能完成预定作业功能的概率,常用Pf(变量x的联合密度函数fx在可靠域Ωf的多重积分)表示:
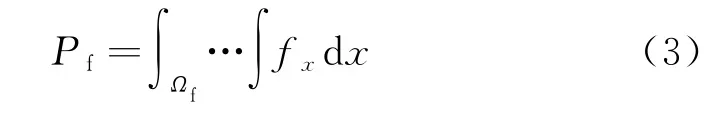
可靠度与失效概率必然是相辅相成的,其关系为:

可靠性指标:采用R-F(拉科维茨-菲斯莱法)将一些非正态的变量转变为标准的当量正态化,获得均值,标准差,可靠性指标β等正态分布的变量:
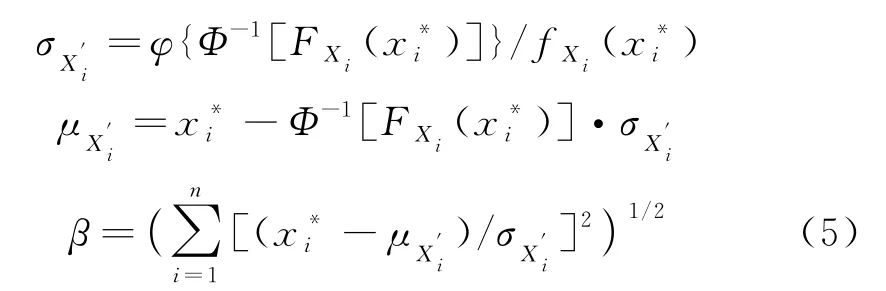
其中:φ(·)为标准正态分布下的概率密度函数;Φ-1(·)为标准正态分布下的累积概率分布函数的反函数;FXi(·)为Xi累积概率分布函数;fXi(·)为Xi累积概率密度函数为优化后的设计点.可将β看作是坐标原点到极限状态面的最短距离,极限状态面上对应的点就是设计点或验算点,数学模型见式(6):
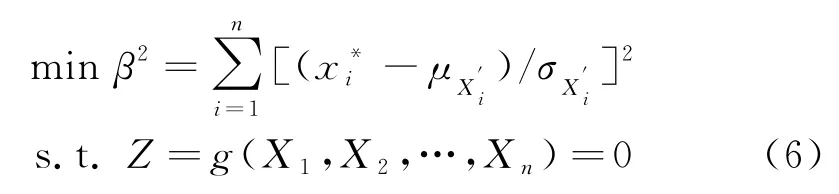
1.2 增广乘子法
罚函数法是一种通过序列不断逼近的求解方法,可以适用于大部分优化问题.同时罚函数法可以和大多数的无约束优化算法进行结合,但该方法收敛速度过慢且求解结果受初始罚因子影响较大;因此,本文采用增广乘子法引入乘子项和惩罚项,使得收敛速度更快,对罚因子的取值也没有过多的要求,只需要取较大的罚因子即可,或者按照一定的比例进行递增.首先建立一个等式约束的模型[16]:

其中:f(x)为目标函数;hv(x)为约束函数.
通过拉格朗日乘子将式(7)的等式约束转化为一个无约束优化问题:
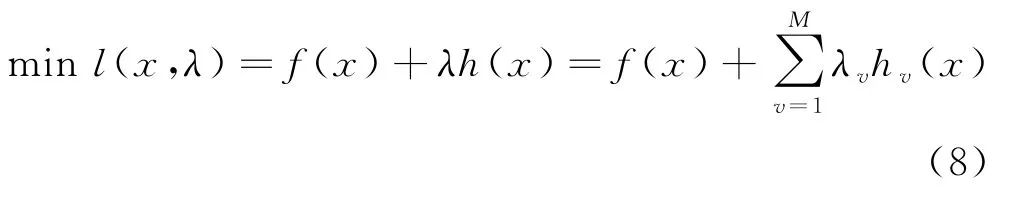
式中:λ为拉格朗日乘子.应用拉格朗日乘子法构造成一个无约束函数,如式(9)所示:

式中:右边第一项f(x)为目标函数;第二项为惩罚项,r为罚函数法的罚因子;第三项为乘子项.
2 免疫算法
免疫算法是根据生物的免疫系统和基因进化的工作原理模拟出来的一种具有高鲁棒性、自适应性、全局收敛性、可并行搜索的智能优化算法.它运用自身产生多样性种群,并在每一次种群刷新前对抗体浓度进行评价,抑制浓度过高的个体,从而保证了个体的多样性.免疫算法通过亲和度计算来评价抗体浓度的大小,然后给予亲和度大和浓度低的抗体一个较大的激励度,通过克隆算子和变异算子将上一代中的优异个体遗传给下一代,同时删除激励度较低的个体,以达到种群更新实现全局最优搜索的目的.其算法与免疫系统一一对应,见表1.
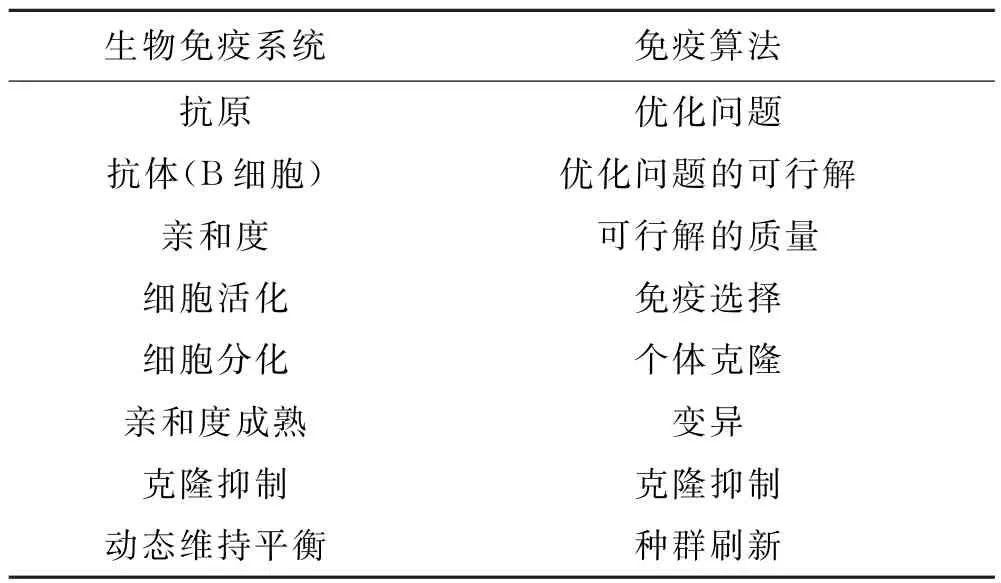
表1 免疫算法与免疫系统对应关系
免疫算法中最为重要的几个算子的评价公式[17]如下所示:
1)亲和度算子

2)浓度评价算子

3)激励计算算子

其中:abi表示种群中的第i个抗体,abi,k表示第i个抗体的第k维.
迭代过程如图1所示.
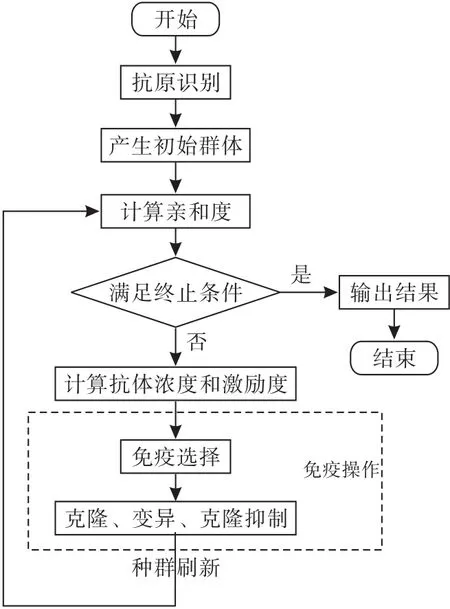
图1 免疫算法流程图
3 数值算例
考虑一组由变量x1,x2构成的极限状态方程

其中:x1与x2均服从正态分布,其均值μ分别为10和2.5,标准差σ分别为2和0.375.
使用本文算法,取罚因子r为1 000,拟定染色体数目NP=50,最大遗传代数即运算终止条件为12代,变异概率Pm=0.7,激励度系数α=1,相似度阈值δ=0.2,克隆个数Ncl=10,结果如下所示:
1)本文方法目标迭代12次,第4次收敛,MPP点为(10.666 2,1.629 1),可靠性指标β=2.346 3,失效率Pf=0.009 5.
2)采用FOSM法通过梯度对目标函数进行最优搜索,目标函数在第12次收敛,MPP点为(11.1855,1.654 9),β=2.330 2,Pf=0.009 9.
3)采用MCS法,对目标函数进行1×107次抽样模拟,β=2.345 9,Pf=0.009 5.
本文方法计算结果见表2~3.根据表2、表3以及图2可知:本文方法相对于FOSM法收敛更快;可靠性指标及失效概率接近MCS法的值,具有较高的精度;本文方法切实可靠,并且能有效避免工程案例中罚因子的选择和求导困难等问题.

表2 本文方法迭代信息表
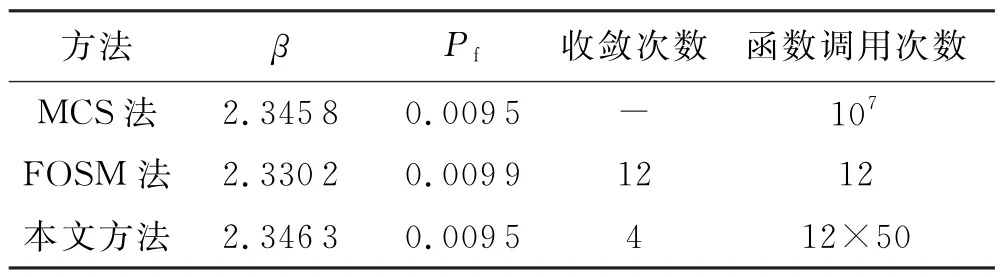
表3 3类方法结果对照表

图2 本文方法与FOSM法计算结果对比图
4 车辆侧面碰撞算例
对车辆侧面碰撞进行可靠性优化设计,有限元模型[18]如图3所示,极限状态方程可以表示为


图3 车辆侧面碰撞有限元模型
其中

式中:g(x)为汽车响应面方程;R(x2,x3)代表车辆侧防撞量;R(x5,x6)代表护栏防撞量,各变量对应关系见表4.

表4 随机变量关系
采用MCS法对其进行1×107次抽样模拟,β=4.164 5,Pf=1.560 0×10-5.采用本文方法计算,其MPP点为(0.997 7,0.996 1,0.9961,0.997 8,0.312 4,29.998 6,-10.710 5),β=4.003 0,Pf=3.127 7×10-5.两种方法计算结果对照表见表5,亲和度进化曲线如图4所示.

表5 MCS法与本文方法计算结果对照表

图4 亲和度进化曲线
根据表5可知:本文方法与MCS法的计算结果较为接近,本文方法切实可靠,具有一定的精确度;根据图4可知:本文方法在第150次迭代时已收敛,其后数值趋近平稳,对非线性问题具有良好的收敛性和平稳性.
由于车辆侧碰的可靠性评估极为复杂,其失效形式并不是由某个单一变量的变化而决定的,而是一个整体联动的过程.因此,考虑到变量之间的相互关系,在做可靠性分析时引入相关系数,做相关度分析,其可靠性指标见公式(16).考虑到车门防撞量(x2)和车门腰线加强板(x3)、护栏高度(x6)和护栏高度位置(x7)之间的相关性,拟定相关系数[19]ρx2x3=0.4~0.8、ρx6x7=-0.4~-0.8.

现考虑5种工况,当ρx6x7在-0.4~-0.8变化时,ρx2x3分别为0.4,0.5,0.6,0.7,0.8这5种情况下,可靠性指标的变化趋势.
采用本文方法进行求解,并将求解结果以三维坐标形式呈现,如图5所示.

图5 相关系数与可靠性指标对应图
根据图5可知:随着|ρx6x7|的逐渐增大,β不断下降,而ρx2x3的变化对β影响较小,故而在工程设计中对变量x6,x7之间的相关性需要格外注意.
5 结 论
本文基于增广乘子法和免疫算法提出了一种混合可靠性分析方法,采用增广乘子法构建可靠性优化设计数学模型,从而避免了初始罚因子的选择对计算结果的影响,利用免疫算法对模型进行计算,解决了FOSM法对强非线性极限状态方程的求解难题,为处理实际可靠性工程问题提供了另一种途径.通过数值算例和工程算例对本文算法进行验证,结果表明:本文方法具有良好的收敛性和较好的精度;对线性和非线性问题具有良好的效果,适应性强;并考虑了参数相关性对可靠性指标的影响,对实际可靠性工程问题有一定的指导意义.
