二维复合压电型表面波声子晶体带隙特性

陈长红， 田 苗， 孙美景

(兰州交通大学 数理学院， 兰州 730070)

空间上具有不同周期性的声子晶体[1-2](phononic crystals,PC)由于在传输谱上具有良好的禁带特性，引起了人们的关注。但大量研究主要集中于PC中体波的特性[3-4]，对半无限基底PC中声表面波(surface acoustic waves，SAW)带隙的研究处于初期[5-7]。实际上，SAW带隙可以用于对声能进行过滤、限制或引导等[8-10]，因此将具有不同频段SAW带隙的PC引入到各种设备中可以一定程度的改善其声学性能，如基于PC的SAW滤波器。

为调节SAW带隙，需要寻找合理的PC材料和结构以达到目的。通过改变PC中单元的材料参数、几何参数、晶格形式等[11-14]，带隙频率会被调制。Benchabane等[15]研究了二维正方压电PC中SAW传播，实验和理论上兼证明了SAW完全带隙的存在。Sun等[16]采用有限元法计算了圆锥型PC中SAW的带隙特性并研究了SAW的各向异性传播。Hsu等[17]实验上利用倒圆锥体模型呈蜂窝状排列在压电基底表面上，通过加大倒圆锥的质量来降低SAW局域共振带隙。Tanaka等[18]理论上研究了二维三角晶格PC中SAW与体波的带隙分布，并利用平面波展开法解释了SAW和伪声表面波的能带结构。Achaoui等[19]研究了圆柱成三角晶格、蜂窝状晶格、随机排列PC的SAW传播特性，得出低频局域共振带隙与柱体的晶格形式无关，但Bragg带隙在随机排列中消失。Yudistira等[20]仿真了二维蜂窝状压电空洞型PC在不同方向的非辐射完全SAW带隙特性，并讨论了空洞几何参数对带隙的影响。Ash等[21]在压电基底表面蚀刻有限深度环形孔洞型PC，通过模拟和实验验证了该模型能够产生高衰减低频SAW带隙的结论。最近，Coffy等[22]实验和采用有限元法仿真同时证明了在一维PC中存在一个相对带宽达94%的宽大Lame波带隙，原因是在PC中引入了超薄环氧树脂造成。受此启发，目前无论是数值模拟还是实验研究，在二维压电型声子晶体中添加环氧树脂来研究其SAW带隙特性的相关文献还很少。

为此，本文提出一种微米级尺度的复合型PC，复合柱体以正方晶格的形式排布在半无限压电基底表面。该结构能够有效的降低SAW完全带隙，扩宽XM方向带隙。首先，给出了模型的几何图、及精度高、适应于复杂PC能带结构计算的有限元法理论；计算传输损失的模型及方法。其次，主要讨论了复合型PC的带隙特性，并结合模态分析进一步研究了带隙的形成机理。通过计算传输损耗，讨论了其传输特性。最后，通过改变散射体的几何参数来调节带隙。与传统纯柱型PC相比，新设计的PC在其体积及质量几乎不变的情况下即可有效调制禁带。

1 物理模型及计算方法

1.1 能带结构的计算模型及方法

图1(a)为复合型PC的原胞图、正方晶格排列的俯视图，原胞中柱体由不同材料的底部和顶部组成，沉积在一个半无限压电基底上。晶格常数为a，柱体的半径为r，顶部和底部柱体高度分别为hc和hb。图1(b)为正方晶格的简约布里渊区(BZ)。原胞柱体顶部是金属材料镍Ni，底部是弹性材料环氧树脂(epoxy)，基底为强压电YX-128°LiNbO3材料。参数如表1、表2所示。

基于有限元法来求解声子晶体中声波的机电耦合方程

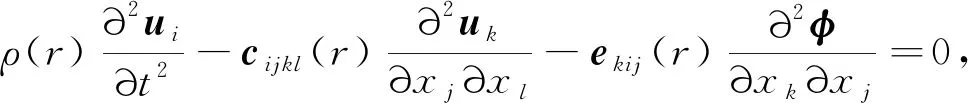
(i,j,k,l=1,2,3)

(1)

(2)

式中：u为应变张量;φ为电势张量；cijkl,eikl,εik,ρ分别为刚度张量、压电应力张量、介电张量、密度。由于PC具有周期性，只需计算一个原胞的带隙特性即可。在单胞的四个侧面使用Bloch-Floquet周期性边界条件(periodic boundary condition，PBC)

ui(x+a,y+a)=ui(x,y)exp(-i(kxa+kya))

(3)

式中：i=x,y;kx和ky为Bloch波失。通过扫描简约布里渊区边界的波失k并求解特征值问题，即可获得SAW声子晶体的能带结构和振动模态。

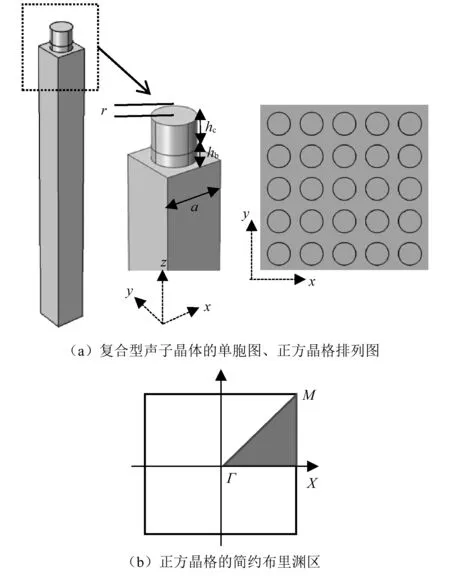
图1 复合声子晶体的三维几何图和正方晶格的简约布里渊区

表1 铌酸锂LiNbO3压电材料与金属镍Ni的参数

表2 环氧树脂的物理参数

1.2 传输损失的计算模型及方法

同样使用有限元法来计算传输损失，为节省计算时间，模型中不考虑空气介质，模型如图2(a)所示。其中设基底高度H=10a，在PC的前段添加线位移激励来模拟矢状面(x,z)线源，该线源能够激发出瑞利波模式。Bloch-Floquet周期性边界条件添加在模型的y轴两侧。为阻止声波在边界发生无必要的反射，x轴两侧及底部添加了完美匹配层(perfect matching layer,PML)。数值计算中，在ΓX方向使用有限个单元胞，用N表示单胞的个数，通过计算入射波在基底左侧表面的位移U0及透射波在基底右侧表面的位移U1来获得传输损失，如式(4)所示。

(4)

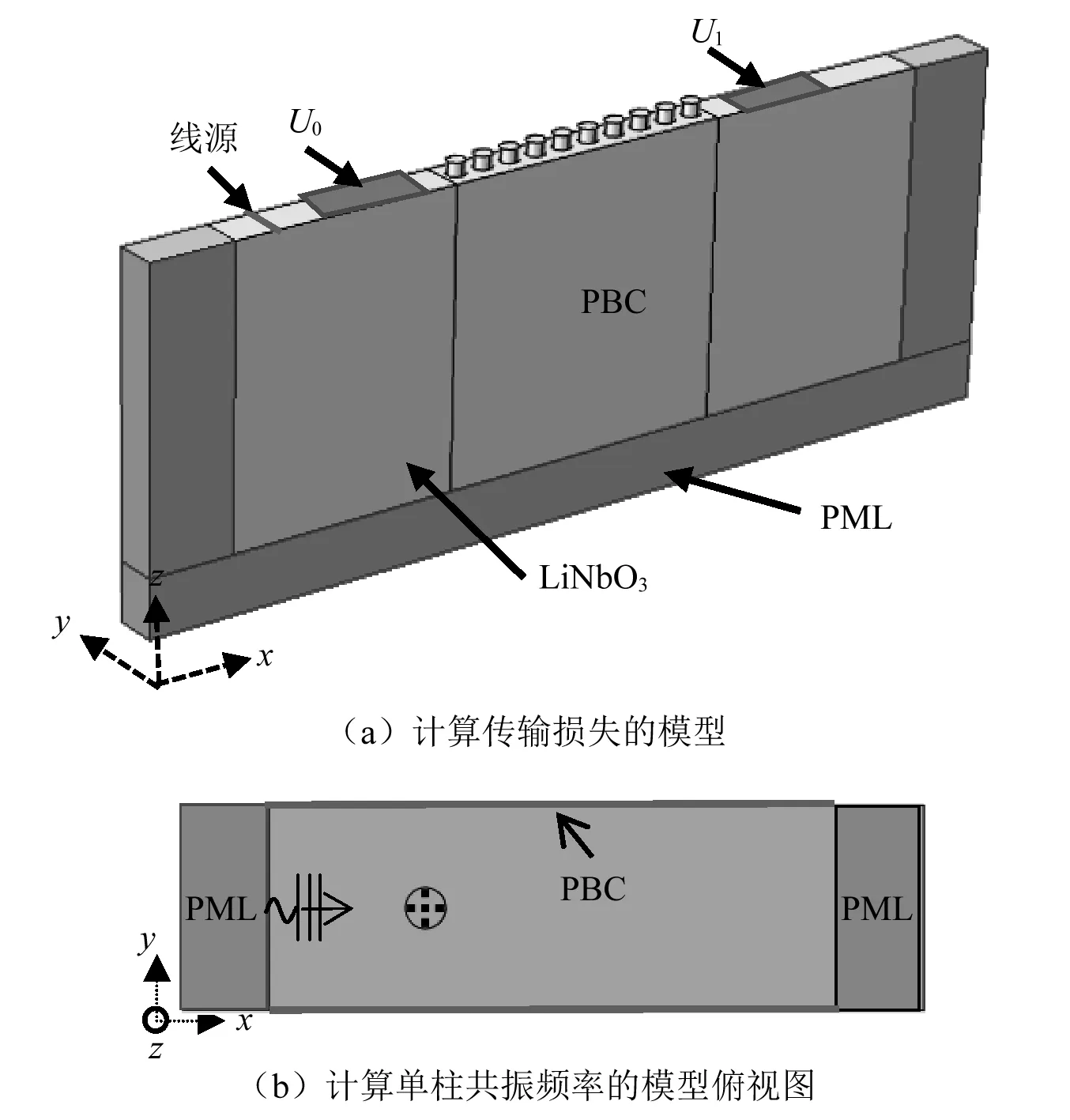
图2 计算传输损耗及复合单柱体共振频率的模型

2 计算结果及讨论

2.1 能带结构

图3(a)、图3(b)为纯镍柱PC的能带结构，图3(c)、图3(d)为复合柱体即镍柱底部有环氧树脂PC的能带结构，灰线为相速度最慢的体波模态用于区分体波和SAW，称为声线。声线以上的灰色区域为辐射带模式即体波，声线以下为非辐射带模式即SAW。通过对比图3(a)与图3(b)，当镍柱体高度hc增加0.15 μm时，能带图中所有的频带都随之降低，第一SAW完全带隙下边界由127 MHz降为122 MHz，但频带降低效果不太明显，仅降低了5 MHz。相似的现象对比图3(c)、图3(d)也能看出。现在，我们来对比图3(a)、图3(c),即顶部柱体hc= 3 μm时，柱底有无epoxy时频带的变化。图3(c)中所有频带明显下降，第一SAW完全带隙由127 MHz变为80 MHz ,变化值为47 MHz，是直接增加顶部柱体高度0.15 μm降低5 MHz的10倍。同样，该现象通过对比图3(b)、图3(d)也能观察到。则通过在柱体底部添加薄epoxy能够造成带隙的有效降低。

下面我们观察复合型PC的振动模态，图4(a)～图4(g)给出了hc= 3 μm,hb= 0.13 μm声子晶体在BZ高对称点X处的振动位移场(图3(c)中已标记)，其中箭头的大小和方向分别表示位移幅值大小和矢量方向。为了更加精确的解释带隙的打开机理，还计算了基底上单个复合柱体的共振频率LR(见图2(b))。模型计算中，在复合单柱的前面应用矢状面(x,z)线源来激发瑞利波。PML和PBC都被用来防止x轴和y轴侧面边界的反射。同时，为了防止复合柱体之间的相互作用，将基底宽设为5a。通过记录柱体顶部五个点的位移分布，能够获得位移峰值即为单个复合柱体的共振频率，为了方便分析，将获得的共振频率用水平线绘制于图3(c)中。

从图4(a)、图4(b)看出，这两个模态分别沿ΓX,XM方向作一阶弯曲振动。从图3(c)发现，单柱的共振频率LR出现在前两个频带附近,且在PC中发生了一种典型的模式排斥行为：LR将能带结构中两条最低的频带分支开。由于一阶弯曲振动在BZ边缘X处的主导作用，第一和第二频带形成与LR紧密结合的弱色散平坦频带。仔细检查发现，第一个分支低于LR，与文献[23-24]相同，但由于一阶弯曲振荡的极化对称性，第二个分支克服了LR。同时，Graczykowski等表明，柱体的一阶弯曲振动与基板中的瑞利模式相位相同。LR之上第三条频带的起始频率从声线处离开辐射区，此时柱体的一阶弯曲振动与基底中瑞利模式相位相反。因此，在80～93 MHz频段内打开了第一条SAW完全带隙即局域共振带隙，这比布拉格带隙要低得多，后者的中心频率由f=c1/2a定义(c1=3 978.2 m/s)，即198.9 MHz。模态c为柱体内的扭转振动(见图4(c)),该模态与基底之间不会发生耦合，从而该模态对带隙的位置没有任何影响。

从图4(d)看出,此模态表现为柱体的上下拉压式一阶振动，但在图3(c)d处并无单柱的共振频率。实际上，基底中的瑞利波与此模态发生了相互作用导致群速度减慢，但它不会产生类似于LR的平直带。因此，在155～186 MHz频率范围内打开的第二条SAW完全带隙，应归为Bragg散射机理，但柱体的上下拉压式振动也是有一定贡献。图4(e)、图4(f)模态在ΓX、XM方向上显示出了柱体的二阶弯曲振动，图3(c)中e、f处也无单柱的共振频率，因此在183～204 MHz频段内第三条SAW完全带隙的打开也归为Bragg散射机理，但柱体的二阶弯曲振动也是有一定贡献的。g模态的能量有一部分在柱体内，还有一部分在基底内，深度正好在g本征频率对应的一个波长范围内，即g模态为瑞利波。

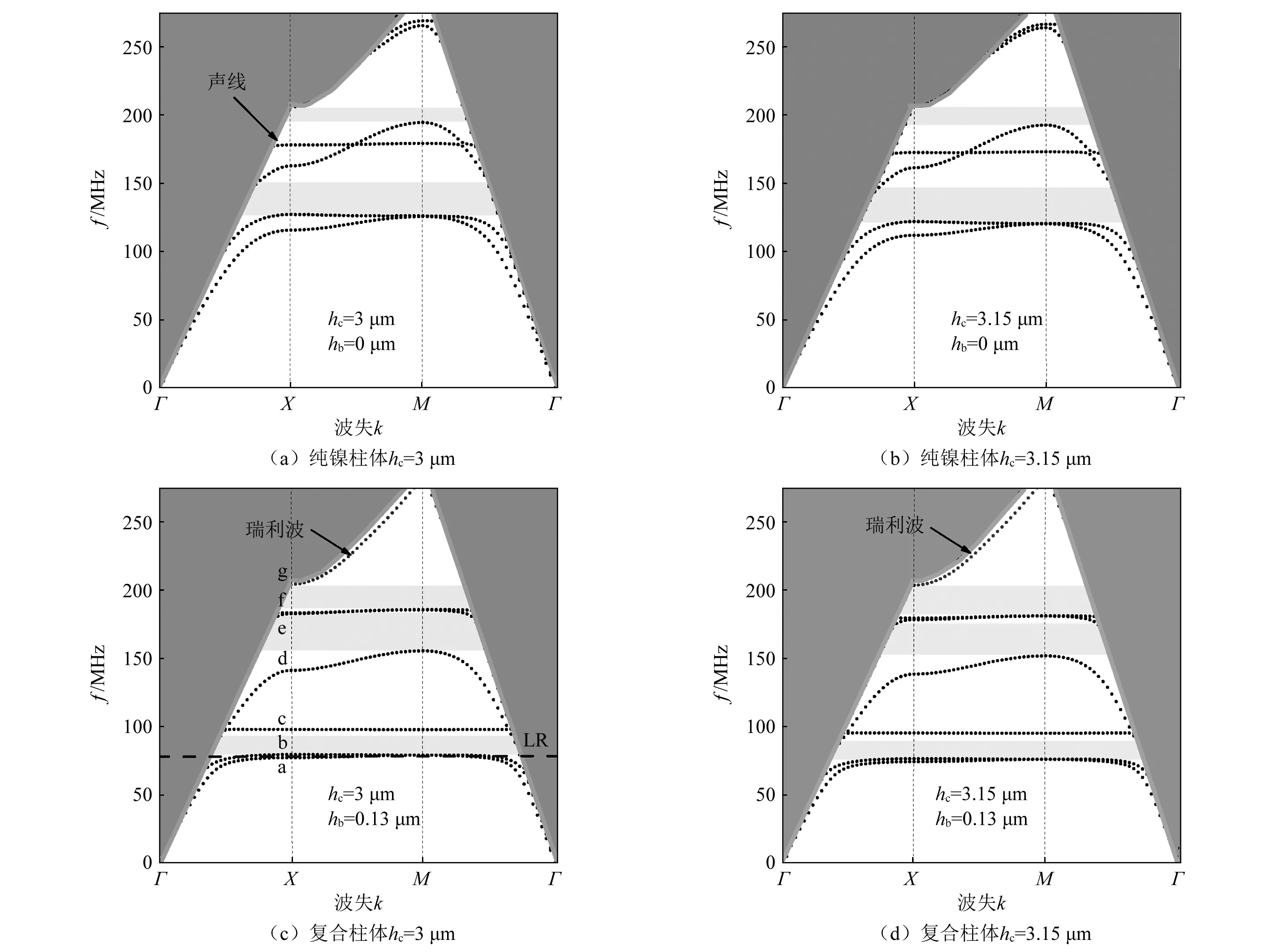
图3 不同尺寸声子晶体能带结构

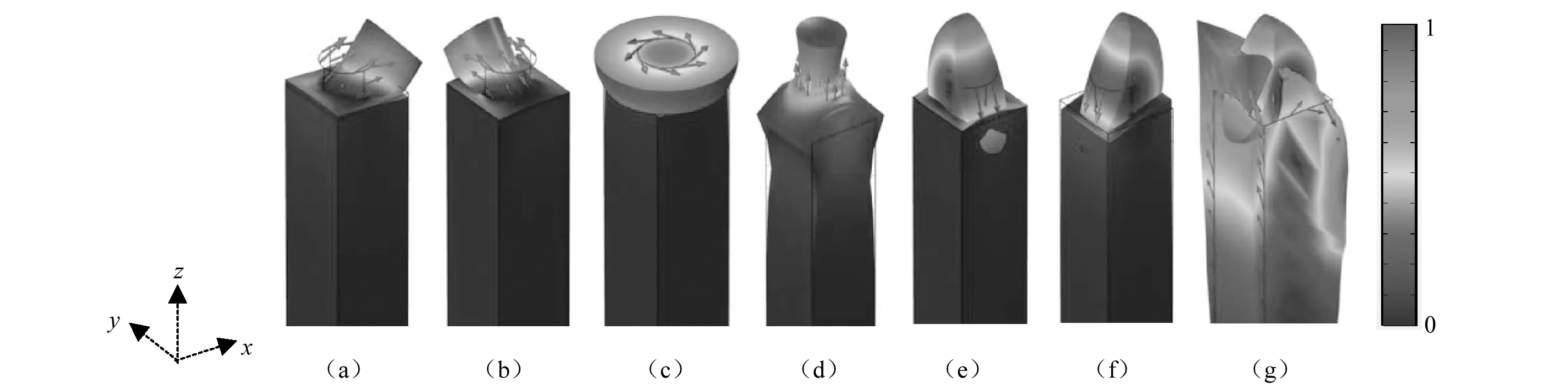
图4 不同本征模态的振动位移场

现在来分析带隙降低的原因，以图3(c)中最低的两条频带为例，根据图4(a)、图4(b)模态，可以把复合单胞看成单自由度质量块—弹簧系统(只考虑拉压刚度)，共振频率的计算公式为

(5)

式中：keff为有效弹性模量，由镍和epoxy共同决定；meff为有效质量，由于epoxy很薄，相对于镍柱的质量非常小(约为0.58%)，因此meff可看成仅由镍柱决定。

keff可认为是两个不同刚度系数弹簧的串联，如

(6)

式中:ENi，Eepoxy分别为镍和epoxy的杨氏模量；S为两柱体间的接触面积。由于Eepoxy要比ENi小两个数量级且hb也很小，则式(6)简化为

(7)

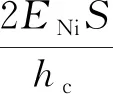
由以上计算分析，推断可使用弹性模量更小的材料来替换epoxy，从而使能带结构产生更明显的变化。但这将会使基底与柱体之间的耦合减小，将会大大的减小控制SAW的效率。

2.2 传输损失的计算

图5(a)为纯镍柱PC沿ΓX方向的传输损失，N=10。由图可得：当hc=3 μm (圆点线)时，在三段衰减区域120～150 MHz, 163～179 MHz, 180～204 MHz中出现了三个低谷(T<-22.5 dB)，分别为130 MHz，169 MHz，180 MHz。与图3(a)ΓX方向的带隙结果保持一致。且注意到第一个衰减谷低于第三个衰减谷，正如图4中的a、b振动矢量场所示，第一带隙是由具有高品质因素Q柱体的弯曲振动引起，弹性能不能很好的局域在柱体中；当hc=3.15 μm(方点线)时，同样，出现了三段衰减区域，与图3(b)ΓX方向的带隙结果保持一致。通过对比图5(a)方点线和圆点线，发现方点线的三个衰减谷都低于圆点线的，这与图3(a)、图3(b)显示的带隙频率向低频移动的趋势一样。

图5(b)为复合柱体PC沿ΓX方向的传输损失，N=10。由图显示：当hc=3 μm时(圆点线)，在76～93 MHz频率范围内出现了衰减谷为80 MHz的窄禁带，应归为复合柱体的一阶弯曲振动的高Q值导致，如图3(c)中前两条频带呈平直带；在141～185 MHz频段出了第二条禁带，衰减谷为145 MHz；在183～203 MHz频段内出现了另外一个衰减谷为185 MHz的窄禁带，原因可能是柱体的二阶弯曲振动与基底中传播的Rayleigh波耦合作用减弱，声能量不能被柱体很好的聚集。三个衰减频段与图3(c)中的带隙位置一致。相类似的现象也存在于hc=3.15 μm时(方点线)，相比于圆点线，方点线整体频率都稍向下移动，这与能带结构图3(c)、图3(d)显示的移动趋势也一样。然而，更明显的特征是：对比图5(a)圆点线与图5(b)方点线，当有epoxy时，衰减谷向低频方向有较大的移动，但衰减率都降低。例如，第一禁带的衰减率由-22.5 dB降为-10 dB，这是因为复合柱体与基底之间的耦合作用减弱了。

图5(c)给出了具有不同单胞数目N=0,5,10声子晶体的传输损失(与图3 (c)中ΓX相对应)。可以看出N=0时，振动比较平缓，几乎没有衰减。当N=5时，振动就出现了较为明显的衰减，而当N=10时，三段衰减区已经十分明显了，因此，随周期数的增加，振动衰减逐渐增大。

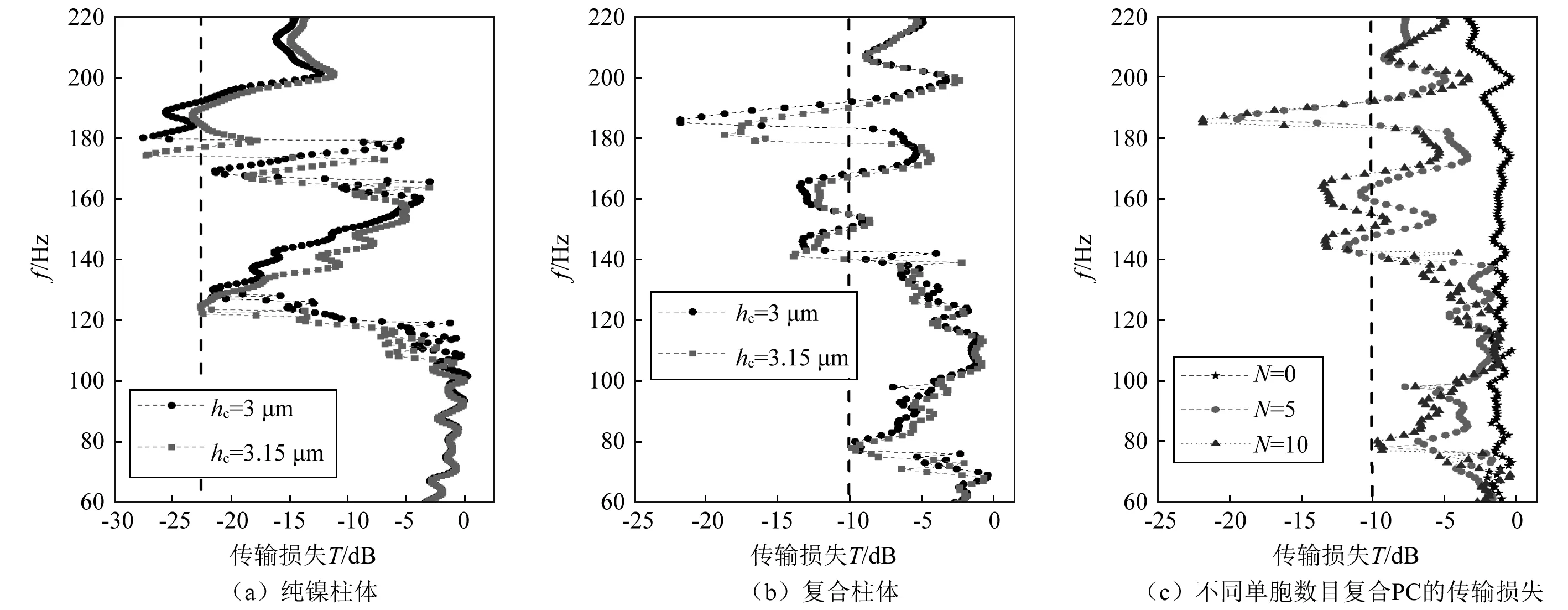
图5 传输损失

经上述分析，发现图5(b)中圆点线的第一衰减区域下边界(76 MHz)稍低于图3(c)中ΓX方向第一带隙起始频率(80 MHz)，方点线类似。为解释该现象图6给出了模式a、模式b不同方向的位移场分量，注意，所有位移场都使用了相同的刻度。由图可得：模式a的能量主要分布在ux和uz方向，该模态具有矢状面偏振特性，且由于本文采用了能够激发出Rayleigh波的矢状面(x,z)线源来计算传输损失，因此第一条频带表现为通带；模式b能量主要分布在uy和uz方向，在结构的x-z中间面内uz位移场成反对称性，当采用矢状面(x,z)线源时，声能量不能通过该模态传播，从而导致传输损失中第二条频带的缺失。但uy和uz位移场在结构的y-z中间面内具有对称性，该模态能够被剪切水平极化线源激发。

图6 模式a与模式b不同方向的振动位移场

2.3 柱体半径对带隙的影响

图7(a)为保持hc= 3 μm，hb=0.13 μm不变，柱体半径r变化时对SAW完全带隙影响。随着r的增加第1 完全带隙的起始、截止频率都移向高频，宽度逐渐拓宽。第2 完全带隙的起始、截止频率都移向低频，但宽度先变大再减小，最大带宽为24 MHz。第3 完全带隙的宽度先持续扩宽直至定值。

通过观察图3(c)、图3(d)中XM方向带隙，发现该方向存在较宽的带隙，因此，我们还研究了r变化时XM方向带隙的变化。如图7(b)所示，第1带隙的截止频率与第2带隙的起始频率共频带，且该频带基本保持平直带，从而形成了一条宽大带隙，带宽随r的减小逐渐扩宽，当r=1.0 μm时，带宽达到了123 MHz。第3XM方向带隙的宽度则是先变宽再逐渐变窄。第4XM方向带隙的宽度则在小于r=2.5 μm时存在但很窄，大于r=2.5 μm时带隙宽度缓慢扩宽。

2.4 环氧树脂厚度对带隙的影响

图8(a)为保持hc=3 μm,r=3.2 μm不变，epoxy厚度hb增加时SAW完全带隙的变化图，随着hb的增加所有禁带的起始、截止频率都向低频域移动。第1完全带隙宽度逐渐减小，直到hb=0.5 μm后带宽基本保持不变。第2完全带隙(即频段最窄的带隙)宽度被逐渐压缩，最终会消失，PC只会存在两条带隙，即原来的共振系统被破坏，带隙由原来的三条压缩成为两条，因此为了得到较多的完全带隙，hb的值不能太厚。第3完全带隙的宽度先增加后逐渐减小，最大带宽出现在hb=0.3 μm，带隙最大值为40 MHz。

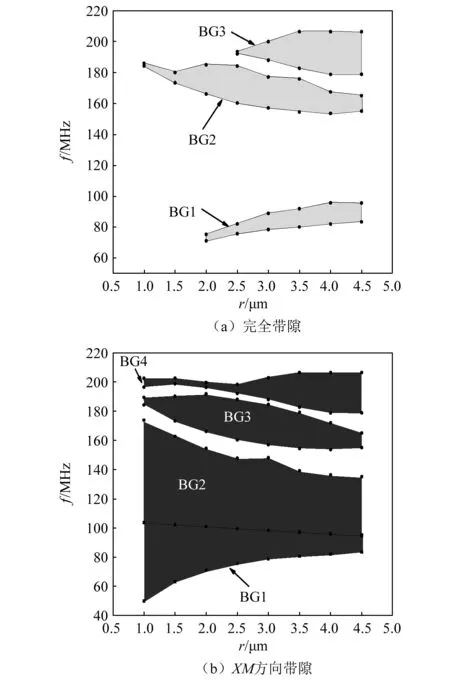
图7 柱体半径r对带隙的影响

图8(b)为hb增加时SAW沿XM方向带隙的变化图，该方向有4条带隙，第 1、第 2、第 3 带隙的起始、截止频率都移向低频，且带宽都是先逐渐减小，直到hb=0.4 μm时基本保持不变。第4带隙起始频率移向低频，截止频率基本不变，因此带宽明显逐渐拓宽，当hb=0.8 μm时，带宽高达100 MHz。同时，随着hb的增加第2与第3带隙之间的通带逐渐减小。当hb=0.7 μm时，4条方向带隙将会发生融合，产生一个带宽为158 MHz的宽大带隙。

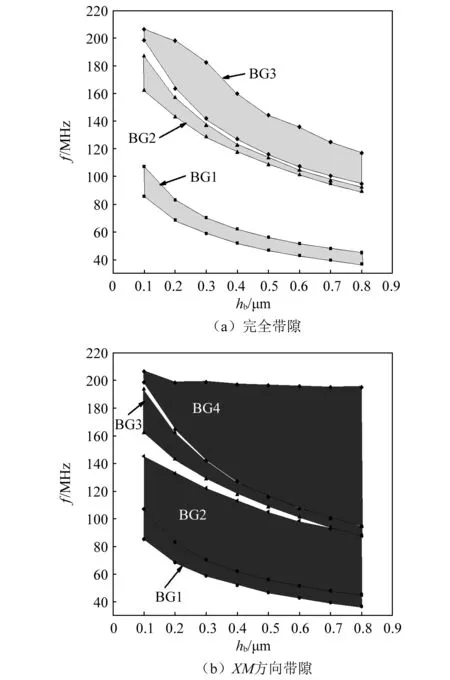
图8 环氧树脂厚度hb对带隙的影响

3 结 论

本文设计了一种在镍柱体底部增添薄epoxy并沉积在铌酸锂基底的二维复合压电型PC。基于有限元法计算了能带结构、传输损失及振动位移场。结果表明，通过在共振体中引入epoxy来减小其有效弹性模量，即可有效降低SAW完全带隙；同时，在30～225 MHz频段内打开了多条XM方向带隙；通过振动模态分析了带隙的形成机理，得除第1带隙为局域共振外，其余为Bragg带隙。通过分析传输特性显示，复合型PC的透射率低于纯柱体型PC的，起因是共振体与基底之间的耦合减小。最后，研究了散射体几何参数对SAW带隙特性的影响。结果表明，共振体半径越大、环氧树脂厚度越小，第一SAW完全带隙宽度越宽；同时，随epoxy厚度的增加，XM方向数条带隙将会融合成一条宽为158 MHz的宽大带隙。研究结果为调控微米尺度声子晶体的SAW带隙特性提供了可靠的理论依据。也为微型结构的设计提供了崭新思路。同时，为设计高性能声学器件提供一定参考。