极端工况下的高压柱塞马达密封环摩擦特性

张乐涛， 刘志奇， 董洪全， 李占龙， 徐 彦

(太原科技大学 机械工程学院，太原 030024)

为适应机械设备大型化的发展趋势，以及高速重载、不稳定的极端工况，提高系统可靠性显得尤为重要。柱塞马达是液压系统中重要的动力执行装置，其中斜轴结构相比于传统的斜盘结构有更大的输出排量，和更高的机械效率[1]。斜轴马达的密封装置密封环工况环境复杂，在交变摩擦应力的作用下易发生疲劳断裂，导致马达容积效率下降[2]；而合理地设计密封环结构可达到减摩效果。

磨损是导致密封环断裂失效和马达泄露的重要因素之一。磨损的过程是多物理场耦合的结果，其中接触比压过大导致了摩擦副的磨损。Jung等[3-4]研究得出负载增加和转速提高会增大油膜的黏性摩擦力，进而增加密封环的摩擦力。Tomanik等[5]发现密封环与环槽的长期碰撞使表面基体逐渐剥落，基体对密封环表面造成磨损并产生微裂纹，裂纹的扩张导致密封环的断裂。毛淑芳等[6]对柱塞副进行磨损研究，指出法向正压力是影响柱塞副磨损的重要因素。Bartelt[7]仿真分析摩擦副的配合间隙对磨损的影响，得出减小配合间隙可以改善磨损。

优化结构参数可以减少密封环的摩擦磨损，增强结构强度并提升使用寿命。王政等[8]计算了多种型面对活塞环摩擦磨损的影响，研究发现中凸结构磨损最小。Shibuga等[9]试验研究型面结构对摩擦磨损的影响，结果表明优化后的型面摩擦磨损降低了10%。Robinson等[10]通过增加环岸高度可以减小活塞环与环槽之间的接触应力，提升活塞环的强度并减少磨损。Manring等[11-12]试验研究了滑靴副结构参数对油膜流场的影响，得出油膜的压力与斜盘壁面剪切应力的分布。

通过模态分析方法对柔性构件进行离散化，并建立刚柔耦合模型进行精确的动力学分析，是对多体系统动力学分析的主要方法[13]，再使用有限体积法进一步分析结构变化对流场流体动力学的影响，综合分析结构对密封环摩擦性能的影响[14-15]。本文以柱塞马达密封环为研究对象，基于Kane方程建立柱塞马达数学模型和物理模型，并使用有限体积法对流场区域离散建立流场模型，在Fluent中计算动压和壁面剪切应力，分析不同结构参数下密封环的摩擦特性。研究结果将为高性能密封环的设计提供理论基础和依据。

1 马达刚-柔耦合多体系统建模

1.1 多刚体系统建模

柱塞马达系统机构简图，如图1所示，极端工况下的马达工作原理为：进出油口的高低压油流经配流盘和缸孔作用在柱塞尾部，压力差产生力偶推动主轴旋转并输出扭矩。图1中:P为吸油区的高压油;T为马达输出的扭矩。

图1 高压柱塞马达机构简图

1.2 柔性构件的离散

高速高压的极端工况下，密封环的弹性振动不可忽略，通过有限元方法将其离散为形状规则的六面体单元，把密封环看成柔性体，并考虑其变形量,如图2所示。将其他部件作为刚性体，对刚体运动和柔性体的弹性变形进行耦合分析。

图2 密封环柔性构件的离散

1.3 密封环运动学分析

密封环的运动形式包含吸排运动，挤压运动和摆动运动三种形式。吸排运动是使密封环沿轴向做正弦往复运动以完成马达的进出油。挤压运动为密封环沿径向对油膜的周期挤压。摆动运动为圆台型柱塞驱动与随动两种状态交替下的摆动运动。

吸排密封环正弦往复运动规律

vx=ωRgsinφtanγ

(1)

式中:vx为密封环的轴向运动速度;ω为缸体旋转角速度；Rg为缸体分度圆半径;φ为主轴绕轴线转动的角度;γ为主轴转角。

由图3建立多体系统控制方程，其中密封环任意一点P相对于Kane方程下系统坐标系OXYZ原点O的矢径

d=q+Ls

(2)

密封环上任意点P的速度

(3)

密封环上任意点P的加速度

(4)

密封环转动角速度矢量δ为

(5)

式中:d为柱塞上P点相对于系统坐标系的矢径;q为柱塞坐标系原点O′相对于系统坐标系原点O的矢径;L为从柱塞坐标系到系统坐标系的坐标变换矩阵;s为点P相对于柱塞坐标系原点O′的矢径。

图3 密封环在惯性系下的运动描述

1.4 密封环动力学分析

依据密封环结构和关键参数，密封环量纲-结构参数取值范围,如表1所示。密封环在极端工况和复合运动下，其受力情况较复杂。密封环受到轴向和径向两个方向的摩擦力，其中径向摩擦力由挤压和摆动运动时密封环与柱塞的相对运动产生，且柱塞对缸孔的冲击引起密封环轴向和径向摩擦力的波动，如图4所示。另外，密封环尾部高压区p1与端部低压区p2形成其与缸孔间的压差流；且密封环的吸排运动使间隙同时具有剪切流，油液与密封环的壁面剪切力影响着摩擦力。

表1 密封环量纲-参数确定

图4 密封环受力分析

ΣFx=0Fp-Fr-(Ff+Fmr)cos Ф=0

(6)

ΣFy=0p-FN+Ffb+Fωrcos Ф-G=0

(7)

式中:Ffb为密封环与柱塞之间的摩擦力;Fr为密封环与柱塞之间的正压力;Ff密封环与缸孔之间的摩擦力;Fp为作用在密封环上的液压力;p为密封环内油液的压力;FN为密封环与缸孔之间的法向正压力;Fωr为密封环的离心力;Fmr为密封环的惯性力;α为密封环弧面锥角;Ф为柱塞的摆动角度。

引入系统广义混合坐标：柔体弹性变形坐标和刚体运动坐标，并采用模态分析法，通过模态坐标表示系统的物理坐标

dk=ρψk

(8)

式中:dk为k点相对于相对位移向量在系统坐标系中的列向量;ρ为模态向量矩阵;ψk为k点的模态坐标向量，其导数为广义速率，对任意点速度v关于广义速率取偏导数，得偏速度矢量vk′。

两个密封环相对于广义速率的惯性力

(9)

两个密封环相对于广义速率的离心力

(10)

密封环重力对应的广义主动力为

(11)

式中:m为密封环的质量;v1′为密封环1的偏速度矢量;v2′为密封环2的偏速度矢量;a1为密封环1的质心加速度;a2为密封环2的质心加速度。

1.5 柱塞副冲击对密封环摩擦特性的影响

图5 冲击对密封环摩擦特性的影响

从图5可知，斜轴马达的柱塞在驱动缸体时存在摆动，高转速下对缸体造成冲击并改变柱塞副原有的平衡，则柱塞副中的密封环法向正压力发生变化并较冲击前增大。密封环摆动过程中始终与缸孔接触，正压力增大导致其弹性变形增大，则实际接触面积增大摩擦力增大，同时变形使摆动支点前移L3并对密封环支撑力为FФ，形成滚动阻力矩M(M=FФ1·L3)和滚动静摩擦力FФ2。

柱塞副受力平衡方程

ΣFx=0FN3cos Ф+Ff1+Ff2+Fmg-Fp=0

(12)

(13)

由式(13)得密封环滑动摩擦力

(14)

根据弹流润滑理论，密封环与缸体间润滑按全膜弹流润滑计算，则密封环摩擦因数f

(15)

式中:分子为密封环壁面的黏性摩擦力；分母为密封环油膜压力；x1，x2分别为密封环油膜润滑区域起点和终点横坐标；d1为密封环外径；τ为密封环壁面剪切应力；p′为密封环壁面单位面积油膜压力。摩擦因数随接触状态和相对滑移速度变化而变化，而法向正压力由密封环弹性力和阻尼力组成，其表达式为

(16)

式中：k为密封环材料Hertz接触刚度，经查表取105N/mm；δ为接触渗透深度；e为力指数取1.5；STEP为阶跃函数；dmax为接触区最大穿透深度，取值0.1 mm；cmax为最大穿透量下的阻力值，取值50 N·s/mm。

2 密封环-缸孔流场建模

密封环的润滑形式为弹性流体动力润滑(elastohydrodynamic lubrication，EHL)，为进一步分析极端工况下密封环的流场摩擦特性，利用图6模型在Fluent中计算动压力和壁面剪切应力。计算模型为不可压缩流体，使用三维不可压缩N-S方程，由于密封环缝隙油膜水力直径较小，故其流动为层流运动，而缸孔内雷诺数Re=6 000，由Re>Rec可知缸孔内为湍流并为均匀湍流，故选择湍流模型为标准k-ε模型，入口和出口均设置为压力边界，分别为35 MPa和0.1 MPa。

图6 模型各截面及边界条件

整个计算区域网格划分均采用六面体结构化网格，如图7所示。为得到密封环壁面平均剪切应力变化，对其壁面进行网格加密以提高计算精度，如图7(b)二维轴切面壁面处共设置680个节点，并确保油膜最薄处有6层网格。本文使用动网格技术实现密封环的运动，通过编译用户自定义函数(user-defined fuction, UDF)控制密封环的复合运动，因网格为六面体单元且变化方向与速度一致，故动网格采用Laying方法实现网格的拉伸与压缩(其他方法不适用六面体单元)，缸孔壁面设置为Deforming，柱塞和密封环设置为Moving Body。各项残差均设置为1×10-6，计算6个周期，计算设置每时间步长最大迭代次数为60次。

图8为计算区域网格无关性验证，分别计算网格数为478 768，622 398及833 597六面体结构化网格0.03 s时密封环壁面动压分布，结果表明网格数量的变化对动压计算结果影响较小。综合考虑计算精度和效率，选用622 398网格数量的计算模型。

图7 计算区域及局部网格分布

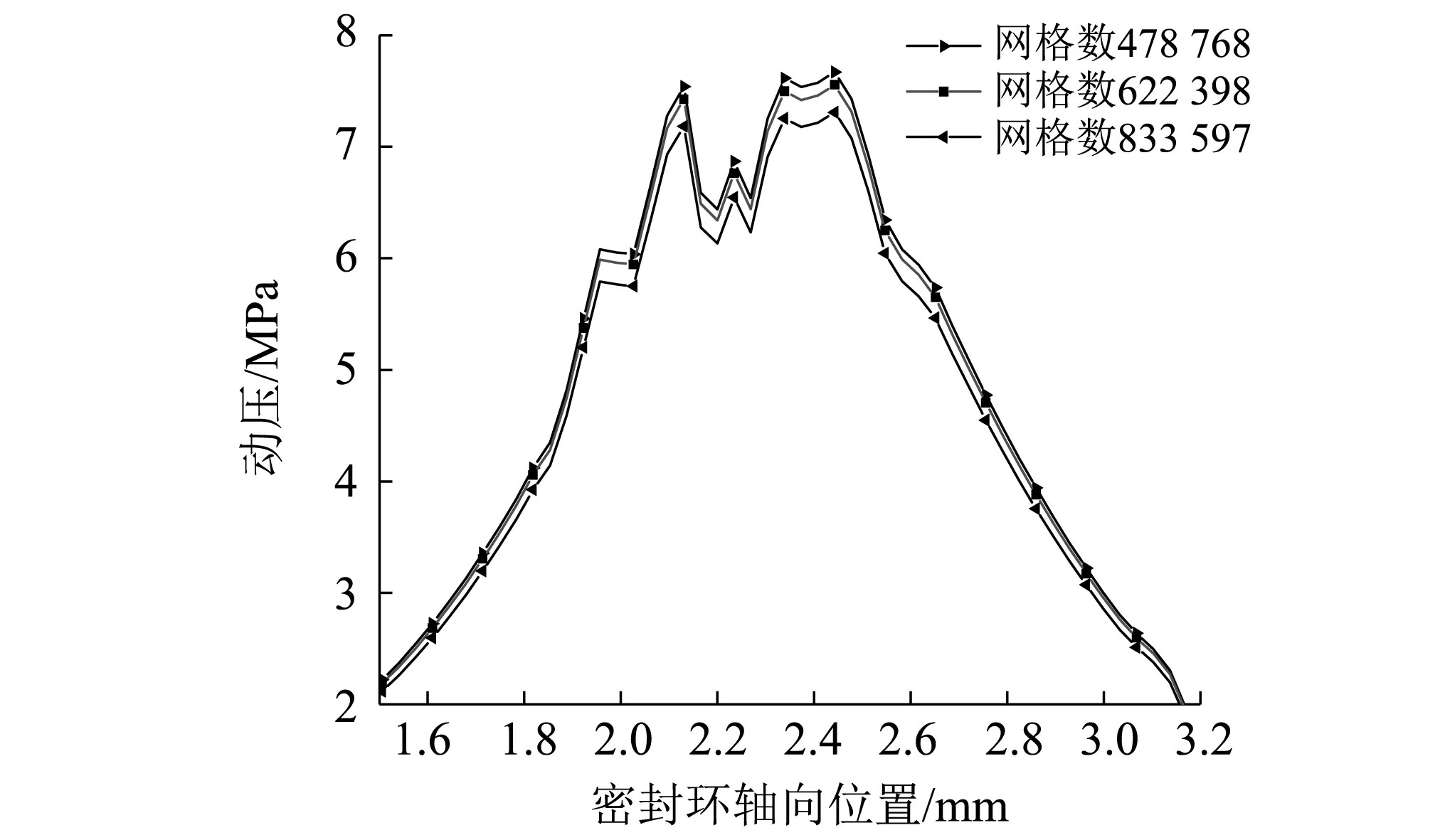
图8 网格无关性验证

缸体压力出口单位面积上的剪切应力为τ

(17)

式中:μ为流体间内摩擦因数(黏滞系数)；du/dy为速度梯度，剪切应力受结构参数影响，所以结构的改变会影响剪切应力的大小。

密封环壁面的黏性摩擦力

F=τπd1d2

(18)

式中：d1为密封环外径；d2为密封环宽度。当直径和宽度为定值时，缸孔壁面摩擦力和壁面剪切应力呈正比，则摩擦力受到型面形状的影响。故流场分析以壁面剪切应力线性表示壁面摩擦力。

3 动态响应计算及仿真

3.1 材料选取和边界条件设置

通常额定工况(T=800 N·m)下密封环的摩擦磨损较小，而在极端工况(T=900 N·m)的场合下，超载和连续作业会加剧密封环的磨损直至断裂失效。现选择材料为结构钢，密度为7 801 kg/m3，弹性模量为2.07×1011N/m2，泊松比0.29，密封环质量4×10-3kg；进出口压差ΔP=34.9 MPa，负载为900 N·m。另极端工况下相关技术参数,如表2所示。

表2 马达的工作参数

参照表2所示的极端工况，并添加表3的约束关系，对密封环进行柔性仿真。首先利用软件ANSYS将密封环进行离散实现柔性化，然后在软件ADAMS导入柔性体，设置相关边界条件并进行动态响应求解。

表3 马达在ADAMS里的约束关系

3.2 数值计算及验证

为验证所选数值方法的准确性，同极端工况下将ADAMS和式(3)Kane方程所建模型的软件MATLAB计算结果相比,图9所示密封环的速度基本一致，误差小于3%，误差主要源于MATLAB没有考虑摩擦力的突变，故速度计算结果较ADAMS计算值偏大；并将Fluent的计算值与Cho等[16-17]的计算值进行对比，结果如图10所示。计算值较试验值有偏差，平均偏差3.9%，这是因为压力脉动，传感器误差和油液黏度等参数综合影响结果，但所建模型和试验结果整体基本吻合，对力特性曲线的局部细节变化趋势预测一致，因此所选数值方法可以有效模拟马达的极端工况。

图9 密封环轴向速度对比

图10 密封环壁面剪切应力对比

3.3 两个密封环的受力对比

机构冲击特性对密封环摩擦阻力变化有重要影响。密封环径向摩擦力Ffb如图11和图12所示。代入密封环质量参数和工况条件，由式(6)、式(7)计算得到的摩擦力Ffb只有492 N。但由于马达高速旋转下接触时间的减少，冲击过快引起法向正压力的突变，进而导致摩擦力的增加，其平均值为490 N，最大值为613 N，则实际受到的摩擦力大于理论上的摩擦力，对密封环造成不利的影响。相比于密封环1，密封环2环槽径向摩擦力受到转角差的影响较小，导致法向正压力小于环1，而摩擦力与法向正压力成正比，其平均值为302 N，幅值为512 N，所以环2摩擦力小于环1。

图11 密封环1与柱塞的摩擦力

图12 密封环2与柱塞的摩擦力

图13为密封环与缸孔之间的轴向摩擦力Ff，与径向摩擦力变化规律相同，环1受冲击影响大于环2，结果显示环1的平均摩擦力为623 N，环2的平均摩擦力为335 N，所以密封环1轴向摩擦力大于密封环2。相比于密封环与缸孔的摩擦力，其与柱塞的摩擦力较小，因此密封环的轴向摩擦力是其摩擦磨损主要因素之一。

图13 密封环与缸孔的摩擦力对比

4 结构参数对密封环摩擦性能的影响

结构参数的改变会引起密封环的质量，惯性力，刚度和强度的变化，引起密封环相关动态性能的改变，并影响密封环的摩擦磨损。在极端工况下，选取设计经验值范围内5个数值，针对不同的宽径比和弧面锥角对密封环摩擦性能的影响进行动态响应计算。

4.1 主轴转角对密封环摩擦性能的影响

选取主轴转角θ=21°～25°，随着主轴转角的增加，密封环受到的摩擦力有所减小，但变化程度并不明显，所以仅从改变主轴转角来减少摩擦磨损意义不大，如图14所示。

4.2 宽径比和弧面锥角对摩擦性能的影响

4.2.1 宽径比对密封环摩擦性能的影响

柱塞圆台型结构导致马达工作时存在转角差，柱塞与缸孔间歇接触且冲击导致冲击力突变，故密封环的法向正压力大小随之出现波动和突变，接触比压的变化引起弹性变形量的变化，变形越大实际接触面积越大则摩擦力越大。如图15和图16所示,当d2/d1=0.20时，法向正压力幅值和应力幅较大，这是因为厚度较小时，机构运动不平稳密封环摆动运动较剧烈，摆角Ф出现大幅波动致法向正压力幅值较大，且弹性变形对密封环的摩擦特性影响较大，厚度较小形变较大引起密封环摩擦力幅值过大；当d2/d1=0.25～0.30时，随着厚度增大形变减小，摆角波动减小致法向正压力应力幅呈减小趋势，则密封环弹性力下降形变减小，摆动对密封环的摩擦影响逐渐减弱，在d2/d1=0.30时摩擦副间的法向正压力达到最小；当d2/d1=0.30～0.40时，当厚度进一步增大时，密封环离心力的增大与机构的卡顿使法向正压力再次增大，当d2/d1=0.40时法向正压力达到最大值。由图15可知，摩擦力变化趋势与法向正压力正相关，当d2/d1=0.30时，密封环受到的摩擦力达到最小，其摩擦力最大减少率为28%。

图14 主轴转角对密封环摩擦力的影响

图15 宽径比对法向正压力的影响

图16 宽径比对摩擦力的影响

4.2.2 弧面锥角对密封环摩擦性能的影响

为避免柱塞拨动缸体时机构出现卡死并减小摩擦力，将密封环型面加工成弧面形状，密封环通过弧面与缸孔接触，密封环自身的摆动随着柱塞摆角的变化而变化，故型面曲线会对摆动运动平稳性造成影响，进而引起法向正压力和摩擦力的改变。不同弧面锥角下密封环摆动运动加速度发生改变，因此选择合适的弧面锥角有利于改善密封环的受力状态。当α=1.6°～1.8°时，随着弧面锥角的增大，摆动运动较为稳定，故加速度和法向正压力逐渐减小，在α=1.8°时达到最小，此时密封环受力状态最佳；当α=1.8°～2.0°时，摆动运动平稳性变差，而加速度和法向正压力再次增大。摩擦副之间的摩擦力应力幅在α=1.8°时最小，密封环摩擦力最大减少率为25%,如图17和图18所示。当前对密封环型面设计尚无设计规范，结果为设计提供参考。

图17 弧面锥角对法向正压力的影响

图18 弧面锥角对摩擦力的影响

4.3 结构参数对壁面剪切应力的影响

缝隙油膜流动分为压差流和剪切流，形成原因为进出口压差和壁面相对运动。图19为t=0.01～0.03 s不同时刻下密封环的流场压力分布，随着密封环的复合运动，对比图19(b)和图19(d)可知油膜压力受挤压和剪切作用出现周期性变化，而密封环油膜沿轴向压力分布规律保持一致，沿轴向方向呈递减趋势。另壁面剪切应力分布规律为先增大后减小，且壁面剪切应力与速度梯度成正比，其大小主要受到密封环速度分布和型面结构的影响。因此，从结构角度出发，合理设计密封环型面参数可以提高油膜动压和厚度，改善润滑并有效的降低壁面剪切应力，进而降低密封环摩擦力。

仿真分析密封环型面对流体内摩擦力的影响，得到结构参数对剪切应力的改变程度，完成密封环减摩的设计。图20得出宽径比对于壁面剪切应力影响较大，当d2/d1=0.2～0.4时，随着宽径比的增大，剪切应力持续增大，这是由于随着密封环厚度的增加，导致油液润滑区域也随之增大，进而引起缸孔壁面剪切应力的增大，剪切应力的增大会加剧密封环的摩擦磨损。图21为弧面锥角对剪切应力的影响，锥角对油液的速度分布影响较小，当α=1.8°～2.0°时，随着锥角的增加，最大剪切应力变化较小，仅在前端和尾部有小幅增大，其最大增幅为0.05 MPa，因此弧面锥角对于壁面剪切应力影响程度较小，也对密封环摩擦力影响较小。

图19 不同时刻流场局部的压力分布

图20 宽径比对壁面剪切应力的影响

图21 弧面锥角对壁面剪切应力的影响

5 结 论

(1)对极端工况下的密封环进行离散柔性化提高了计算精度，并结合Kane方程对柱塞马达进行建模，可以得出结构参数改变对密封环摩擦性能有显著影响，也为其性能的优化设计奠定了理论基础。

(2)主轴转角的变化对于密封环的摩擦性能影响较小，而密封环结构参数对于摩擦性能影响较大，当宽径比d2/d1=0.25～0.30时，随着宽径比的增加，摩擦力逐渐减少，平均摩擦力在d2/d1=0.30时最小;当d2/d1=0.30～0.40时，宽径比进一步增加，摩擦阻力又出现增长趋势，最大减少率为28%。当α=1.6°～2.0°时，随着弧面锥角的增大，摩擦力先减小后增大，在弧面锥角为α=1.8°时，密封环与缸孔的法向正压力应力幅最小，最大缩减率达到25%，此时密封环磨损程度最小。

(3)结构参数的变化也会引起壁面剪切应力的变化。随着宽径比的增加，润滑区域持续增大，剪切应力逐渐增大，摩擦力随之增大。而弧面锥角对于壁面速度梯度影响较小，所以对剪切应力和摩擦力的影响程度较小。