基于三元伪随机序列集的多声源房间脉冲响应测量方法∗

许 凡 申雨晨 冯雪磊 沈 勇

(南京大学 近代声学教育部重点实验室 南京 210093)

0 引言

在房间声学领域，诸多情况下需要测量多个声源的房间脉冲响应。例如，在构建房间几何模型的算法中，常会使用多个声源以增加测量精度[1−6]，这就需要对多个声源进行并行测量，以降低测量时间，提高测量准确度。

一方面，扫频信号是声学测量领域一种测量单个声源的传统的测量信号。为了缩短使用扫频信号测量多个声源的时间，Majdak 等[7]提出了多重对数扫频方法(Multiple exponential sweep method,MESM)，将不同声源重放的扫频信号部分重叠以提高测量效率。此后，Dietrich 等[8]降低了该算法非线性分量的相互干扰，进一步缩短了测量时间。MESM 的优点在于，对每个声源而言，其测量信号均相当于是扫频信号，因此测量准确度较高，且不会受到待测声源非线性特性的影响。然而，这种方法将不同声源的重放过程错开，测量时间仍然长于单个扫频信号，且仍可能引入由于各通道不同步而产生的额外误差。

另一方面，二元伪随机序列在声学测量领域得到了极为广泛的应用，如M 序列(Maximum-length sequence)常用于测量扬声器频率响应或者房间脉冲响应[9]。M 序列作为测量信号，最主要的优点是生成方便、计算简单。在计算资源尚不充足的年代发挥了重要的作用[10]。然而，同扫频测量等其他传统的测量方法类似的是，M 序列每次只能测量一个声源，难以满足对于多声源同时测量的需求。

为了缩短使用二元伪随机序列测量多个声源的时间，Xiang 等[11]拓展了传统的二元伪随机序列测量方法，使用互逆M 序列对(Reciprocal maximum-length sequence pairs)同时测量两个声源。但是，由于互逆M序列对的特殊性，将该方法直接推广到多声源时遇到了困难。此后，Xiang 等[12]利用M 序列生成Gold 序列集与Kasami 序列集，其具有类似互逆M 序列对的自相关和互相关性质的特点，成功将该方法推广到多声源情况，实现了多声源同时测量。相比于MESM，使用二元伪随机序列进行测量，所有声源同时重放测量信号，因此总测量时间与单个声源的测量时间相同，测量效率更高。此外，由于所有声源同时测量，该测量方法可以避免由于各通道不同步而引入的额外误差。然而，这种测量方法存在两个缺陷：其一，该方法规定编码信号和解码信号都只能是二元信号；其二，该方法规定编码信号和解码信号完全相同。该方法对于编码信号和解码信号的这两个约束是由Gold 序列集或Kasami序列集的数学性质决定的，但是这两个约束对于声学测量而言并无必要，反而限制了编码信号和解码信号的可选空间，使得序列集的相关特性存在较大的可优化空间。这就导致实际测量中，由于各通道干扰而产生的噪声较大，极大地限制了测量准确度。

为了解决这个问题，本文使用最佳屏蔽零相关域序列偶集(Optimized punctured zero correlation zone sequence-pair set，以下简称OPS)作为编解码序列集[13]。2004年，蒋挺等[14]在研究最佳二进序列的基础上，提出了最佳屏蔽二进序列偶。随后，许蕾等[15]将最佳屏蔽二进序列偶应用于构造零相关域序列集，并提出了构造OPS 信号的方法。此后，OPS 信号被应用于多输入多输出(Multiple-input multiple-output, MIMO)雷达中，用以提高MIMO雷达的距离分辨率[13,16]。相比于Gold 序列集或Kasami 序列集，OPS 信号的解码信号为三元信号，且编码信号和解码信号并不相同，并由此获得了更好的相关特性。

本文第1 节简述了利用Kasami 信号和OPS 信号进行多声源同时测量的原理，以及这两种信号的相关特性和生成方法；第2节通过仿真实验，对比了扫频信号、Kasami 信号和OPS 信号作为测量信号时，脉冲响应测量结果的差异，并研究了声源个数、序列阶数等因素对于测量结果的影响；第3 节通过实验进行验证；第4节为结论。

1 多声源同时测量方法

1.1 测量原理

考虑有p个扬声器，q个传声器，各个声源同时重放测量信号。如图1所示，设si(n)为第i个声源发出的信号，也即该测量系统的编码信号，则第j个传声器接收到的信号rj(n)可表示为

其中，hij(n)表示第i个扬声器到第j个传声器的房间脉冲响应，∗表示线性卷积。

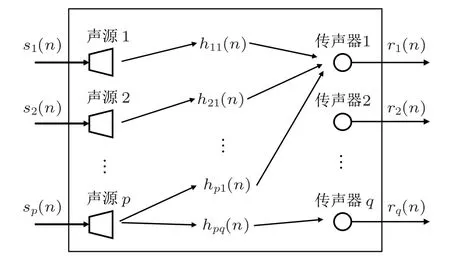
图1 多声源同时测量系统Fig.1 Simultaneous measurements of multisource systems

第k个声源的解码序列vk与接收信号的互相关序列为

这里⊗表示求周期相关函数，定义为

其中，L表示信号长度，i和j表示两个序列在对应序列集的序号，符号AmodB为取模运算，表示A除以B的余数。如果测量信号满足

则可以得到

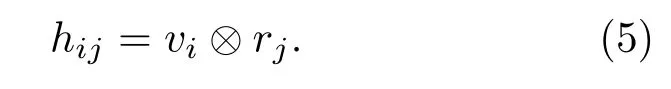
这样即可计算出任意声源到任意传声器的房间脉冲响应。

1.2 Kasami信号的性质和生成方法

由式(4)可知，所需要的测量信号应该满足以下3个条件：(1)每个测量序列的自相关函数都近似脉冲函数；(2)任意两个测量序列的互相关函数近似为0；(3)测量序列的数量足够多，以满足多声源测量的要求。

在数学上，Kasami 序列集可以满足以上3 个条件。Kasami 序列集是一种通过偶数阶M 序列构造生成的二元序列集，只含有−1或1两个元素。M序列是一种特性类似白噪声的二元伪随机序列，它的具体特性可参见文献[17–19]。通过N阶M序列构造出的Kasami 序列集，每个序列ksi(n)的长度为L=2N −1，序列集中的序列个数为2N/2。

根据式(3)， 可定义Kasami 序列的自相关函数为

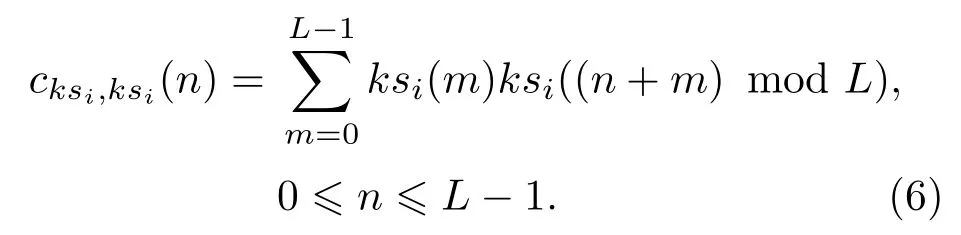
Kasami 序列的自相关函数在n= 0 处取到极大值θ1= 2N −1；设当0 时自相关函数的取值和互相关函数的取值的最大值为θ2，则θ2= 2N/2+1[20]。若N足够大，则θ1≫θ2，可以近似认为满足式(4)的要求。这里解码序列vi(n)=ksi(n)。18 阶Kasami 序列的自相关和互相关特性如图2所示。

N阶(N为偶数)Kasami 序列集的生成方式如下[12]：

(1)首先生成N阶M 序列mls(n)，该序列也是Kasami序列集中的第1个序列；

(2)计算序列长度L= 2N −1 和采样因子d= 2N/2+ 1，定义采样序列e(n)= mls(d × nmodL)；

(3)计算Kasami序列ksτ(n)=mls(n)e((n−τ)modL)，其中，0nL −1。

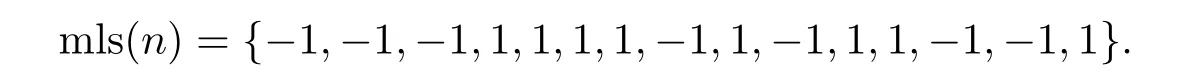
该序列长度L=24−1=15，采样因子d=+1=5。则

这实际上是一个周期内的采样序列{−1,1,1}重复5次：

当τ=3时，e((n −3)mod 15)与e(n)相同，故不重复的e((n −τ)modL)只有3个，这样Kasami序列为

图2 Kasami 序列相关特性Fig.2 Correlation properties of Kasami sequences

1.3 OPS信号的性质和生成方法

根据以上描述可知，以Kasami 信号作为测量信号，虽然满足了测量信号所必须的3 个条件，但是实际上也为测量信号引入了两个新的约束：(1)测量信号和解码信号都是二元信号；(2)测量信号与解码信号相同。这两点对于声学测量而言并不是必要的，但是却限制了编码信号和解码信号的可选空间，使得Kasami 信号的相关特性仍存在较大的可优化空间。如果突破了这两个不必要的约束条件，拓展了编码信号和解码信号的可选空间，则可以找到相关特性更好的序列集。

在这些可能的序列集中，OPS 信号是一种同样满足测量信号所必须的3 个条件、但是相关特性优于Kasami 信号的序列集。OPS 信号是一种通过屏蔽二进序列偶构造的，部分特性类似于Kasami 序列集的伪随机信号。它的编码信号是二元信号，而解码信号是三元信号，编解码信号并不相同。所以OPS 信号不满足Kasami 信号及其类似信号对测量信号的限制条件，拓展了编码信号和解码信号的可选空间，进而获得了更好的相关特性。

设存在序列x(n)={x0,x1,x2,,xM1−1}和y(n)={y0,y1,y2,,yM1−1}。若序列满足以下条件：

其中，xj ∈{−1,1}，则称序列(x(n),y(n))为屏蔽二进序列偶[14]。

根据式(3)，可定义屏蔽二进序列偶的自相关函数cx,y(n)为

若屏蔽二进序列对的周期自相关函数cx,y(n)满足

则称(x(n),y(n))为最佳屏蔽二进序列偶，这里E为大于0的常数。

使用数值搜索的方式寻找最佳屏蔽二进序列偶耗时颇长，文献[21]中提出可采取以下方式构造最佳屏蔽二进序列偶：对于一个长度为奇数的伪随机序列(例如M 序列)，将其中的“−1”都改为“0”，则原伪随机序列和新序列构成最佳屏蔽二进序列偶。

根据文献[13]，OPS 信号的编码矩阵U与解码矩阵V为

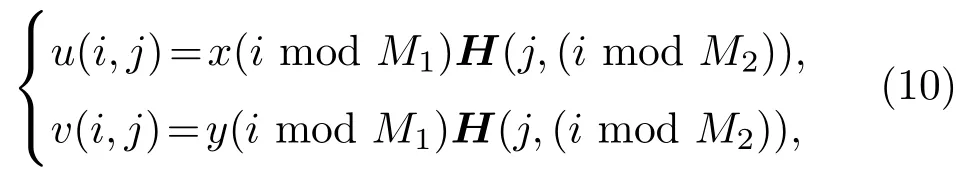
综合文献[13]和文献[21]，OPS 信号生成的具体方法如算法1 所示。以M1= 3 的M 序列和M2=2的Hadamard矩阵为例，OPS信号的构造过程如下：

(1)生成M1=3的M序列{1,−1,−1}；

(2)利用M 序列构造最佳屏蔽二进序列偶：x(n)={1,−1,−1}，y(n)={1,0,0}；

(3)利用最佳屏蔽二进序列偶和Hadamard 矩阵构造编码矩阵U与解码矩阵V。

算法1：OPS 信号的生成算法(1)procedure M1 M2(2)MLS ←mls(M1) △生成长度为M1的M 序列(3) x,y ←MLS(4)for 0 images/BZ_36_1541_1147_1571_1180.pngn images/BZ_36_1612_1147_1641_1180.pngM1 −1(5)if y(n)==−1 then y(n)←0△将序列y中的所有−1均改为0(6)end(7)end(8) H ←hadamard(M2)△生成大小为M2×M2 的Hadamard 矩阵(9)for 0 images/BZ_36_1529_1542_1559_1575.pngi images/BZ_36_1591_1542_1620_1575.pngM1M2 −1(10)for 0 images/BZ_36_1594_1598_1624_1631.pngj images/BZ_36_1659_1598_1689_1631.pngM2 −1(11)u(i,j)←x(i mod M1)H(j,(i mod M2))(12)v(i,j)←y(i mod M1)H(j,(i mod M2))(13)end(14)end

根据式(3)， 可定义OPS 信号的周期相关函数为

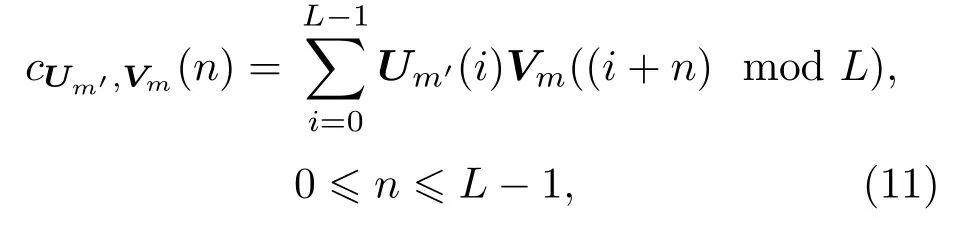
这里Um′和Vm分别表示矩阵U的m′列和矩阵V的m列。当m′=m时，称为自相关函数；当m′m时，称为互相关函数。对于总长度为L= 218、M2= 4 的OPS 信号，其中第1 列信号的自相关函数和第1 列与第2 列信号的互相关函数如图3所示。由于OPS信号的自相关函数呈周期性，实际测量时只需要取0nM1−1的结果即可。

为定量衡量OPS 信号和Kasami 信号的相关特性，定义自相关旁瓣峰值(Autocorrelation sidelobe peak, ASP)和互相关旁瓣峰值(Crosscorrelation sidelobe peak, CSP)如下：若信号的自相关序列为AC(n)(0nL −1)，这里L表示自相关序列长度，则

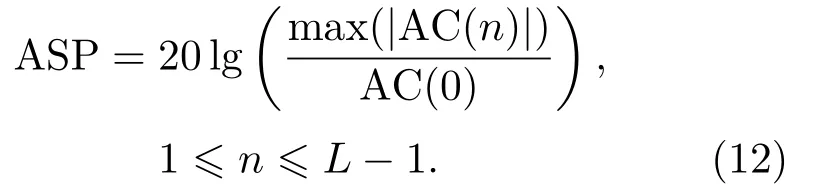
若信号的互相关序列为CCm1,m2(n)(0nL−1,0m1M −1,0m2M −1,m12)，这里M表示序列集中的序列个数，m1、m2表示序列编号，则

旁瓣峰值越小，则说明序列集的相关特性越好。序列个数为4 时，OPS 信号和Kasami 信号的ASP和CSP随序列阶数的变化如图4所示。

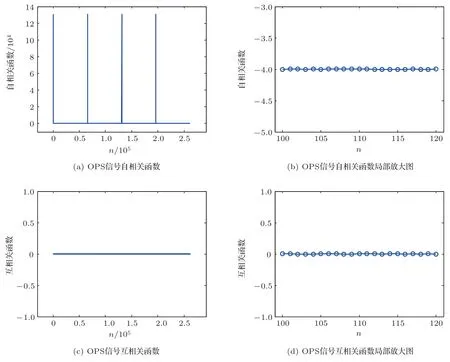
图3 OPS 信号相关特性Fig.3 Correlation properties of OPS

由图4可知，OPS 信号相比Kasami 信号，具有更小的自相关和互相关旁瓣，它的自相关函数更接近理想冲激信号，互相关函数更接近0。所以用OPS信号作为测量信号，各通道间的相互干扰会更小，测量结果的误差也就会更小。

图4 OPS 信号和Kasami 信号的ASP 和CSP 随序列阶数的变化Fig.4 Variation of ASP and CSP with sequence order of OPS signal and Kasami signal

2 仿真验证

为了研究不同测量信号对测量结果的影响，本文采用数值方法对房间脉冲响应进行仿真计算,其具体如下：(1)本文以一组实测扬声器单元的线性参数和非线性参数为参考值，使用前向欧拉法对非线性扬声器的状态空间进行建模[22]，以得到不同测量信号激励下，扬声器的输出信号；(2)利用镜像声源法，得到不同声源对同一个传声器的房间脉冲响应，该方法中最大镜像声源个数由吸声系数决定[23]；(3)用扬声器的输出信号和房间脉冲响应进行卷积，模拟出实际测量中每个声源到达传声器的信号；(4)如果是同时测量信号，则将各个声源的信号叠加，作为传声器的实际接收信号；(5)使用不同测量信号各自计算房间脉冲响应的方法，计算出房间脉冲响应。为对比各方法的仿真结果，本文定义以理想冲激信号为激励信号，线性参数相同、非线性参数为0 的线性扬声器作为声源计算出的房间脉冲响应为房间脉冲响应的参考值。

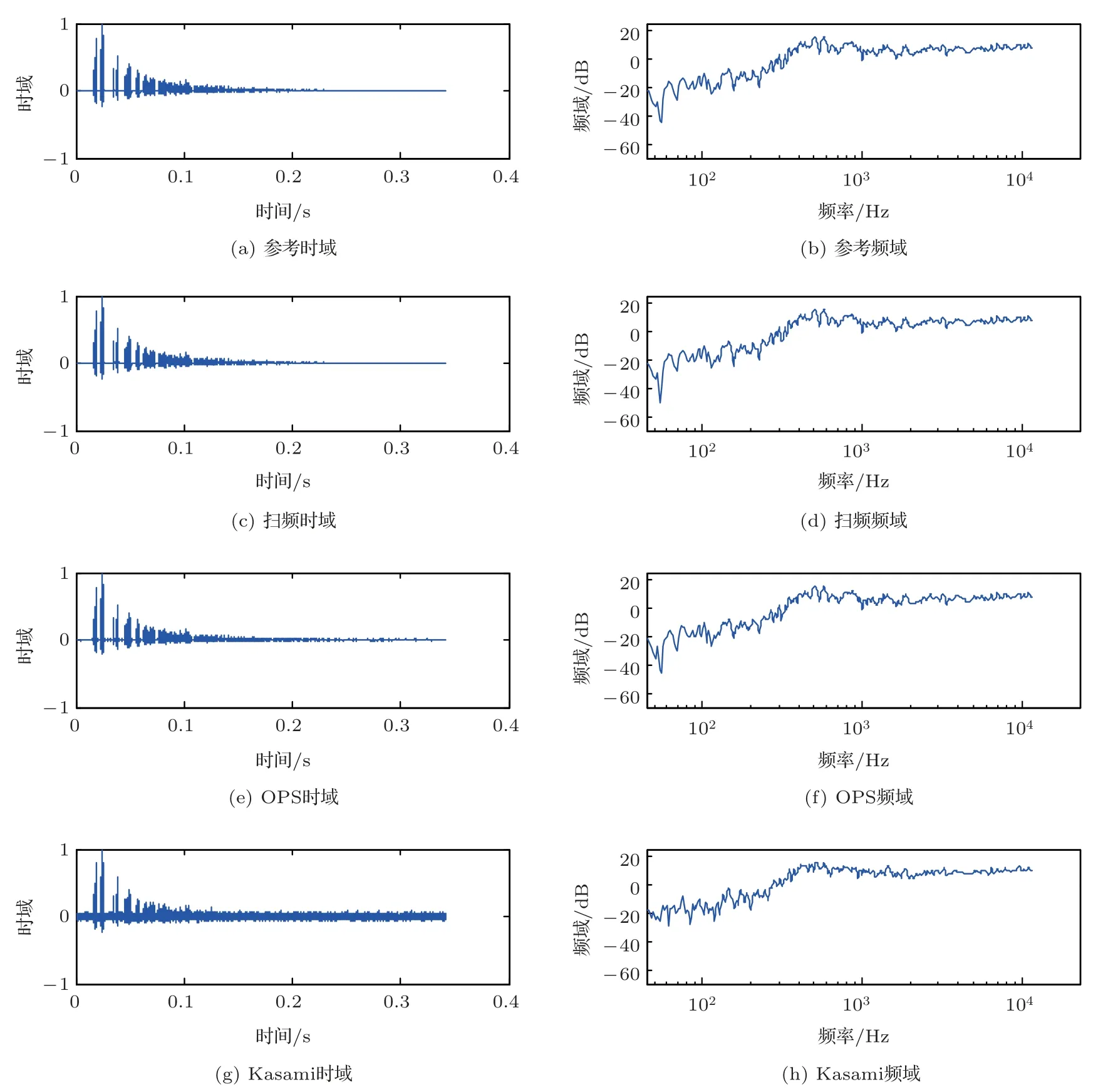
图5 3 种信号测量结果与参考值对比Fig.5 Comparison of measurement results from three kind of measurement signal and actual value

该仿真实验的具体参数如下：信号的采样率fs= 48 kHz，3 种测量信号分别为16 阶Kasami 信号(在48 kHz采样率下约为1 s)、16阶OPS信号、同样长度的对数扫频信号(起止频率分别为2 Hz 和24 kHz)，所有激励信号的峰值均设为1；房间尺寸为6 m×6 m×6 m，吸声系数为0.3；声源数量为4个，声源和传声器的位置随机生成；每个激励信号添加信噪比为50 dB 的高斯白噪声。这里信噪比的计算公式为

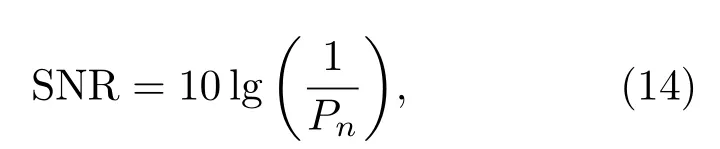
其中，Pn表示白噪声的功率。分别计算3 种激励信号对应的房间脉冲响应和参考房间脉冲响应，并对频域响应做1/36倍频程平滑，其中第一个声源对应的房间脉冲响应如图5所示。

从时域响应可以看出，采用Kasami 信号进行测量，会导致得到的测量结果的底噪较大，进而降低了测量的准确度；采用OPS 信号进行测量，也会导致得到的测量结果含有部分底噪，但是该底噪比Kasami 信号测量结果的底噪小大约30 dB。由于Kasami信号、OPS 信号与扫频信号长度相同，而Kasami 信号、OPS 信号可以多声源同时测量，故而Kasami 信号、OPS 信号的测量速度是扫频信号的4 倍。

为定量比较3 种测量方法在不同频段的频响测量准确度，定义相对误差

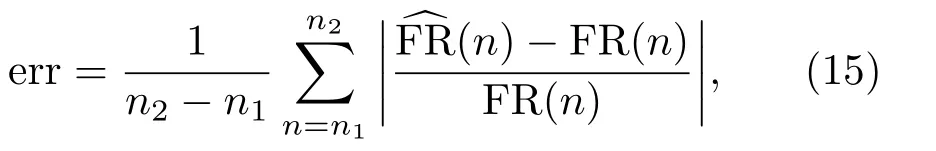
以下设计5 个仿真实验，分别研究声源数量、附加白噪声、序列阶数、吸声系数、非线性特性对不同频段测量误差的影响。为定量研究非线性特性的影响，本文使用非线性增益来表示系统的非线性特性的大小。非线性增益定义为仿真实验中设定的非线性参数与参考非线性参数的比值。设定5 个仿真实验的基本参数为：声源个数为8 个，附加白噪声信噪比为50 dB，序列阶数为18，吸声系数为0.4，非线性增益为1，信号采样率均为48 kHz，扫频信号的起止频率均为2 Hz 和24 kHz。在仿真中，不同信号的长度均近似相等，每个实验重复100 次并将结果进行平均。对于每个仿真实验，除了所研究的参数外，其余仿真参数均为基本参数。为分别研究上述5 个因素对不同频段测量误差的影响，本文设定了2∼24个不等个数的声源进行仿真，其结果如图6所示；设定附加白噪声信噪比区间为45∼55 dB，仿真结果如图7所示；设定序列阶数区间为16∼20，仿真结果如图8所示；设定吸声系数区间为0.4∼1，仿真结果如图9所示；设定非线性增益区间为0∼20，仿真结果如图10所示。

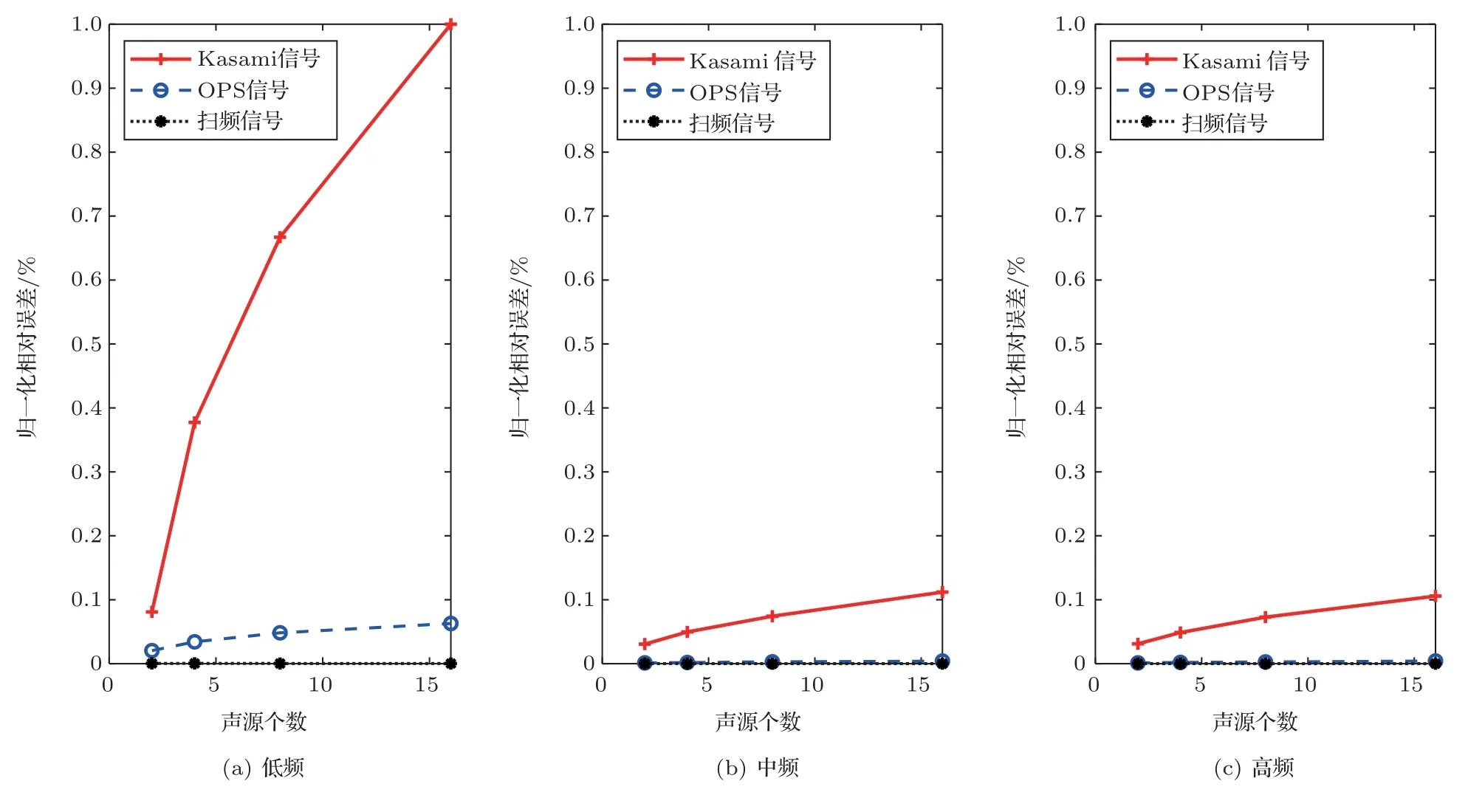
图6 不同声源个数下，各频段测量结果的相对误差Fig.6 Relative error of measurement results in different frequency bands with different number of sound sources

根据图6∼10 可知：扫频信号的测量结果最准确，而且几乎不受所研究的5 个因素的影响；OPS信号的测量准确度在低频低于扫频信号，在中高频几乎与扫频信号相当；Kasami 信号测量结果误差最大；OPS 信号和Kasami 信号的测量误差主要集中于低频，中高频的误差较小，这是因为测量系统的低频能量较低，容易受到其他因素的干扰。由图6可知，同时测量的声源个数越多，各通道间的干扰就越大，测量误差越大；由图7可知，附加白噪声的信噪比的变化，对3 种信号的测量误差几乎没有影响；由图8可知，序列阶数越高，信号越长，OPS 信号和Kasami 信号的测量结果越准确；由图9可知，吸声系数越大，越接近消声室环境，OPS 信号和Kasami信号的误差越小；由图10可知，非线性增益对3 种信号的测量误差几乎没有影响。对比图6∼10 可以发现，对OPS 信号和Kasami 信号的测量误差影响最大的因素是声源个数和序列阶数，其次是吸声系数，这说明OPS 信号和Kasami 信号的测量误差主要是由多通道干扰所产生的噪声引起，也容易受到房间的反射声和混响声的影响。

图7 不同附加噪声信噪比下，各频段测量结果的相对误差Fig.7 Relative error of measurement results in different frequency bands with different SNR of additional noise

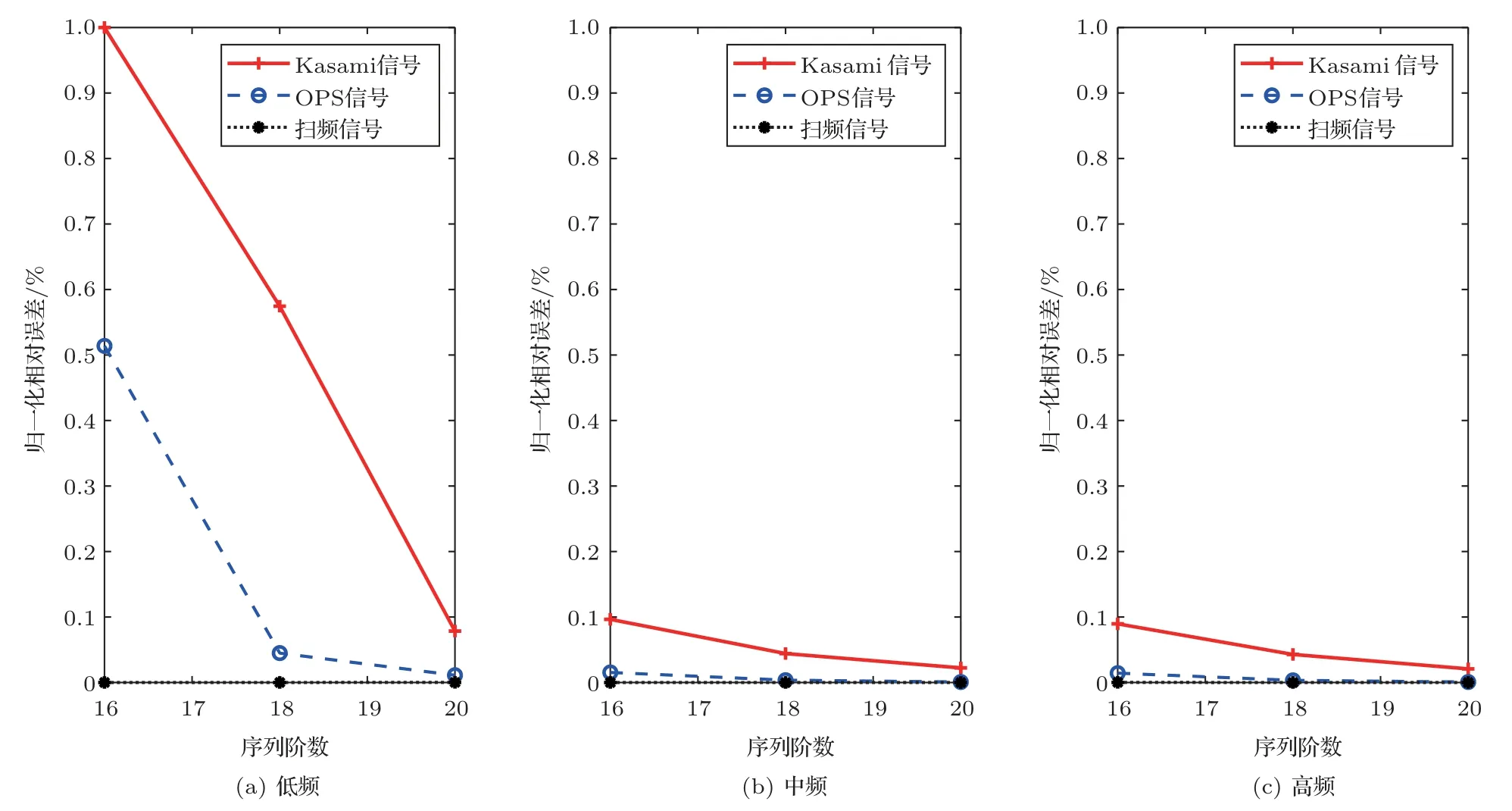
图8 不同序列阶数下，各频段测量结果的相对误差Fig.8 Relative error of measurement results in different frequency bands with different order of sequences

图9 不同吸声系数下，各频段测量结果的相对误差Fig.9 Relative error of measurement results in different frequency bands with different absorption coefficients

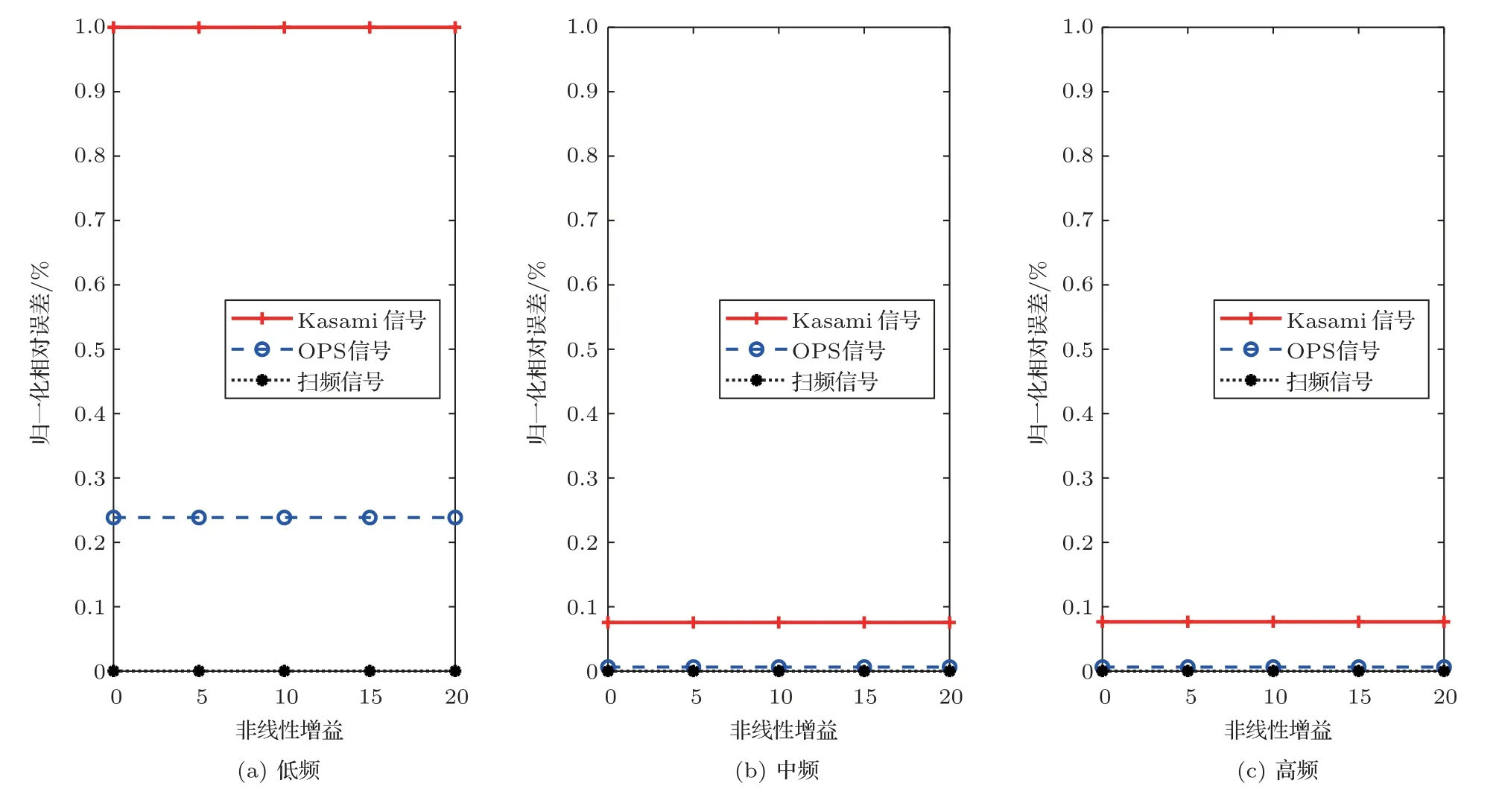
图10 不同非线性增益下，各频段测量结果的相对误差Fig.10 Relative error of measurement results in different frequency bands with different nonlinear gains

3 实验验证

为了验证本文提出的方法，在视听室(房间尺寸约为6 m×7 m×3 m)开展了验证实验，其概况如图11所示。在实验测量链路中，声源激励信号数据由计算机生成，通过声频接口(FIREFACE UC，RME)馈给8 台有源音箱(R1000TC，漫步者)，由一个全指向型扩散场传声器(TYPE 4943，Brüel& Kjær)接收信号，再通过声频接口传递给计算机分析处理，其概况如图12所示。本文分别使用扫频、Kasami 信号、OPS 信号作为测量信号，信号长度约为218点，采样率为48 kHz，持续时间约为5.5 s，扫频信号的起止频率分别为16 Hz 和24 kHz。采用扫频信号时，每个声源依次发声。采用Kasami信号和OPS信号时，为8个声源同时发声，时域测量结果如图13所示。

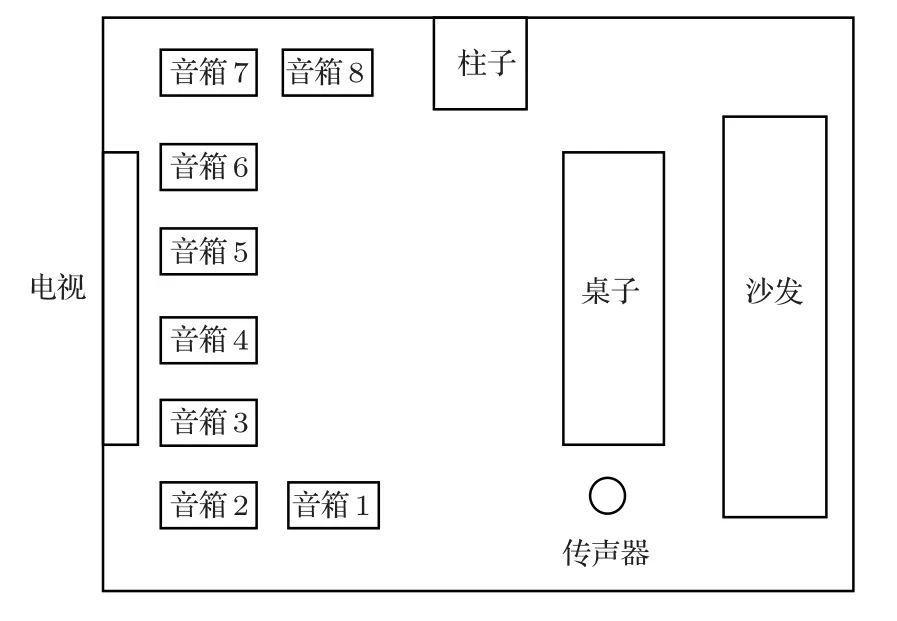
图11 视听室示意图Fig.11 Illustration of audio-visual room

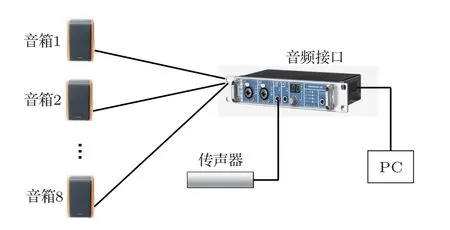
图12 实验设备示意图Fig.12 Illustration of experiment setup

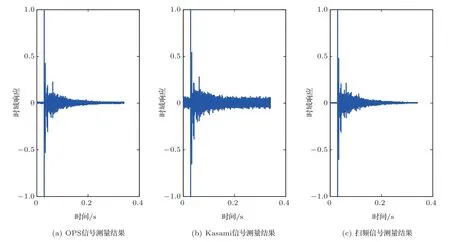
图13 3 种信号的时域测量结果(对应第一个声源)Fig.13 Measurement results of three kind of measurement signal in time domain

本文以扫频信号测得的频响为参考值，分别计算采用Kasami 信号和OPS 信号时的相对误差，并根据最大值做归一化处理，其结果如图14所示。结果表明：(1)整体而言，相比Kasami信号，采用OPS信号可以显著降低测量结果的噪声，从而降低测量误差；(2)在低频部分，无论采用Kasami 信号还是OPS信号，测量结果和参考值相比都有较大的偏差，而在中高频部分采用OPS信号则误差较小。

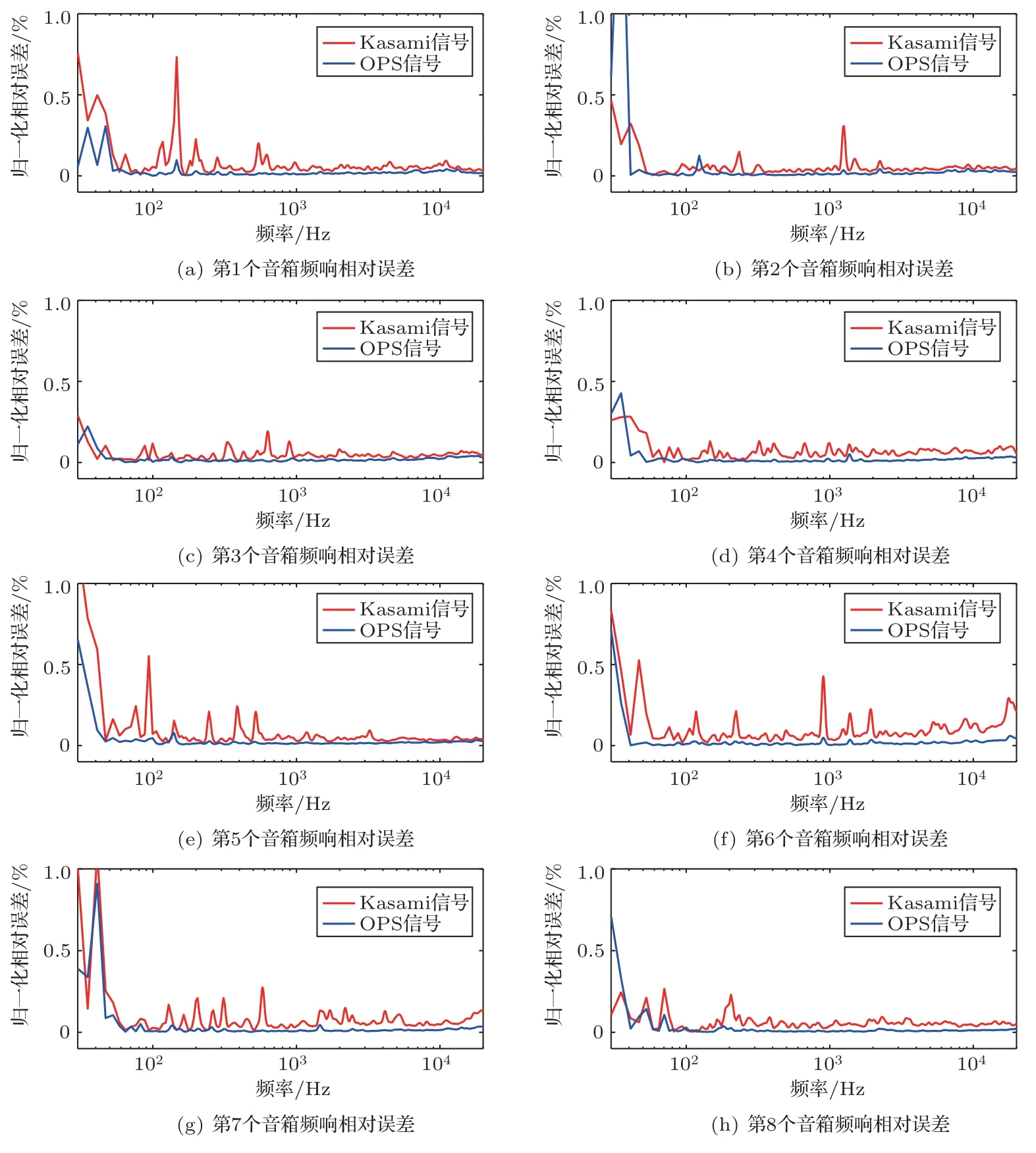
图14 8 个声源Kasami 信号和OPS 信号测量结果的相对误差Fig.14 Relative errors of measurement results from Kasami signal and OPS signal in 8 sources

为比较采用两种激励信号在不同频段误差的大小，本文根据式(15)分别计算得到低频部分(小于250 Hz)、中频部分(250 4000 Hz)、高频部分(大于4000 Hz)Kasami 信号和OPS 信号测量结果对应的相对误差，式(15)中的n1、n2分别为对应频段分界频率对应的频率采样点，8 个声源的测量误差如图15所示。结果表明：Kasami 信号和OPS 信号对应的测量误差在中频和高频较低，在低频较大；相比Kasami信号，采用OPS信号的测量误差较小。

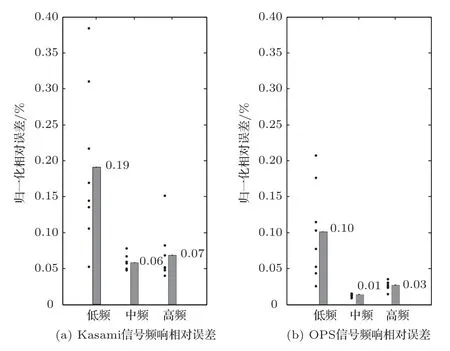
图15 采用Kasami 信号和OPS 信号的测量结果在不同频段上的相对误差Fig.15 Relative errors of measurement results from Kasami signal and OPS signal in different frequency band

4 结论

本文提出了一种基于三元伪随机序列集的多声源同时测量方法，利用其良好的相关特性，可以实现多个声源的同时测量。相较于Kasami信号，本文提出的激励信号具有更好的相关特性，更低的旁瓣峰值。仿真结果表明，相较于Kasami 信号，采用本文提出的激励信号的测量误差较小。为了验证本文提出的测量方法的准确性，在视听室中开展测量实验。实验结果表明，采用本文提出的方法测量房间响应，具有较低的测量误差。在需要对多个声源进行测量的应用场景中，采用这一方法可以提高测量效率，降低由于各通道不同步导致的误差。