挖掘机驾驶室低频结构噪声分析与优化∗

2021-04-28刘志恩王亚磊柴鹏飞李晓龙刘跃吉

应用声学 2021年2期

关键词：驾驶室传递函数挖掘机

刘志恩王亚磊柴鹏飞李晓龙刘跃吉单昆吴锦

(1 现代汽车零部件技术湖北省重点实验室武汉 430070)

(2 汽车零部件技术湖北省协同创新中心武汉 430070)

(3 徐州工程机械集团有限公司徐州 221005)

0 引言

随着挖掘机行业的快速发展，人们不仅仅满足于挖掘机的工作性能，对其舒适性能提出了更高的要求，尤其是挖掘机的噪声、振动、舒适性(Noise,Vibration, Harshness, NVH)特性。在挖掘机NVH特性研究中，驾驶室的振动和驾驶员耳旁的噪声有直接的关系，减小驾驶室的振动噪声，可以提高驾驶员的舒适性和工作效率，故对挖掘机驾驶室的噪声研究和分析具有重要的意义[1]。

驾驶室的噪声分为结构声和空气声，而研究表明，当驾驶室密封效果较好时，内部噪声主要以结构声为主[2]。结构声主要是由于发动机的激励通过回转平台传递到驾驶室，引起驾驶室壁板振动并向车内辐射噪声，这类噪声主要是20∼200 Hz 的低频噪声[3]。

本文基于某小型液压挖掘机驾驶室，通过噪声传递函数(Noise transfer function, NTF)分析对驾驶室低频噪声进行研究。首先建立驾驶室有限元模型，计算各工况下驾驶室噪声传递函数分析，运用统计学方法确定主要噪声峰值频率及相应工况；通过模态声学贡献度计算，确定危险工况下噪声贡献量较大的模态阶数，参照模态振型确定驾驶室振动变形最大的车身板件；并对该板件进行形貌优化处理，提高其一阶固有频率，有效降低了驾驶室的噪声传递函数在危险频率下的峰值。

1 驾驶室有限元模型的建立

有限元模型的准确建立是仿真分析的基础。首先建立驾驶室白车身(Body in white, BIW)的有限元模型。将驾驶室的三维数模导入Hypermesh 软件，对几何模型进行清理。驾驶室白车身多为板件结构，采用尺寸为8 mm 的四边形壳单元划分，然后建立相应的连接，驾驶室围板之间多为点焊和缝焊，分别采用ACM 单元和RBE2 单元模拟，得到白车身有限元模型如图1所示。

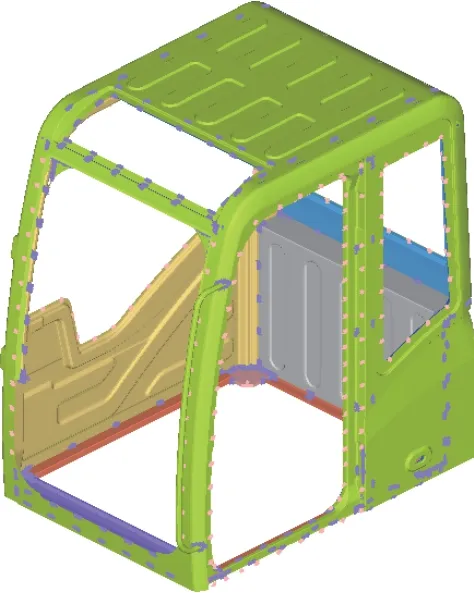
图1 白车身有限元模型Fig.1 Finite element modal of BIW

在白车身模型的基础上，添加车门、门窗玻璃和地板等结构，车门和驾驶室之间通过RBE2 连接来模拟门锁，玻璃和板件之间采用胶粘连接，最后，得到驾驶室结构有限元模型如图2所示，其中壳单元共282634 个，三角形单元3888 个，实体单元50796个。

图2 驾驶室结构有限元模型Fig.2 Finite element modal of cab structure

2 噪声传递函数分析

2.1 噪声传递函数模型建立

噪声传递函数也称为灵敏度，指在结构上输入的单位激励和噪声响应之间的关系，可以真实地反应系统的固有特性，使声压频率更加清晰[4]。挖掘机驾驶室的NTF分析基于结构与声腔组成的声-固耦合有限元模型，在悬置上施加单位激励得到驾驶员耳旁的声压级响应，进而识别出噪声的峰值频率。

进一步划分驾驶室声腔网格。提取驾驶室内表面，补上大的孔和缝隙，使其形成封闭的空腔，然后进行声腔网格的划分。声学单元的理想尺寸L是每个波长至少6个单元，故L应满足[5]：

式(1)中：v是声速，f是求解的最大频率。

该挖掘机所关注的是20∼200 Hz 的低频噪声，故声腔网格尺寸L283 mm，考虑到计算精度的影响，取L为50 mm，得到的声腔网格模型如图3所示。在Optistruct 有限元分析软件中通过添加“ACMODL,DIFF”卡片将驾驶室结构模型和声腔模型进行耦合[6]，得到驾驶室声-固耦合模型，如图4所示。

图3 声腔模型Fig.3 Acoustic cavity model

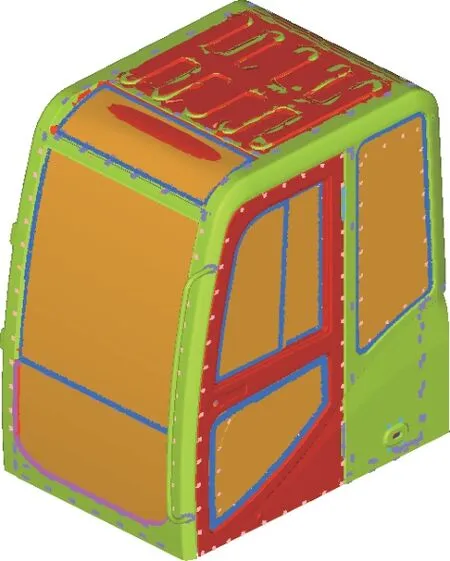
图4 声-固耦合模型Fig.4 Acoustic-solid coupling model

2.2 噪声传递函数计算

本文所研究的挖掘机，其发动机的激励力经回转平台通过4 个悬置传递至驾驶室地板，故对驾驶室进行NTF 分析时，在驾驶室4 个悬置安装点上分别施加x、y、z三个方向的单位激励力，共计12个工况，在驾驶室声腔内以驾驶员耳旁为声压级响应点。为了提高计算速度，本文采用了模态叠加法进行计算，模态计算频率在0∼400 Hz，输出求解范围为20∼200 Hz，最终计算得到12个工况的NTF曲线。图5所示分别为4 个悬置安装点x、y、z三个方向激励的NTF曲线。

图5 驾驶室4 个悬置安装点激励下的NTF 曲线Fig.5 The NTF curve stimulated by four suspended installation points of the cab

2.3 结果分析

汽车行业规定车身声学灵敏度目标值为55 dB，考虑到挖掘机驾驶室和汽车驾驶室的结构差异以及工程机械NVH 性能要求没有汽车严格，设定挖掘机驾驶室声学灵敏度目标值为60 dB。对所得到的NTF 曲线进行分析，将峰值大于60 dB所对应的频率定义为危险频率，通过对12个工况的危险频率进行统计，频率35 Hz 出现的次数最多，所以将35 Hz 确定为需优化的频率。其中频率35 Hz 所对应的7 个危险工况分别为左前悬置安装点、左后悬置安装点、右后悬置安装点的y、z向激励和右后悬置安装点的z向激励。

3 模态声学贡献度计算

3.1 模态声学贡献度基本理论

模态是结构系统的固有振动特性，机械结构中任何一点的响应都可以表示为各阶模态的线性组合，即m点的响应可以表示为

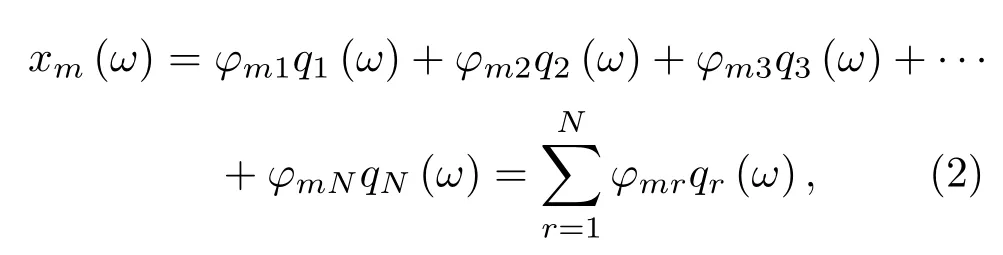
式(2)中，φmr是响应点m的第r阶模态振型系数；qr是第r阶的模态坐标。

模态声学贡献度的计算即是求某阶模态所引起的响应在对总响应中的比重，也就是求模态坐标。通过方程变换可以求得模态坐标为[7]

式(3)中，fmr、Kr、Mr、Cr别表示第r阶激励力、刚度矩阵、质量矩阵、阻尼矩阵。

3.2 计算结果与分析

通过有限元软件进行模态声学贡献度分析，找出35 Hz 下各个工况噪声峰值的主要模态贡献阶数，进而根据驾驶室结构模态振型对振动位移较大的局部结构进行优化，达到降低噪声峰值的目的。

在驾驶室声-固耦合模型中分别加载7 个危险工况对应的激励，计算出驾驶室结构在35 Hz 下的模态贡献量。综合统计这7个工况的模态贡献量，确定对35 Hz 噪声峰值贡献量最大的模态阶数都为第11阶模态，然后根据驾驶室结构第11阶模态的振型图，确定振动位移较大的结构，进行优化。由于篇幅所限，这里仅列出前两个工况的模态贡献量柱状图，如图6所示。

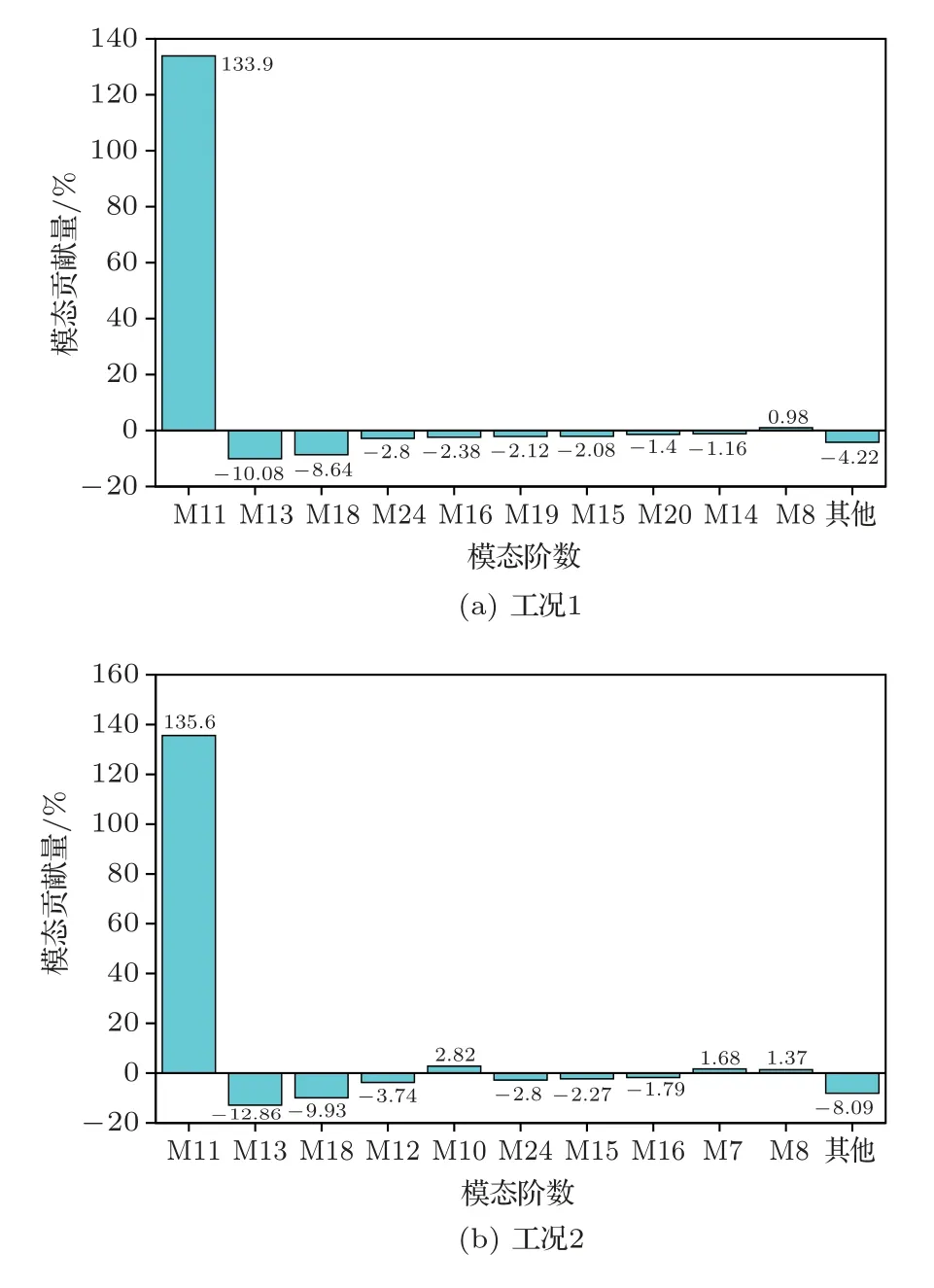
图6 驾驶室模态声学贡献度Fig.6 Contribution of modal acoustics in the cab

图7为驾驶室第11 阶结构模态振型图，可以看出：驾驶室右侧围板的振动位移最大，因此需要对该处结构进行优化，提高其刚度，进而降低驾驶员耳旁的声压级。

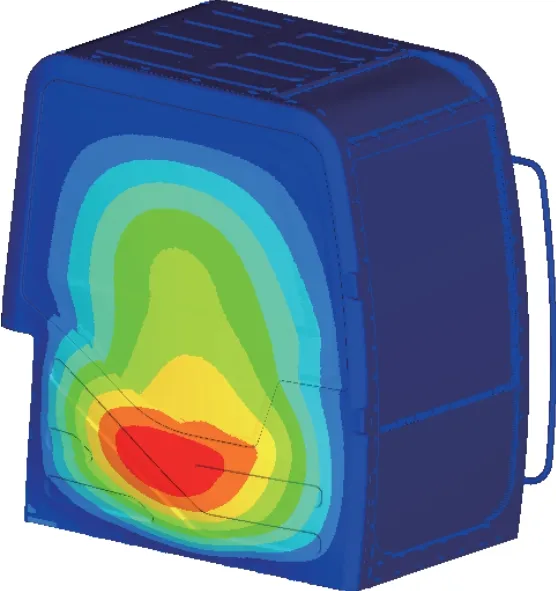
图7 驾驶室第11 阶模态振型云图Fig.7 The 11th-order modal shape cloud image of the cab

4 面板形貌优化

4.1 形貌优化基本理论

结构优化的数学模型可表示为[8]

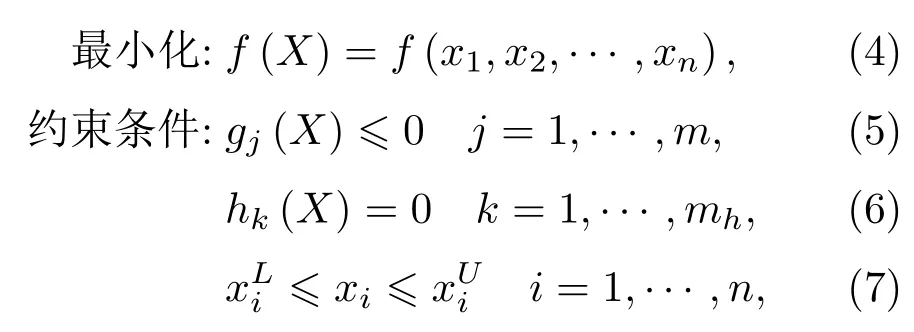
其中，X=x1,x2,···,xn是设计变量；f(X)是目标函数；g(X)是不等式约束函数；h(X)是等式约束函数。

结构优化包含了拓扑优化、形貌优化、尺寸优化、形状优化等，其中形貌优化是一种在板形结构中寻找最优的加强肋分布的概念设计方法，用于设计薄壁结构的强化压痕，在减轻结构重量的同时能满足强度、频率等要求[9]。根据第3 节驾驶室模态贡献量的分析，确定了问题结构是右围板，右围板是薄壁结构，故采用形貌优化，在其结构中找寻最优的加强肋分布设计，提高其刚度。

4.2 右侧围形貌优化

将右围板从驾驶室中单独提取出来，并将原有的加强筋删除，重新建立右围板的有限元模型，将其作为设计区域，其中边界条件为约束右围板四周x、y、z三个方向的平动自由度，释放旋转自由度，然后对其进行形貌优化[10]。

形貌优化问题描述如下：(1)优化目标：右围板一阶模态频率最大化，提高右围板的刚度；(2)设计约束：筋的尺寸，其中筋的尺寸与原结构相同，起筋宽度为65 mm，高度为10 mm，角度为60◦；(3)设计变量：右围板模型节点相对壳单元中性面法向的扰动。在Optistruct 中进行优化计算，右围板优化结构如图8(a)所示。但是该优化结构筋的位置和形状毫无规律，很难制造，故在形貌优化的时，对筋采用上下和左右对称约束，重新进行优化计算，结果如图8(b)所示。

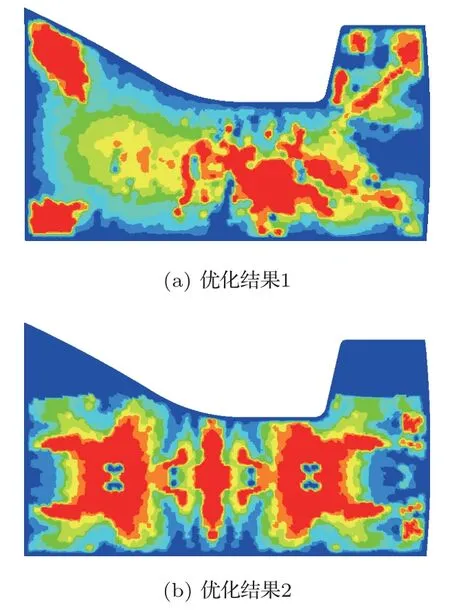
图8 右围板形貌优化结果Fig.8 Right panel shape optimization result

基于形貌优化结果，并结合制造工艺性，设计了右围板的最终结构如图9所示。

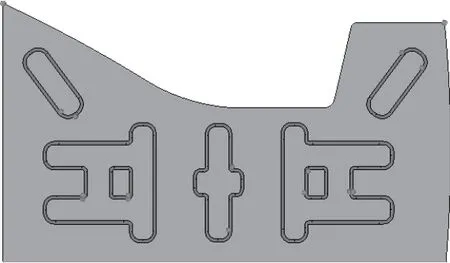
图9 右围板设计的最终结果Fig.9 The final structure of the right panel design

4.3 优化结果仿真预测

由于该挖掘机驾驶室的原结构已经开始量产，对于新结构未加工制造，将通过仿真来预测优化结果。将结构改进后的驾驶室重新进行噪声传递函数计算，得到7 个危险工况的传递函数，与原结果进行对比，由于篇幅所限，这里仅列出前两个工况的对比结果，如图10所示。从图10可以看出，通过对右围板进行结构优化，各工况在35 Hz 处声压级峰值均有所降低，且下降了2∼4 dB，可见驾驶室在结构优化上取得了明显成果。