带忆阻负载的电流型Cuk 变换器动力学分析及其混沌控制

(湘潭大学电子与信息学院,湖南湘潭 411105)

忆阻器作为一种具有记忆效应的新型基本电路元件,自从蔡少棠[1]提出以来就引起了学者的广泛关注。尤其在2008 年惠普实验室首次报道了忆阻器的可实现性后[2],极大地唤起了科研人员对忆阻器开展全方位研究的兴趣。由于忆阻器自身的非线性特性使其更加容易产生混沌电路,从而在保密通信、信息加密等领域也有广泛的应用[3-8]。近些年来,基于忆阻混沌电路的设计与分析已成为相关领域的研究热点。

开关DC-DC 变换器作为开关电源的核心组成部分存在着丰富的非线性动力学现象,例如,Hopf 分岔[9]、边界碰撞分岔[10]、双稳定共存现象[11]等,已在许多文献中被广泛报道。其中负载类型是影响DC-DC变换器的非线性动力学行为的一个重要因素。文献[12]以常规电阻作为负载,研究了电流型Cuk 变换器的分岔与混沌现象以及变换器稳定运行的参数域表达式。文献[13]和[14]在具有恒流负载的变换器中发现了鞍节点分岔和快慢尺度不稳定性等现象。Zhang等[15]开创性地将忆阻器作为单级升压变换器的负载通过数值仿真和电路仿真研究其动力学行为,并通过直流分析阐述了该升压变换器的输出电压主要由忆阻器的内部参数决定,但其只关注了开关周期对该忆阻变换器的稳定性和动力学行为的影响,而忽略了其他参数的影响。随后,文献[16]研究了忆阻负载对峰值电流型Buck-Boost 变换器的动力学影响,发现忆阻负载会扩大该变换器的正常工作区域,但其并未通过解析表达式说明忆阻器参数是如何影响变换器的稳定运行区间的。基于以上研究,为了进一步了解忆阻型DCDC 变换器中各种非线性现象的形成机理,本文推导了系统倍周期临界分岔点的解析表达式,并引入斜坡补偿对忆阻Cuk 变换器进行镇定控制,从而为忆阻器在功率开关元件中的应用提供了一定的理论依据。

本文在传统的Cuk 变换器基础上通过引入一个忆阻器从而构建了一个新的五维非线性时变系统。首先,通过数学建模、数值分析研究了该系统的基本动力学特性。然后,基于能量守恒原理,推导了该变换器关于各参数的稳定运行的解析表达式,得到了关于3 个主要参数的稳定域图,从而进一步揭示了忆阻器参数对该系统的稳定运行的影响。最后,通过在变换器的反馈控制电路中引入恰当的斜坡补偿信号拓宽系统的稳定工作范围,使工作在混沌态的忆阻Cuk 变换器电路进入多周期态、周期2 和单周期态,从而实现该忆阻变换器电路的稳定性控制。PSIM 电路仿真结果证明了理论分析和数值分析的正确性。

1 峰值电流控制型忆阻Cuk 变换器

忆阻器的定义由蔡少棠等[17]概括,其中包括压控忆阻器和流控忆阻器。近十年来,运用模拟元器件来实现的各种忆阻器仿真器[18-20]被广泛报道,并且在基于忆阻器的电路中发现了许多有趣且复杂的动力学行为。由于压控忆阻器更适合基于并联忆阻器的应用电路,因此本文在经典的Cuk 变换器基础上构造一个压控忆阻器仿真器代替Cuk 变换器中的电阻负载,如图1(a)所示。压控忆阻器的数学模型为:

式中:iM和vM分别表示忆阻器两端的电流和电压;W(v0)为忆导;v0为忆阻器内部状态变量;g表示忆阻器等效电路中乘法器的增益。

图1 峰值电流控制型忆阻Cuk 变换器原理图Fig.1 Schematic of the peak current mode memristive Cuk converter

通过用忆阻负载W(v0)代替阻性负载RL,峰值电流模式Cuk 变换器的示意图如图1(b)所示,它由输入电压E、一个开关管S、一个二极管D、两个电感L1和L2、两个电容C1和C2以及忆阻负载W(v0)组成五阶动态电路,电路参数如表1 所示。假设该变换器工作在电流连续模式(Continuous Conduction Mode,CCM)下,则该变换器在一个开关周期内存在两种不同的开关状态,其对应的两种主电路拓扑如图2 所示。

表1 峰值电流模式忆阻Cuk 变换器的电路参数Tab.1 Circuit parameters of peak current mode memristive Cuk converter

图2 不同开关状态对应的电路拓扑Fig.2 Circuit topology corresponding to different switch states

开关状态一:开关管S 导通,二极管D 关断,电感电流iL1线性上升,原电路中的电流路径如图2(a)中虚线所示。根据基尔霍夫电压电流定律,可以得到该开关状态下的系统状态方程:

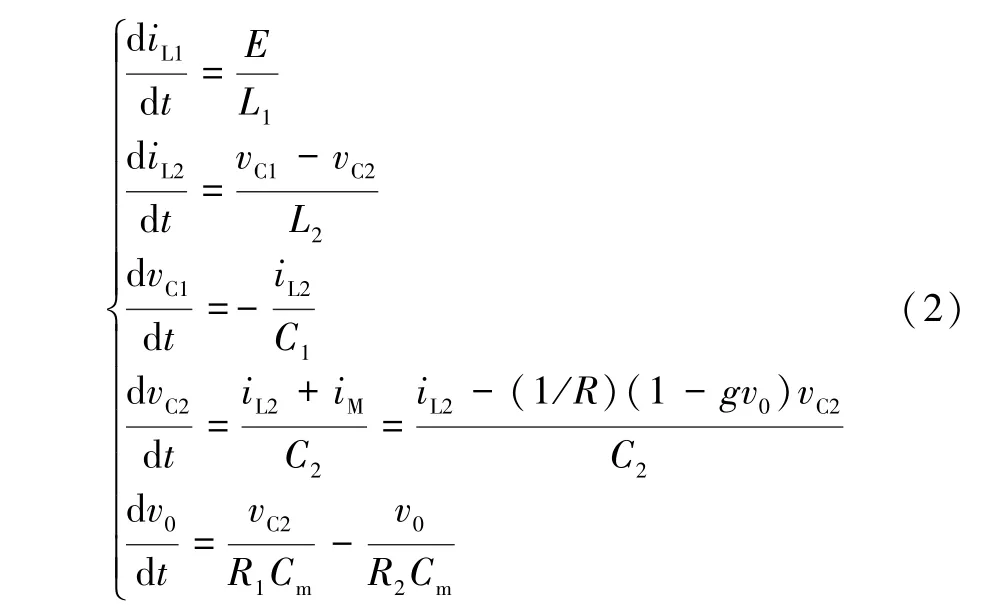
开关状态二:开关管S 关断,二极管D 导通,原电路中的电流路径如图2(b)中虚线所示。相应的状态方程为:

为了便于在Matlab 中进行数值分析,引入x,y,z,u,w这5 个新的无量纲状态变量,令:

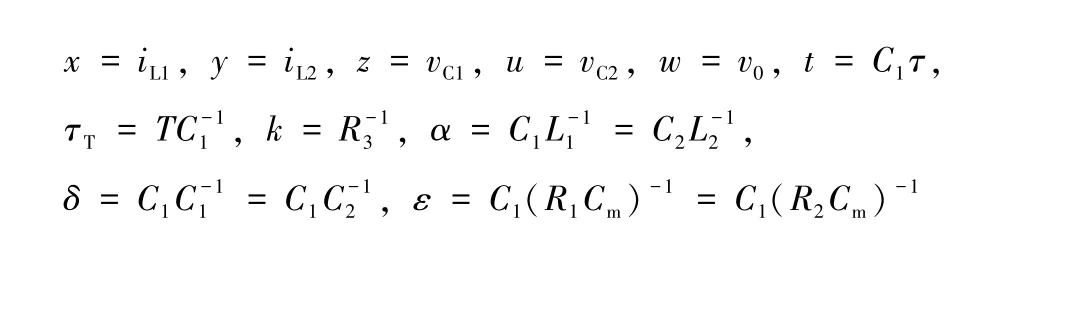
则式(2)和式(3)可以改写为:

式中:Dc表示变换器的导通占空比,变化范围0～1,其中系统的无量纲参数可以通过计算得到τT=0.5,k=0.1,α=0.1,δ=1,ε=5,Iref=4,E=10,g=-0.1。

2 系统动力学分析

2.1 时域波形图

选取参考电流Iref=4 A,其他电路参数如表1 所示,初始值设定为[0,0,0,0,0],可以得到系统状态变量x,u和w的仿真波形如图3 所示,分别代表电感电流iL1、输出电压vC2和忆阻器内部状态变量v0的波形。可知,电感电流iL1在3.4～4 A 之间波动,这时变换器工作在CCM。同时,由于R2Cm电路的相位延迟作用,我们可以清楚地观察到v0的波形滞后于输出电压vC2,变换器工作在混沌状态。其他电路参数固定不变,改变Iref为1 A 时,其相应的时域波形图如图4 所示。此时,电感电流iL1在0.8～1 A 之间波动,变换器同样工作在CCM 模式,且电感电流和输出电压的纹波较小,系统工作在稳定的周期1 状态。

2.2 占空比分析

占空比是描述DC-DC 变换器的一个本质量,更能反应系统非线性动力学的本质特性[14]。通常当负载W(v0)两端的电压是混沌信号和周期信号时,其对应的开关占空比分别是混沌信号和周期信号。当Iref分别为4 A 和1 A 时,变换器在每个开关周期的占空比曲线图分别如图5(a)、5(b)所示。图中无序和规则的占空比Dc进一步说明了当Iref=4 A 和1 A 时,电路系统的工作状态是混沌的和周期的。当Iref分别为4 A 和1 A 时,占空比Dc分别为0.5612 和0.4191。通过计算,可以得到变换器的输出电压分别为12.7893 V 和7.2147 V,与图4 中状态变量u的幅值一致。由此可见参考电流Iref的选取对变换器的稳定性有显著的影响。

图3 峰值电流模式忆阻Cuk 变换器在Iref=4 A 的3 个状态变量时序图Fig.3 Three time sequences of peak current mode memristive Cuk converter when Iref=4 A

图4 峰值电流模式忆阻Cuk 变换器在Iref=1 A 的3 个状态变量时序图Fig.4 Three time sequences of peak current mode memristive Cuk converter when Iref=1 A

图5 占空比Dc曲线图Fig.5 Curves of duty cycle Dc

2.3 倍周期分岔与边界碰撞分岔

一般而言,可引起忆阻Cuk 变换器工作状态发生变化的主要参数有输入电压E、参考电流Iref和忆阻参数g,本节主要以参考电流Iref和忆阻参数g作为分岔参数,研究峰值电流模式下的忆阻Cuk 变换器电路参数在宽范围变化时的动力学行为。

在峰值电流控制型DC-DC 变换器中,一般认为Dc＞0.5 是变换器失去稳定性的一个条件[21]。由式(4)可知电感电流iL1的纹波可以表示为,根据能量守恒定律,可以得到以下方程式:

此外,工作于CCM 模式的峰值电流型忆阻Cuk变换器存在一个电感电流边界Ib可表示为:

随后,将参考电流Iref作为分岔参数并从0.5 A 增加到5 A,峰值电流型忆阻Cuk 变换器的状态变量x的分岔图如图6(a)所示,图中黑色点划线表示电感电流边界Ib。当Iref从0.5 A 逐渐增大到5 A 时,变换器从稳定的周期1 状态在Iref=2.1 A 附近经倍周期分岔进入周期2 的次谐波振荡;当Iref=2.3 A 时,Cuk 变换器电感电流iL1的运行轨道与电感电流Ib相遇发生边界碰撞分岔进入混沌状态。将表1 中的电路参数代入到式(7)可计算出系统的倍周期分岔点为Iref,pbd=2.125 A,与图6(a)结果一致。当参考电流分别选为Iref=0.5 A、Iref=2.1 A、Iref=3 A 和Iref=5 A 时,峰值电流型忆阻Cuk 变换器在x-w平面的相轨图如图7 所示。图中所示的相轨图所反映的Cuk 变换器的工作状态与图6(a)所示的分岔图所描述的运行状态是完全一致的。简而言之,随着Iref的增加,忆阻Cuk 变换器具有从周期1 极限环到周期2 极限环,到成对的混沌吸引子,最后到复杂的混沌吸引子的动态过渡。

图6 以Iref为分岔参数在不同负载类型下的分岔图Fig.6 Bifurcation diagram using Irefas bifurcation parameter with different types of load

当g=0 时,代入式(3)表明忆阻器W(v0)相当于一个阻值为R3的电阻,此时以参考电流Iref为分岔参数得到的分岔图如图6(b)所示。与图6(a)对比,图中的倍周期分岔点发生在Iref=1.1 A 左右,变换器的稳定周期1 区间变得更窄。参考式(7),将g=0 代入得参考电流的倍周期分岔点为Iref,pbd=1.125 A,与图6(b)现象一致。同时,从式(7)可得影响变换器的稳定性参数主要有电源电压E,参考电流Iref、忆阻器内部参数g、开关频率f等。以参数g为可变参数,记录每个开关周期的占空比Dc可画出如图8(a)所示的峰值电流型忆阻Cuk 变换器随忆阻器内部参数g在(-0.6,0)变化的分岔图。可见随着g的绝对值的增大,系统从混沌态进入周期1 态,占空比Dc也慢慢减小到0.5以下。换而言之,当用忆阻负载替换传统电阻负载作为Cuk 变换器的负载时,系统具有更大的稳定工作区间。将Dc≤0.5 代入到式(6)可得变换器关于参数Iref、E和g稳定运行的参数域为:

图7 对于参考电流Iref的不同值,变换器在x-w 平面上的相图Fig.7 For different values of the reference current Iref,phase portraits of the converter in the x-w plane

图8 分岔图和峰值电流模式忆阻Cuk 变换器的稳定参数区域Fig.8 Bifurcation diagram and the stable parameter region of the peak current mode memristive Cuk converter

图8(b)给出了参数在g=-0.6～0 和E=2～22 V变化时,相应的Iref分岔点所形成的曲面,曲面上方对应于变换器的不稳定运行参数域,式(9)的预测结果与分岔图所反映的数值模拟结果吻合较好。

2.4 引入斜坡补偿信号后的混沌控制

斜坡补偿控制是一种直观有效的稳定性控制技术,通过引入适当的斜坡补偿电流或电压能有效地拓宽变换器的稳定范围[22-24]。如图9 所示,将斜坡补偿信号加入到Cuk 变换器的反馈控制电路从而得到了工作于CCM 的忆阻Cuk 变换器的电感电流iL1的波形示例。图中,Iref为参考电流,iref为补偿后的参考电流,mc为斜坡信号的斜率,可得补偿后的参考电流iref与原参考电流Iref的关系为:

式中:T为开关周期;(tmodT)表示t对T取模运算,且斜坡补偿信号的频率与变换器的开关频率相等。

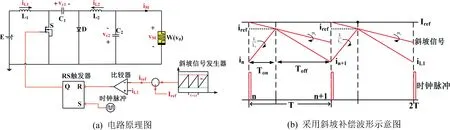
图9 斜坡补偿电流控制忆阻Cuk 变换器原理图及其电感电流波形示例Fig.9 The schematic diagram of the slope compensation current control memristive Cuk converter and its inductor current waveform example

首先,分别引入斜坡补偿斜率mc=0(无斜坡补偿信号)、mc=0.05、mc=0.15 和mc=0.25,此时以输入电压E为分岔参数,忆阻Cuk 变换器的分岔图如图10 所示。从图中可以看出当无斜坡补偿信号引入时,变换器的周期1 区间为16.2～20;在mc=0.05 时,系统的周期1 区间为14.5～20;当mc=0.15 时,系统的周期1 区间为10.6～20;当mc=0.25 时,变换器在E为5～20 V 之间都工作在稳定的周期1 状态。由此可得采用的斜坡补偿信号斜率mc越大,忆阻Cuk 变换器的稳定区间就越宽,表明斜坡补偿可以有效地拓宽系统的稳定范围。

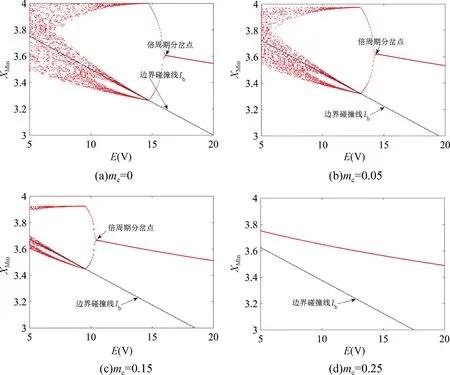
图10 峰值电流模式忆阻Cuk 变换器引入不同斜坡补偿斜率的分岔图Fig.10 Bifurcation diagram for the peak current mode memristive Cuk converter with compensating ramp signal

图11 给出了忆阻Cuk 变换器的电感电流iL1的时域仿真波形。在100 ≤τ ＜150 时,无斜坡补偿信号引入,变换器电路工作在混沌态。在τ=150 时,分别引入mc=0.05、mc=0.15 和mc=0.25 的斜坡补偿信号,变换器电路分别进入了多周期状态、周期2 状态和稳定的周期1 状态。由此说明,对处于混沌状态的忆阻Cuk 变换器,只要引入一个适当斜率的斜坡补偿信号,就能使Cuk 变换器的工作状态镇定在稳定的周期1 状态。

3 电路仿真验证

为进一步验证先前的理论分析,基于PSIM 构建了具有忆阻负载的Cuk 变换器电路,如图12 所示。设置时钟脉冲宽度为0.25 μs,比较器的输入端参考电流Iref实际上是一个电压信号(即Iref=4 V)。选取表1 中的电路参数并设置五个状态变量的初始值为(0,0,0,0,0)。

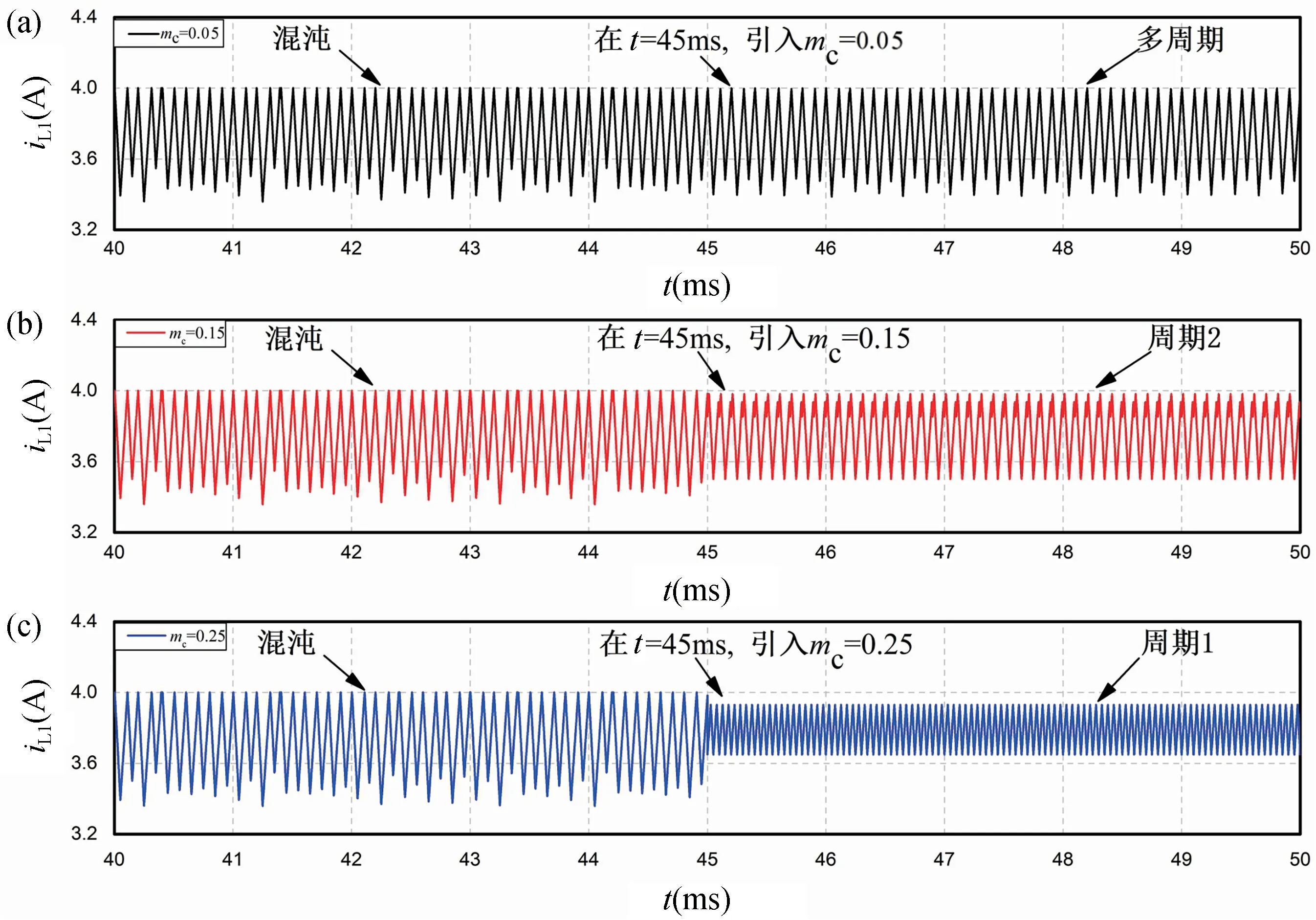
图11 引入不同mc后的电感电流iL1的镇定控制Fig.11 Stabilization control of inductor current iL1after introducing different mc

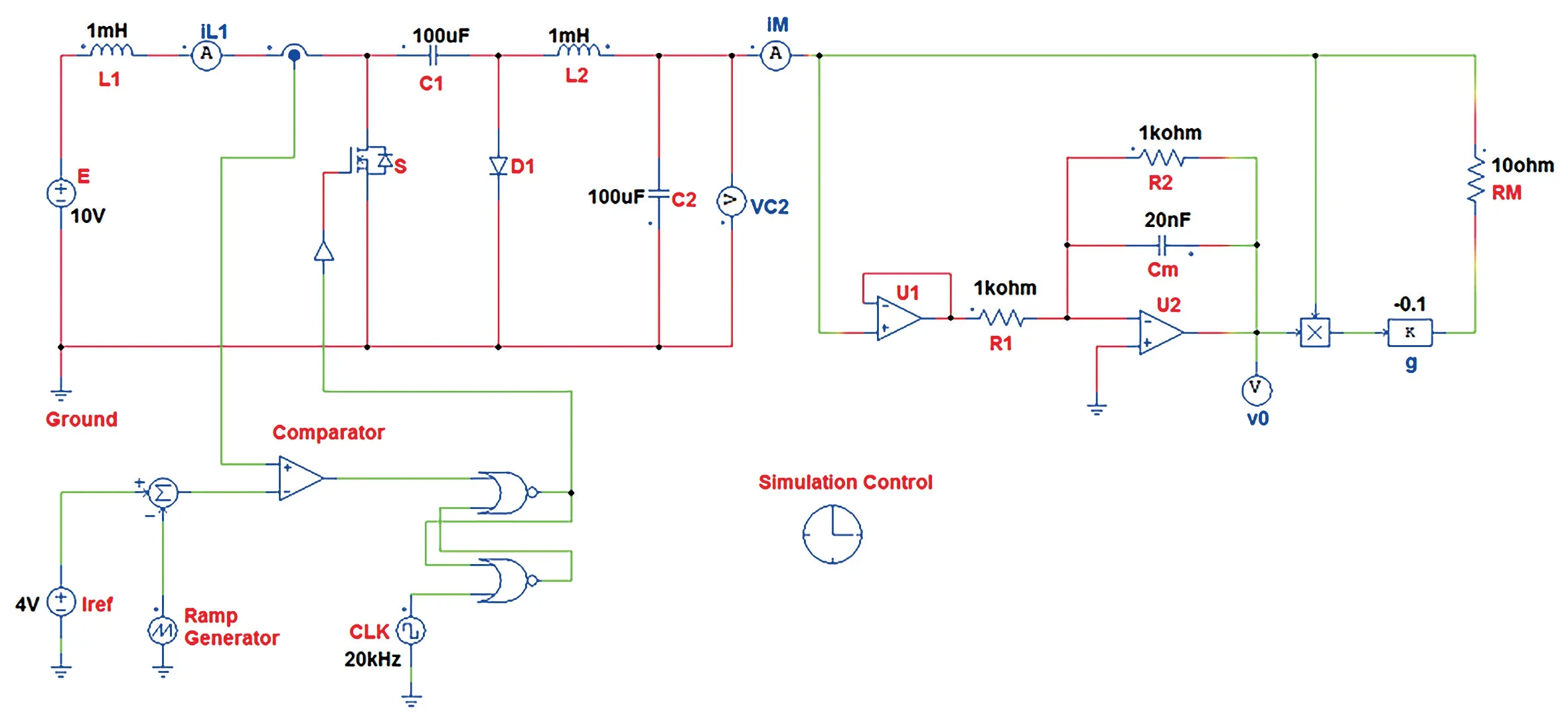
图12 峰值电流型忆阻Cuk 变换器PSIM 仿真电路图Fig.12 PSIM simulation circuit diagram of the peak current mode memristive Cuk converter

当无斜坡信号引入时,分别取Iref=4 V 和1 V,得到与图3 和图4 相对应的三个状态变量的电路仿真波形,如图13 所示。随后,图14 中参考电流Iref的取值分别为Iref=0.5 V,Iref=2.1 V,Iref=3 V 和Iref=5 V,相应的忆阻Cuk 变换器的工作状态分别为周期1、周期2、弱混沌以及完全混沌状态。电路仿真结果也表明,随着参考电流增大,忆阻Cuk 变换器的工作状态经历了周期、混沌等动力学行为。最后,在t=45 ms时,引入了不同斜率的斜坡补偿信号,得到了与图11对应的电感电流iL1的时序波形,如图15 所示。峰值电流型忆阻Cuk 变换器的PSIM 仿真结果与上述数值仿真结果一致,验证了理论分析的正确性。

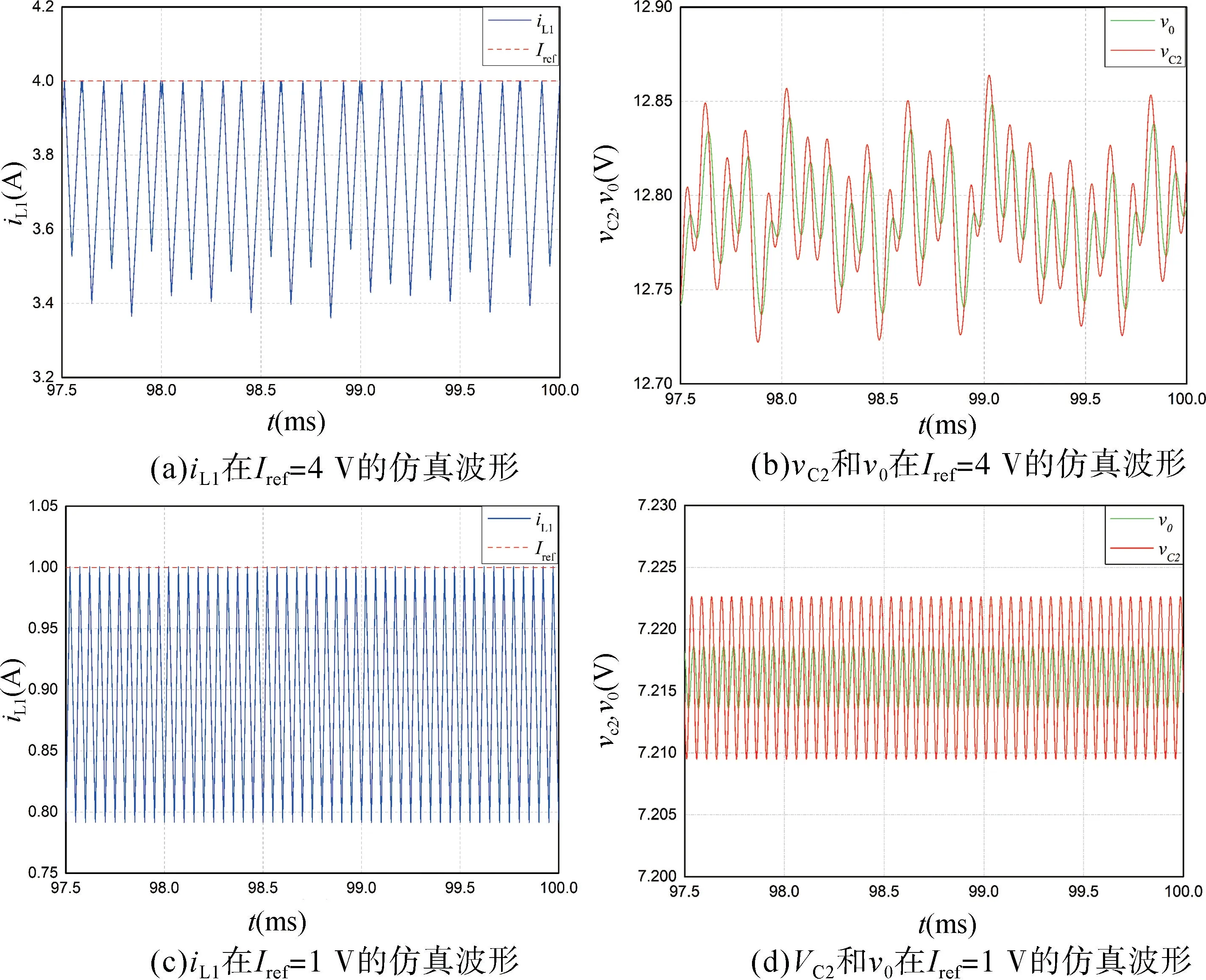
图13 峰值电流型忆阻Cuk 变换器的PSIM 仿真时域波形图Fig.13 PSIM simulated time sequences of the peak current mode memeristive Cuk converter

图14 峰值电流型忆阻Cuk 变换器随参数Iref变换时在iL1-v0平面上的PSIM 仿真相图Fig.14 For different values of the reference current Iref,PSIM simulated phase portraits of the peak current mode memristive Cuk converter in the iL1-v0plane

图15 引入mc后对电感电流iL1的镇定控制Fig.15 Stabilization control of the inductor current iL1after introducing mc

4 结论

由于DC-DC 变换器广泛应用在电力电子领域,与此同时,忆阻器作为新的基本电路元件将来也可能在电子电路中被广泛使用。因此,本文通过用一个压控忆阻负载替换Cuk 变换器上的传统电阻,构建了一个新的五阶分段非线性系统。首先,建立了两种开关状态下系统的数学模型,并利用Matlab 仿真发现对于给定的电路系统参数,变换器存在着复杂的动力学行为,包括混沌、周期、倍周期分岔和边界碰撞分岔。其次,通过忆阻负载与电阻负载的分岔图比较得到带忆阻负载的Cuk 变换器具有更大的稳定工作区间。同时,根据能量守恒原理得到了变换器关于相关参数的稳定运行参数域估计表达式。随后,通过引入斜坡补偿信号,对处于混沌状态的变换器进行镇定控制,消除变换器电路的不稳定性。最终,通过PSIM 电路仿真进行验证,验证了系统的正确性和可实现性,为忆阻器未来应用在电力电子领域提供了一定的理论依据。