基于矩量法非对称平行耦合微带线滤波器的设计

(景德镇陶瓷大学机电学院,江西景德镇 333403)

随着有线、无线通信技术的发展,微波滤波器在雷达技术、卫星通信、电子对抗、通讯安全等领域得到广泛应用。微波滤波器的作用是筛选不同频率的信号,允许系统指定的信号通过,过滤干扰信号。在某些领域中,微波滤波器的性能对整个系统有决定性的作用。

滤波器发挥着日益重要的作用,因此如何精确高效地设计性能优良的微波滤波器得到大量研究。在此背景下各种电磁仿真软件相继问世,为设计优化滤波器提供了多种选择,但是选择不当会将简单问题复杂化。电磁仿真软件有各自的特点,例如 ADS(Advanced Design System)仿真效率高,优化效果好,但是仿真优化过程在相对理想条件下,导致仿真结果与实际情况有较大差异。版图仿真效率低于ADS,但是其仿真准确性优于ADS,与HFSS(High Frequency Structure Simulator)相比仿真准确性有所不及。HFSS仿真结果精确,但是算法复杂,效率较低。因此如何合理的使用仿真软件是能否精确、高效设计滤波器的关键。

平行耦合线滤波器因具有相对带宽大、与射频电路匹配度高等优点,而得到了深入的研究[1-9],其主要研究方法有:软件分析法[1-8]、传输线理论分析法[9],本文选择软件分析法。文献[1-2]设计的滤波器通带宽、带内损耗小,但是通带反射较差,由于其优化全程在HFSS 完成,因此这种方法耗时,效率低。文献[3]利用ADS 设计了一种五阶平行耦合线滤波器,带内损耗小。文献[4-5]所设计的平行耦合线滤波器带内损耗小,但是滤波器选择性较低。文献[6]制作了一种四阶平行耦合微带线带通滤波器,其设计过程在ADS 中优化在版图中验证,若不符合要求则返回ADS 再次优化,其过程十分繁琐耗时。文献[7-8]阐述了一种基于ADS 高效设计平行耦合线带通滤波器的方法,但是这种方法依赖ADS 的自动优化,只适用于粗模型仿真得到初始结构参数,若要制作实物,后期仍需要大量时间优化。上述文献所设计的平行耦合线滤波器存在通带反射差、阻带选择性较低、优化方法不当等问题。

为了提高优化设计滤波器的精确性、效率与阻带选择性,本文通过合理的使用电磁仿真软件,在保证精确性的前提下,提高设计优化滤波器的效率与性能。并设计优化七阶平行耦合微带线滤波器验证,具体措施如下:一是采用非对称结构来获得更好的通带反射;二是采用矩量法与ADS 联合仿真优化提高设计优化效率,在版图中建模,在ADS 中优化,只在HFSS 中进行验证与微调,保证精确性的前提下,提高设计优化效率;三是增加滤波器的阶数,改善其选择性。

1 设计过程

1.1 耦合微带线结构参数的计算

本文中设计一个七阶平行耦合微带线带通滤波器,选择切比雪夫低通滤波器原型,如图1 所示。滤波器的技术指标为:中心频率f0=4.8 GHz,带宽(1.2±0.2) GHz,带内衰减≤2 dB,端口反射损耗≥25 dB,3.4 GHz 以下和6.2 GHz 以上的阻带衰减大于50 dB。选择基板厚h=1 mm,相对介电常数εr=2.7。设计步骤如下。

图1 低通滤波器原型Fig.1 A low pass prototype

(1) 计算归一化频率:

式中:ω0为中心频率;ωs为带外频率;ωh、ωl分别为通带上边频与下边频。选择0.1 dB 波纹的切比雪夫低通滤波器原型,查衰减曲线得N=7,可以满足阻带衰减要求。查表得归一化元件值g0=g8=1.00,g1=g7=1.81,g2=g6=1.42,g3=g5=2.10,g4=1.57。

(2)计算导纳变换器的导纳值Ji,i+1[10]:

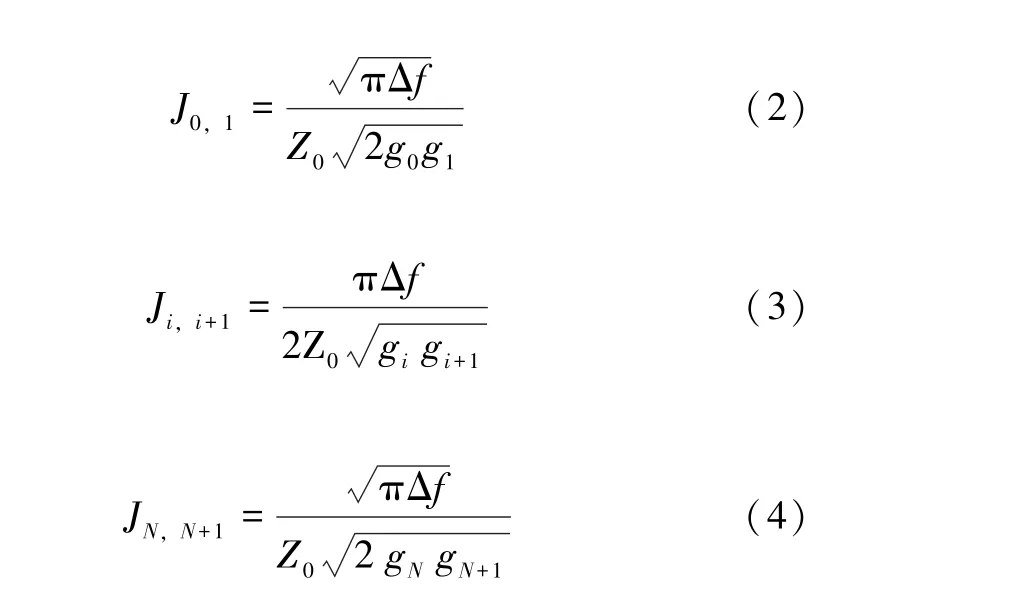
式中:Δf为相对带宽;Z0是端口的阻抗。

(3) 计算各段耦合线的偶模、奇模的特性阻抗Zoe、Zoo:

式中:Z0=50 Ω。

(4) 根据基板的参数和奇偶模阻抗,利用ADS 中Line Calc 进行计算,计算结果列于表1 中,wi、si、li(i=1,2,…,8)分别为相应谐振器的宽度、间距、长度,其原理图如图2 所示。

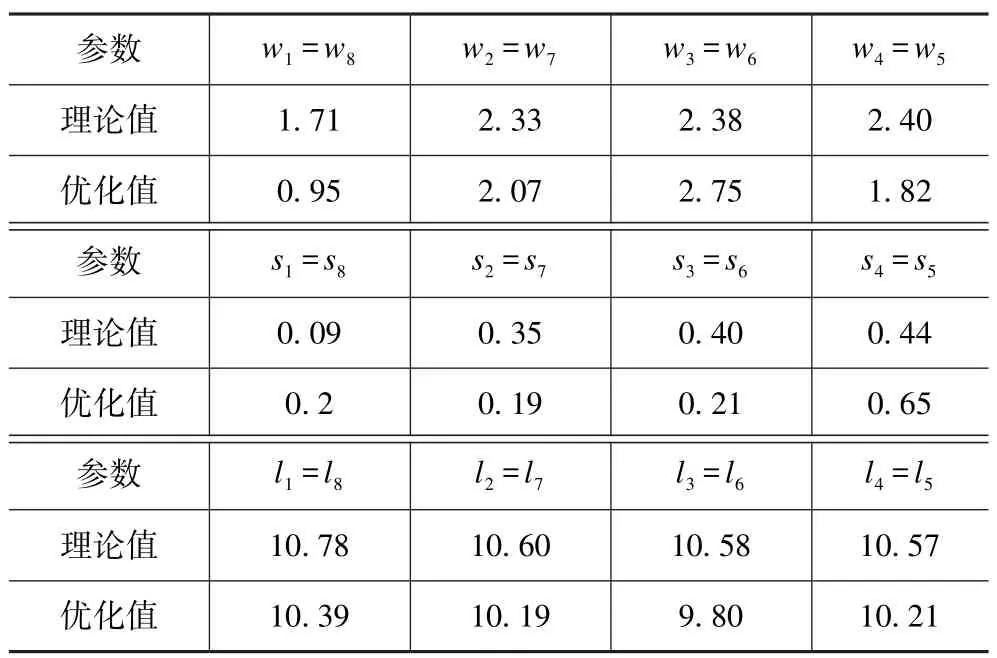
表1 ADS 中滤波器结构参数的理论值与优化值Tab.1 Theoretical and optimal values of filter structural parameters in ADS mm

图2 七阶平行耦合微带线带通滤波器原理图Fig.2 Schematic diagram of seventh-order parallel coupled microstrip line bandpass filter

1.2 滤波器的仿真与优化

以表1 中的理论结构参数在ADS 中建模如图3 所示,并对此模型仿真,仿真结果如图4 所示,其通带较理论值窄,反射损耗差,不符合设计要求,因此要对其优化。

采用ADS 自带的优化功能进行优化,优化后的结构参数也列于表1 中,优化后的波形如图4 所示。通过图4 对比可以看出,优化后的通带与反射曲线均符合设计要求。将优化后的结构参数代入HFSS 验证,仿真波形如图5 所示,由图5 观察得HFSS 与ADS 仿真结果存在差异,尤其是反射损耗与ADS 仿真结果不符。这是ADS 原理图仿真没有考虑到不相邻微带线之间的耦合所造成。

图3 滤波器在ADS 中仿真模型Fig.3 Simulation model of filter in ADS

图4 滤波器在ADS 优化前后的S 参数Fig.4 The S-parameters of filter in ADS before and after optimization

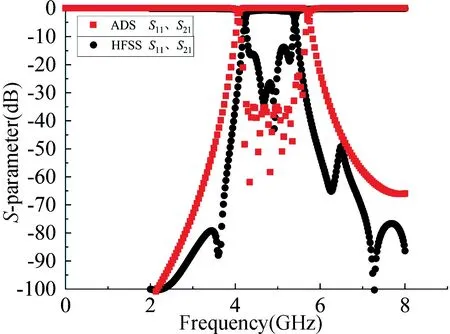
图5 ADS 仿真结果与HFSS 仿真结果Fig.5 The simulation results of ADS and HFSS

HFSS 精度高,但是算法复杂,耗时多,为了提高优化效率,采用版图和原理图联合仿真优化。在版图中建模,如图6 所示,在ADS 原理图中进行优化仿真,如图7 所示,图中的7pole 是图6 的版图模型,优化结果如图8 所示。

图6 七阶平行耦合微带线带通滤波器版图模型Fig.6 Layout model of seventh-order parallel coupled microstrip line bandpass filter

图7 ADS 中版图与原理图联合仿真Fig.7 Layout and schematic joint simulation in ADS

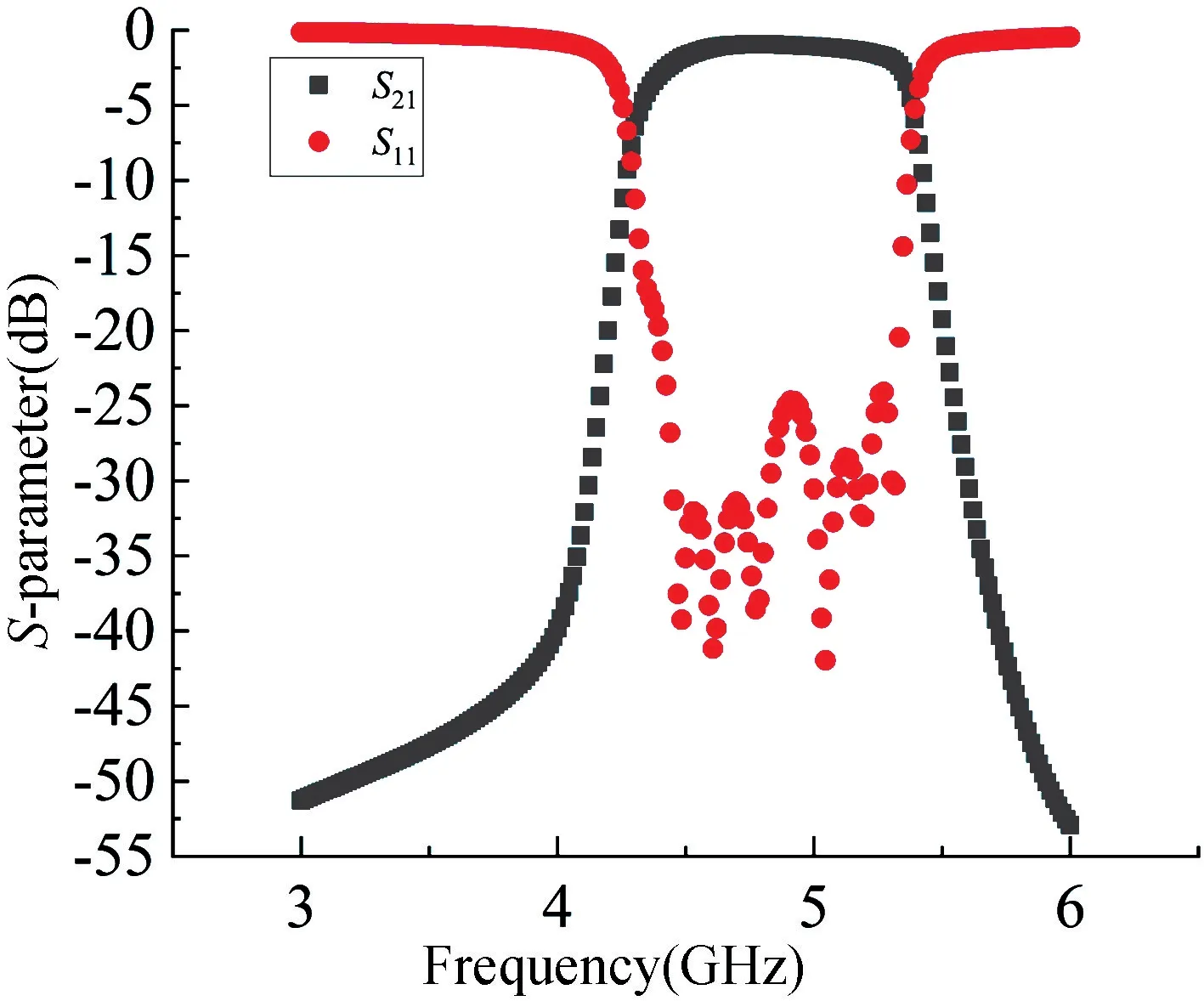
图8 ADS 中版图优化仿真结果Fig.8 Layout optimization simulation results in ADS

将优化后的结构参数放到HFSS 中进行验证,如图9 所示,性能基本达到要求,仅需微调。版图仿真是基于矩量法,而HFSS 仿真是基于有限元法,因此两者仿真会有所差异。版图优化仅仅只需要2 h 即可达到要求,而HFSS 中仿真一次就需要12 min,优化所需时间长,显然版图优化仿真省时,效率高。

在HFSS 中对参数进行微调时发现:li影响中心频率,随着li的增大,中心频率变小,wi影响其损耗,si影响其带宽,并且随着si的增大,带宽变窄。在优化过程中若采用对称结构很难达到预期要求,反射损耗一直达不到理想要求,于是采用非对称结构,对参数进行微调。采用非对称结构并运用上述规律,对滤波器进行优化,考虑制作工艺,将参数精度调整到0.01 mm,结构参数如表2 所示。从表2 可以看出,滤波器的结构不完全对称,即w1≠w8,w2≠w7,…,l3≠l6。仿真结果如图10 所示,滤波器已达到设计要求,并且获得比较好的性能。综上所述,采用不对称结构可以提高滤波器的反射性能。

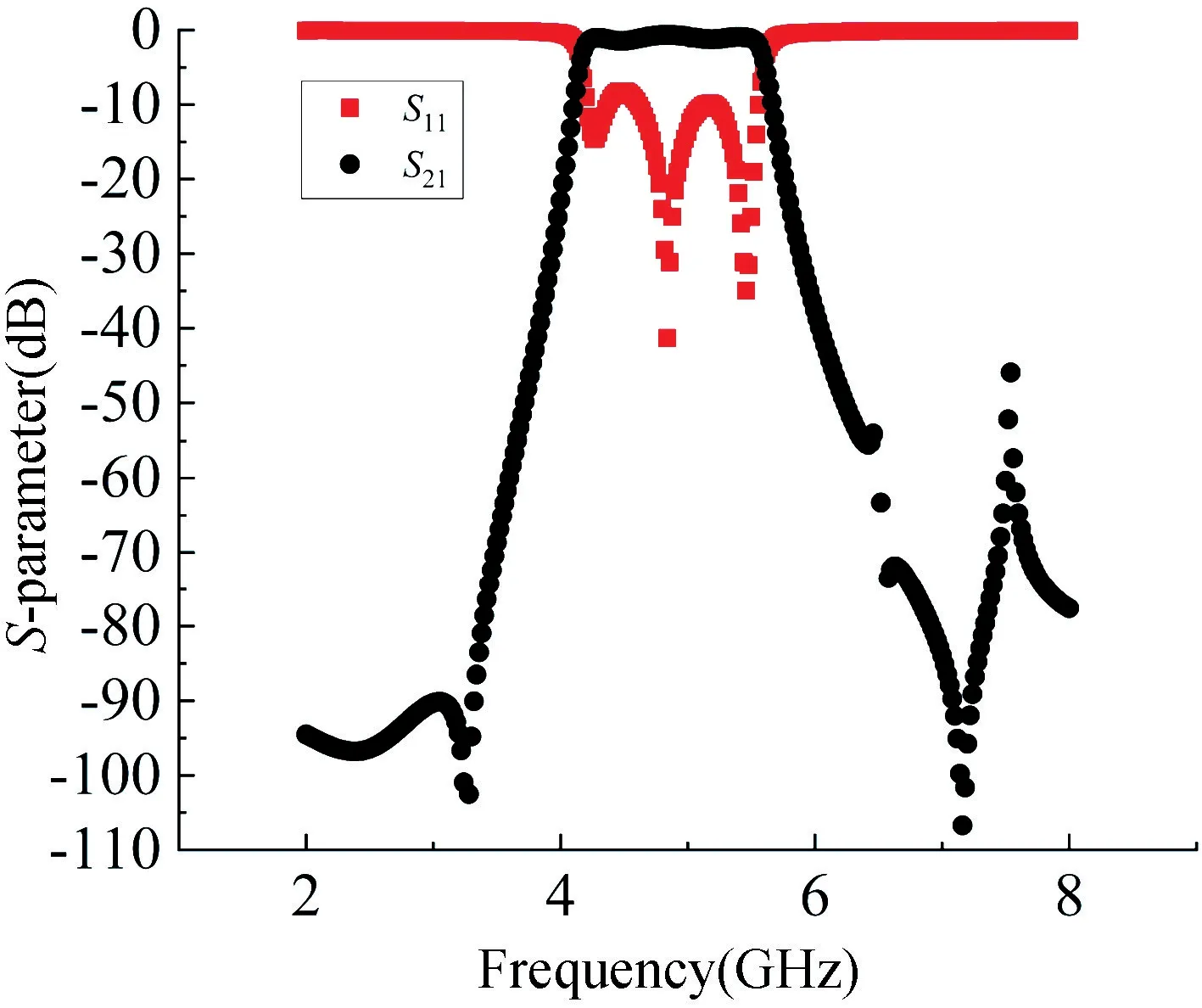
图9 版图优化后HFSS 验证结果Fig.9 HFSS verification results after layout optimization

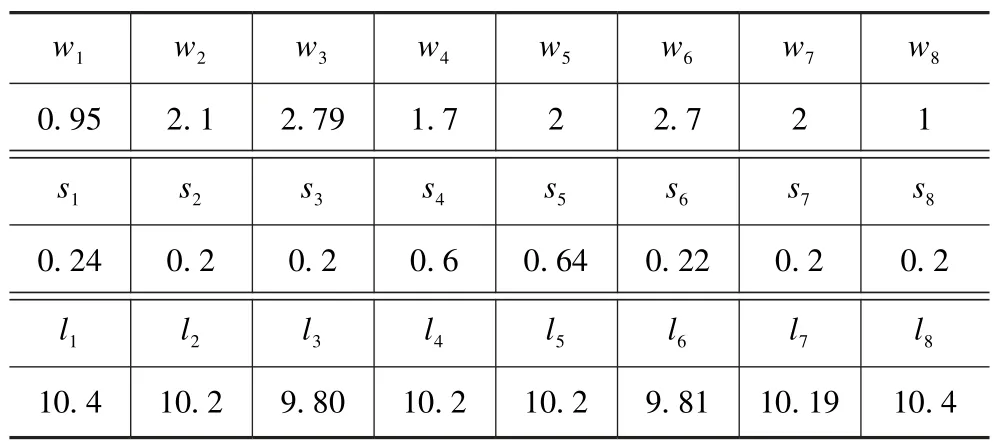
表2 优化后各结构参数Tab.2 The optimized structure parameters mm

图10 HFSS 优化后仿真结果Fig.10 Optimized simulation results of HFSS

2 实物的制作与测量

以表2 的结构和尺寸制作实物,实物照片如图11所示。用网络分析仪Agilent E5071B 进行测量,测量数据如图12 所示,中心频率为4.86 GHz,带宽BW=1.2 GHz,插入损耗为1.2 dB,反射损耗大于25 dB,3.4 GHz 以下和6.2 GHz 以上的阻带衰减均大于50 dB。测量结果与仿真结果相比,除中心频率偏高外,其余均相符。

图11 七阶平行耦合微带线带通滤波器实物照片Fig.11 The photo of the seventh-order parallel coupled line bandpass filter

图12 七阶平行耦合线带通滤波器实测曲线Fig.12 The measured curves of the seventh-order parallel coupled linebandpass filter

表3 列出了本文的测量结果与其他文献所报道的结果,从表中看出,本文的滤波器的插入损耗小、反射特性好,矩形系数高。

表3 与其他平行耦合微带线带通滤波器性能对比Tab.3 Compared with other parallel coupled microstrip line bandpass filters

3 结论

提出一种滤波器的设计方法:在版图中建立模型,将模型放到ADS 原理图中进行仿真优化,然后在HFSS 中进行验证微调。该方法结合ADS 原理图仿真优化的省时高效与版图仿真的准确性,大大提高了滤波器设计与优化的效率。并用此方法设计制作了七阶平行耦合微带线滤波器,实验验证了矩量法的可行性与高效性,且验证了非对称结构对改善滤波器的性能有良性作用。该方法与结构可应用到其他微波元器件的设计中。