基于磁通补偿的串并联混合型电能质量控制器

2021-04-28陈先锋王庭康卓定明李冠桥黄秉开龚杰李达义

广东电力 2021年4期

陈先锋，王庭康，卓定明，李冠桥，黄秉开，龚杰，李达义

(1. 广东电网有限责任公司惠州供电局，广东惠州 516000；2.强电磁工程与新技术国家重点实验室(华中科技大学)，湖北武汉 430074)

随着太阳能发电、风能发电等可再生分布式能源(distributed generation，DG)、高压直流输电系统(high voltage direct current transmission，HVDC)、电力电子装置等不断发展，电力电子技术成为新能源接入以及能源互联网的核心技术之一，电力系统已逐步发展成为高度电力电子化的电力系统[1-3]。而这些典型的非线性负载势必会引起谐波污染，给电力系统带来严重的电能质量问题，影响系统的安全稳定经济运行，也影响周围电力设备的安全稳定运行[4-7]。

为了解决所面临的各种电能质量问题，有源电力滤波器(active power filter，APF)、统一电能质量控制器(unified power quality controller，UPQC)、静止无功补偿发生器(static var generator，SVG)等电能质量治理设备得到了有效的发展[8-15]。其中，通过对基波和谐波分量呈现不同的阻抗，基于磁通补偿技术的APF实现了对谐波的隔离作用，能够解决部分电能质量问题[16]。文献[17]提出了基于磁通补偿控制的并联型APF，通过检测变压器一次侧绕组的谐波电流来控制变压器，使其对谐波电流呈现低阻抗，对基波电流呈励磁阻抗，从而为谐波电流提供了低阻抗通路；但是，这种方式受电力系统内阻抗影响较大，只能运用在内阻大的高压系统中，难以应用到内阻较低的低压系统中。文献[18]将基于磁通控制的APF推广到了可调电抗器，并且提出了简化无源电力滤波器的设计方案；但是，对于各次谐波来说，该支路的阻抗并非取得了最佳值，无源提供的低阻抗通路并不是理想的。通过分析相关文献[19]可知，当前基于磁通补偿的APF存在的共同缺陷是：串联时无源支路不能对所有次系统提供理想低阻抗通路，并联时滤波效果受系统内阻抗影响很大；并且，两者都难以做到既能很好滤除谐波，又能动态补偿无功。

针对以上问题，本文提出基于磁通控制的电能质量控制器。它由1个串联在电源和非线性负载之间的串联变压器、1个并联在负载两端的并联变压器，以及2个变压器二次侧的逆变器及其控制结构、直流侧电容组成。本文对串联、并联变压器实施不同的磁通控制方式，以分别在整个系统中表现出不同的特性。就串联变压器而言，逆变器向变压器二次绕组注入可控的基波电流，即：在电网系统正常时，全部注入基波以使变压器呈现大谐波阻抗；而在电网发生过流故障时，调节注入基波大小以呈现大的基波阻抗限制故障电流。就并联变压器而言，一方面针对谐波分量呈现低阻抗以实现更好的滤波效果，另一方面对基波分量呈现可调阻抗完成动态无功补偿[20]。本文对所提的基于磁通补偿控制的电能质量控制器进行理论分析，并进行软件仿真分析，验证该方案滤除谐波、限制故障电流和动态补偿无功等功能的有效性。

1 电能质量控制器系统结构

图1为本文提出的基于磁通补偿控制的电能质量控制器结构图，其中：Us为系统电源电压；Zs为电源的内阻抗；Is为流经串联变压器一次侧绕组的电流；IL为非线性负载的电流；T1为串联线性变压器，串联在非线性负载和电源线路之间；T2为并联线性变压器，与非线性负载相并联，其中变压器铁心都设计有一定气隙，以保证始终能够工作在磁感应强度与磁场强度关系曲线(B-H曲线)的线性段，不发生磁饱和；Lf1、Lf2均为电压源型逆变器的输出滤波电感器；C3、L3分别为3次单调谐无源电力滤波器的电容器、电感器；RL、LL分别为非线性负载中所接电阻器、电感器，即非线性负载为晶闸管相控整流的阻感负载；C为逆变器直流侧的电容器，用以提供稳定的直流电压Udc；If1、If2分别为串联、并联变压器二次侧出逆变器所产生的电流；IT2为并联变压器一次侧绕组电流；SPWM为正弦波脉冲宽度调制，sinusoidal pulse width modulation的缩写。

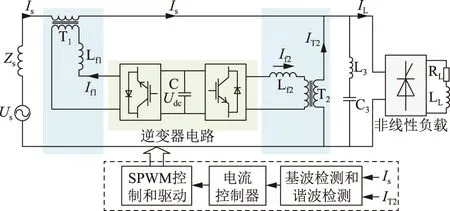
图1 基于磁通补偿控制的电能质量控制器系统结构Fig.1 Block diagram of the power quality controller based magnetic flux compensation

在系统控制中，根据检测到的电流Is、IT2，采用常用的瞬时无功功率理论来提取其中的基波电流信号和谐波电流信号，作为指令电流信号；设计合理的电流跟踪控制器来跟踪指令电流信号，对指令信号与实际产生的电流发生的偏差进行控制，以减小静态误差；再控制电压源型逆变器，以产生对应的补偿电流，分别注入到串联变压器、并联变压器二次侧绕组中。从而，串联变压器对基波电流分量呈近似为0的阻抗，且故障时表现为高阻抗以限制故障电流；对谐波电流分量呈励磁阻抗，起到谐波隔离的作用。并联变压器为谐波电流提供低阻抗通路，对基波分量呈现连续无级可调的电抗，因而可以实时补偿感性无功电流，以提高系统的功率因数。

同时，为了使电压源型逆变器直流侧电压稳定在设定值，可采用储能电容通过相应的控制器来调节直流电压，以减小稳态误差[21]。除了这种方法之外，还可以在直流侧接蓄电池，通过控制逆变器使电压稳定；或者从电力系统取电，经过整流稳压之后得到稳定的直流电压[22-24]。对于直流侧电压控制以及串并联部分的功率优化配置，本文不做具体赘述，后续研究将进一步分析，下面简要分析一下直流电源需要输送的有功和无功功率。

在电能质量控制器稳态工作的时候，对于不同的工况而言，电网，负载，串、并联变换器四者之间的功率潮流是动态平衡的。其中，串联部分有功功率P1和无功功率Q1分别为：

式中：ΔU为变压器T1端电压；θΔ为变压器T1端电压与Is间的夹角。另外，为了实现串联部分的有功功率需求，并联部分传递有功功率P2和无功功率Q2应分别为：

式中：UL为负载的电压；θ为负载电压UL与负载电流IL间的夹角。

理想的控制条件下，不计线路损耗，交流电网输入有功功率Ps等于负载吸收的有功功率PL，即Ps=PL。结合以上各式，令k=UL/Us，可以得到串联和并联部分有功功率如下：

P1=(UL-Us)Is=(UL-Us)Ps/Us=

Ps(UL/Us-1)=Ps(k-1)，

P2=UL(ILcos φ-Is)=

PL-PsUL/Us=Ps(1-k).

式中cos φ为功率因数。

由以上各式可以看出，两者功率相反。具体来说，若P1为正，串联部分输出有功功率，此时P2为负，并联部分输入有功功率；若P1为负，串联部分输入有功功率，P2为正，并联部分输出有功功率。下面给出一种理想条件下系统稳态运行的潮流分析图(如图2所示，图中数值均为标幺值)，图中：Qs为交流电网输入无功功率；QL为负载吸收的无功功率；PT为电网线路经过串联变压器后传输的有功功率；i1为串联变压器一次侧电流瞬时值；is为Is的瞬时值；ip为主电路有功电流；iLq为流过电能质量控制器并联部分的无功电流；Δip为并联部分吸收的有功电流；iL-q、iL-p分别为负载电流中的无功分量和有功分量。

图2 理想条件下系统稳态运行系统的潮流分析Fig.2 Power flow analysis of steady operation system under ideal conditions

此时，电力系统稳态运行(Us等于额定电压UN，令UN=UL=1.0)，串联部分和并联部分既不发出也不吸收有功功率，而并联部分提供负载无功功率。

2 工作原理分析

本文所提出的基于磁通补偿的电能质量控制的变压器和逆变器结构如图3所示，图中：AX、ax分别表示变压器一次侧绕组、二次侧绕组标号；W1、W2分别为变压器一次侧、二次侧绕组的匝数；u1、u2分别为一次侧、二次侧的绕组端口电压瞬时值；M为变压器一次侧与二次侧的互感。变压器设计有气隙，保证变压器能够工作在线性区间，不会因磁饱和导致励磁阻抗减小。

图3 变压器和逆变器结构框图Fig.3 Block diagram of transformer and inverter

其中，变压器可以用如图4所示的等效T型电路来表示，图中：R1、R′2分别为变压器一次侧绕组电阻、二次侧绕组电阻(折算到一次侧)；L1σ、L′2σ分别为变压器一次侧绕组漏感、二次侧绕组漏感(折算到一次侧)；Z1=R1+jωL1σ为变压器一次绕组漏阻抗；Z′2=R′2+jωL′2σ为变压器二次绕组漏阻抗(折算到一次侧)；Rm、Lm分别为变压器铁心损耗等效电阻、励磁感抗；Zm=Rm+jωLm为变压器励磁阻抗；I1、I′2分别为变压器等效电路上的一次侧绕组电流、二次侧绕组电流(折算到一次侧)。U1、U′2分别为变压器一次侧电压、二次侧电压(折算到一次侧)；E1为变压器励磁电动势。

图4 变压器等效T型电路Fig.4 Equivalent-T circuit of transformer

由图4所示的变压器T型等效电路，可以推导得到变压器电压方程式如下：

(1)

可通过检测变压器一次侧绕组电流形成指令电流信号，控制逆变器，以产生跟踪电流并注入到二次侧绕组中，从而使变压器对不同频率的电流分量呈现不同的阻抗，实现谐波隔离和无功补偿的作用[25]。

2.1 串联变压器控制模式

检测串联变压器T1一次侧绕组流过的电流I1，采用瞬时无功功率理论谐波检测方法来提取I1中的基波电流信号I1(1)。文中变量符号用下标(1)表示基波信号，用下标(n)表示n次谐波信号。注入到变压器二次侧绕组的电流控制方程式为

I′2=-αI1(1)，

(2)

式中α为基波电流控制系数。

联立式(1)、(2)，针对一次侧绕组基波分量而言，可以推导得到变压器一次侧绕组接入到系统中的基波等效阻抗ZAX(1)，

ZAX(1)=U1(1)/I1(1)=Z1+(1-α)Zm.

(3)

如果α=1+Z1/Zm，ZAX(1)=0。但是考虑到系统控制的稳定性问题，为保证系统能稳定运行，本文取α=1，此时基波等效阻抗

ZAX(1)=Z1.

(4)

式(2)中，当注入到二次侧的谐波电流分量为0时，就谐波分量而言，变压器二次侧绕组处于开路状态。同时，结合式(1)、(2)可知，变压器二次侧绕组接入到系统中的谐波等效阻抗

ZAX(n)=U1(n)/I1(n)=Z1+Zm.

(5)

分析式(4)、(5)可知，串联变压器所呈现的阻抗特性为：对基波电流分量呈现很小的一次侧绕组漏抗，其近似为0；对谐波电流分量呈现很大的励磁阻抗(Z1≪Zm)。因此，串联变压器能够利用很大的谐波阻抗来隔离谐波，使非线性负载所产生的谐波电流不流进电源侧，并且对基波电流分量不产生任何影响。

然而，当电力系统出现过电流故障时，串联变压器能够发挥故障限流器(fault current limiter，FCL)的作用。α能够在控制系统稳定条件下通过控制系统进行调节，使得变压器一次绕组呈现连续可调的阻抗，且当α<0时，该阻抗非常高。根据式(3)可知，变压器一次绕组等效阻抗与控制系数α成反比，具体关系见表1。因此，控制参数设定为α<0时，串联变压器阻抗

ZFCL≈ZAX(1)=Z1+(1-α)Zm≥Z1+Zm，

(6)

发挥了故障电流限制器的作用。

表1 控制系数与等效阻抗的关系Tab.1 Relationship between the equivalent impedance and control coefficients

根据以上分析串联变压器的控制模式，总的来说，由式(4)、(5)、(6)可知，该电能质量控制器的串联变压器一次绕组的等效阻抗特性可归纳为：

a)对于基波分量，基波电流系数α=-1，等效阻抗等于变压器漏抗，近似为0。

b)当电力系统发生过电流故障时，串联变压器会出现α<0的高阻抗，起到故障限流的作用。

c)串联变压器对谐波电流具有很高的励磁阻抗，起到谐波隔离器的作用。

因此，该电能质量控制器的串联变压器模块能在不影响电力系统正常运行的情况下，抑制谐波电流，同时在系统发生过流故障时起到故障限流器的作用。

2.2 并联变压器控制模式

提取并联变压器T2的一次侧绕组电流i1中的谐波分量和基波分量，利用电压源型逆变器向并联变压器二次侧绕组注入补偿电流i2(瞬时值)且满足

i2=-k1∑i1(n)-k2i1(1).

(7)

式中：k1为谐波控制系数；k2为基波控制系数。

同理，从AX端看，并联变压器n次谐波电压方程为

(8)

若k1满足谐波补偿条件为k1=1，并联变压器对谐波电流等效阻抗

ZAX(n)=Z1，

(9)

Z1可以忽略不计，对谐波电流呈现近似为0的阻抗。另外，变压器基波电压方程为

(10)

则并联变压器对基波等效阻抗

ZAX(1)=U1(1)/I1(1)=Z1(1)+(1-k2)Zm(1).

(11)

由式(11)可以得到变压器对基波等效阻抗ZAX(1)与基波控制系数k2之间的关系如图5所示。

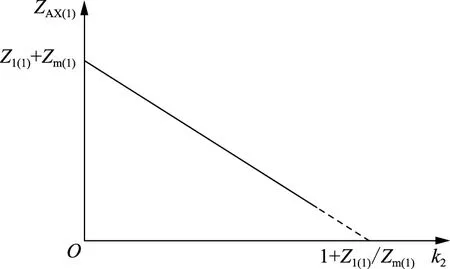
图5 并联变压器基波等效阻抗与基波控制系数的关系Fig.5 Relationship between the equivalent impedance and control coefficients of shunt transformer fundamental wave

由图5可知，通过实时调节基波控制系数k2的大小，就能实现并联变压器对基波电流呈现连续无级可调的阻抗，以补偿电力系统的无功功率。

因此，并联变压器的阻抗特性表现为：对谐波电流分量呈现近似为0的漏抗，起到提供谐波通路的作用；对基波电流呈现连续无级可调的阻抗，通过调节基波控制系数可补偿系统的无功功率。

3 系统等效电路与稳定性分析

在分析完串联变压器和并联变压器的控制模式之后，将整个电路按照基波和谐波分量化为等效电路，分析所提出的基于磁通补偿电能质量控制器的工作原理，以及进行稳定性分析。

3.1 谐波分量等效电路

图6为系统的谐波等效电路图，图中：Ush为系统电源背景谐波电压，本文暂不考虑此种因素，忽略背景谐波电压；Zsh、ZT1,h、ZT2,h分别为系统内谐波阻抗、串联变压器等效谐波阻抗、并联变压器等效谐波阻抗；Ish、IT2,h、ILh分别为流经电源谐波电流、并联变压器中谐波电流、阻感负载产生的谐波电流；ZPPF为无源电力滤波器阻抗。

图6 谐波等效电路Fig.6 Harmonic equivalent circuit

根据该谐波等效电路，可以得到

(12)

3.2 基波分量等效电路

根据前面串联变压器和并联变压器的不同控制模式分析可知，ZT1,h≫ZT2,h，则Ish≈0。并且，相对于利用无源电力滤波器提供低阻抗通路来说，这种采用并联变压器的方式对所有次谐波都能够呈现低阻抗，效果更好。

图7为系统的基波等效电路图，图中：Usf为系统电源基波电压；Zsf、ZT1,f、ZT2,f分别为系统内基波阻抗、串联变压器等效基波阻抗、并联变压器无级可调基波阻抗；Isf、IT2,f、ILf分别为流经电源基波电流、并联变压器中基波电流、负载基波电流；ZPPF,f为无源电力滤波器的基波阻抗。

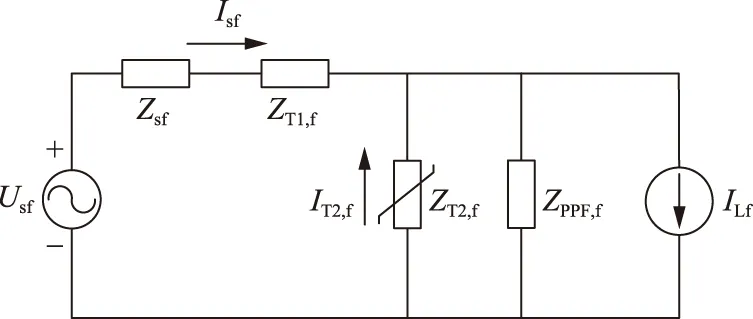
图7 基波等效电路Fig.7 Fundamental wave equivalent circuit

根据该基波等效电路，可以得到

(13)

通过无级连续调节IT2,f即可对电流Isf进行控制，配合无源电力滤波器，动态补偿无功功率。

3.3 系统稳定性分析

该电能质量控制器应用于实际系统中治理电能质量时，应当首先满足稳定性的要求，所以需要推导出该电能质量控制器模型分析的稳定性条件。

根据前面对串并联APF控制的具体分析可知，尽管两者检测的电流分量以及注入到变压器二次侧电流不一致，但是两者本质上是相同的，都是通过检测变压器一次侧绕组电流，注入补偿电流到变压器二次侧。因此，本文对该控制模式的APF进行稳定性分析，得到如图8所示的电能质量控制器结构框图。图8中：检测延时表示为一阶惯性环节Gdi(s)=1/(sTd+1)，s为拉普拉斯算子，Td为采样周期；PI调节器的传递函数GPI(s)=kp+ki/s，kp、ki为PI调节参数；GPWM为驱动及逆变环节的等效传递函数；kT、Lf分别为变压器变比、逆变环节输出滤波器电感值；K为控制系数，对于控制系数α、k1、k2，在控制系统稳定分析时用K统一表示。

考虑0.5个采样周期的开关延时，则GPWM(s)=KPWM/(0.5sTd+1)，KPWM为驱动及逆变环节的增益。考虑到系统开关频率很高，载波周期Td很小，所以可将(0.5sTd+1)(sTd+1)≈1.5sTd+1。整合PI参数、KPWM系数以及传感器比例系数，令k′p=kpKPWMkd，k′i=kiKPWMkd，kd为电流传感器增益。简化后的系统开环传递函数

(14)

由于在变压器等效电路中漏阻抗远小于励磁阻抗，即Z1≪Zm、Z′2≪Zm，且令k′p/k′i=Lm/Rm，k′=(k′ps+k′i)/Zm，所以可以对式(14)中的开环传递函数进一步化简。系统特征方程为1+Gopen(s)=0，具体为

可以写成a0s3+a1s2+a2s+a3=0，式中：

根据Routh判据可知，系统稳定条件为特征方程系数ai>0(i=0,1,2,3)，且a1a2>a0a3。显然，前一个条件都能够满足，后者条件如下：

由上式可知，当满足以上条件时，电能质量控制器系统是稳定的。

4 仿真实验与分析

为了验证所提出的基于磁通补偿的电能质量控制器的原理分析，在电路仿真软件PISM 9.0中建立了如图1所示的电路仿真模型。系统电源等效为110 V电压源和1个电感器串联，频率为50 Hz；串并联变压器变比均设置为1∶1；串联变压器短路阻抗为0.056 Ω，励磁阻抗为6.58 Ω；并联变压器短路阻抗为0.089 Ω，励磁阻抗为10.48 Ω；系统无源支路为3次谐振型LC滤波器，其中C3的电容值C3=1 200 μF，L3的电感值L3=0.939 2 mH；串联有源滤波基波控制系数α为-1；并联有源滤波基波控制系数k1为-1，谐波控制系数k2连续可调；谐波负载选用接有阻感型负载的二极管不控全桥整流电路。

图8 该电能质量控制器的结构控制框图Fig.8 Control block diagram of the proposed power quality controller

由于本文侧重点在于电能质量功能的实现，为了便于简化分析以及减少文章篇幅，本文将不涉及串并联电能质量装置的功率流优化配置，逆变器直流侧母线电压直接选用直流电源代替，具体串并联之间的有功、无功功率推导与仿真数据在后续文章中进行详细阐述。

根据所设计参数，利用PSIM软件搭建好仿真电路，对本文提出的基于磁通补偿电能质量控制器进行仿真实验验证。

4.1 谐波隔离功能验证

在未接入该电能质量控制器和无源电力滤波器时，电源电路中流过的负载电流和电源电压的仿真波形如图9所示，功率因数为0.904(感性)，负载电流畸变率为45.35%。

图9 未接入电能质量控制器时电压、电流波形Fig.9 Voltage and current waveforms without the proposed power quality controller

为了能够更加清晰地体现本文提出的电能质量控制器相对于常规的磁通补偿型串联或并联APF在谐波抑制功能上的优势，本文在参数相同的情况下，分别进行了4种情况对比仿真分析，这4种情况分别为基于基波磁通补偿的串联型APF、基于谐波磁通补偿的并联型APF、不含无源滤波支路的本文所提电能质量控制器，以及本文提出的磁通补偿串并联型电能质量控制器。观察这4种滤波方案滤波之后电源电流Is和负载电流IL的波形，并且对其进行快速傅里叶变换(fast Fourier transform，FFT)量化分析，滤波效果以及FFT分析分别如图10(a)—(d)所示。相对于在谐波抑制之前电源电流的总谐波畸变率45.35%，图10中这4种方案滤波后电源电流总谐波畸变率分别为2.78%、3.47%、1.47%和0.50%。

对比FFT分析得到的数据可知，本文提出的串并联型电能质量控制器能够达到最好的滤波效果，不含无源滤波支路的本文所提电能质量控制器的滤波效果次之，其后分别是基于磁通补偿的串联型APF和并联型APF。这是因为在本文所提出的磁通补偿的串并联型电能质量控制器中，串联部分对所有次谐波呈现高阻抗，并联部分对所有次谐波呈现低阻抗，从而优化了常规的基于磁通补偿的串联型APF和并联型APF的滤波效果。即本文方案解决了基于磁通补偿的串联型APF需要无源滤波支路提供低阻抗通路时不能对所有次谐波呈现低阻抗的问题，同时解决了基于磁通补偿的并联型APF滤波效果在很大程度上取决于电网系统内阻抗大小的问题。

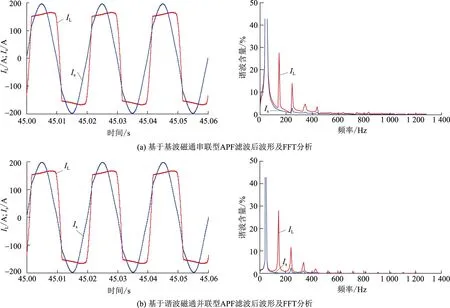
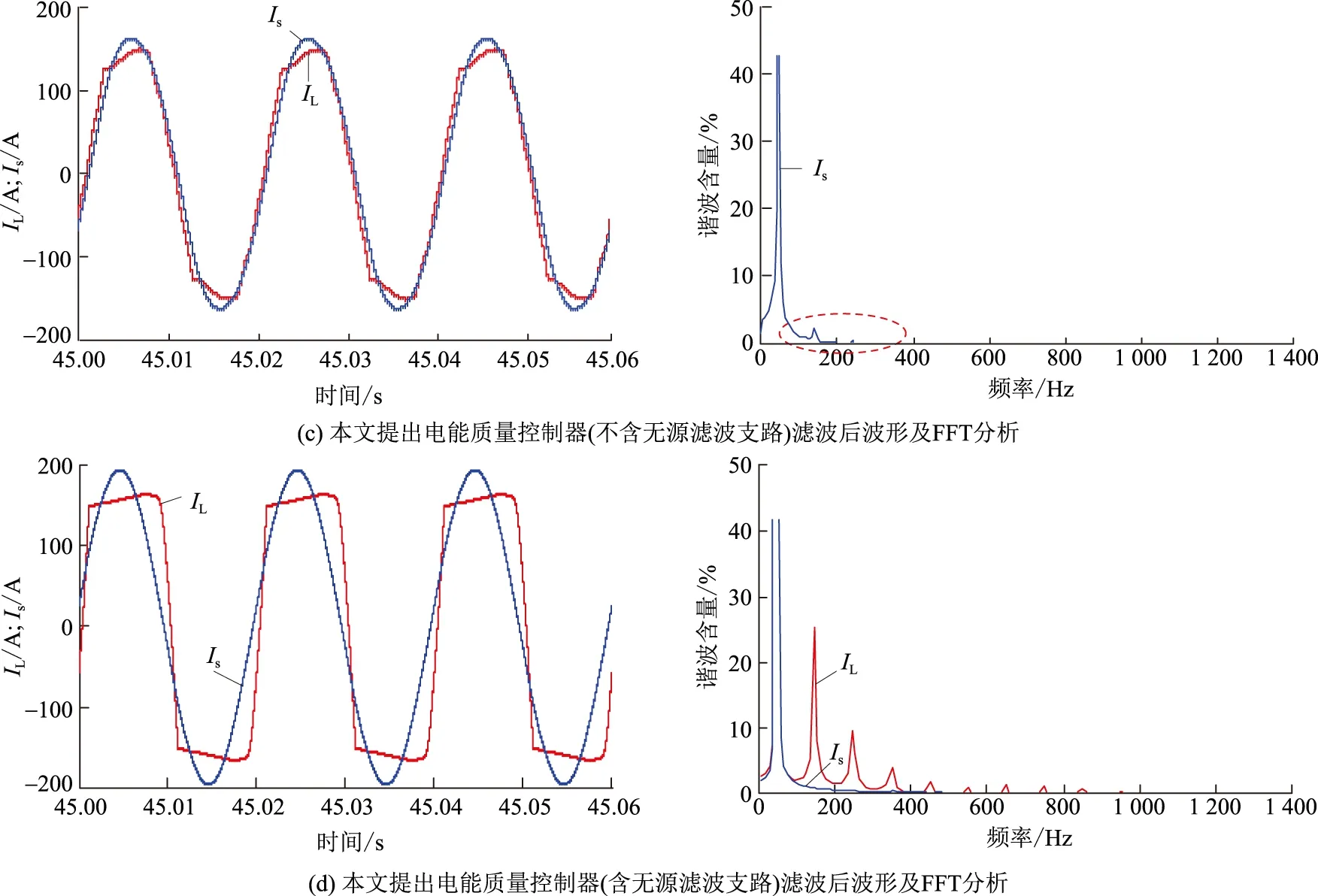
图10 4种不同情况滤波效果对比Fig.10 Filtering effect comparisons of four different harmonic suppression methods

另外，比较图10(c)与图10(a)、(b)的FFT频谱图3次以上谐波含量可知，本文方案能够对所有高次谐波呈现低阻抗，实现了所有次谐波的滤波，尽管不含单调谐无源滤波支路，依旧取得了非常好的滤波效果；比较图10(c)与图10(d)的FFT频谱图可知，图10(c)中Is的3次谐波含量大于图10(d)中Is的3次谐波含量，这是由于后者含有3次单调谐无源滤波支路，对3次谐波分量阻抗近似为0。对于无源滤波支路需要补充说明的是，本文引入3次谐波无源电力滤波器不仅仅是为了提高滤波效果，更多的是配合并联APF的基波阻抗，综合实现无功功率的补偿作用。

4.2 故障电流限制功能验证

在仿真过程中时间为25.0 s时设置系统发生过流故障，该串并联型电能质量控制器在时间26.0 s时起故障限流器的作用，串联变压器的基本电流控制系数α设为0.5，即串联变压器的一次绕组阻抗表现出非常高的阻抗，以限制系统故障电流。图11显示了该电能质量控制器在故障限流器状态下工作时的电流波形。在时间25.0 s时故障发生，导致系统电流迅速增加。然后，在时间26.0 s时，通过调节串联变压器一次绕组基波阻抗，系统电流被限制在安全水平。

图11 发挥故障限流器作用时限流效果波形图Fig.11 Current limiting waveforms with FCL

4.3 无功补偿功能验证

基波控制系数k2取0、0.66、0.8这3种情况下的系统电压和电源电流的波形如图12所示。通过计算分析可知，这3种情况下的功率因数分别为0.895(容性)、0.998(感性，接近单位功率因数)、0.908(感性)。接入电能质量控制器前，功率因数为0.904，接入电能质量控制器后功率因数为0.998(k2=0.66)，与接入前相比，功率因数有了很好的改善；因此，通过调节并联变压器控制系统中的基波控制系数k2，可以无级连续调节无功功率。

图12 不同基波控制系数下无功补偿效果(k2=0；k2=0.66；k2=0.8)Fig.12 Reactive power compensation effects under different fundamental wave control coefficients(k2=0; k2=0.66; k2=0.8)