基于四线圈的动态无线输电的位置检测

杨金明，邓梓颖，陈渊睿，孙杰杉

(华南理工大学 电力学院，广东 广州 510641)

电动汽车因具有清洁、高效以及噪音低、维护方便等优点，逐渐成为可替代传统汽车的交通工具[1-4]。然而电动汽车在实际应用中仍然存在许多问题，其中一个关键问题就是电动汽车供电。由于蓄电池的充电时间长，且电池能量密度较低[5]，与传统汽车相比，电动汽车能量获取过程所需时间更长，持续行驶时间更短[6-7]。要减少充电次数，延长电动汽车的续航里程，需要增加蓄电池体积，这不仅会增加电动汽车的重量，而且会增加蓄电池的制作成本[8]。在这一背景下，电动汽车的动态无线输电成为解决供电问题的可能方案[9]。

当前研究的基于磁耦合谐振的道路无线输电系统主要有2种[10]：一种是轨道无线输电，其发射侧是一体的电流导轨[11]，如图1(a)所示；另一种是分布线圈无线输电，其发射侧是多个独立的发射线圈[12]，如图1(b)所示。这2种无线输电系统面临的共同问题是：当接收线圈相对于发射导轨或线圈发生左右偏移时，二者之间的互感下降，从而导致电动汽车获取的电能减少，系统效率下降[13]。为了解决这一问题，一些文献采用改变发射线圈或接收线圈结构的方法，使系统有更大的偏移容忍度[14-16]；另一些文献则利用磁阻传感器或感应线圈，检测并校准电动汽车的位置，使接收线圈尽量对准发射线圈[13,17]。文献[18]提出的系统中设置了多条发射导轨，根据发射侧的电压、电流相位差变化，决定切换导轨的时刻，只激活距接收线圈最近的发射导轨，以减少运行损耗，该方法可为抗横向偏移提供参考；文献[19]提出应用于导轨无线输电的电动汽车动态无线输电的偏移检测技术，通过测量3个排列成等腰三角形的形状、大小、电感值均相同的检测线圈的感应电压，来判断电动汽车偏移的角度和方向。

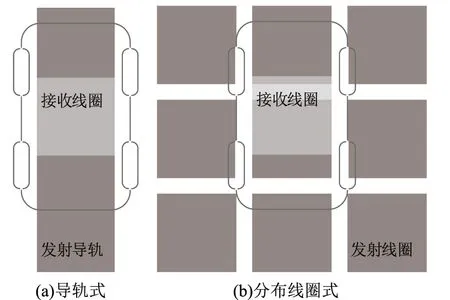
图1 道路无线输电系统Fig.1 Road wireless transmission system

分布式发射线圈在运行时仅有1个或几个线圈接通电源，与电流导轨相比，减少了损耗和磁链泄漏，电磁干扰更小[20]，且当电动汽车横向偏移程度大时，能切换至与接收线圈距离最近的发射线圈，系统运行更加灵活。基于此，本文提出应用于分布式发射线圈系统的接收线圈位置检测方法，通过检测接收侧4个感应线圈上的感应电压，计算接收线圈相对于发射线圈的偏移位置；通过仿真来设计计算方法并验证其准确性，再通过实验验证该方法的可行性。

1 理论分析

1.1 磁场分析

为了确定感应线圈的位置，首先分析发射线圈和接收线圈上电流产生的磁场的空间分布。根据毕奥萨伐尔定律[21]，通电长直导线上的电流元Idl在导线外的P点处产生的磁场

(1)

式中：I为流经长直导线的源电流；dl为源电流的微小线元素；μ0为真空磁导率，其值为4π×10-7T·m/A；D为电流元到P点间的距离；θ为电流方向和电流元到P点的连线的夹角；B为磁感应强度，dB为电流元在P点产生的磁感应强度。

因此，长度为L的导线在P点产生的磁场

(2)

本文假定发射线圈和接收线圈均为平面方形线圈且边长相同，它们产生的磁场可看成是4组长直导线的合成磁场，磁场的方向由右手定则确定；因此，合成磁场关于线圈纵横方向的中轴线都是对称的，如图2所示。

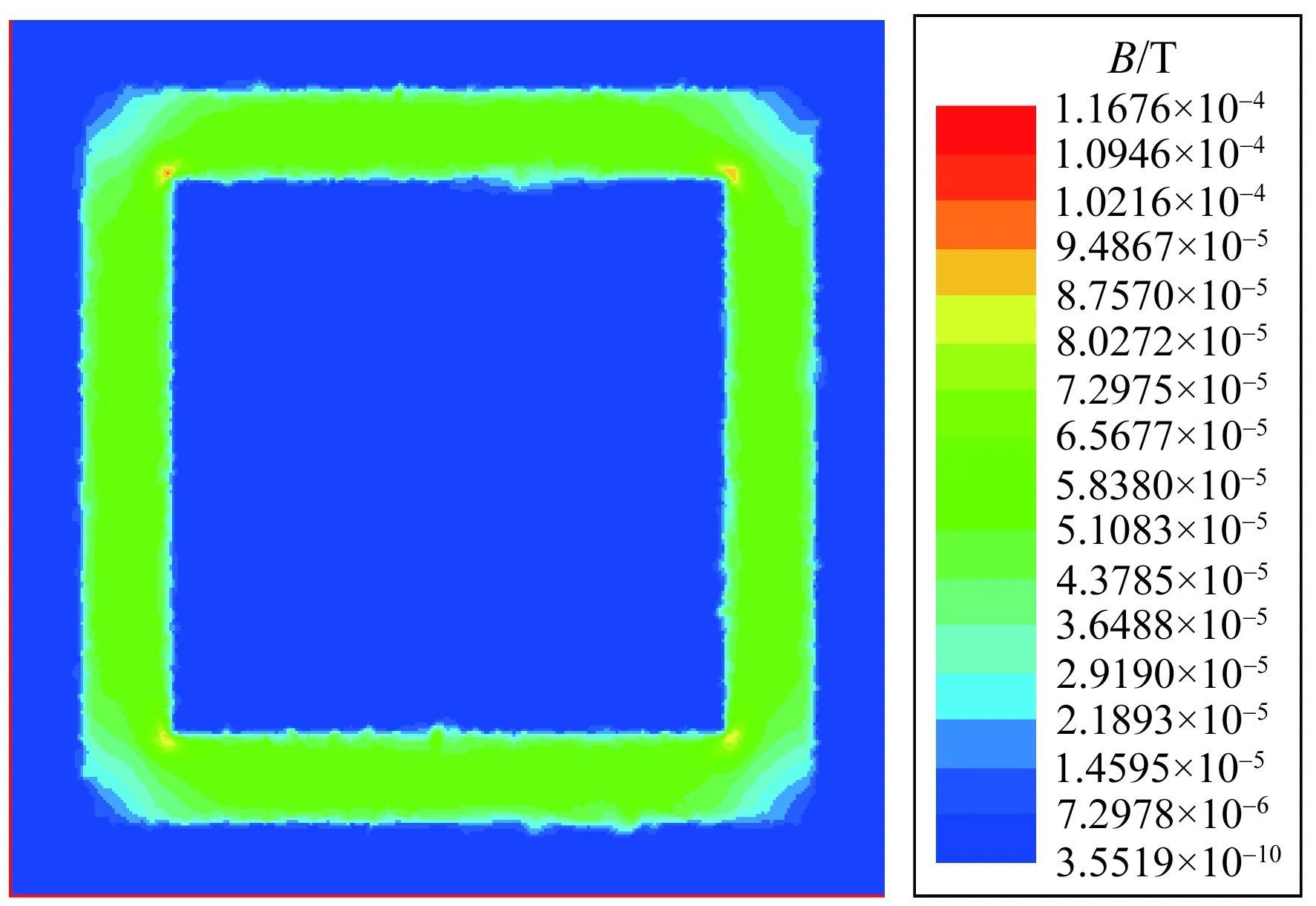
图2 方形线圈的磁场分布Fig.2 Magnetic field distribution of square coil

1.2 感应线圈设计

为了检测接收线圈相对于发射线圈的纵向和横向偏移，在接收线圈四边的上方分别设置感应线圈A、B、C、D，每个线圈的位置在每条线圈边的中间，且外侧与线圈边的外侧重合，如图3所示，其中h为感应线圈边长，b为接收线圈边长。

图3 感应线圈位置分布Fig.3 Positions distribution of induction coils

由于感应线圈所处位置具有几何对称性，电流在4个感应线圈内产生的磁场变化规律是相似的，因此只需分析其中1个感应线圈内的磁场。假设发射线圈和接收线圈的电流方向是逆时针，将两线圈基于中轴线分为左、右2个部分，其在感应线圈A的轴向产生的磁通分别为BA1l、BA1r和BA2l、BA2r，其中：下标第3位字母l和r分别表示发射或接收线圈左边部分和右边产生磁通；下标第2位数字“1”表示发射线圈，“2”表示接收线圈。流经发射线圈的电流为i1，流经接收线圈的电流为i2。当接收线圈位于发射线圈的正上方时，根据毕奥萨伐尔定律和右手定则，由于发射线圈和接收线圈的左、右2个部分与线圈A的距离相等，而电流方向相反，BA1l与BA1r、BA2l与BA2r大小相等，方向相反，可相互抵消，如图4(a)所示；因此两线圈在线圈A的轴向产生的合成磁通BA1和BA2都接近0，此时线圈A的感应电压接近于0。当发射线圈关于接收线圈发生横向偏移时，由于线圈A相对于接收线圈的位置没有变化，BA2l与BA2r的大小仍相等，因此BA2仍接近0；但是BA1l与BA1r不相等，如图4(b)所示，因此BA1不为0，线圈A的感应电压不为0，且不同的偏移方向和距离产生的感应电压方向和值不同。

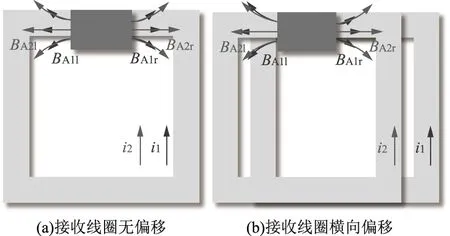
图4 线圈A的磁场Fig.4 Magnetic field of coil A

由于发射侧是分布线圈而非长直导轨，当接收线圈向前移动不同的距离时，即使横向偏移距离相等，线圈A的感应电压也不同；因此只设置线圈A时无法准确判断接收线圈相对于发射线圈的横向偏移距离，需要增设线圈B、C和D。线圈B、C和D的感应电压分析方法与A相似，但由于4个线圈位置不同，当接收线圈相对于发射线圈发生偏移时，4个线圈的感应电压关于偏移方向和距离的变化趋势不同。接收线圈分别向左和向右偏移时，线圈A和B上的感应电压变化趋势对称，而线圈C和D上的感应电压变化趋势不对称；接收线圈向前和向后偏移时，线圈C和D上的感应电压变化趋势对称，而线圈A和B上的感应电压变化趋势不对称。结合4个线圈检测到的感应电压，可以判断接收线圈的偏移方向并计算距离。

1.3 补偿拓扑分析

无线输电系统采用的基本补偿拓扑有SS(串联-串联)型、SP(串联-并联)型、PS(并联-串联)型、PP(并联-并联)型[22]以及T型，其中常用的T型拓扑包括LCL(电感-电容-电感)型和LCC(电感-电容-电容)型。SS、SP、PS和PP拓扑结构简单，补偿元件数量少，但是发射线圈的电流会随着互感和负载的变化而变化。而将LCL或LCC拓扑应用在发射侧，可以令发射线圈的电流不随着接收侧的参数变化发生剧烈变化[23-24]，这对于接收侧拾取电能以及感应线圈检测接收线圈的位置都是有利的。考虑到在电源电压相同的情况下，应用LCC拓扑可以比LCL拓扑获得更大的原边电流，因此在本文提出的系统中，采用LCC拓扑作为发射侧的补偿拓扑，接收侧则采用S(串联)型拓扑，以尽量减小接收侧电路的体积和重量。

电路拓扑如图5所示。其中：UDC为直流电压源，S1—S4为4个MOSFET，它们共同组成全桥逆变电路，L1为发射线圈自感，R1为发射线圈内阻，Ls1、C1和Cs1分别为LCC拓扑中的补偿电感和2个补偿电容，L2为接收线圈自感，R2为接收线圈内阻，C2为接收侧的补偿电容，RL为负载等效的交流电阻，us为发射侧输入的交流电压，is为发射侧的输入电流，u2为接收线圈的电压，M12为两线圈之间的互感。

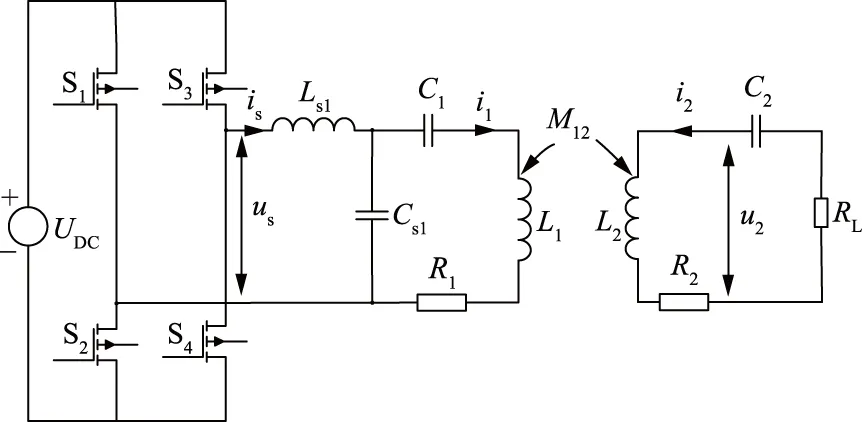
图5 系统电路Fig.5 System circuit

各补偿元件的参数由式(3)计算：

(3)

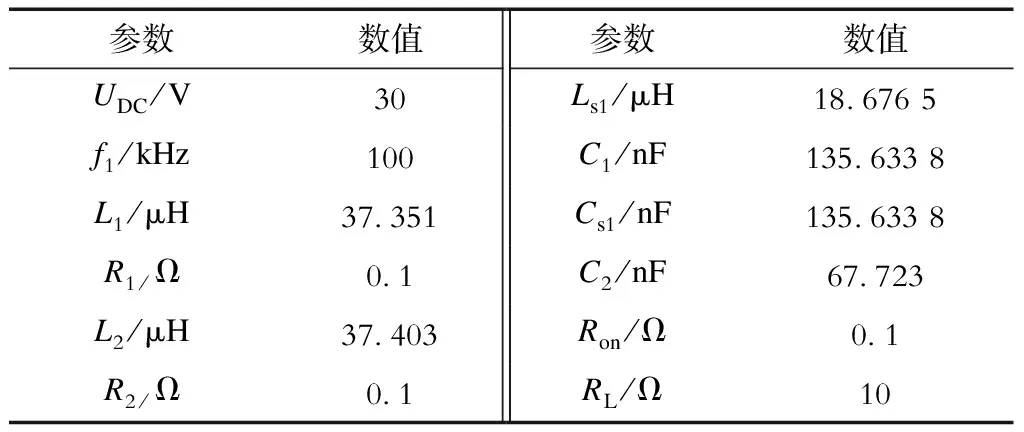
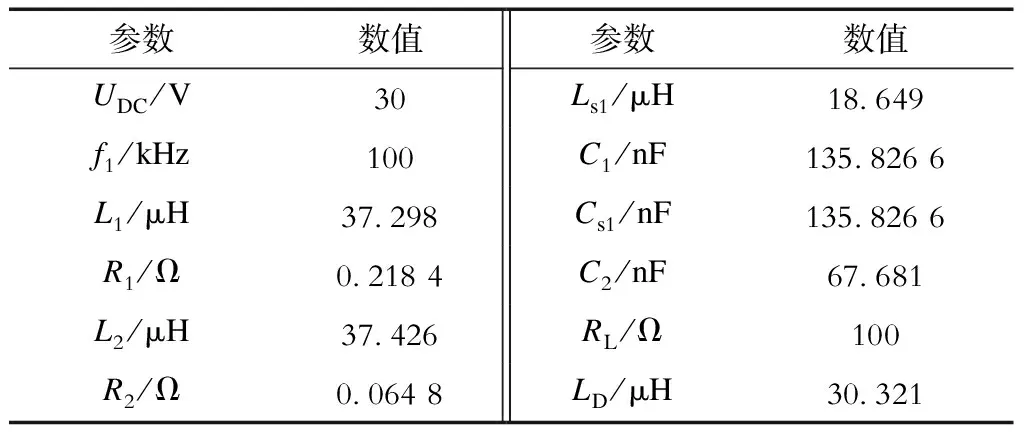
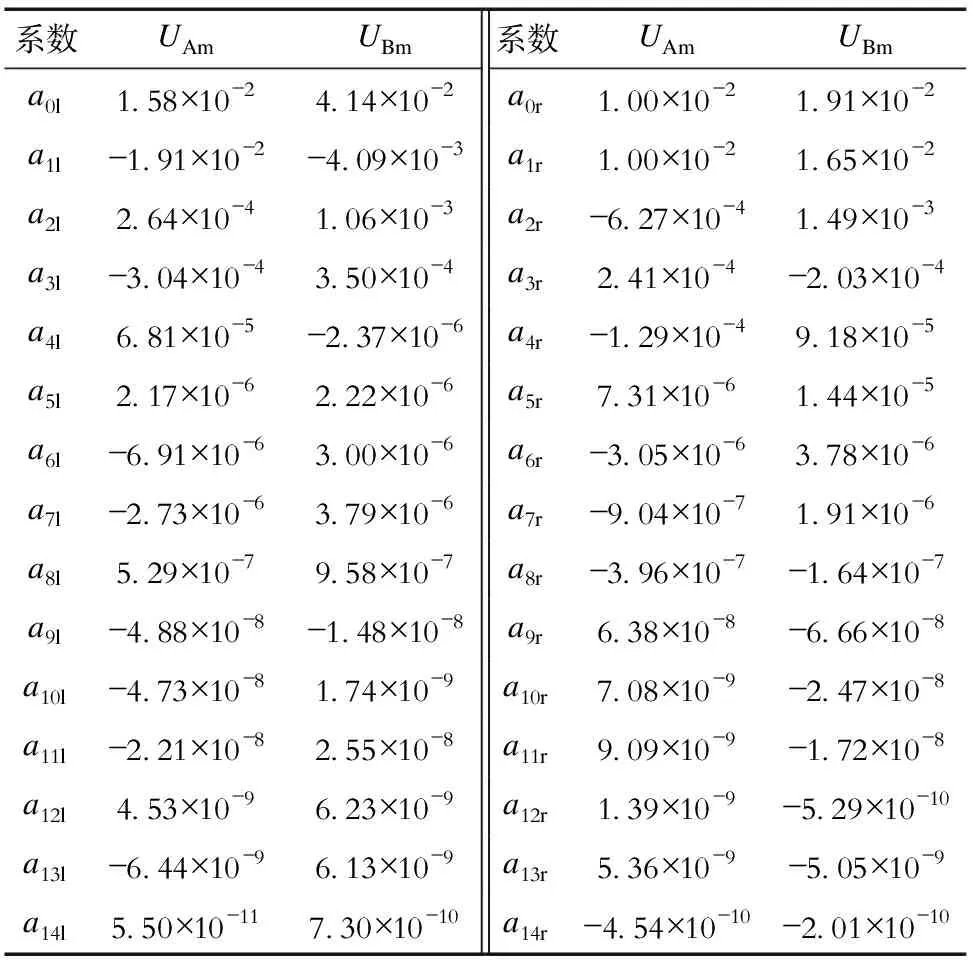
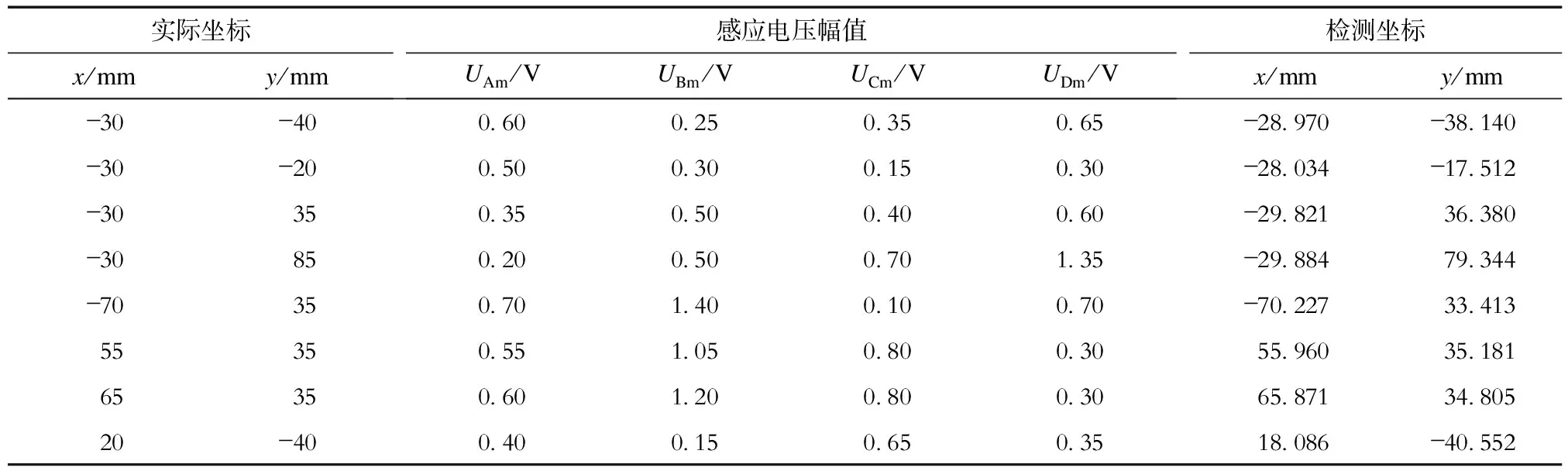
式中：ω1为谐振角频率；a为LCC拓扑的补偿参数，取值范围为0

虽然LCC拓扑的输入电流包含大量的高次谐波(除基波外)，但是经过该拓扑后，到达发射线圈的电流谐波含量已经很小，可以用基波近似法(FHA)来分析电路各部分的电流。假设电路的开关频率为f1，则接收侧的回路方程为

(4)

(5)

则接收侧反映到发射侧的阻抗

(6)

发射侧的输入阻抗

(7)

考虑MOSFET的导通电阻，发射侧的总阻抗

(8)

其中Ron为MOSFET的导通电阻。

直流电源经过逆变器输入到发射侧的电压为方波，经过傅里叶分解，可得其基波幅值

(9)

因此，发射侧的输入电流幅值

(10)

发射线圈上的电流幅值

(11)

接收线圈上的电流幅值

(12)

1.4 感应电压计算

不同电动汽车的接收线圈是不重合的，而且它们之间的距离较远，4个感应线圈装设在接收线圈上方，因此其他电动汽车的接收线圈与本汽车感应线圈之间的磁耦合相对于发射线圈与感应线圈之间的耦合很小，本文不考虑多接收线圈间的交叉耦合对检测性能的影响。设M1A、M1B、M1C和M1D分别为发射线圈与线圈A、B、C和D之间的互感，M2A、M2B、M2C和M2D分别为接收线圈与线圈A、B、C和D之间的互感，则线圈A、B、C和D上的感应电压相量

(13)

式中下标p∈{A，B，C，D}，表示这4个线圈之一。

感应电压的幅值

(14)

由于4个感应线圈都固定在接收线圈的中轴线上，接收线圈产生的磁场在每个感应线圈内都可抵消，因此接收线圈和感应线圈之间的互感很小，从而接收线圈的电流对感应线圈的感应电压影响很小。感应电压主要反映发射线圈和感应线圈之间的互感，即反映两者的相对位置。

2 有限元仿真分析

2.1 Maxwell仿真分析

由上述分析可知，在电路各参数都确定的情况下，感应线圈的感应电压由发射线圈和接收线圈之间的互感M12、发射线圈和感应线圈之间的互感M1p以及接收线圈和感应线圈之间的互感M2p决定。为了获得感应线圈的感应电压与接收线圈相对于发射线圈的偏移位置的关系，本文通过Maxwell仿真来获取不同偏移位置下的M12、M1p和M2p，再通过计算得到4个感应线圈的感应电压幅值Upm。

仿真中，设定的线圈参数为：发射线圈、接收线圈和感应线圈的线径为2.34 mm；发射线圈和接收线圈的外边长均为200 mm，匝数为10，内边长均为176.6 mm；感应线圈的边长30 mm、20 mm，匝数为21，线圈高50 mm；传输距离为50 mm。4个感应线圈分别位于接收线圈的4个线圈边的上方中间，且其外侧与接收线圈边的外侧重合。当偏移距离过大时，电源通常切换至距离接收线圈最近的发射线圈，因此在偏移距离太大时,主动调节发射线圈的位置使之接近前一个发射线圈已无意义。本文仿真和实验设定最大的纵向和横向偏移距离均为发射线圈边长的一半，即100 mm。用x来表示横向偏移，y表示纵向偏移，x<0表示向左偏移，x>0表示向右偏移，y<0表示向后偏移，y>0表示向前偏移，则x和y的取值范围均为-100～100 mm。设置计算感应电压的电路具体参数见表1。

表1 仿真电路参数Tab.1 Simulational circuit parameters

由式(3)可知，随着a增大，Cs1增大，而C1减小，为了使C1和Cs1都不至于过大，仿真和实验中均取补偿系数a=0.5。接收线圈在相对于发射线圈的不同位置时，感应线圈A、B、C、D的感应电压幅值的变化趋势如图6(a)—(d)所示。

图6 感应线圈电压幅值Fig.6 Voltage amplitudes of induction coil

由图6可知，UAm和UBm各自关于x轴对称，UCm和UDm各自关于y轴对称，且4个线圈的感应电压的关系可以表示为

UAm(x,y)=UBm(x,-y)=

UCm(-y,x)=UDm(y,x).

(15)

由于仿真时相邻测量点之间的距离是25 mm，通过仿真只能计算数量较少的点的感应电压，而从图6可以看出感应电压幅值随着接收线圈偏移位置的变化是连续变化的；因此可以采用拟合的方式，求测量点以外的点的感应电压。为了得到感应电压幅值随线圈位置变化的表达式，采用二元多项式进行拟合。由于UAm和UBm各自关于x轴对称，UCm和UDm各自关于y轴对称，可以将它们分别以x轴和y轴为界分成两半拟合，以减少拟合次数。通过拟合对比，发现4次多项式拟合得到的点的误差平方和已达到0.001 355，因此，本文采用二元四次多项式拟合对感应电压幅值散点进行三维拟合，得到的UAm、UBm、UCm和UDm如图7所示。

图7 感应线圈电压幅值拟合Fig.7 Fittings of induction coil voltage amplitudes

由图7可以看出，经过拟合后，可以更精确地确定接收线圈在每个偏移位置时4个感应线圈上的感应电压幅值。感应电压幅值可表示为

Upm(x,y)=a0s+a1sx+a2sy+a3sx2+

a4sxy+a5sy2+a6sx3+a7sx2y+

a8sxy2+a9sy3+a10sx4+a11sx3y+

a12sx2y2+a13sxy3+a14sy4.

(16)

式中：下标s∈{f，b，r，l}，表示线圈坐标所处象限f、b、r、l之一；当x<0时，UAm和UBm的系数形式为ail；当x>0时，UAm和UBm的系数形式为air；当y<0时，UCm和UDm的系数形式为aib；当y>0时，UCm和UDm的系数形式为aif。ais(i=0，1，…，14)为四次多项式的各项系数，可通过解法方程组(17)得到。

(17)

其中，基函数φi可由式(18)表示，di和(φi,φj)(j=0，1，…，14)可分别由式(19)和式(20)计算得出，其中(xu,yv)为第u、v个采样点的偏移位置。

(18)

(19)

(20)

2.2 判断偏移位置的方法

经过多项式拟合，得到4个分段电压函数表达式，可以通过解方程组，求当前接收线圈的位置。解非线性方程组一般采用迭代法，本文采用牛顿迭代法来求解。牛顿迭代法虽然收敛速度较快，但是初值的选取会影响求解结果，初值选取不当甚至可能导致解不收敛。求解2个未知数x和y只需2条方程，因此可以联立其中2条方程，用牛顿迭代法得到符合要求的解，再用余下的2条方程检验，若该解不符合另外2条方程的要求，则另选初值，再次迭代，直到得出同时符合4条方程的解。由式(15)可知，若接收线圈的偏移位置为(x1,y1)，感应线圈A、B、C、D的感应电压幅值分别等于UAm(x1,y1)、UAm(x1,-y1)、UAm(-y1,x1)、UAm(y1,x1)；因为线圈A和D、线圈B和C的电压幅值既不关于x轴对称，也不关于y轴对称，可选择线圈B和C的电压方程来求解x和y，用线圈A和D的电压方程来检验求解结果。图8所示为求解的完整流程。

求解的主要步骤如下：

步骤1，检测横向和纵向偏移-100～100 mm范围内每相隔25 mm、共81个点的4个感应电压幅值，对这些散点进行二元四次多项式拟合，通过解法方程组求得各拟合系数，得到4个感应电压幅值表达式。

步骤2，检测在当前点的4个感应电压幅值uAm、uBm、uCm和uDm，判断位置坐标所在的象限，选择正确的电压幅值表达式，并在所在象限内选择迭代初值x0和y0。

步骤3，用牛顿迭代法求解方程组

(21)

得到符合精度要求的x和y。

步骤4，判断x和y的值是否在-100～100 mm之间，并检验x和y是否满足

(22)

式中ε为检验精度。

步骤5，如果取值和精度都满足要求，则停止计算，获得当前点的位置坐标，否则转步骤6。

步骤6，在所在象限内选取另一组迭代初值x′0和y′0，转步骤3。

2.3 仿真验证

为了验证上述方法能否准确地计算位置坐标，选取一些点，通过仿真得到感应线圈的感应电压幅值，计算得到的坐标和实际坐标见表2。

表2 仿真实际坐标和计算坐标对比Tab.2 Comparisons of actual and calculated coordinates in simulation

由表2可知，该方法在大多数情况下能较准确地计算位置坐标，当偏移距离增大到一定程度时，如点(-30,85)，计算误差增大；这是由于方程组是通过多项式拟合得到的，方程组确定的曲面上的点与实际点存在误差。

图8 求解流程Fig.8 Solution flow chart

3 实验验证

基于理论分析和仿真设计，本章通过实验来验证上述方法的可行性。主要实验装置如图9所示，其中：直流输入电压UDC=30 V，4个MOSFET管IRFP260N组成全桥逆变器，数字信号处理器TMS320F28335PGFA提供4路100 kHz、占空比为50%的脉冲宽度调制(pulse width modulation，PWM)信号，经过悬浮驱动器IR2110分别驱动4个MOSFET管，发射线圈、接收线圈的线圈参数与仿真相同；为了简化实验，只绕制1个感应线圈，令其在不同的位置分别充当4个感应线圈，感应线圈的线径为1 mm，边长为40 mm、30 mm，高为40 mm，匝数为33，电感值为LD。系统的传输距离为50 mm，电路参数见表3。

图9 主要实验装置Fig.9 The main experimental device

表3 实验电路参数Tab.3 Experimental circuit parameters

在各检测点时4个感应电压幅值如图10所示。由于实际绕制的线圈不是理想线圈，因此实验结果与仿真有差异，但是感应电压幅值变化的总体趋势相同。

图10 实验感应电压幅值Fig.10 Experimental voltage amplitudes of induction coil

由实验数据计算得到的4个接收线圈的感应电压幅值表达式系数见表4、表5。

表4 感应电压UAm、UBm幅值表达式系数Tab.4 Coefficients of induction voltage amplitude expressions of UAm、UBm

表5 感应电压UCm、UDm幅值表达式系数Tab.5 Coefficients of induction voltage amplitude expressions of UCm、UDm

为了验证位置检测方法的可行性，选取几个点检测4个感应电压的幅值大小，采用本文所提的方法获得的位置坐标和实际位置坐标对比见表6。

由表6可知，无论横向偏移相同、纵向偏移不同时，还是横向偏移不同、纵向偏移相同时，检测得到的位置坐标和实际位置坐标较接近，可以证明该检测方法是可行的。

表6 实际坐标和计算坐标对比Tab.6 Comparisons of actual and calculated coordinates

4 结束语

本文针对动态无线电能传输系统中接收线圈相对于发射线圈偏移引起的互感下降问题，提出基于4个感应线圈的位置检测方法，对在4个感应线圈上检测到的感应电压进行拟合，求它们的感应电压幅值表达式，再运用牛顿迭代法，求解接收线圈的位置坐标。本文所做的主要工作有：①通过理论分析，确定所需感应线圈的数量和安装位置，以及适用于系统的发射侧补偿拓扑；②通过仿真，设计了求解的具体实现步骤并验证该方法的准确性；③通过实验，验证方法的可行性。

本文所提检测方法可以在接收线圈位于相对发射线圈不同的纵向位置的情况下，检测接收线圈的横向偏移，以保证发射和接收线圈之间的互感尽可能保持最大。该方法无需经过复杂的计算，且只需要4个感应线圈，安装成本较低，可为分布式发射线圈动态无线输电系统中接收线圈的位置检测提供参考。但是该方法需要预先测量4个感应线圈在多个点的电压幅值，这要求电动汽车在投入使用之前必须先通过试验确定4个电压方程，而且对于发射线圈参数不同的试验场景，电压方程也不同，增加了试验的复杂度，这是该方法投入应用的主要局限性。