基于轨迹相似度的行人轨迹预测方法研究

王爱兵， 刘亚朋， 夏 辉， 罗 磊

(1.河北交通职业技术学院 汽车工程系，河北 石家庄 050035；2.河北劳动关系职业学院 信息科学与工程系，河北 石家庄 050002)

行人的运动轨迹数据对于交通安全、智能机器人导航等领域具有十分重要的价值和意义.要对行人的运动轨迹进行研究，应采集行人的各项数据并对数据进行离线分析，在充分了解行人的行为及周围环境的具体情况后，再给出合理的决策分析结果[1].而根据行人在过去时刻的具体运动轨迹，预测出未来时刻的运动轨迹是存在一定困难的[2]，这是由于行人在运动过程中具有一定的随机性，因此在相应的预测任务中生成一条精确的轨迹是不可能的.每个行人并不是单独存在的个体，文献[3]表明，七成以上的行人更倾向于成群行走或在同一个空间下交互行走.而这些均会增加行人轨迹预测的难度.

轨迹相似度是在轨迹模式匹配的过程中，结合轨迹对应位置的匹配原则，来计算当前轨迹与历史轨迹的相似程度，再根据相似度的阈值判定来得出轨迹预测结果的[4].轨迹相似度的应用十分广泛，如语音识别分类、模板匹配、信息检索等方面.在实际应用中，通过轨迹相似度可以更加准确地预测出移动目标的未来运动轨迹.因此，将轨迹相似度引入行人轨迹预测中，可以增加预测结果的准确度.

1 社会关系影响下的行人轨迹建模

将对行人轨迹的预测问题归类为对序列的决策问题.一个独立的行人a在某一时刻t时，不仅与当前位置的信息和过去的状态相关，同时也与周围其他行人对其的影响相关[5].因此，为了准确地分析其他行人对被预测行人的影响，结合行人之间的社会关系对被预测行人的影响，对被预测行人轨迹进行建模.假设行人相互之间的社交关系为Pij，其表达式为：

(1)

在得到行人之间的社交关系表达式后，可进一步得到两名行人在行进过程中的夹角ωij，表达式为：

(2)

公式(2)中，ωij表示其他行人j与被预测行人i之间的方位夹角.

据公式(1)可得两名行人之间的最短距离：

(3)

公式(3)中，Cij表示两名行人的最短距离，也可表示两名行人在行进过程中将要达到的最小夹角.两名行人间的方位夹角能反映被预测行人的运动状态的方向信息.相对距离的大小会直接影响行人之间的交互情况.相对距离越小，行人之间的交互影响力越大；相对距离越大，行人之间的交互影响力越小.

通过对最短距离的计算，可提取到更加有效的防碰撞特征数据.利用人类视觉注意力机制，可从行人行进过程众多的信息中获得最有效、最关键的信息[6].当被检测行人与周围行人交互较为复杂时，行人会结合当前自身的行进状态及周围行人对自己的影响，快速作出相应的行进决策，并改变原始的行进轨迹[7].为得到周围行人对被预测行人的影响情况，采用编码器输入隐藏量；同时结合被预测行人与行人交互后得到的特征数据，可得到行人在行进过程中的注意力数据.通过添加人类视觉注意力机制，使行人轨迹模型不仅可以处理复杂场景下的行人交互问题，而且可以为后续的轨迹预测计算增加可解释性，并抑制部分冗余数据，从而将更多的重点放在对行人行进轨迹重要特征的提取中，从而缩短收敛时间，节省计算资源.

2 基于轨迹相似度的行人轨迹相似度计算

为方便后续描述，本文以图1为基础，来计算行人的轨迹相似度.

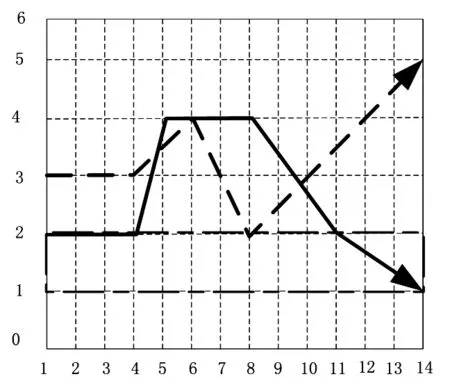
图1 行人历史轨迹选取示意图

图1中，实线部分表示被预测行人的行进轨迹，虚线部分表示其他行人的行进轨迹，矩形方块表示该行人行进轨迹的横纵坐标范围.在寻找该名行人历史轨迹相对应的路线时，首先，通过遍历图1中虚线部分的每一个点，找到第一个同时满足横纵坐标均在其范围内的轨迹点[8].其次，继续遍历后续其他行人的轨迹点，并将得到的所有轨迹点引入到子轨迹点集合中，直到找不出横纵坐标均在规定范围内的轨迹点时，停止遍历操作.这样保留下来的连续子轨迹即为当前行进轨迹对应的行进预测轨迹.由于存在多条周围其他行人的轨迹与被预测行人轨迹类似，并且轨迹段相似度差异较小[9]的情况，因此，需要对被预测行人的轨迹进行二次分析.若出现多条其他行人轨迹时，根据当前轨迹的相似度，可得出更加符合被预测行人轨迹的走向，并根据算法流程进行轨迹的相似度计算.

第一步，读取被预测行人的当前轨迹和历史轨迹数据.

第二步，对当前行人的轨迹和历史轨迹进行预处理.

第三步，对当前被预测行人的轨迹、历史轨迹数据与周围其他行人的行进轨迹相对比，计算得出两者的相似度，组成轨迹点集合.

第四步，分别计算相似度.相似度的计算公式为：

(4)

公式(4)中，λ(Q,L)表示轨迹段的相似度；k表示轨迹段的阶数；d(Qi,Lij)表示当前轨迹点集合与历史轨迹点集合中第i个对应轨迹点的欧式距离.

第五步，选择相似度值最小的前15%的轨迹数据作为最终轨迹进行偏差计算.

第六步，找出最相似的轨迹数据并输出，完成对被预测行人轨迹的计算.

3 行人轨迹预测点简化

为快速得到预测出的行人轨迹，对轨迹点进行简化处理，需要完成两次简化.

3.1 第一次简化过程

将所有预测得出的轨迹点组成一组轨迹.从第二个轨迹点开始，分别计算前一个轨迹点与后个一轨迹点间的斜率[10].由于在现实情况下，行人行进轨迹的首位横坐标相同时会造成斜率溢出现象[11]，因此，选择将首位轨迹点横坐标之差设定在(0.001，+∞)范围内.若斜率差较大，说明被预测行人在这一点上的方向变化较大，应当保留该点；若斜率差较小，说明被预测行人在这一点的方向变化不大，可将该点删除.

3.2 第二次简化过程

(1)对行人历史轨迹进行初始化处理，并将个体定义为完成一次精简后的轨迹点，轨迹上个体的数量是经过精简处理后轨迹点的3倍.(2)利用多点变异法计算轨迹点的变异率，并根据需要对一次精简后的轨迹点进行取舍.(3)采用分段杂交方法选择个体，且选择数据较小者.(4)保持适应度稳定不变，5轮迭代后停止.(5)将得出的轨迹点依次按顺序连接，即可得到行人轨迹的预测结果.

4 实验与结果分析

4.1 实验条件

由于要对行人行进过程中的轨迹进行预测，因此选用移动目标的行进轨迹数据集作为实验数据集.实验过程中的主要参数见表1.

表1 实验过程中的主要参数

选用被预测行人的某条当前原始轨迹作为实验对象.为方便后续描述，假设该轨迹的编号为A，则简称其为A轨迹.分别利用本文所提方法与传统方法对行人的行进轨迹进行预测.为保证实验过程的公正性，设置轨迹处理的时间均为2 s一次；在选择抽样轨迹点时，每4 s抽取一个轨迹点；为传统方法和本人所提方法均采集5个样本.抽取的轨迹点情况见表2.

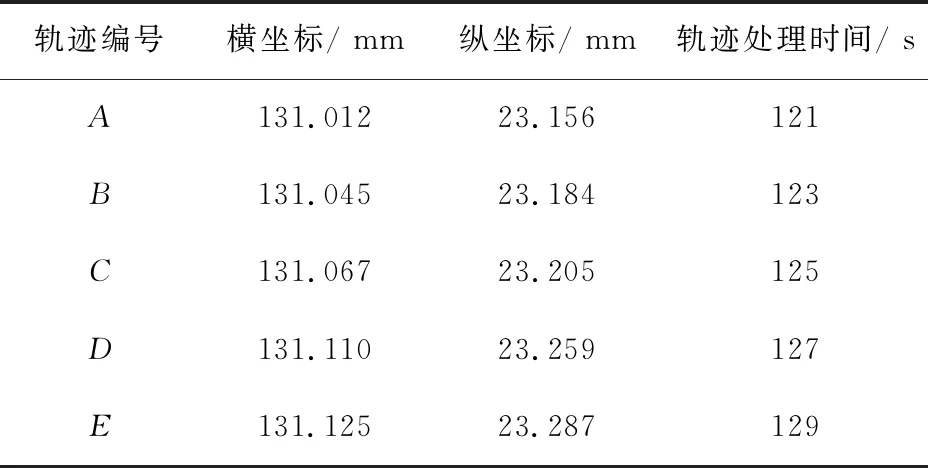
表2 抽样轨迹点数据

为验证两种轨迹预测方法的有效性，实验过程中将起始点位置记为原点.将两种预测方法的预测结果与5名行人下一时刻的实际行进轨迹进行对比，并按照公式(5)计算预测结果与实际行进结果的偏差量R.

(5)

公式(5)中，R表示两种预测方法得出的轨迹预测结果与行人实际行进结果之间的偏差量；x表示水平方向上的位置差值；y表示竖直方向上的位置差值.

4.2 实验结果分析

按照公式(5)，计算两种方法的预测结果与实际5名行人的行进轨迹偏差值，得到表3.

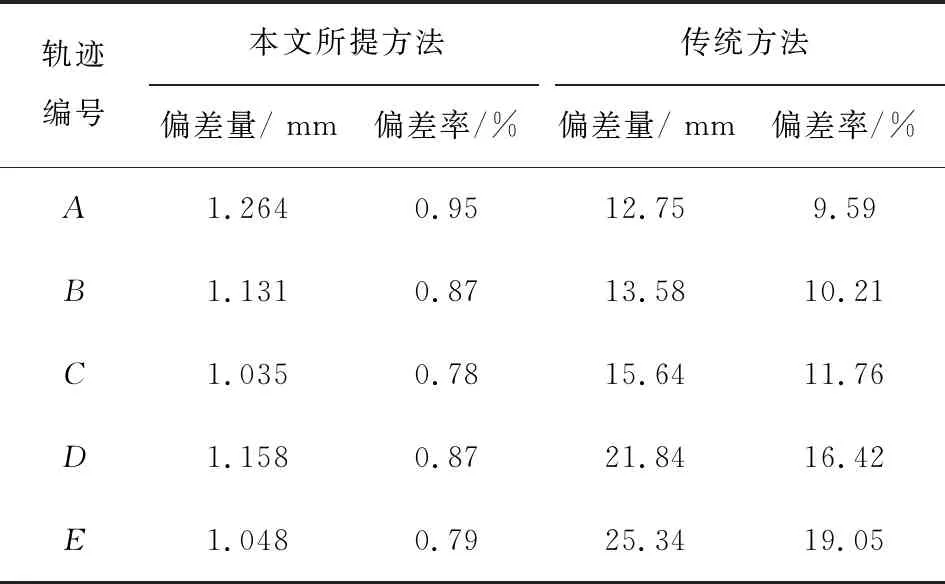
表3 实验结果对比表

由表3可知，在对随机性较大，易受周围因素影响的行人行进轨迹进行预测时，本文设计的基于轨迹相似度的行人轨迹预测方法的偏差量明显小于传统方法，且偏差率比传统方法小10倍左右.传统轨迹预测结果产生较大差异的主要原因是，在实验过程中，无法对行人的各类不确定性因素进行判断，也未考虑到被预测行人会受到周围其他行人的影响.而本文所提方法在预测过程中，采用了轨迹相似度的方法，将被预测行人的历史轨迹与周围其他行人的轨迹进行了对比，这就有效地保证了预测结果的准确性和真实性.

5 结语

通过实验证明了基于轨迹相似度的行人轨迹预测方法的可行性.将此方法应用到交通安全领域、告警系统中，可以得到更高的预测准确度.在后续的研究中，将增加影响行人行进轨迹的因素，设计出更具综合性和全面性的预测方法，以进一步提高预测结果的精确度.