冰流撞击作用下高速铁路桥梁振动抑制研究
2021-04-28李鹏浩和振兴石广田
李鹏浩,和振兴,石广田
(兰州交通大学 机电工程学院,兰州 730070)
近年来,随着我国高速铁路运营里程的不断增大,运行速度的不断提高,铁路桥梁安全问题日益严峻.桥梁在交付使用过程中除了受到列车和桥梁之间的相互振动外,还会受到来自外部荷载的影响,如地震[1-3]、泥石流[4]、落岩[5]、风荷载[6]和撞击[7-8]等.在我国北纬35°以北地区,尤其是东北地区、青藏高原和川藏铁路沿线地区的桥梁在春季冰融时节经常受到河流中流冰的撞击.在凌汛严峻的时节,流冰撞击会对桥墩造成不同程度的损伤.流冰撞击桥墩时,会使桥墩产生横向振动,严重时会造成主梁与支座的偏移,甚至造成落梁现象,严重威胁桥梁结构安全[9-10].目前关于研究流冰对桥梁撞击的文献较多[11-12],于天来[13]通过LS-DYNA就流冰对桥墩的撞击力进行了有限元仿真,并与实测冰击力进行对比,验证了有限元计算结果的准确性.
流冰撞击桥墩会使墩顶和主梁产生较大的位移和振动,对乘客的乘坐舒适性和列车的运行安全性可能造成影响.流冰撞击桥墩的荷载是一种偶发自然力,与之类似的有地震荷载和风荷载等.对于地震荷载和风荷载引起的桥梁振动可采用TMD进行抑制.
目前TMD减振技术多用于桥梁抗震、抗风等领域,而对于流冰撞击作用下TMD对桥梁的振动抑制未见研究.基于此,采用LS-DYNA建立流冰-桥墩有限元模型计算流冰撞击荷载,并建立考虑流冰撞击影响的铁路桥梁-TMD减振模型,初步探讨了TMD对冰击荷载作用下桥梁振动的抑制效果,为后续研究流冰撞击作用下列车-轨道-桥梁系统振动控制提供理论依据.
1 TMD系统撞击减振设计
1.1 随机激励下TMD设计理论
TMD减振系统设计需确定三个主要参数:质量比、刚度和阻尼.图1所示为随机激励作用下的TMD减振系统力学模型.其中,m1、k1、c1分别为主结构的质量、刚度和阻尼系数;m2、c2、k2分别为TMD的质量、刚度和阻尼系数;x1为主结构位移,x2为TMD位移,F(t)为外部随机荷载.
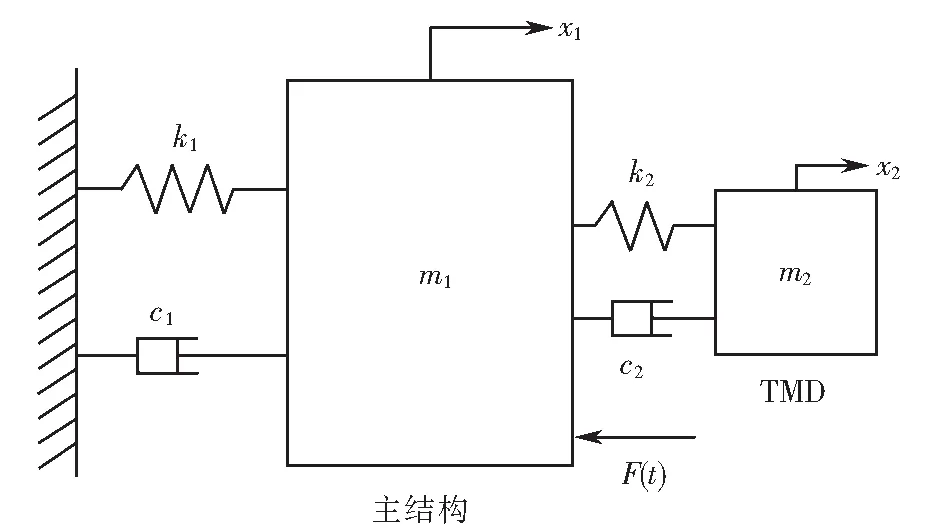
图1 随机激励作用下TMD-单自由度结构示意图Fig.1 Schematic diagram of TMD-single degree of freedom structure under random excitation
根据达朗贝尔原理,上述力学模型的运动方程如下所述
(1)
基于传递函数和拉普拉斯变换准则,主结构位移和随机激励之间的传递函数[16]可表示为
(2)

以主结构位移x1的方差为减振衡量标准,文献[16]详细推导了在白噪声随机激励下TMD的最优频率比fopt和ζopt阻尼比,可表示为
(3)
由公式(3)可得,随机激励作用下TMD系统的最优刚度和阻尼分别为
(4)
根据公式(4),可以计算随机激励下单自由度系统上TMD的最优刚度和最优阻尼.
降水中的稳定同位素D与18O在补给过程中,将大气D与18O的信号传递给地下水,地下水在渗透的过程中使得水中同位素的含量发生变化,这些变化为地下水来源调查提供了基础[15]。地下水的δD与δ18O含量在垂向上具有明显的分层特点,整体表现为随着地下水的埋藏深度的增加,地下水的δD与δ18O值逐渐偏负,指示着地下水不同含水层段上水力联系微弱[16]。
由于桥梁结构是一个连续弹性体系,上述计算单自由度系统TMD最优参数的方法不能直接用于桥梁结构中[17].参照文献[15],依据TMD安装位置和所控模态,通过动能理论计算结构等效质量和刚度.
(5)
式中,T为系统动能,Mij为桥梁第i阶模态j点处的等价质量,ωi为第i阶固有频率,{x1,…,xj,…,xN}为系统特征向量,{m1,…,mj,…,mN}为离散的单自由度质量,Kij为桥梁结构第i阶模态j点处的等价刚度.
依据公式(4)和(5)可以确定TMD的最优参数.
1.2 冰击荷载计算
流冰撞击桥墩是一个复杂的动态过程,撞击在很短的时间内产生巨大的撞击力和能量转换,涉及到非线性和大变形理论.
采用LS-DYNA软件建立了流冰-桥墩撞击有限元模型.桥梁为高速铁路32 m简支梁桥,梁高3.05 m,宽13.4 m,桥墩为重力式墩,墩长7.8 m,宽3 m,高25 m;冰排尺寸为40 m×20 m×0.6 m,桥梁结构截面尺寸如图2所示.建模中将主梁和二期恒载作为附加质量施加在桥墩上.由于重力式桥墩刚度较大,冰与桥墩撞击过程中冰排持续破碎,桥墩处于弹性状态,因此桥墩建模时采用线弹性模型.在传统的流冰撞击力计算模型中,由于冰排的应变速率较高,建模中可简化为线弹性材料模拟并设置冰的脆性破坏条件;参考河冰单轴压缩实验[18],以实验数据为依据,采用与应变速率相关的塑性材料模拟冰的特性,流冰破坏条件依据最大拉应力失效准则,这样既能模拟低应变速率下冰的屈服状态,又能模拟流冰高应变速率下的破碎现象.桥墩和冰排主要参数如表1所示.
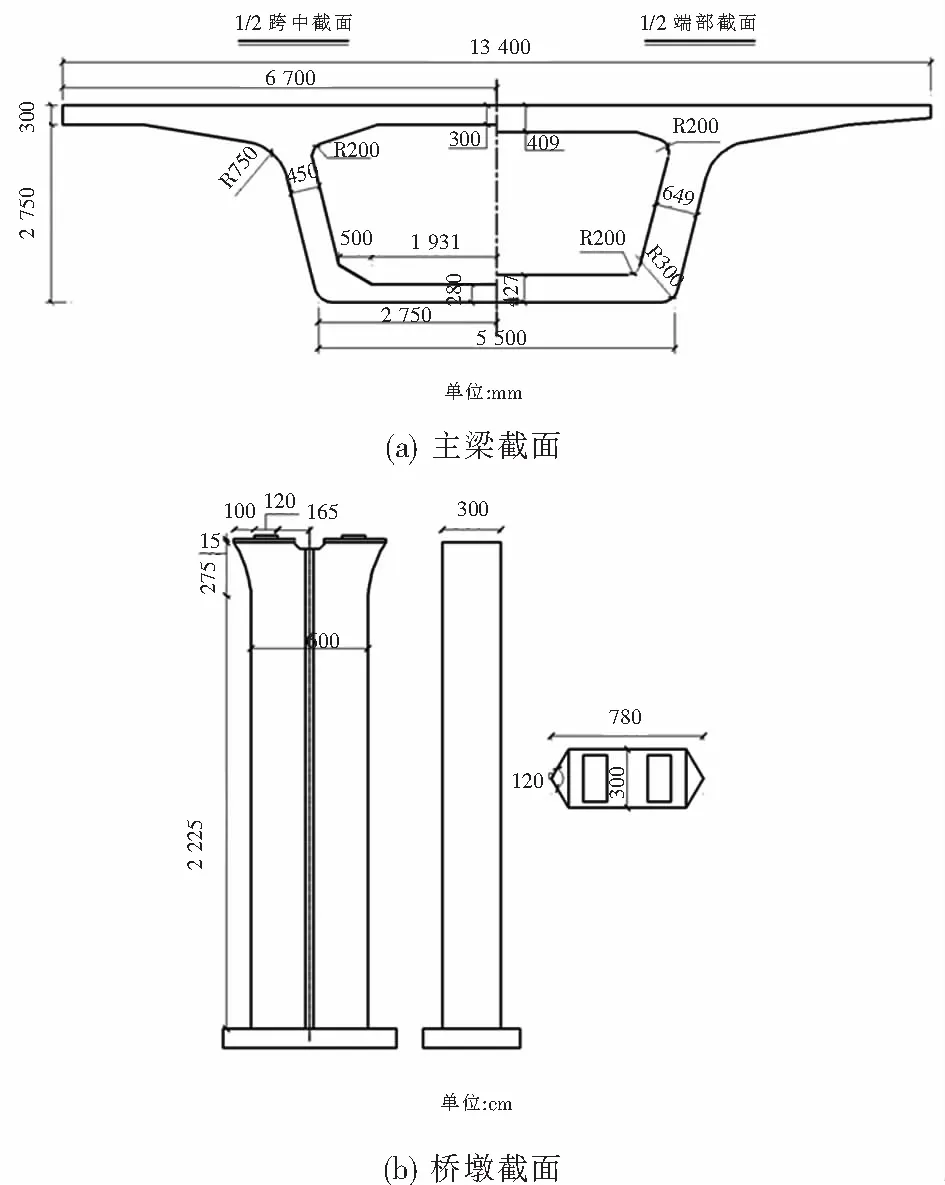
图2 主梁和桥墩横截面和尺寸Fig.2 Cross-section and main dimensions of bridge and pier
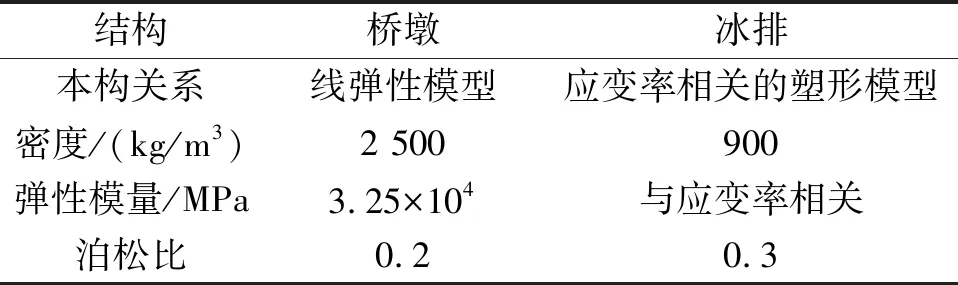
表1 桥墩和冰排主要参数
建模中冰排和桥墩均采用solid164单元模拟,桥墩单元尺寸为0.4 m×0.4 m×0.4 m.由于冰与桥墩接触部位的单元尺寸大小直接影响冰击力计算结果的精度[12],冰排中间部分单元大小为0.15 m×0.15 m×0.3 m,冰排两端单元尺寸大小为0.15 m×0.4 m×0.3 m,冰排撞击位置为距墩底5 m处.为了避免冰排与桥墩初始状态发生穿透现象,建模时使桥墩和冰排的初始距离为0.1 m,流冰-桥墩撞击有限元模型如图3所示.模型计算过程中,接触类型采用双向接触算法中的ASTS(面与面自动接触),接触算法采用对称罚函数算法.图4~图5为冰排抗压强度为2 MP时冰击力时程曲线和频谱曲线.

图3 流冰-桥墩撞击有限元模型Fig.3 Floating ice-pier collision model
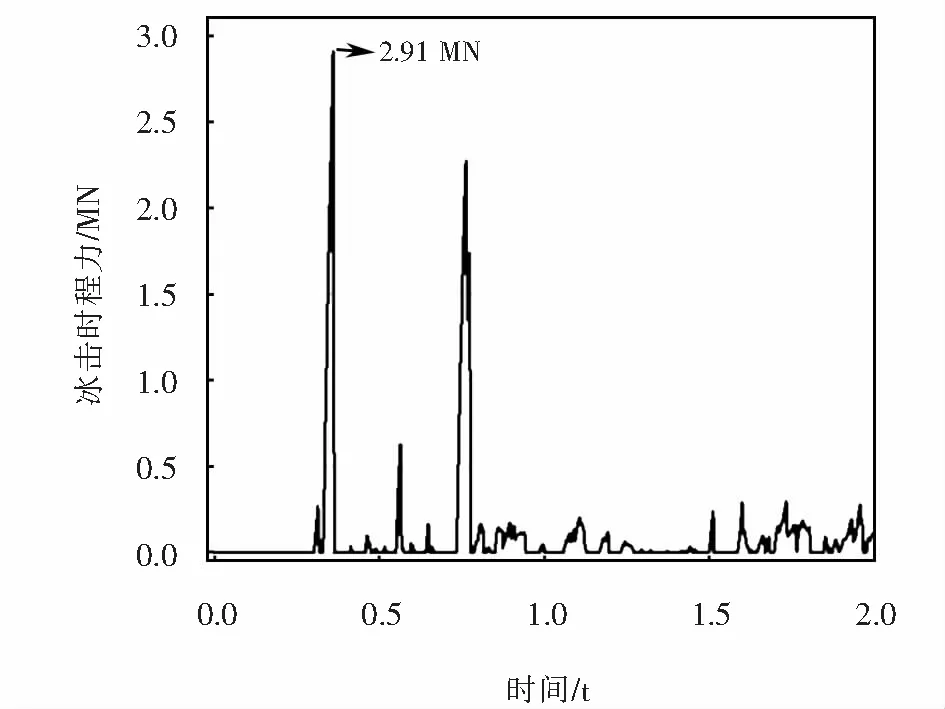
图4 冰击力时程曲线Fig.4 Time history curve of ice collision load
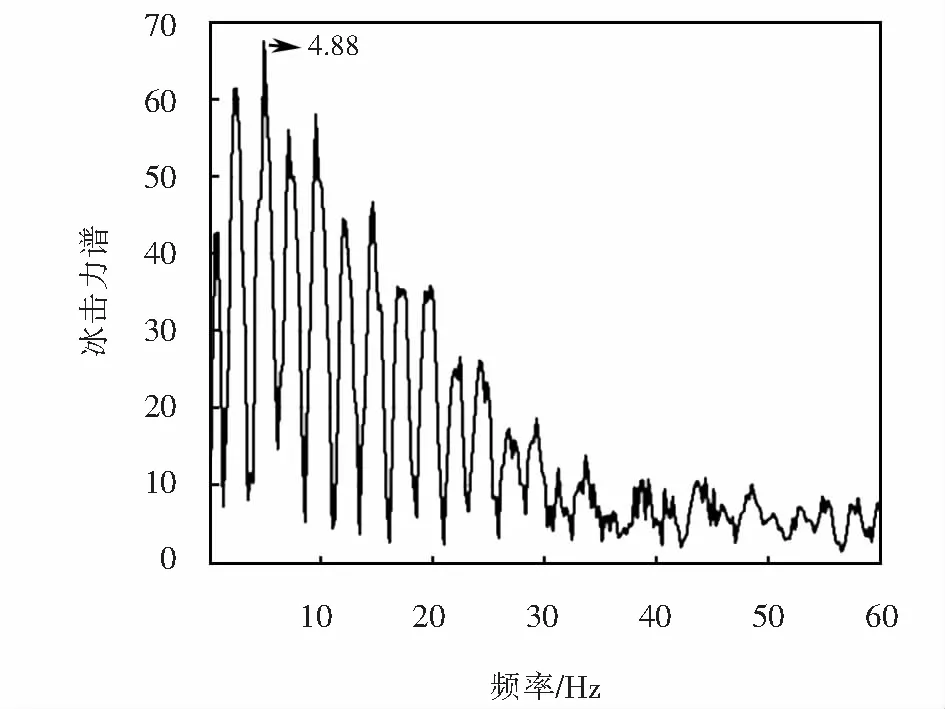
图5 冰击力频谱Fig.5 Frequency spectrum of ice collision load
《公路桥涵设计通用规范》中冰击力计算公式可表示为
Fi=mCtbtRik.
(6)
式中,Fi表示冰压力标准值(kN);m表示墩迎冰面形状系数;Ct表示冰温系数;b表示墩迎冰面投影宽度;t表示计算冰厚;Rik表示冰的抗压强度标准值.
由公式(6)计算的冰击荷载为2 772 kN,由流冰-桥墩有限元模型计算的峰值为2 910 kN,可见有限元模型计算结果峰值与《公路桥涵设计通用规范》计算结果基本吻合,二者误差仅为4.7%,并且有限元模型计算结果略大,说明采用有限元模型计算流冰撞击荷载是合理可行的.
2 桥梁撞击减振控制
2.1 结构模型及动力特性分析
以高速铁路3×32 m简支梁为例,研究TMD对冰击荷载作用下桥梁振动的减振特性.采用ANSYS建立桥梁有限元模型,截面参考图2所示,墩高25 m.主梁和桥墩采用solid65单元模拟,桥面二期恒载作为附加质量分布到桥面上,取值184 kN/m.主梁和支座,桥墩与基础的连接采用combin14单元模拟,该力元可以有效模拟支座和基础的刚度和阻尼特性,桥梁有限元模型如图6所示.
图6 桥梁有限元模型Fig.6 Finite element model of the bridge
对上述有限元模型进行模态分析,因流冰撞击桥墩主要影响桥梁的横向振动,因此本文只分析桥梁横向振动模态,图7所示为桥梁前3阶横向振型.
2.2 TMD最优参数设计和最佳安装位置
由公式(5)可知,当节点j位于桥梁模态最大位移处时,得到的模态等效质量Mij最小,TMD质量比最大;当节点j位于桥梁模态变形为0处时,模态等效质量Mij无穷大,TMD质量比为0.由TMD设计理论可知,系统能量耗散程度与TMD质量比成正比,即TMD质量比越大,振动衰减越快.因此,TMD的最佳安装位置为桥梁所控模态的最大位移处[19].
流冰撞击桥墩会使墩身和主梁的横向位移增大,严重时会影响桥梁结构安全性和桥上列车运行安全性,因此TMD设计以减少桥梁结构横向位移为主.考虑到流冰撞击的最不利工况,将计算获得的流冰撞击荷载以外激励的形式输入到所有桥墩上,荷载施加位置为距墩底5m处.图8所示为冰击荷载作用下桥梁第二跨跨中和3号墩顶横向位移时程曲线和幅频曲线.

图7 桥梁前三阶横向振型Fig.7 First three lateral mode shapes of the bridge
由图8可知,冰击荷载作用下,桥梁跨中和墩顶横向位移急剧增大,冰击荷载主频与桥梁跨中和墩顶横向位移主频相同,且与桥梁结构二阶横向振动频率接近,这可能激发桥梁结构更大的振动.因此,以控制桥梁结构二阶横向振动模态为目标设计TMD系统,由图7可知,桥梁二阶横向振型为墩梁反对称横移,墩顶处模态位移最大,因此TMD安装在桥梁墩顶处,每个墩顶安装一个TMD.表2所示为TMD在不同质量比下的最优参数.
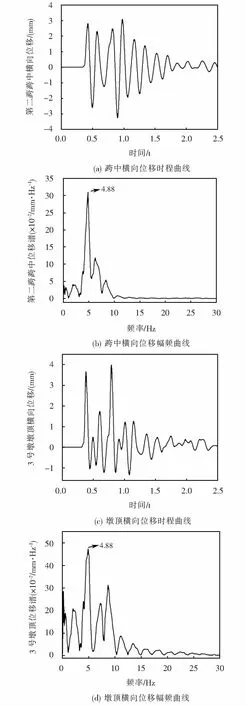
图8 冰击荷载作用下桥梁横向位移时程曲线和幅频曲线Fig.8 Time history and frequency spectrum of the bridge lateral displacement under floating ice collision

表2 不同质量比下TMD最优参数
2.3 TMD减振特性分析
针对所设计TMD系统,分析流冰撞击作用下不同质量比TMD对桥梁振动抑制特性的影响.图9所示为不同质量比的TMD对冰击荷载作用下桥梁横向位移的减振控制效果.
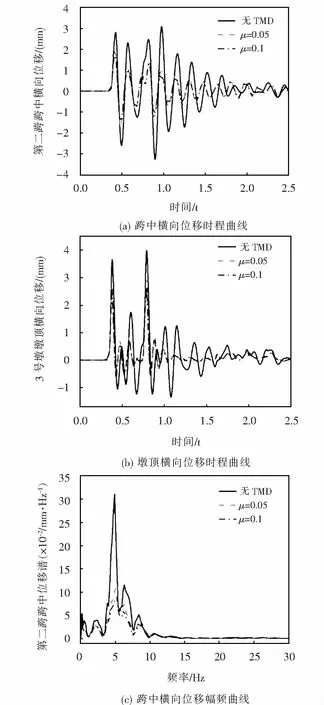
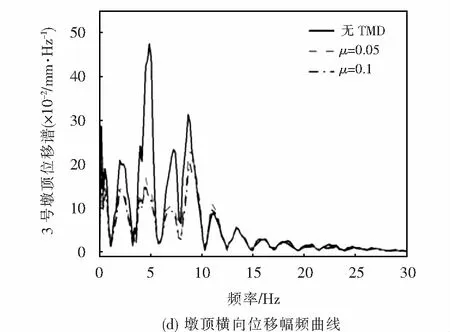
图9 不同质量比TMD作用下桥梁横向位移抑制效果Fig.9 Suppression effect of bridge lateral displacement under different mass ratio of TMD
由图9(a)~(b)可知,TMD对桥梁跨中和墩顶横向位移抑制明显.增大TMD质量比后,桥梁跨中和墩顶横向位移减小,但减小幅度较小.当TMD质量比μ=0.05时,桥梁跨中和墩顶横向位移峰值分别降低45.4%和31.8%,当TMD质量比增大到μ=0.1时,桥梁跨中和墩顶横向位移峰值分别降低49.1%和35.6%.由图9(c)~(d)可知,TMD显著降低了桥梁跨中和墩顶横向位移主频峰值.结果表明,TMD能有效抑制冰击荷载作用下桥梁跨中和墩顶横向位移,减振效果明显.
图10所示为冰击荷载作用下桥梁跨中和墩顶横向振动加速度时程曲线和幅频曲线.由图可以看出,TMD对冰击荷载下桥梁跨中和墩顶横向振动加速度也有一定的抑制作用,但减振效果没有横向位移减振效果明显.桥梁跨中和墩顶横向振动加速度随TMD质量比的增加而减小,当TMD质量比μ=0.05时,桥梁跨中和墩顶横向加速度峰值分别降低12.1%和10.3%,当TMD质量比μ=0.1时,桥梁跨中和墩顶横向加速度峰值分别降低18.6%和14.2%.
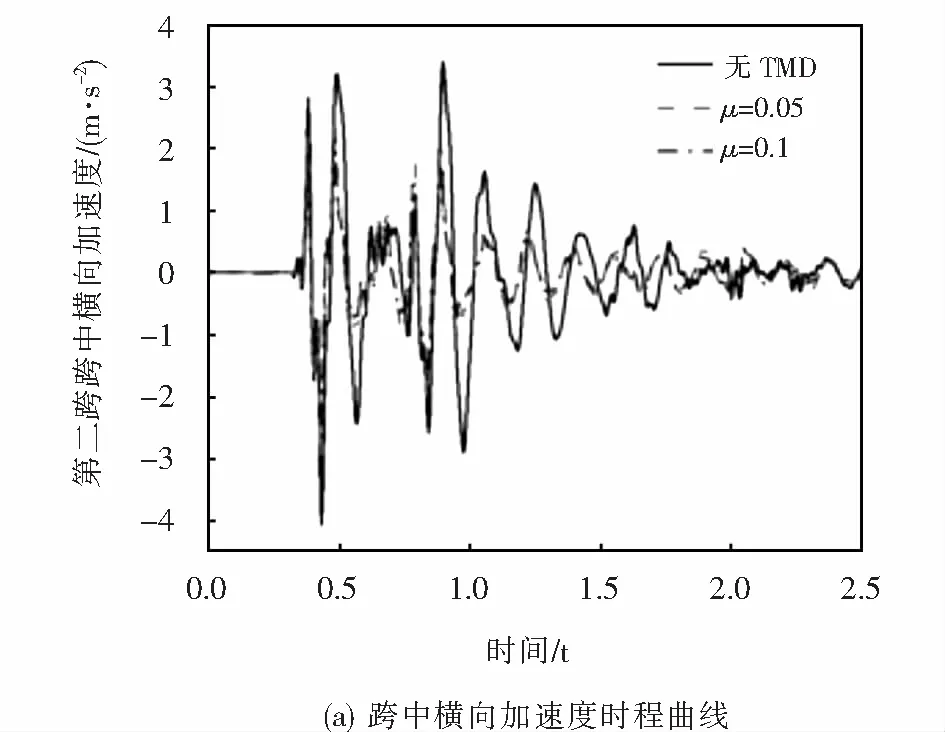
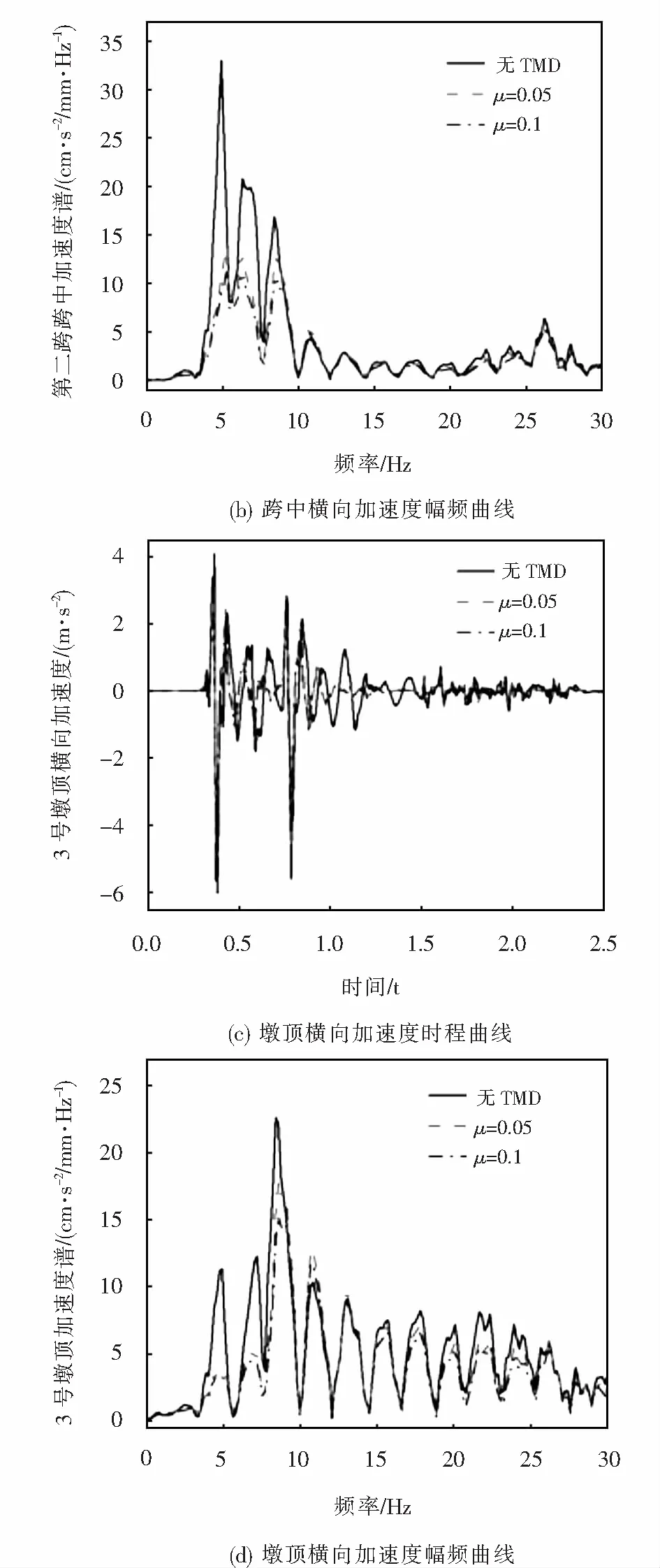
图10 桥梁结构横向加速度减振效果Fig.10 Vibration reduction effect of the bridge lateral acceleration
3 结论
基于TMD设计理论和有限元方法,建立了考虑流冰撞击影响的桥梁结构-TMD减振控制系统,研究了不同质量比TMD对冰击荷载作用下桥梁跨中和墩顶横向位移和横向加速度的影响,得出以下结论:
1) 基于传递函数法和动能理论可以准确得到TMD的最优刚度、阻尼和最佳安装位置;TMD的最佳安装位置为桥梁墩顶处.
2) 有限元方法计算的冰击时程力峰值,与规范中冰击力计算公式的计算结果误差仅4.7%,说明采用有限元模型计算流冰撞击荷载是合理可行的.
3) TMD显著降低了桥梁跨中和墩顶的横向位移,对桥梁横向位移频谱的影响也较大;增加TMD质量比,桥梁横向振动减振效果增大;TMD对桥梁横向振动加速度也有一定的抑制作用,但抑制效果没有对横向位移明显.
