泗阳桃源大桥抗风性能数值模拟研究
2021-04-28朱奎笑
朱奎笑
(泗阳县公路事业发展中心,江苏宿迁223799)
0 引言
21世纪以来,随着桥梁设计理论、高性能材料、施工技术的飞速发展,现代桥梁建设日益向大跨径、高柔度、低阻尼比方向发展,导致大跨结构对风的敏感程度大大增加,桥梁抗风问题往往成为超大跨桥梁设计中的控制性因素。风对桥梁的动力作用主要包括颤振、涡振、抖振、驰振四种类型,其中桥梁颤振是一种失稳发散振动,一旦发生将会导致结构的整体倒塌,自美国塔科马大桥颤振倒塌之后,桥梁颤振失稳问题引起了桥梁工程界的高度重视。
目前桥梁结构抗风性能分析研究主要采用三种方法:理论分析法、物理风洞试验法、数值模拟方法。何旭辉等分别通过节段模型风洞试验及全桥气弹模型风洞试验研究大跨径桥梁的颤振稳定性、涡激共振响应、结构静气动力系数等,研究表明,采用物理风洞缩尺模型试验能够准确地反映出结构在风荷载作用下的响应。但是物理风洞试验仍然存在一些弊端,如试验周期长、试验室建设成本高、测试设备复杂、结构周围风场流动无法可视化等。随着计算机技术的发展以及计算流体动力学理论(Computational Fluid Dynamics,CFD)的不断改善,CFD 数值模拟成为一种可以替代物理风洞试验的计算方法。该方法是通过计算机数值计算和图像显示,对包含有流体流动和热传导等相关物理现象的系统分析。其基本思想是把原来在时间域及空间域上连续的物理量的场,用一系列有限个离散点上变量值的集合来代替,通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组,然后求解代数方程组获得场变量的近似值。杨风帆、石亚光采用CFD 数值模拟方法研究了大跨桥梁非线性气动力并对主梁涡激共振诱因展开了分析;战庆亮等采用数值模拟方法获取了主梁断面气动导数,并与试验结果进行对比,分析了试验与数值模拟方法的优势与不足。文献调研表明,相比于物理风洞试验,CFD 数值模拟计算方法可以大大降低成本,提高效率,而且可以更加直观地显示结构周围流场的变化。但是数值模拟方法的准确性与建立的离散化模型及相关参数的选取有关,且该方法不能直接用于模拟全桥气弹模型风洞试验。
本文基于泗阳桃源大桥开展主桥结构颤振稳定性数值模拟分析。首先,建立全桥结构鱼骨式杆系有限元模型,并获取结构各阶特征振型频率及模态;其次,采用数值模拟分析方法获取主梁断面不同折减风速下的气动导数;最后,采用PK-F 三维颤振稳定性分析方法进行各个风攻角下的主梁颤振稳定性分析。结果表明:各个风攻角下主梁的颤振稳定性满足规范要求。本文的研究思路可以为大跨桥梁结构颤振稳定性数值模拟分析提供借鉴。
1 工程概况
京杭运河泗阳桃源大桥是《泗阳城市总体规划(2011—2030)》中规划的城市主干路桃源南路的重要组成部分,是泗阳县干线交通网中的重要通道,下跨京杭大运河[1]。主桥采用全漂浮体系独柱混凝土塔钢箱梁斜拉桥,跨径布置为45+36+34+385+34+45+36=615m。结构主跨断面采用整体式钢箱梁截面,边跨主梁采用整体式混凝土箱梁截面,两种截面外形完全相同。箱梁梁高为3.0m,桥面宽度为40.6m,桥面设计为双向六车道,并配有人行道、非机动车道。桥塔采用100m 高度的中央独柱形混凝土塔[2]。顺桥向桥塔形似水滴或宝瓶。主桥结构总体立面布置及主梁断面如图1所示。
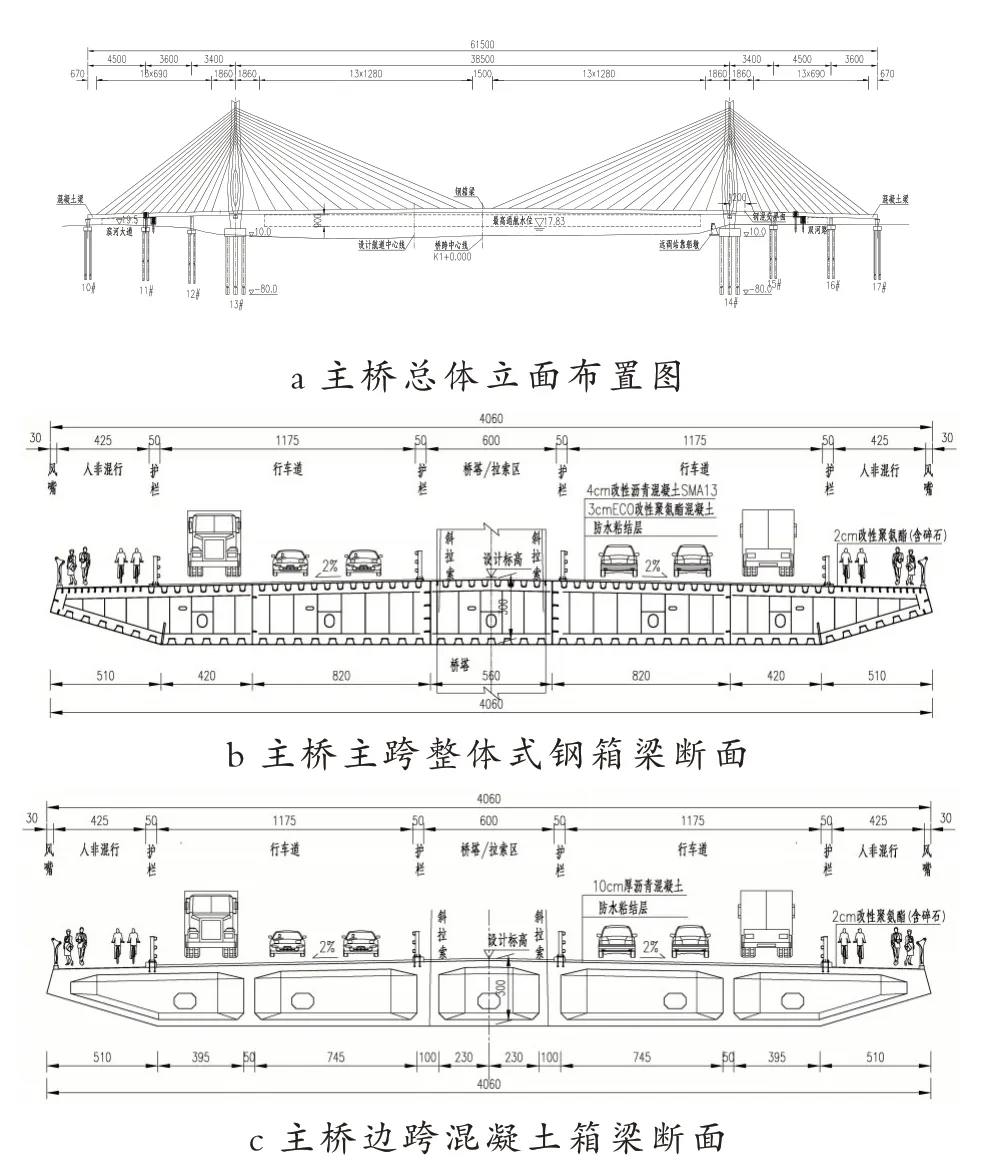
图1 结构立面布置及主梁截面(单位:cm)
根据《公路桥梁抗风设计规范》(JTG/T 3360-01—2018),桃源大桥桥位处标准高度10m、平均时距10min、重现期100年的基本风速可以按照规范附录A中宿迁市地区风速取值为26.7m/s。根据规范第7.5.8 条规定,计算得到主桥成桥状态颤振检验风速为46.5m/s。
2 结构动力特性分析
2.1 有限元模型建立
桥梁结构动力特性分析是研究桥梁风致振动问题的基础,为开展主梁抗风性能虚拟风洞试验研究,必须先进行结构的动力特性分析[3]。采用通用有限元软件建立桃源大桥全桥结构鱼骨式杆系有限元模型,整体坐标系统以顺桥向为X 轴、竖向为Y 轴、横桥向为Z 轴。全桥共542 个节点,825 个单元,全桥结构的有限元模型及主梁支座处边界约束条件如图2、图3所示。其中,主梁、桥塔、斜拉索与主梁、桥塔连接刚臂均采用BEAM4 单元模拟,BEAM4 单元是一种可以承受拉、压、弯、扭的单轴受力单元,单元每个节点具有六个自由度,单元截面特性通过输入实常数定义;斜拉索采用LINK10 单元模拟,LINK10 单元是三维仅受拉或者受压单元,单元两端节点仅有三个平动自由度,初始拉力通过实常数赋予初始应变[4]。在建立斜拉索模型时,需要考虑长拉索的等效弹性模量,采用Ernst 公式计算拉索单元换算弹性模量[5],见下式(1)。桥面二期恒载质量分布采用MASS21 单元模拟,MASS21 单元是一种具有六个自由度的点元素,只有一个节点,通过实常数定义六个自由度方向的质量及质量惯矩[6]。
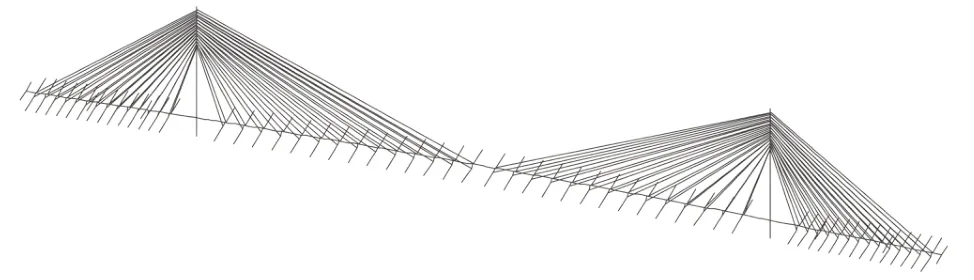
图2 全桥结构杆系有限元模型
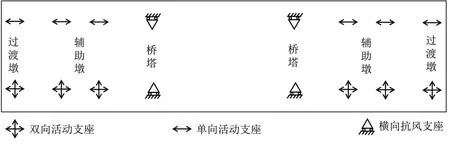
图3 全桥主梁支座处边界条件
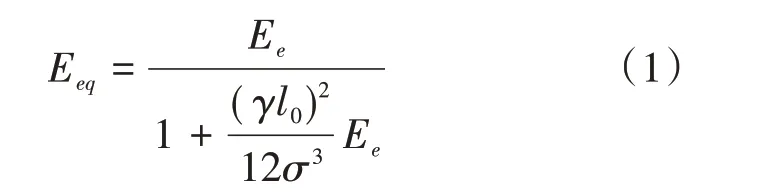
式(1)中:Eeq为斜拉索的等效弹性模量;Ee为钢丝的弹性模量;γ为钢丝重度;l0为斜拉索水平投影长度;σ为斜拉索应力[7]。
2.2 动力特性分析
考虑斜拉索的等效弹性模量及初始应变,采用子空间迭代法计算全桥结构各阶自振特性及振型模态,并获取结构各阶振型等效质量见表1。图4 为各阶模态振型图。

表1 各阶振型频率及等效质量
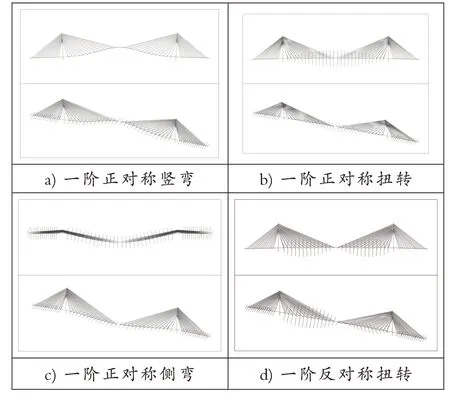
图4 结构各阶特征模态振型图
3 结构虚拟风洞试验研究
3.1 主梁气动导数数值模拟
流体运动需要满足连续方程、动量守恒方程、能量守恒方程。以上三个方程统称为Navier-Stokes 方程,方程表达式分别如下式(2)~(4):
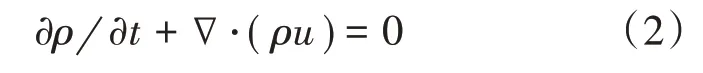
式(2)中:ρ为流体密度;u为速度分量;∇·为散度。

式(3)中:ρ为压力;μ为流体运动黏度系数;Su为动量守恒方程广义源项;∇为梯度。

式(4)中:T为温度;cp为比热容;k为流体传热系数;ST为流体的内热源及由于黏性作用流体机械能转换为热能的部分[8]。
本文流场的数值模拟以上述Navier-Stokes 方程为基本控制方程,采用离散化的数值模拟方法求解流场[9]。在Navier-Stokes 方程求解中,采用直接数值求解可精确描述绕流流动,但对三维高雷诺数绕流流动,这种数值模拟的计算量是难以承受的,在工程上常采用湍流模型来计算[10]。湍流模型是模拟均值化的流场,对难以分辨的小尺度涡在均值化过程加以忽略,而被忽略的小尺度涡在湍流模型中体现[11]。本研究采用基于时间平均的雷诺均值Navier-Stokes 方程模型中使用最广泛的Realizablek-ε双方程湍流模型[12]。
数值模拟分析模型中流体入口边界条件采用均匀来流10m/s 的速度进口,出口边界条件为压力出口边界条件[13]。主梁气动导数分析断面采用成桥状态断面,包括主梁外形、防撞栏杆、检修轨道等纵向通长的构件,如图5所示。通过数值风洞大涡模拟方法模拟气流的瞬态流动,从而获得不同风速下主梁断面以不同固定频率作竖向及扭转强迫振动的周围流场变化及断面所受风荷载的变化时程曲线,并利用最小二乘法识别不同折减风速下对应的主梁气动导数[14]。数值风洞模拟断面不同风攻角下的流场图如图6所示。

图5 主梁CFD 数值模拟分析断面

图6 各风攻角下主梁断面流场示意图
CFD 数值模拟得到的主梁断面不同折减风速下对应的8 个气动导数如图7~图9所示,得到的气动导数可用于三维主梁断面颤振稳定性分析。其中折减风速U*的计算见下式(5)。

图7 -3o 风攻角下主梁断面气动导数

图8 0o 风攻角下主梁断面气动导数
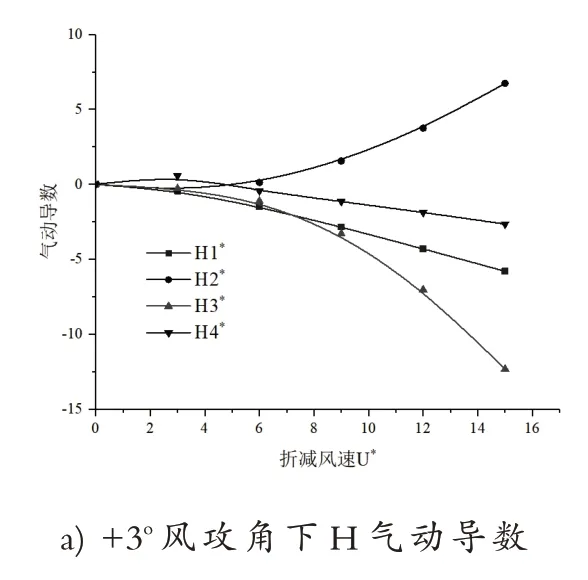
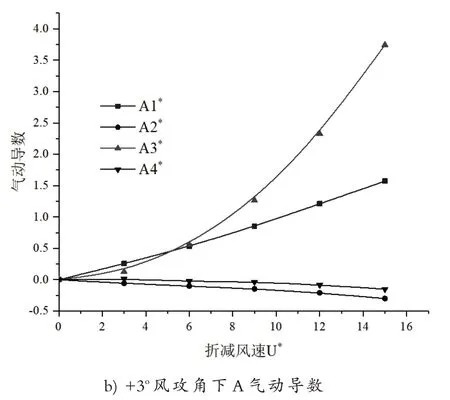
图9 +3o 风攻角下主梁断面气动导数

式(5)中:U为桥址处对应的实际风速;f为主桥结构特征振型频率,包括竖弯及扭转;B为主梁宽度。
3.2 颤振稳定性分析
本文研究通过建立三维的结构振动方程,引入PK-F 数值处理方法求解颤振方程。选取结构对称竖弯及扭转振型频率及模态进行分析,经求解可获得竖弯及扭转振型在不同风速下的对数衰减率及对应振型频率。当对数衰减率为正时,结构发生颤振失稳现象[15]。该算法具有很好的收敛性,能够比较清楚地反映颤振前后过程系统状态的变化。基于主梁断面的气动导数,采用此方法开展主桥成桥状态下各风攻角下颤振稳定性分析。由于颤振失稳多表现为扭转发散失稳,为缩减篇幅,在此只列出各风攻角下主梁扭转对数衰减率随折减风速的变化曲线,如图10所示。由图可以发现,在各风攻角下主梁扭转对数衰减率随风速的变化趋势为先逐渐减小然后迅速增大,直至大于0 出现扭转颤振失稳[16]。对数衰减率后期增加的速率明显大于前期逐渐减小的速率,即结构的扭转发散失稳具有短时突发性[17]。
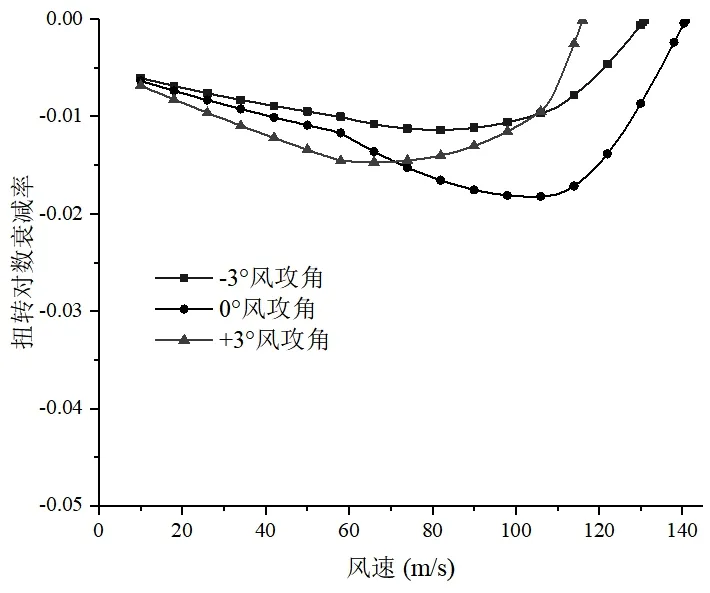
图10 各风攻角下主梁扭转振型对数衰减率随风速的变化
由上述方法计算得到主桥结构成桥状态各风攻角下扭转颤振失稳临界风速见表2,可见桃源大桥成桥状态正对称扭转模态颤振最不利状态对应+3o风攻角,颤振临界风速为116.1m/s,高于颤振检验风速46.5m/s,故主桥颤振稳定性检验满足规范要求。

表2 各风攻角下扭转颤振失稳临界风速(单位:m/s)
4 结语
本文基于泗阳桃源大桥建立全桥结构杆系有限元模型,并获取结构各阶特征振型频率及模态;然后采用CFD 数值模拟方法获取各风攻角下主梁断面不同折减风速的气动导数;最后采用PK-F 三维颤振稳定性分析方法开展主梁颤振稳定性分析。研究表明:扭转对数衰减率随风速的增加呈先减小然后迅速增大的趋势,结构的扭转发散失稳具有短时突发性。各个风攻角下主梁的颤振稳定性均满足规范要求。
