基于bagging算法的经济金融数据分析

2021-04-28任雪妮罗幼喜

湖北工业大学学报 2021年2期

任雪妮，罗幼喜

(湖北工业大学理学院，湖北武汉 430068)

单个分类的学习效果有时候并不是很理想，为了解决这个问题，集成学习算法由此产生。集成学习并不是单指某一种分类器，而是充分利用了群体学习思想，将一个或多个弱分类器结合成一个强分类器的一种方法，其中的弱分类器可以是各种分类算法。常使用的集成学习方法有bagging和boosting(本文主要使用bagging算法)[1]。对于集成算法是否真的比单个分类器具有更高的准确性，不少学者进行了研究。David和Richard[2]使用决策树和神经网络分别研究了bagging和boosting两种集成方法，还与单个分类器方法进行比较；Michiel和Rob[3]的研究包含bagging集成在内的4种方法。这些学者发现集成学习算法的效果的确是好于单个分类器。

由于集成算法的优良性，也有不少学者使用集成算法进行实际应用，特别是在经济金融领域。Mariola等[4]采用集成方法对信用卡借款者进行了识别；Atsushi和Lutz[5]探讨了bagging方法在预测经济时间序列中的作用；Choprab和Bhilare[6]使用集成树学习方法对银行贷款数据集进行分析。

经济金融领域一直以来都受到学者们的关注。本文对经济金融领域的数据集进行分析，选择C5.0决策树、KNN和朴素贝叶斯算法作为bagging算法的基本算法，针对每个数据集，从所构造的几种bagging方法中选取预测效果最好的方法对其进行实例研究。

1 算法的基本思路及原理

1.1 Bagging算法

Step1：采用Bootstraping方法从训练集中随机进行k次抽取，每次抽取的训练集的样本个数与本文设置的原始训练集样本数相同。

Step2：使用k个弱分类器对k个训练集分别进行训练，可以得到k个模型。此处的分类器可以是一个或多个分类算法。

Step3：对k个模型采用投票方式即可得到分类结果，在投票过程中，每个模型给与的权重相同。

图1显示了Bagging算法的具体过程。

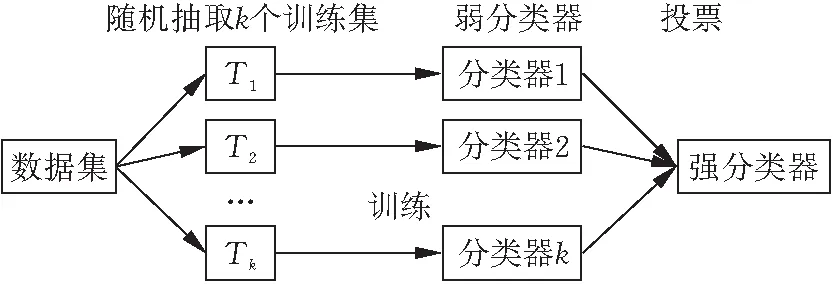
图1 bagging算法过程

1.2 KNN算法

Step1：计算测试集中每个样本点与训练集中所有样本点的距离，并对测试集中的每个样本点所得的距离进行排序。

Step2：测试集中的每个样本点选择训练集中与其距离最小的k个点，并确定前k个点所在类别的出现频率，以出现频率最高的类别作为测试集样本点的预测分类。

1.3 C5.0决策树算法

Step1：计算各输入变量的信息增益率，以信息增益率最大的变量为最佳分组变量。若分组变量为k类分类变量，则形成k个分枝。若为数值型，则用分箱法进行处理后再分枝。

Step2：计算各节点误差，若子节点误差大于其父节点误差，则进行剪枝。

1.4 朴素贝叶斯算法

对于分类数据集，给定样本自变量x，则该样本属于类别y的概率

朴素贝叶斯算法[8]的原理就是根据以上公式，计算出每个样本属于各分类的概率，概率最大的那个分类即为预测分类。

2 模拟分析

从UCI网站上获取了4个数据集，将其简记为credit，bank，stock，audit。数据集credit根据用户的一些属性来判断用户能否用信用卡进行贷款。在该数据集中存在缺失值，缺失值处理方法是用0填补。数据集bank主要是银行机构通过电话推销的一款银行定期存款产品是否会被订购。数据集stock主要是根据以往数据预测下一周股票价格变化情况。数据集audit是印度审计办公室收集的关于一些公司的数据，主要是根据一些重要的风险因素来判断这些公司是否有变成可疑公司的风险，bank，stock，audit数据集中无缺失值。表1为这些数据集的基本情况。

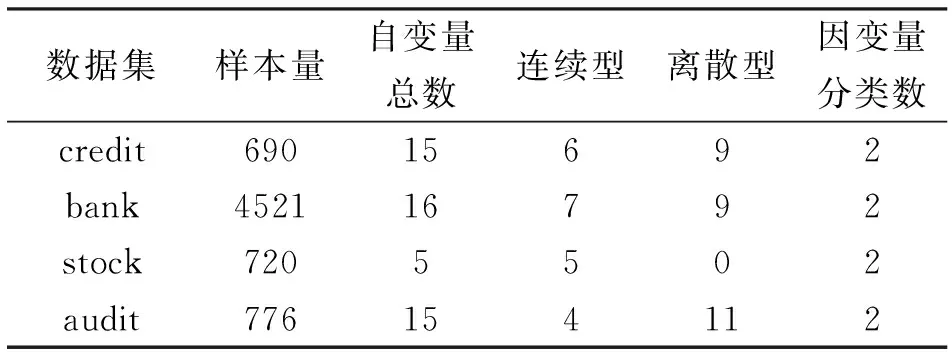
表1 数据集

为了评价预测的准确度，将使用混淆矩阵中的指标，混淆矩阵的具体形式如表2所示。

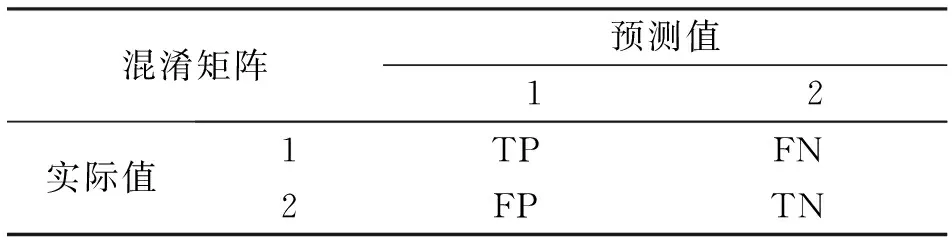
表2 混淆矩阵

TP(True Positive)，表示响应变量实际分类为1，预测分类也为1；

FN(False Negative)，表示响应变量实际分类为1，预测分类却为2；

FP(False Positive)，表示响应变量实际分类为2，预测分类却为1；

TN(True Negative)，表示响应变量实际分类为2，预测分类也为2；

准确率(Accurary)，表示所有分类正确的数量占总样本量的比例，其具体公式为：

在进行评价时，使用预测误差Err(error)来判断模型预测的好坏，其计算公式为：

Err=1-ACU

2.1 模拟一

选取KNN、C5.0决策树、朴素贝叶斯三种经典的分类算法，对它们采用单类、两两混合、三种混合形式构造了7种组合方法，分别简记为bag_k，bag_c，bag_b，bag_kc，bag_kb，bag_cb，bag_kcb。为了研究弱分类器的个数对bagging算法所得到强分类器预测准确性的影响以及credit，bank，stock和audit数据集最合适的分类器的个数。设置弱分类器个数分别为R=10，R=20，R=50。各个方法中3种分类器具体设置个数见表3。

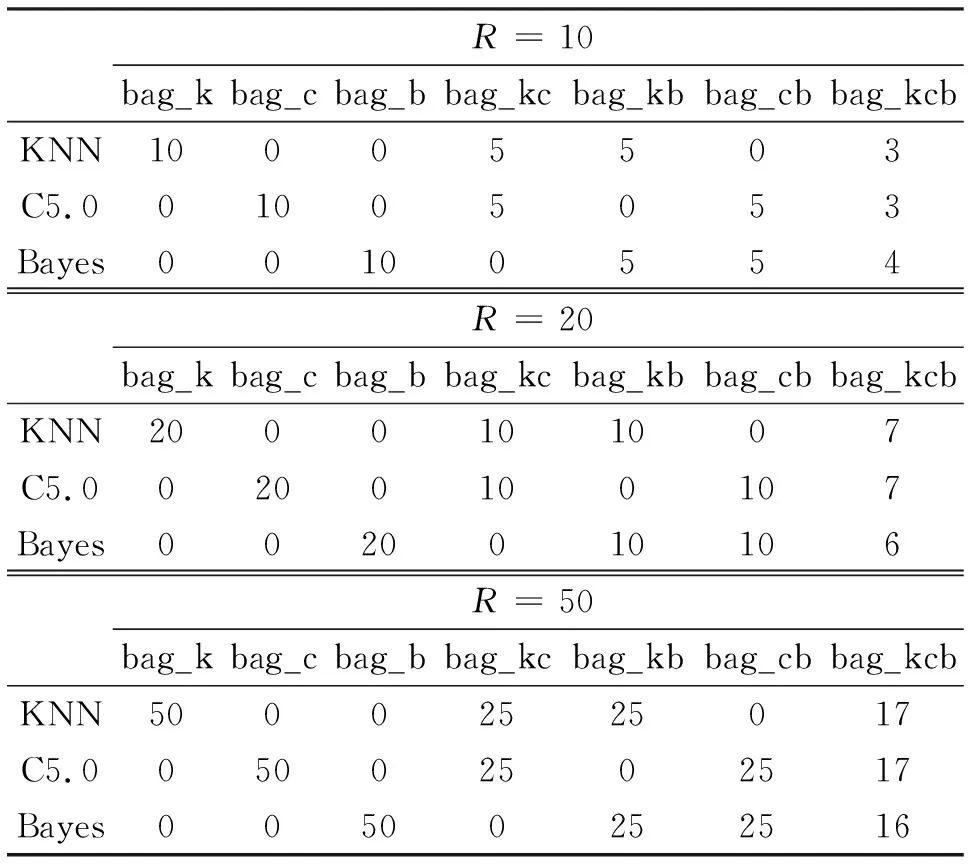
表3 分类器个数设置情况

credit，bank，stock和audit数据集重复模拟100次后得到预测误差的结果如表4所示。从表4可以知道，在credit数据集中，使用bag_k，bag_c，bag_kc，bag_kcb方法得到的预测误差在R=50时最小，其他三种方法在R=20时最小。

在bank数据集中，使用bag_k，bag_c，bag_b，bag_kc方法得到的预测误差在R=20时最小，bag_kb方法在R=10时最小，而bag_cb和bag_kcb方法在R=50时最小。

在stock数据集中，bag_k和bag_cb方法得到的预测误差在R=10时最小，bag_c，bag_b和bag_kb方法在R=50时最小，bag_kc和bag_kcb方法在R=20时最小。

在audit数据集中，bag_k方法得到的预测误差在R=20时最小，bag_c，bag_b，bag_kb，bag_cb，bag_kcb在R=50时最小，而bag_kc方法在R=20和R=50时都最小。

从研究的几种情况看，所使用的7种方法在预测误差达到最小时所使用的弱分类器的个数有所区别，即弱分类器的个数对bagging算法所得到强分类器预测准确性有影响。在credit，stock和audit数据集中，R=50是7种方法中使预测误差达最小时出现频率最高的分类器个数。而在bank数据集中，出现频率最高的分类器个数为R=20。综合来看，R=50是使预测误差达最小时出现频率最高的分类器个数。

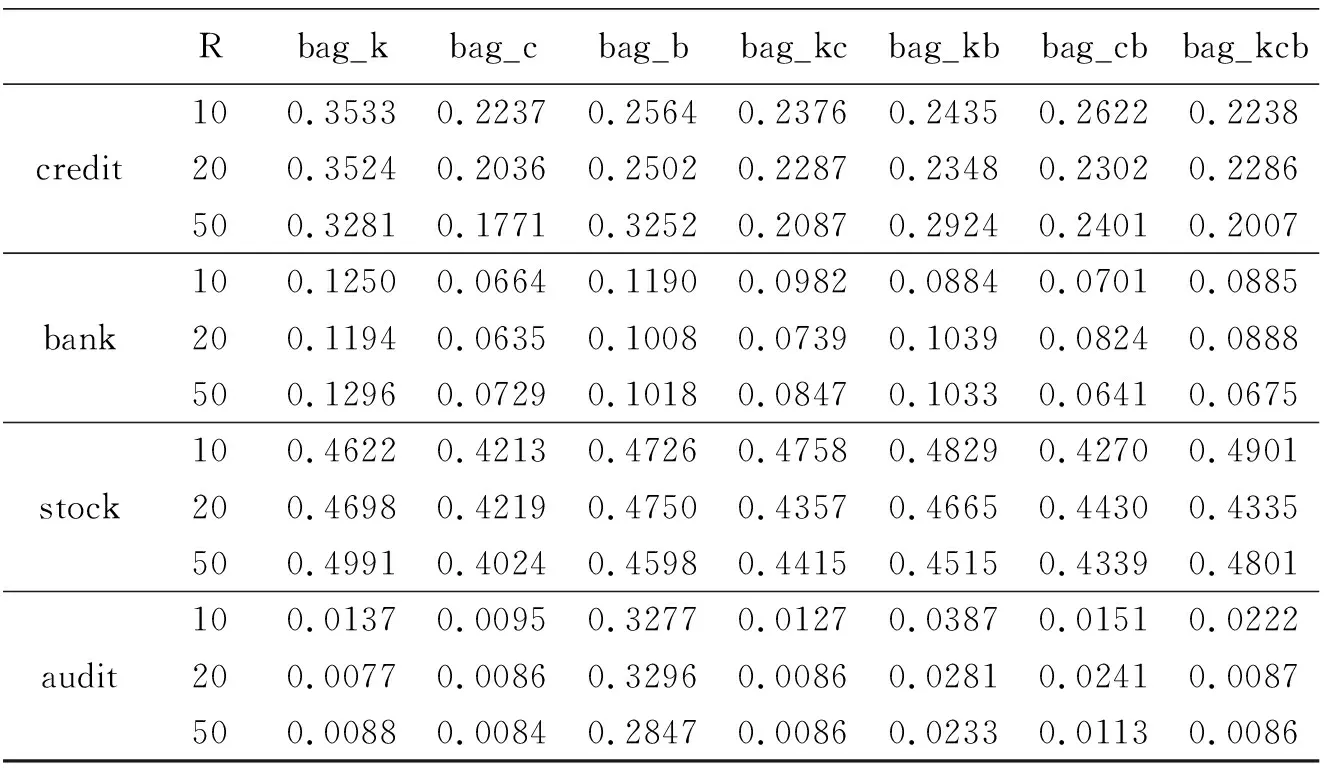
表4 分类器个数不同的模拟结果

2.2 模拟二

为了研究弱分类器的构成种类对bagging算法所得到强分类器预测准确性的影响以及credit，bank，stock，audit数据集最合适的分类器组合方法，7种方法设置同样的分类器个数，然后对比7种方法下所得到预测误差情况。通过模拟一的研究可以知道，在此模拟中设置分类数个数R=50是比较合适的。对4个数据集重复模拟100次后得到预测误差的结果如图2所示。

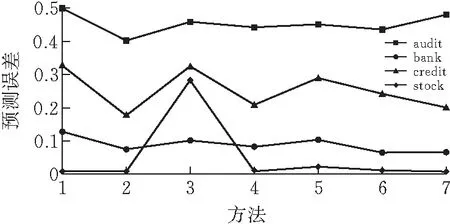
图 2 四个数据集下各方法预测结果

图2中横坐标1-7分别对应bag_k，bag_c，bag_b，bag_kc，bag_kb，bag_cb，bag_kcb等7种方法。在credit和stock数据集中，使用bag_c方法得到的预测误差最小，bag_k方法预测误差最大；在bank数据集中，bag_cb方法得到的预测误差最小，预测误差最大的是bag_k方法；在audit数据集中，bag_c方法得到的预测误差最小，预测误差最大的是bag_b方法。

弱分类器的构成种类对bagging算法所得到强分类器预测准确性有影响而且除了bank数据集，其他3个预测结果最好的是使用bag_c方法。总的来看，bag_c方法这种弱分类器构成种类能得到更好地预测误差结果。从bag_k，bag_c，bag_b这3种方法的模拟结果来看，只有一种分类器构造的bagging方法中使用C5.0决策树的结果总是最好的。这也说明bagging算法构成的分类器的准确性与其弱分类器的性能有较大关系。

2.3 综合分析

通过模拟一和模拟二的分析可以看到，数据集的不同，构成bagging算法的方法和弱分类器个数会有一些细微差别。为最终确定credit，bank，stock和audit数据集最合适的分类器组合方法所选取的4个数据集分别拥有不同的数据特点：

credit，小数据集且离散和连续型自变量个数相差不大；

bank，大数据集且离散和连续型自变量个数相差不大；

stock，小数据集且只有连续型自变量；

audit，小数据集且离散自变量个数远多于连续型。

结合模拟一和模拟二对这4个数据集进行集中讨论分析，以此来确定最适合这4个数据集的方法和分类器个数。

根据模拟一数据来分析，对于credit和stock数据集，所有情形都是使用bag_c方法得到了最小预测误差，即这两个数据集更适合使用bag_c方法来进行测试。对于bank和audit数据集，在分类器个数不同的3种情形中有2次使用bag_c方法得到了最小预测误差，即这2个数据集也更适合使用bag_c方法来进行测试。

而且根据模拟一的分析知道，credit，stock，audit数据集都可以让R=50作为预测误差达最小时出现频率最高的分类器个数。对于bank数据集，使预测误差达最小时出现频率最高的分类器个数是R=20。除了bank数据集，在模拟二中其他三个预测结果最好的是使用bag_c方法，但当bank数据集选择分类器个数为R=20时，使用bag_c方法能够得到最佳的预测结果。可以确定最适合这4个数据集方法和分类器个数情况如表5所示。

表5 四个数据集最佳组合

credit，bank，stock和audit这4个数据集无论数据特性如何，使用bag_c方法都可让其预测误差达到最小，但使用的分类器个数却有一定差别，bank数据集样本量最大，使预测误差达最小时所需要的分类器个数却比其他三个数据集在预测误差达最小时所用的分类器个数少。

3 实例分析

bank数据集涉及的是银行机构推销的一款银行定期存款产品是否会被订购。若银行定期存款产品没有被用户订购，此处设置为类别1，否则为类别2。自变量的变量名及其具体含义如表6所示。

对该数据集使用bag_c方法，并设置分类器个数为R=20，可以得到其测试集的混淆矩阵如表7所示。从表7可以知道，测试集中的样本数据量为1356。实际用户对银行定期存款产品订购情况类别为1的有1266位，但其中有66位用户的订购情况被误判为类别2。对于类别1而言，其判断正确的准确率为94.79%，即在没有订购银行定期存款产品的用户中，有94.79%的用户被预测正确。可以看到其准确率比较高，这样不会错失过多的没有订购的用户。对于没有订购的用户可以继续进行推销，有可能会推销成功。而实际用户对银行定期存款产品订购情况类别为2的有90位，其中有13位用户的订购情况被误判为类别2。对于类别2而言，其判断正确的准确率为85.56%，即在已经订购银行定期存款产品的用户中，有85.56%的用户被预测正确。虽然对成功订购用户的预测准确性一般，但是对于该次推销活动的结果影响不大。最终计算可得到bank测试集中所有数据的预测误差Err=0.0583。即bag_c方法对于此数据集的准确性达到94.17%，可以看到预测的准确性还是不错的。

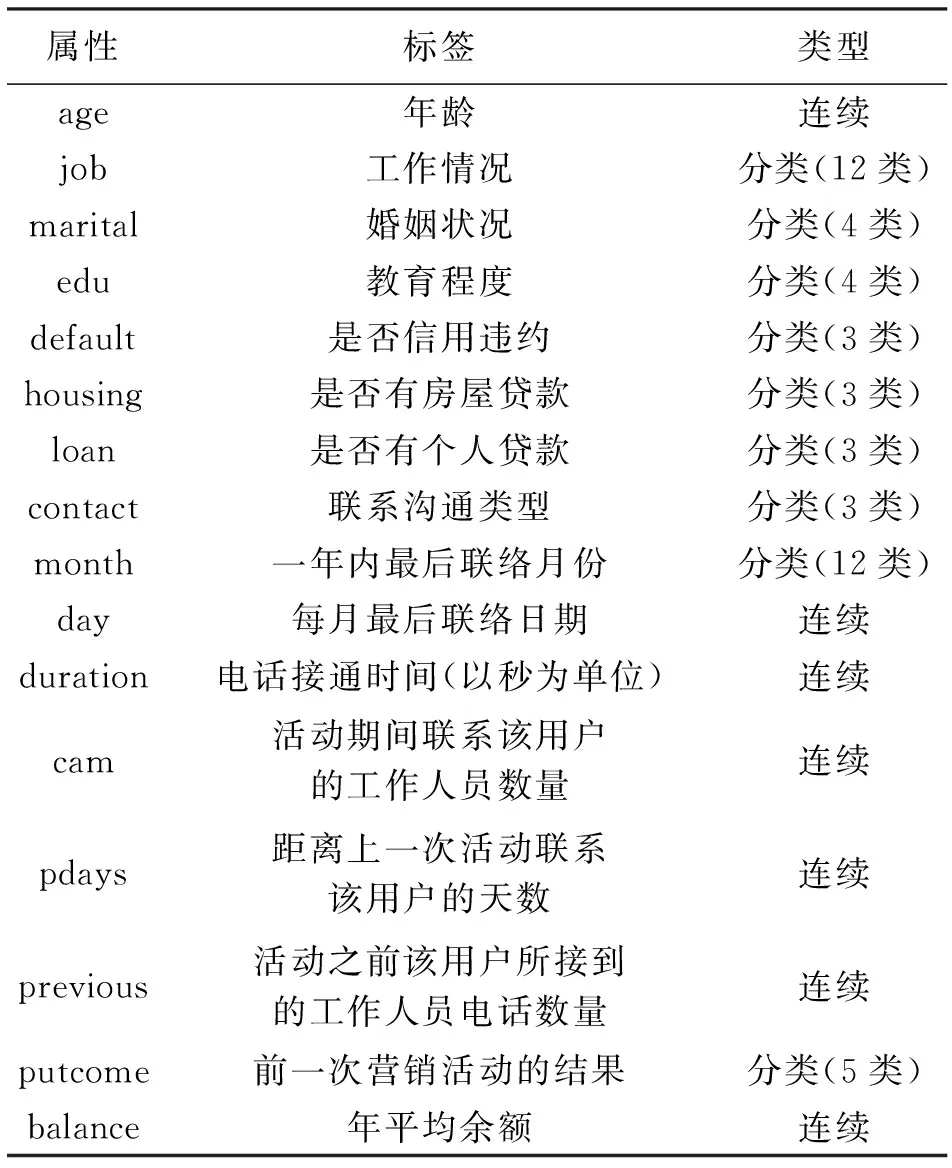
表6 bank数据集自变量解释

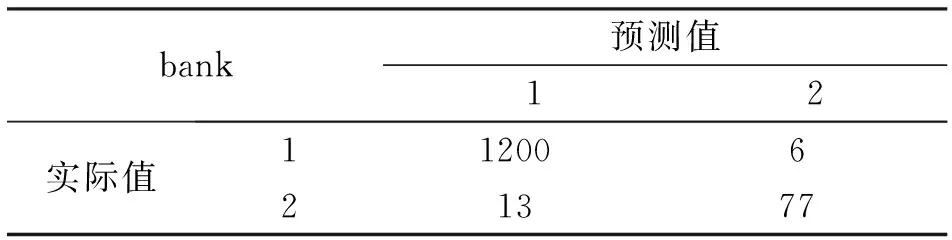
表7 bank测试集的混淆矩阵

给出了bank数据集在用bag_c方法进行预测分类时各自变量的重要程度，具体情况如图3所示。

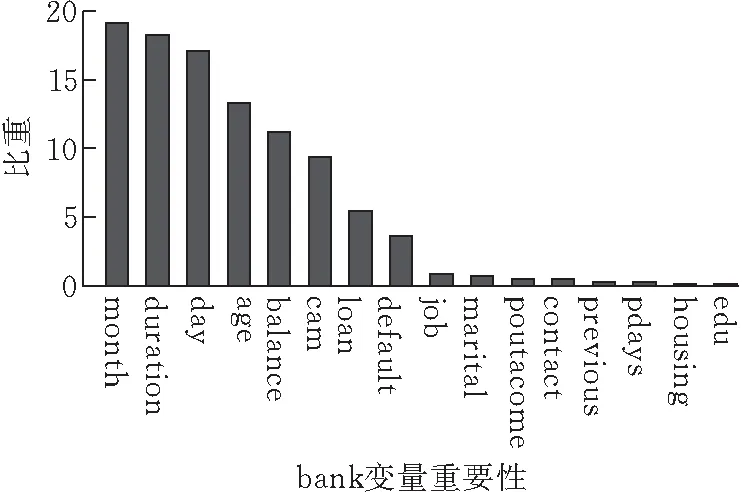
图 3 bank数据集中自变量重要性

从图3中可以看到，previous，pdays，housing和edu这4个变量的重要程度所占比重非常小，几乎可以忽略不计，即使用bag_c方法对bank数据集进行测试所得到的预测结果与用户的这4个属性无关。而month，duration，day，age和balance这5个变量的重要程度所占比重为前5，且它们的重要程度所占比重都超过了10%。由图3可知：month和day这2个变量说明选择联系用户的时间节点很重要；duration这个变量说明与用户通话时间的长短也影响用户是否会订购产品(毕竟用户不想订购是不会有太多耐心长时间通电话)；age这个变量说明用户的年龄也会对产品的推销结果产生较大影响，现实生活中不同年龄阶段的人对于是否将钱进行理财也有不同见解；同样balance这个变量也说明用户每年所剩的平均余额会影响其是否会订购银行产品，毕竟用户有多余的钱才可能考虑投入银行理财，与事实情况也很接近。