基于事件驱动的航天器姿态自适应跟踪控制*
2021-04-27林子杰陆国平吴宝林
林子杰 陆国平 吕 旺 吴宝林
1.上海卫星工程研究所,上海 201109 2.哈尔滨工业大学卫星技术研究所,哈尔滨150001
0 引言
近年来,低成本的即插即用小型航天器受到广泛关注。即插即用技术简化各个模块的安装,各个模块间通过无线网络连接。无线通信相较传统电缆通信有许多优点,但低成本的小型航天器在无线的数据传输网络中更容易造成数据丢失和时延的现象。因而,各个模块之间数据交互带来的通信带宽受限必须在卫星分系统设计阶段就要考虑[1]。
将通信资源约束与航天器姿态控制结合,过去学者们提出了诸如输出反馈控制[2]、量化控制[3]等方法来减少姿控分系统数传量。近年来事件驱动控制(Event-Triggered Control,ETC)逐渐进入航天器姿态控制学者的视野。目前工程中航天器姿态控制常用定步长的时间触发控制(Periodic Time-Triggered Control,PTTC),然而在状态量变化不大的时刻对控制器更新会占用不必要的通信资源。事件驱动是一种变周期的控制策略,通过设计事件驱动的触发条件,仅在触发条件满足时,控制指令才会更新,能有效减少通信频率,减小总线带宽负载压力。
目前已有的事件驱动在航天器控制方面的研究主要为姿态协同中星间通讯受限问题或者单星稳定控制的研究,而姿态跟踪控制研究较少。文献[4]应用事件驱动的算法,有效解决了编队姿态协同控制飞行中连续通信带来的能源消耗问题。文献[5]给出事件驱动在单个刚体航天器姿态稳定控制中的应用。文献[6]从信息物理融合的角度,研究星上嵌入式系统通讯带宽受限时的姿态控制问题,文中定义的相对负载的概念为航天器控制分系统的通信资源提供了一种评估方法。文献[7]将自适应容错控制与事件驱动结合,能够在容错控制的同时节约通信资源,但针对的是航天器稳定控制任务。
另一方面,由于燃料消耗和星上机构运动等原因,动力学参数不能精确可知,工程中通过参数辨识的方法对不确定惯量参数辨识[8],再根据辨识结果进一步对PID控制器参数进行整定。由于“先辨识再控制[9]”的思路会占用时间资源,因此学者们在传统的PD反馈控制[10]基础上提出了更多智能算法以解决精确惯量未知情况下航天器直接进行姿态控制的问题。文献[11]考虑干扰与模型不确定影响,设计了一种自适应模糊滑模容错控制器,通过对系统广义的干扰实时补偿提高控制精度。文献[12]通过跟踪一个参考模型,设计直接自适应律补偿跟踪误差以抑制模型不确定的影响。文献[13]详细综述了预设性能控制,通过设置性能函数定量描述受控系统的瞬态与稳态性能,可以保证系统状态始终位于性能包络内的高品质控制。文献[14]基于自适应惯量估计器的方法,对惯量矩阵进行估计,仿真表明控制精度显著提高。以上的研究均不考虑通信约束条件,默认为是连续时间的控制器,控制器实时、连续地更新,会对低成本即插即用小卫星网络通信总线带来很大压力。本文将研究含有惯量信息不确定的姿态跟踪控制问题,考虑通信资源约束的条件,将事件驱动控制与惯量自适应估计器结合,设计跟踪控制算法,既减少模型不确定对姿态控制带来的影响,又能减小总线通信负载。
1 数学模型与问题描述
1.1 航天器姿态动力学/运动学误差模型
航天器姿态跟踪误差动力学/运动学模型[10]为
(1)
式中ω∈3表示航天器本体系相对惯性系角速度;ωd∈3表示航天器本体坐标系相对惯性坐标系的期望角速度;ωe=ω-Cωd∈3表示角速度误差;(qv,e,q0,e)∈3×表示误差四元数,qv,e表示误差四元数的矢量部分,q0,e表示误差四元数的标量部分;C表示目标系到本体系的姿态旋转矩阵;J∈3×3表示转动惯量矩阵;u∈3表示三轴控制力矩;d∈3表示三轴干扰力矩。

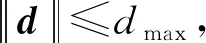
为了便于控制器设计,本文基于如下2个假设:
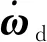
1.2 问题描述
本文的控制目标为式(1)描述的跟踪误差模型,设计控制律使姿态跟踪误差在外干扰力矩作用下仍能收敛至有界区间内。姿态控制问题分为2个内容:1)解决无惯量信息下的姿控问题,2)解决控制系统通信资源约束下的姿控问题。
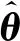

图1 基于事件驱动的自适应姿态跟踪控制系统结构
在事件驱动控制策略下,连续时间的控制被分割为离散的更新时刻,若在一个有限的时间间隔内,事件驱动条件被反复满足,事件驱动间隔趋于0,本应离散的控制变成连续的控制,事件驱动条件失去意义,这种现象在事件驱动研究领域被称为Zeno行为(Zeno behavior)。因此在给出事件驱动条件时,要保证在该条件下,事件驱动的间隔Ti=ti+1-ti存在一个大于0的下界,由此推出在有限时间间隔内,驱动次数不会是无限次。本文将对姿态跟踪所设计的事件驱动条件做出无Zeno行为的分析和证明。
2 事件驱动自适应跟踪控制律
2.1 模型转换
根据文献[5],使用跟踪误差qv,e和ωe定义一种辅助变量s=ωe+βqv,e,β为设计参数。对s求导并代入式(1),则动力学模型转化为
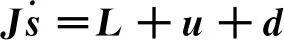
(2)
其中,L为动力学非线性项
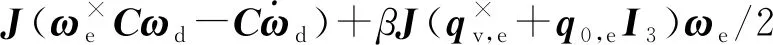
(3)
由于惯量信息未知,需要将转动惯量矩阵参数从L中分离。定义一种矩阵运算F(a)∈3×6
(4)
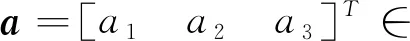
则对任意三维向量a均有Ja=F(a)θ成立。L表示为
L=Yθ
(5)
其中,
Y=-(ωe+Cωd)×F(ωe+Cωd)
(6)
注2. 由式(5)所示,L被分离为2部分,分别为不含惯量信息的Y∈3×6以及θ表示惯量参数。利用该方程,可以设计自适应控制律对θ进行参数估计,从而避免使用惯量真实值。
2.2 事件驱动自适应跟踪控制律设计
设计姿态跟踪控制器为
(7)
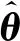
(8)
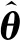
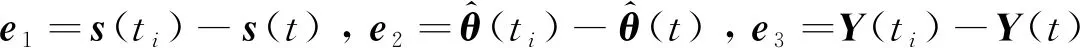
(9)
其中,i=1,2,3,…表示触发时序,0<α<1和γ>0为设计参数。
离了。不离还能过?妮儿啊,你不知道那两年我过的是啥日子,妮儿她娘没有给过我一个好脸。白天在外面还好,一到晚上回来,她就彻底蔫了——就像那院里的合欢,白天精神晚上就收了。她出院回来,我忍着,一直没敢提分开的事,想等她身体恢复恢复再说。没想到,满了月之后她自己倒提了出来。妮儿她爹,拖累你几年了,咱分开吧。说的时候,她也不看我。
注3.α与γ的值越大,采样频率会相应减小,控制精度随之下降。取值时,需要同时考虑通信约束和控制精度要求。γ保证系统始终存在一个小的阈值,避免出现Zeno行为。
2.3 控制系统闭环稳定性证明

|ωe,j|≤2Δ,|qv,ei|≤Δ/β,i=1,2,3
(10)
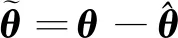
Ω=
证.设Lyapunov函数
求导并代入自适应律(7)得
(11)
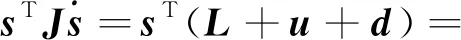
(12)

(13)
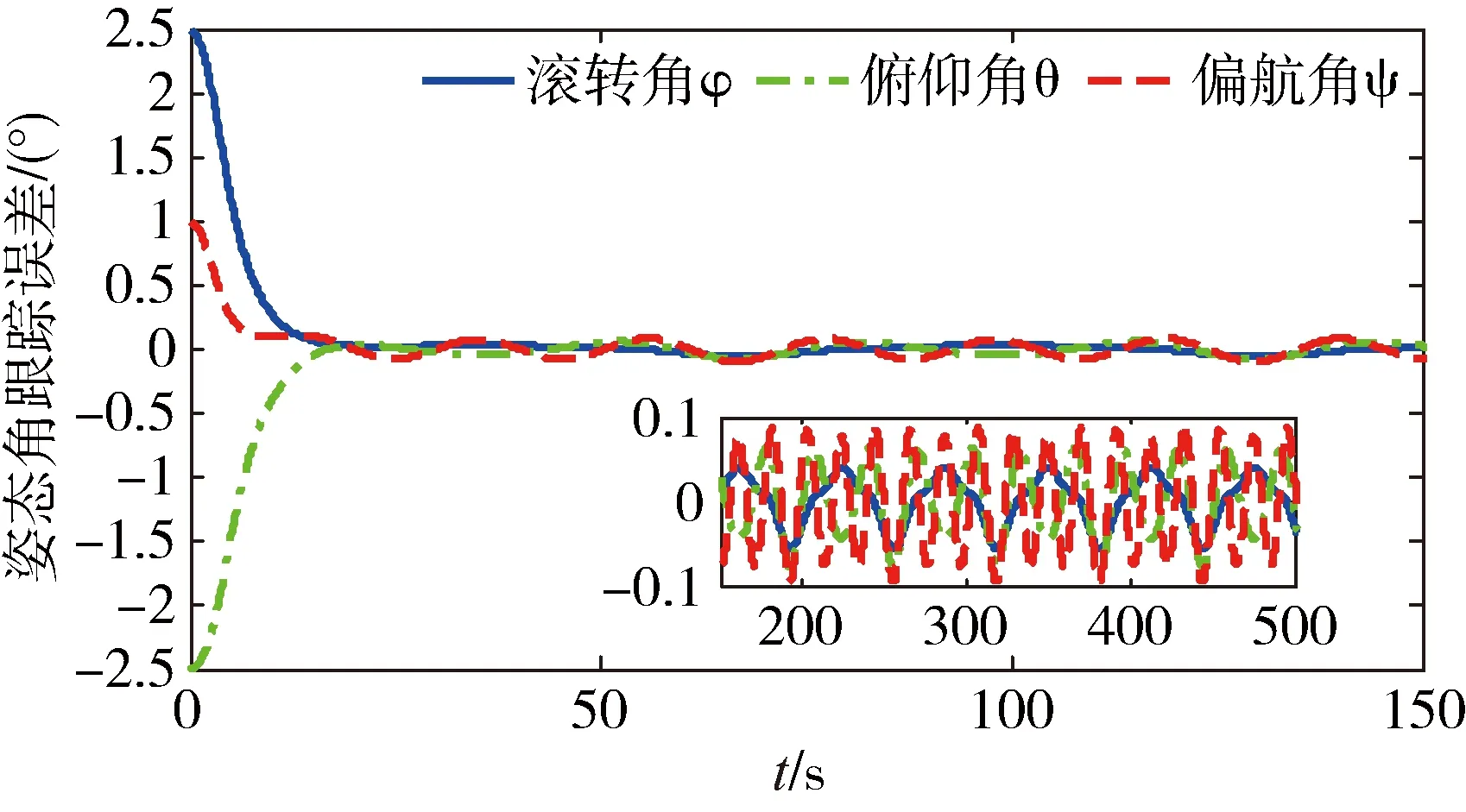
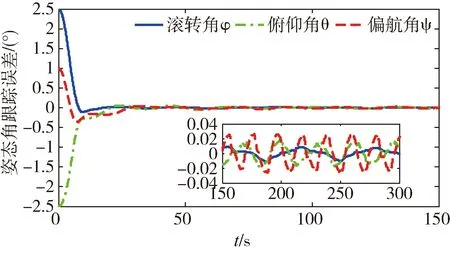
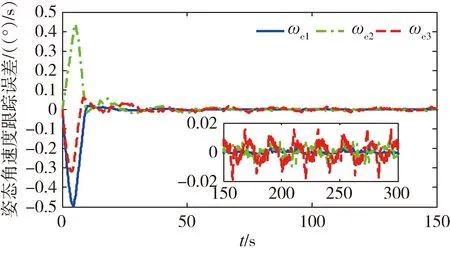
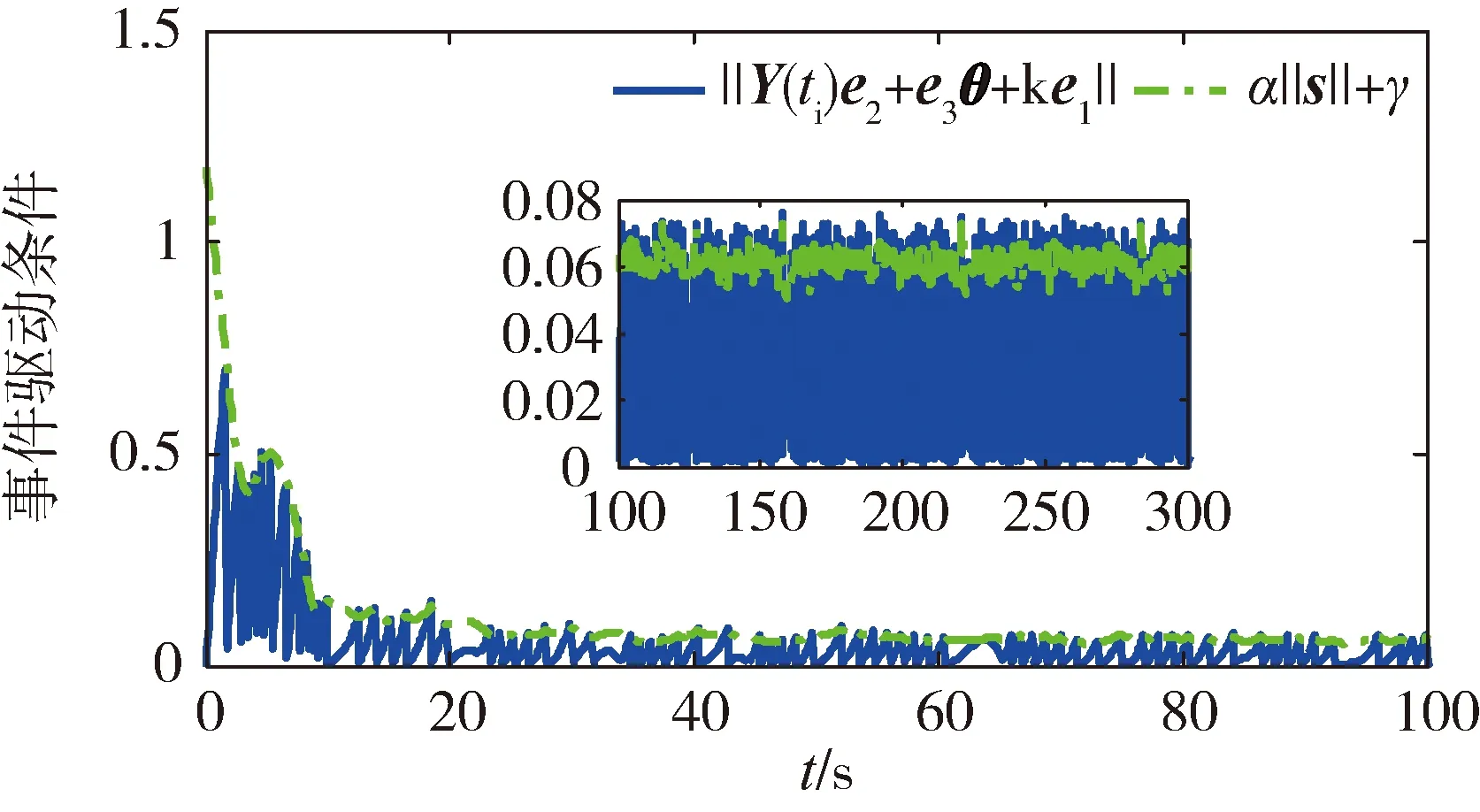
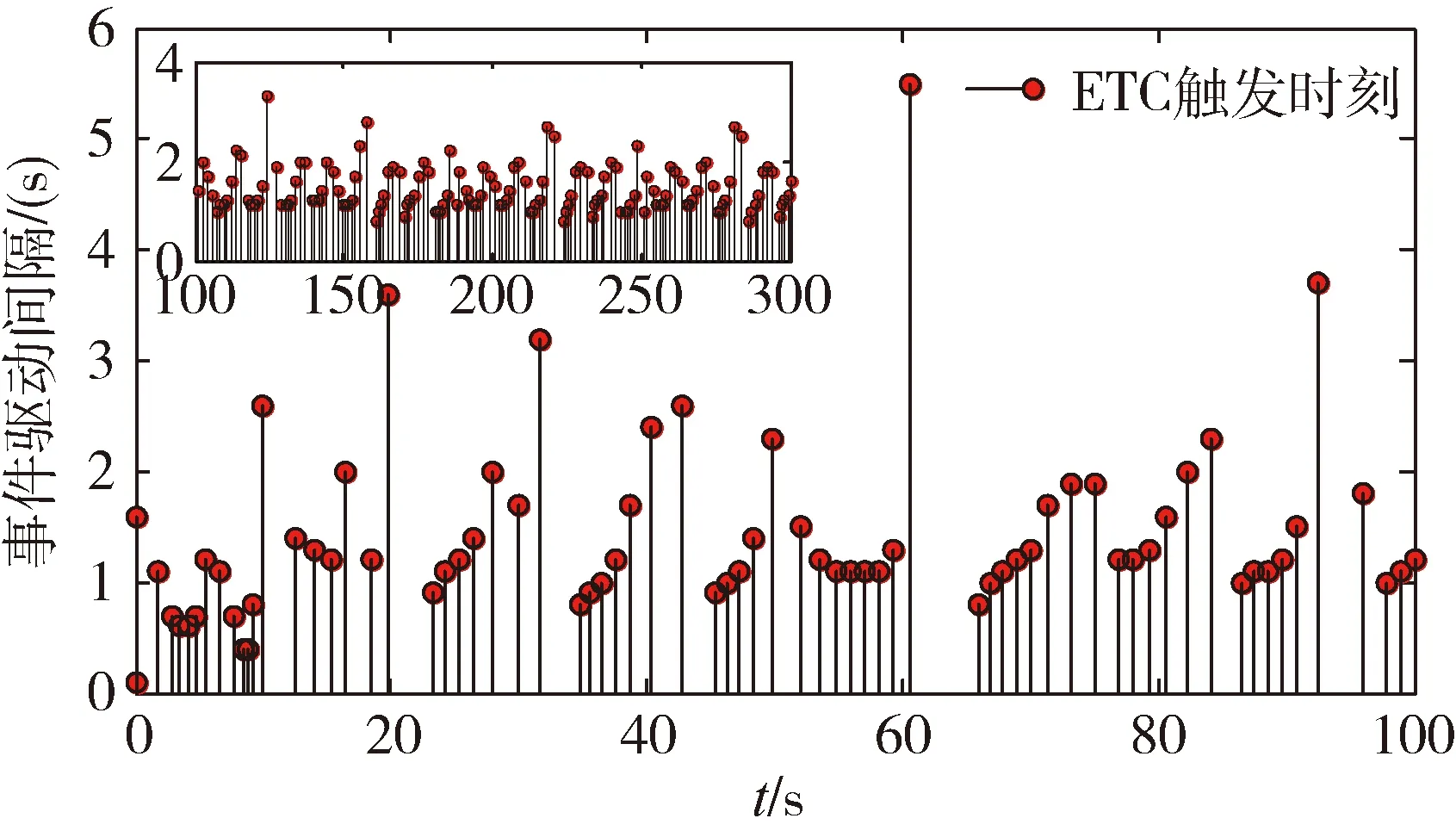
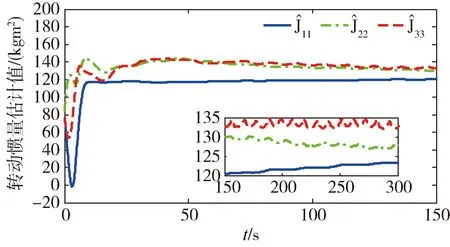
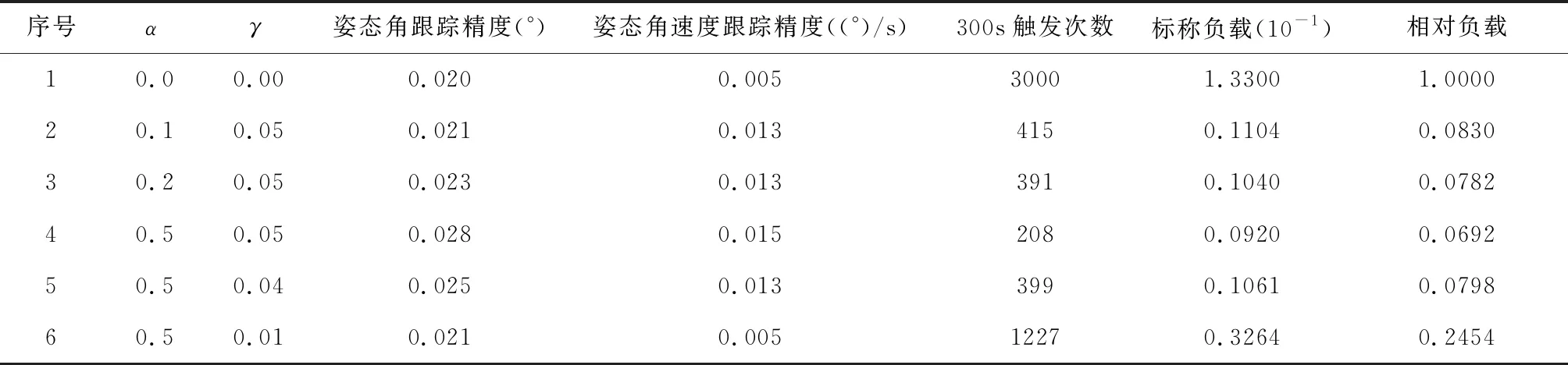
∀μ满足0<μ (14) 其中: ε=2(k-αk-μ)/Jmax 引理[15]2. 对于任意列向量e∈n有成立。 定理2. 在由式(1)描述的航天器姿态跟踪控制系统中,给定期望的跟踪姿态信息满足假设2,则在自适应控制律式(7)((8)和事件驱动触发式(9)作用下,事件驱动更新间隔Ti=ti+1-ti始终存在大于0的下界,无Zeno行为。 (15) 其中,R定义为: (16) (17) 因此两次触发的时间间隔Ti=ti+1-ti可以表示为 (18) (19) 为了例证第2节所设计的控制律和事件驱动触发条件,本节给出姿态跟踪的仿真实例。在转动惯量真实值未知,航天器姿态与期望姿态存在初始偏差情况下,存在2种工况:1)不使用自适应率的PTTC控制。2)使用了自适应率的ETC控制。仿真参数如下: 转动惯量矩阵真实值J与初始估计值J0分别为 J0=diag(80,80,80)kg·m2 故自适应参数的初始估计值为 期望跟踪的角速度为 ωd=[0.005sin(0.1t)0.01sin(0.2t)0.015sin(0.3t)]rad/s 工况1:为了体现本文设计控制律的有效性,作为对照实验,使用类似文献[8]中的PD反馈控制器。控制律为u(t)=-L(J→J0)-kωe-kβqv,e,式中L(J→J0)表示控制器中的非线性项的惯量信息由不精确的惯量代替。控制器的更新间隔为定步长0.1s触发一次的PTTC控制方法。为了使仿真结果更加直观,输出时误差四元数已经转换为欧拉角误差。仿真结果如图2~ 3所示。仿真结果表明,由于控制器中惯量信息为非真实值,影响了控制精度,姿态跟踪精度为0.1°。 图2 工况1姿态角跟踪误差 图3 工况1姿态角速度跟踪误差 图4 工况2姿态角跟踪误差 图5 工况2姿态角速度跟踪误差 图6 工况2控制力矩 图7 工况2事件驱动条件满足情况 图8 工况2事件驱动触发间隔 利用文献[6]提出的一种姿态控制器总线资源使用率的评估方法,评估第3节设计的控制器的通讯资源以及控制精度,以说明注3中的α与γ对控制器性能的影响。 具体方法如下:1)定义一个时间段内总线负载为U=τ/h。其中τ=8a/v,a为数据包大小,单位为bytes,v为总线传输速率,单位为bit/s。2)设计控制周期100ms时的总线负载为标称值U0。其他控制方法中总线负载标称值之比ρ=U/U0为相对负载。ρ越小说明总线负载越低,通信资源节省效果更明显。星上使用的总线传输速率v为19200bit/s,控制输入a数据包为32bytes,传输时间τ为13.3ms,故标称负载U0为0.133。选择不同的事件驱动参数α与γ,仿真结果如表1所示。α与γ的值越大,则触发会相应减小,总线相对负载减小,控制精度随之下降。因此对事件驱动参数取值时要兼顾精度与通信约束。 图9 工况2转动惯量估计值 图10 工况2惯性积估计值 表1 事件驱动参数与跟踪精度及总线负载 针对转动惯量未知的航天器姿态跟踪问题,考虑模块间通讯资源约束,提出了一种基于事件驱动的航天器姿态自适应跟踪算法。该算法能通过自适应率估计惯量真实值,减少模型不准确对姿态控制性能的影响;事件驱动控制策略的引入能大幅度减少通讯频率,减小总线带宽负载,达到节约通信资源的目的。本文给出了控制系统的结构、控制算法设计过程,证明了闭环稳定性,对事件驱动独有的避免Zeno行为作出了证明与分析。通过对照仿真算例表明,该方法可以有效降低模型不确定带来的姿态跟踪误差,减小总线负载。研究内容可为即插即用小卫星姿控设计提供理论参考。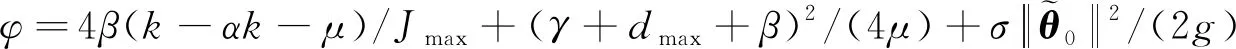
2.4 避免Zeno行为证明


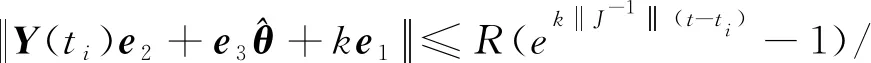
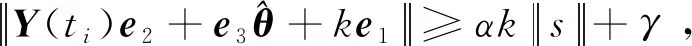

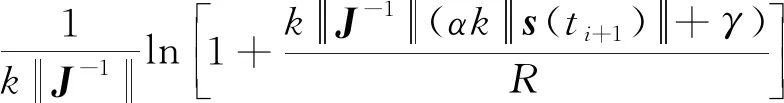

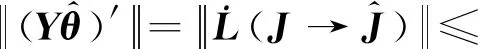
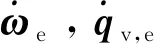
3 仿真校验


4 结论
