基于新息趋势的纳卫星地磁定轨*
2021-04-27陈贵芳
陈贵芳 郁 丰 王 润
1.“空间光电探测与感知”工信部重点实验室,南京 210016 2.南京航空航天大学航天学院,南京 210016
0 引言
作为一种自主的、无长期积累误差且具有较强抗干扰能力的导航技术[1],地磁定轨技术适合对仪器复用率高的纳卫星使用。
当前,地磁定轨多使用批处理算法和卡尔曼滤波算法进行数据融合。前者经多年发展,已有基于无迹变换的批处理算法(unscented batch filter, UBF)提出并应用于地磁定轨中[2]。但批处理算法的数据需提前采集,不适合卫星的实时定位。后者包含扩展卡尔曼滤波器(extended Kalman filter,EKF)和无迹卡尔曼滤波器(unscented Kalman filter,UKF)。EKF引入泰勒近似实现了对非线性系统的状态估计。但地磁模型复杂,求导困难。文献[3-4]建立了多项式拟合的地磁模型,文献[5]则在计算观测矩阵时采用低阶地磁模型,均减小了系统的计算复杂度,但对定位精度提升不多。由于没有忽略高阶项,UKF的精度通常高于EKF。通过引入地平仪[6],太阳敏感器[7-8]等传感器,基于UKF的地磁定轨系统的定位精度可达到千米级。此外,上述传感器也是常用的姿态敏感器,文献[9-10]利用卫星的位置信息估计在惯性系下的地磁矢量信息和地心矢量(或太阳方向矢量)信息,再结合卫星的姿态信息将其转换到卫星本体坐标系下,和传感器的输出值进行比较,实现了卫星的位置和姿态一体化估计。文献[11-12]研究了地磁场幅值和卫星轨道根数在频域上的关系,据此实现了卫星半长轴的高精度估计。文献[13]在此基础上实现了碟状飞行器的姿态估计。
定义磁强计误差和外源磁场扰动为地磁偏差,地磁定轨系统受其影响精度不佳。随科技进步,后者的影响逐渐减小[14]。文献[15]建立了磁强计误差和地理纬度间的函数,在卫星工作时实时补偿地磁信息,减小了定位误差。但磁强计误差还会随着时间而变化,因此该方法不适合卫星长期使用。文献[16]推导并建立了外源磁场的模型并将地磁场模型的系数作为状态向量参与滤波,提升了地磁定轨的精度。但该方法计算量大,不适合纳卫星使用。文献[17]将地磁主磁场模型中构成磁耦极子模型的3个系数作为状态向量参与滤波,仿真证明了该方法的可行性。外源磁场在磁暴时变化剧烈,文献[18]对地磁偏差中的时变部分建模并改进了EKF算法,减小了磁暴下地磁定轨系统的位置误差,但对无磁暴影响时的系统性能提升不大。
本文以地磁场幅值作为观测量,推导了自适应卡尔曼滤波算法(adaptive Kalman filter,AKF),并以此实现了纳卫星的自主导航。该算法将地磁偏差近似建模为随机游走模型并作为状态变量参与滤波。然后,依据新息的变化趋势,实时调整滤波器的参数。以Swarm-A的观测数据的实验表明,该算法有效提升了地磁偏差的估计精度,从而提升了系统的性能。和传统滤波算法对比,AKF的收敛速度更快,其定位精度优于EKF,和UKF相当,最大定位误差约6 km,但计算量却远小于UKF,适合纳卫星等使用。
1 地磁定轨模型建立
1.1 状态方程
以卫星的轨道动力学方程作为系统的状态方程。为简化地磁模型的计算,该方程描述于地心地固坐标系下。由于地磁定轨精度不高,本文只考虑了J2摄动项。
(1)
式中:μ为地球引力常数,Re为地球的参考半径,ω为地球的自转角速度,J2为摄动项系数,f=[fx,fy,fz]为摄动力。
对该方程离散化,得到离散型干扰式:
δXk,k-1=φk,k-1δXk-1,k-1+Γk,k-1Wk-1
(2)

1.2 观测方程
选取国际地磁参考场(international geomagnetic reference field,IGRF)作为地球主磁场模型,其磁位势函数如下:
(3)
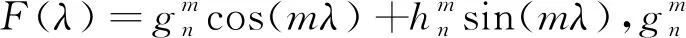
将磁位势对北向、东向和径向求导,则地磁场在北东地坐标系下的分量可表示为:
(4)
选择地磁场幅值作为观测量,观测方程为:
(5)
式中:Bb为地磁偏差,将其建模为随机游走模型,并扩充到状态变量中,η为观测噪声。
(6)
式中:ab为地磁偏差的驱动噪声。
对观测方程离散化,有:
δB=H·δX+η
(7)
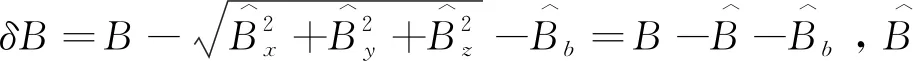
(8)
式中:
地磁模型的高阶导数对轨道修正能力弱[5],为节约星上计算量,该偏微分阵仅考虑地磁模型的低阶项:
(9)
式中:k为低阶截断阶次。
2 自适应滤波算法推导
图1是用Swarm-A卫星在2015年4月19日至20日的实测地磁幅值数据和解算IGRF模型获得的地磁幅值数据做差获得的地磁偏差曲线。由图1可知,地磁偏差随时间和卫星位置的变化而变化,因此常规卡尔曼滤波器的性能会受影响。本文提出了一种自适应滤波算法,依据新息序列的变化趋势,实时调节滤波器的协方差矩阵和状态噪声矩阵,可提升地磁偏差的估计精度,从而提升地磁导航的精度。
定义系统的新息如下:
(10)
式中:Zk为系统观测量。
新息vk的协方差矩阵可由式(11)获得[20]:
(11)
式中:Pk为系统的协方差矩阵,R为系统的噪声矩阵。
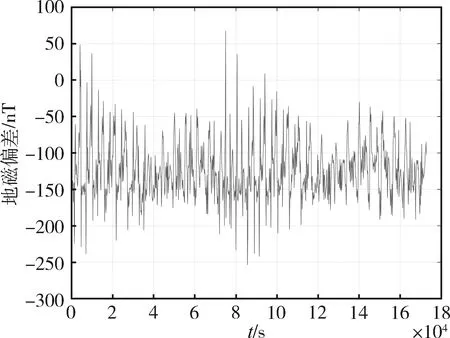
图1 地磁偏差
在系统协方差矩阵时间更新方程中引入变量S(S≥1),有:
(12)
则,
(13)
其中,tr(O)表示求矩阵O的迹。
因S≥1,有:
(14)
新息vk的协方差矩阵可用实际测量的最新N个新息的协方差均值近似表示:
(15)
式中:M为估计窗大小,由经验给定,i0=k-M。
结合式(14)和式(15),有:
(16)
本文认为,若式(16)的右式小于1,则S=1,否则,式(16)取等号。
综上,AKF可表示为:
(17)
3 仿真校验

首先分析各滤波器的定位性能。图2给出了常规滤波器和自适应滤波器的位置误差曲线。地磁场的可观测性弱,滤波器收敛较慢。在0~20000 s间,各滤波器均有不同程度的超调,UKF最大,达到近44 km,AKF最小,仅17 km,并迅速减小到极小值。在系统运行20000 s后,其最大位置误差小于5 km时滤波器收敛。从收敛速度上看,AKF最快,需要约40000 s,而EKF和UKF分别需要50000 s和60000 s才能收敛。从定位精度上看,AKF和UKF的精度最高,而使用EKF的地磁定轨系统的位置误差最大,约10 km。因此,AKF收敛速度最快,精度和UKF相当,最大误差约为6km。
接下来比较各滤波器的计算量。从内存占用上看。UKF通过sigma点集来逼近非线性函数,每次迭代相较于EKF和自适应算法需分别保存2n+1个状态量和观测量的sigma点集(n为状态向量维数),内存需求更大。从运行速度上看。使用一台系统为Windows 10,安装有matlab 2019a的电脑分别以这3种滤波器对同一组数据进行仿真,其仿真时间如表1。可见,UKF的运行速度远低于EKF和AKF。因此,EKF和AKF对计算资源的需求远低于UKF,更适合纳卫星使用。
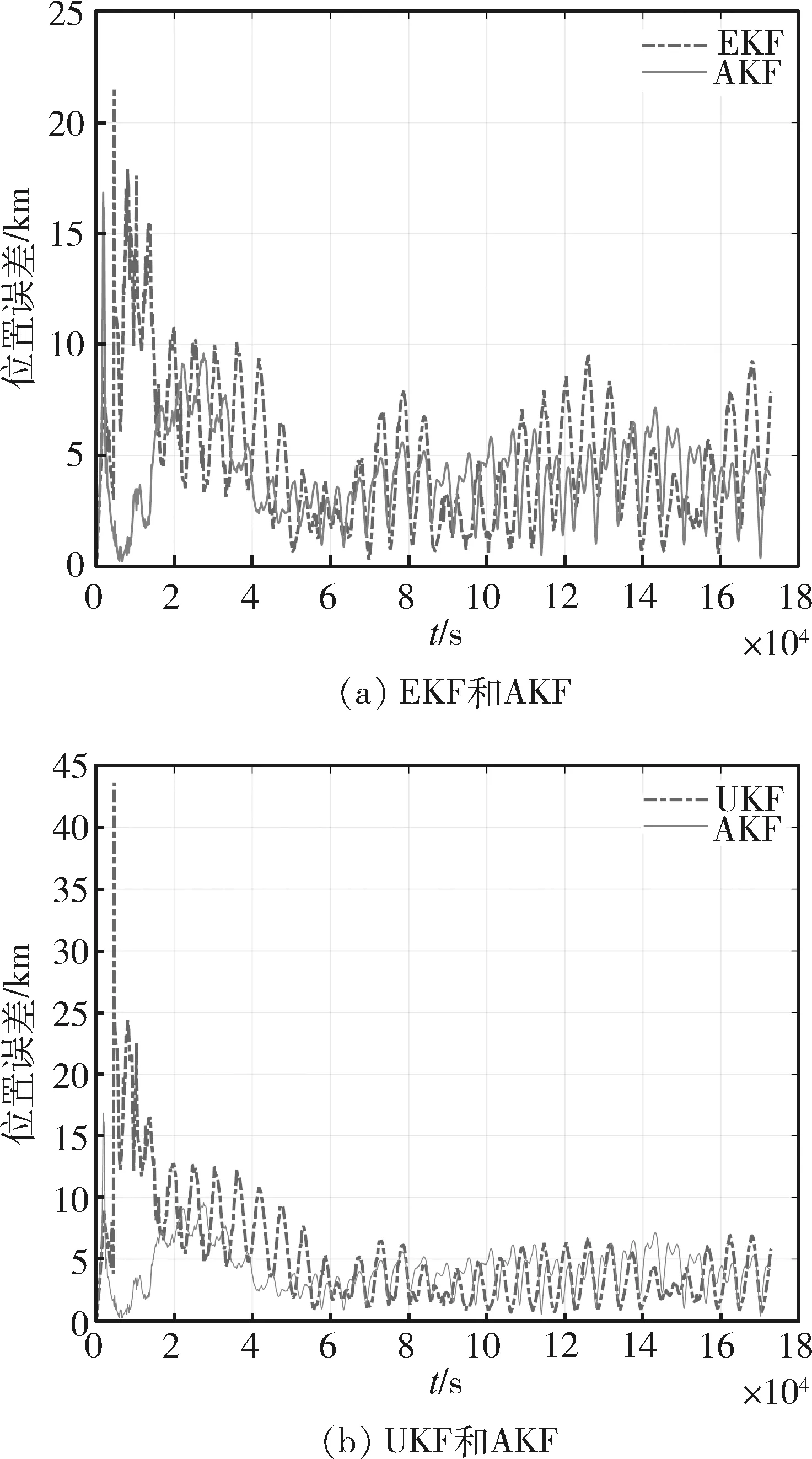
图2 地磁导航位置误差

表1 各滤波器仿真时间
常规滤波器的位置误差曲线有类周期特征。图3给出了地磁定轨系统(EKF)在仅做时间更新时和正常工作时的位置误差曲线。当系统仅做时间更新时,曲线无类周期性,说明该波动与状态方程无关。引入量测修正后,系统的位置误差减小,同时引入了类周期波动。取120000~140000 s的位置误差,在该区间内出现了约3.5个震荡,每次用时约95 min,和Swarm-A的周期相同[22]。由于Swarm-A为极轨卫星,在不同周期,其在地磁场的位置不同。地磁场不同区域的可观测性不同,因此在不同的卫星周期内,其定位性能不一,从而导致了该类周期性波动的出现。
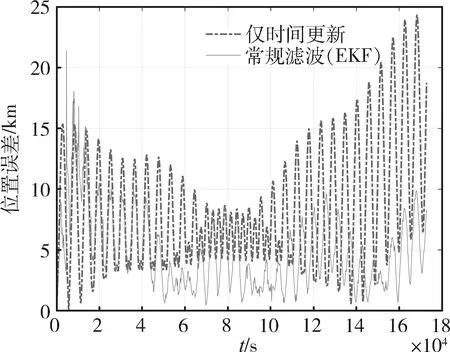
图3 常规滤波(EKF)和仅时间更新的位置误差曲线
最后分析各滤波器对地磁偏差的估计性能。由图4,EKF和UKF的地磁偏差估计曲线近乎重合,说明UKF并不能提升地磁偏差的估计性能。图5是滤波器的地磁偏差的估计误差曲线,这里只比较EKF和AKF。当系统开始工作时,AKF的地磁偏差的估计误差迅速达到一个极小值,在图2(a)表现为位置误差的超调量远小于常规算法。在20000~40000 s之间,AKF的地磁偏差的误差和EKF相近,在位置误差中表现为二者的最大误差接近。40000s后2个滤波器逐步收敛,此后AKF对地磁偏差的估计性能始终优于EKF,其定位误差也更小。因此,本文提出的自适应滤波算法有效地提升了地磁偏差的估计性能,进而提升了地磁定轨的性能。
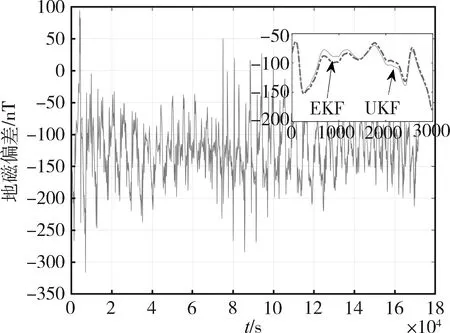
图4 常规滤波器的地磁偏差
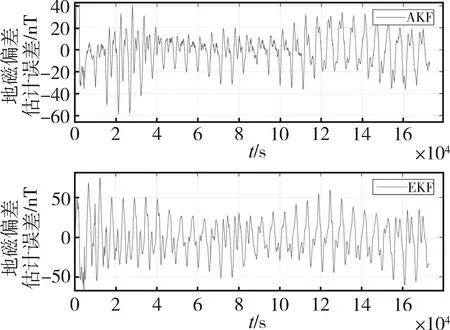
图5 地磁偏差的估计误差
4 结论
对于地磁定轨易受地磁偏差影响的问题,针对性地将其建模为随机游走模型并使之参与滤波。提出了自适应滤波算法,有效克服了空间磁场扰动和磁强计误差的不确定性。实验表明,该算法计算量低,定位精度高,优于传统滤波算法,适合纳卫星使用。
