直线型DELTA并联机器人控制研究

韩治国，陈能祥，许 锦，谢安锋

（1.西北工业大学航天学院，西安 710072；2.深圳前海格致科技有限公司，广东深圳 518052）

0 引言

DELTA并联机器人具有高速、轻载的特点，可通过视觉方案捕捉动态目标，由3个并联的伺服轴确定末端执行器中心的笛卡尔坐标位置，实现对目标的精确定位操作。DELTA并联机器人主要用于各种生产线的上下料、装配、搬运码垛等上下游多种作业，广泛应用于金属加工、工程机械、食品包装、药品分拣、物流装备等领域。DELTA并联机器人以其重量轻、体积小、运动速度快、定位精确、成本低、效率高等特点，已经越来越受欢迎。

DELTA并联机器人根据驱动方式不同主要分为旋转驱动型（旋转型）与直线驱动型（直线型）两种，现在商业化的DELTA并联机器人以旋转型为主，与旋转型相比，直线型DELTA并联机器人具有更大的工作空间和更好的结构刚度，目前对于其运动学分析研究较少。因运动学分析较为复杂，使其控制的实现具有一定的挑战性。

1 直线型DELTA并联机器人建模及仿真

直线型DELTA并联机器人结构如图1所示，其运动主体由3个相同的工业级直线模组（滚珠丝杠传动方式）构成，直线模组以相互间隔120°的角度分别竖直固定在一个圆形平台（也称为静平台）上，直线模组的滑动台上通过球形关节装有两根碳纤维材质的斜拉杆，斜拉杆之间采用弹性连接构成一组定长连杆，由3组连杆驱动一个类6边形的动平台，动平台末端根据实际需要可以安装吸盘或者绘笔等不同类型的执行部件。

图1 直线型DELTA并联机器人实物图

1.1 建模示意图构建

建立机器人的运动学模型是构建运动学性能约束的前提，并联机器人在运动学方面与串联机器人相比呈现明显的对偶特性，串联机器人的运动学正解容易，但逆解较困难，而并联机器人刚好相反，运动学正解很困难，但逆解却非常容易。

直线型DELTA并联机器人建模示意图如图2所示，以静平台中心作为机器人笛卡尔坐标系原点I（0，0，0）、A、B、C 为直线模组基点，H1、H2、H3为直线模组滑动连接点，直线模组只能在一个自由度相对移动，可以直接用移动副AH1、BH2、CH3来表示，移动副垂直静平台运动，并均匀分布在静平台半径为R的圆上，用h1、h2、h3分别表示其运动距离，最大运动距离用H表示。直线模组基点与直线模组滑动连接点位置坐标表示如下：

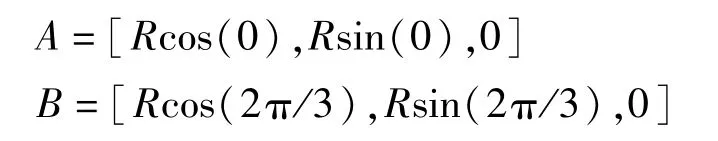
图2 直线型DELTA并联机器人建模示意图

动平台中心用O（x，y，z）表示，其投影在静平台的中心用O′（x，y，z）表示，假设动平台的半径为r，连接动平台的定长连杆分别用H1P1、H2P2、H3P3表示，且有直线型DELTA并联机器人结构实际参数见表1。

表1 直线型DELTA并联机器人结构实际参数

1.2 平行关系证明

为后续建模推导的合理性，必须先证明动平台与静平台是相互平行的。

由图2 可知，MM′∥NN′，PP′∥QQ′，SS′∥TT′，而MM′，PP′，SS′均平行于XY 平面，所以可得NN′∥XY平面，QQ′∥XY平面，TT′∥XY平面。又因为NN′、QQ′、TT′均在动平台平面上，所以动平台平行于XY平面，即直线型DELTA并联机器人在运动过程中动平台与静平台始终平行且不会发生旋转。

1.3 几何约束关系

观察图2，已知OP1始终平行于X轴，从P1点画平行线与AH1相交于A′点，P′1A 为P1A′在静平台投影，构成平面AH1P1P′1，简化后的几何约束关系如图3所示，其中A′H1P1构成一直角三角形，根据勾股定理得：

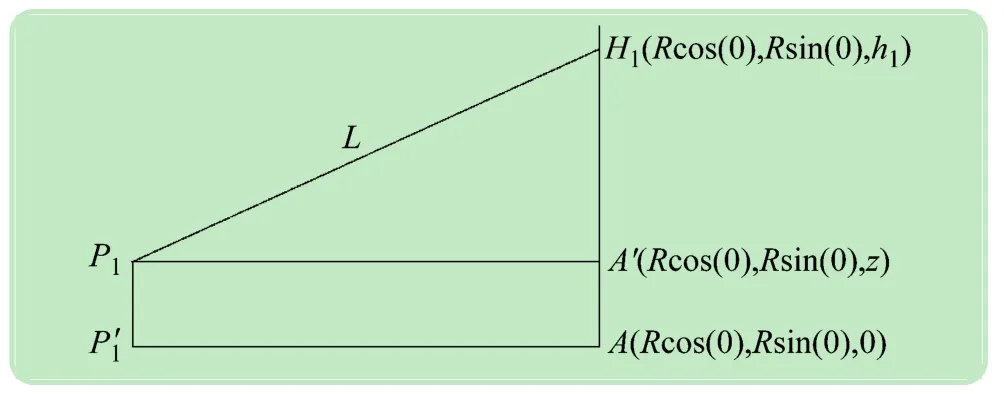
图3 几何约束关系图

同样从P2点画平行线与BH2相交于B′点，P3点画平行线与CH3相交于C′点，同理可得：

1.4 运动学正逆解

联立式（9）～（11）求解方程，在已知h1、h2、h3的条件下求得x、y、z即为该模型下DELTA并联机器人的运动学正解，若是在已知x、y、z条件下求得h1、h2、h3即为该模型下DELTA并联机器人的运动学逆解，由于运动学正逆解求解过程过于烦琐，可以借助Matlab中的solve函数进行求解，参考代码如下：

由于运动学正解结果表达式过长，考虑文章篇幅限制，在此不做具体描述，感兴趣的读者可以参考以上内容在Matlab中自行求解。

1.5 运动学仿真

运动学仿真是机器人学习和研究过程中最重要的步骤之一，它的意义在于可以快速、低成本、高安全性的验证机器人在结构设计、运动学分析以及轨迹规划等方面的有效性。

为了验证上一节运动学分析结果，在仿真中可以规划动平台中心延指定半径圆形轨迹运动，然后观察三组移动副的运动状态，在Matlab中编写三维动态仿真程序，部分代码如下：

编写完成后运行仿真程序，效果如图4所示。

通过观察仿真发现，当动平台中心按规划轨迹运动时，3组移动副运动状态正常，说明了之前对直线型DELTA并联机器人运动学分析的有效性。

图4 运动学三维动态仿真效果图

2 直线型DELTA并联机器人控制程序设计

直线型DELTA并联机器人采用当前机器人主流的通用“个人计算机＋运动控制器”的硬件架构，“个人计算机”端控制程序主要基于C＋＋语言开发，人机交互层采用Qt设计，机器人运动学正逆解函数以动态链接库的形式封装，方便控制程序调用。

根据实际控制功能需求设计控制程序大致流程框图，如图5所示。

图5 控制程序流程框图

根据控制程序流程框图设计完成后的程序运行结果如图6所示。

图6 直线型DELTA并联机器人控制程序

基于C＋＋语言开发的机器人运动学函数库核心源代码参考如下：

运行中的直线型DELTA并联机器人实物如图7所示。

图7 运行中的直线型DELTA并联机器人

3 结语

本文介绍了一种直线型DELTA并联机器人的模型构建与运动控制方法。首先描述了机器人本体的基本结构组成，最大特点就是机械部分采用了模块化设计方式，支持自由拆装，随后对其进行运动学建模，通过3组几何约束关系，求解出运动学正、逆解，并在Matlab环境中进行运动学仿真验证，对仿真结果进行分析。最后使用主流开发语言C＋＋设计运动学函数库，Qt设计控制界面，对机器人进行实时运动轨迹控制，非常直观地感受控制效果。

直线型DELTA并联机器人控制程序源代码采用开源形式，开放性强，用于进行机器人相关实验教学与研究，可以说是比较理想的平台。