基于稀疏堆叠降噪自编码器深层神经网络的语音DOA估计算法

郭业才，侯 坤

（1.南京信息工程大学电子与信息工程学院，南京 210044；2.江苏省大气环境与装备技术协同创新中心，南京 210044；3.南京信息工程大学滨江学院，江苏无锡 214105）

0 引言

波达方位（Direction of Arrival，DOA）估计是通过信号的空间特征参数，确定信号在空间域中的位置信息，如距离、方位角、俯仰角等［1-6］。声源定位技术是波达方位估计的一种重要手段，其中多重信号分类（Multiple Signal Classification，MUSIC）算法［7］和旋转不变性子空间（Estimating Signal Parameter Via Rotational Invariance Techniques，ESPRIT）算法［8］是传统的DOA技术。它们在低信噪比环境下定位误差大。随着计算机技术的发展和智能算法的出现，声源定位技术得到了发展。文献［9］中提出基于局部保持投影和径向基（Radial Basis Function，RBF）神经网络的DOA估计算法，利用局部保持投影对神经网络的训练样本进行降维，加快了神经网络的训练过程，但定位精度不高；文献［10］中提出从广义互相关（Generalized Cross Correlation，GCC）向量中提取方位特征送入多层感知器（Multi-layerperceptron，MLP）网络学习的DOA估计算法定位准确，但抗噪性较差。

1 DOA 估计模型［11-12］

假设空间中有M个阵元组成的线性均匀阵列，窄带声源信号为θi（i∈［1，2，…，k］），每个信号源互不相干的入射到麦克风阵列上，第m个麦克风接收的信号为

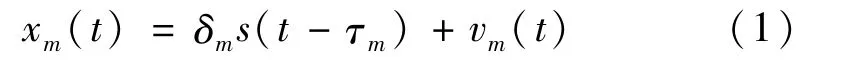
式中：m ＝1，2，…，M；δm为第m个阵元对信号的增益；s（t）为t时刻声源入射信号；τm为第m个阵元接收声源信号相对于参考阵元的时延；vm（t）为t时刻第m个阵元的噪声。式（1）的矩阵形式为

式中：A为信号的导向向量。假设噪声均值为0、方差为σ2的高斯白噪声，则麦克风阵列接收信号的协方差矩阵为

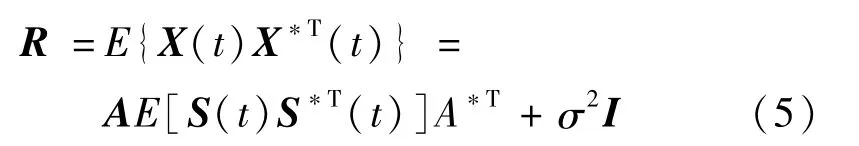
式中：*表示共轭。R的矩阵形式为

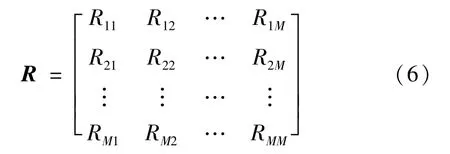
将协方差矩阵R的上三角阵中元素的实部、虚部分开后作为SSDAE-DNN的输入，即

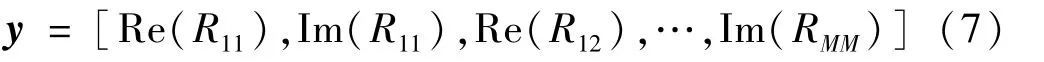
式中：Re（·）为取实部；Im（·）为取虚部。

2 SSDAE-DNN网络框架

本文网络框架由SSDAE与DNN网络组成，如图1所示。通过SSDAE网络进行抗噪训练，将训练得到的最优权重迁移给DNN网络作为输出训练权重，通过损失函数优化DNN网络模型，建立语音信号特征yn和方位角θ之间的非线性映射关系。将语音DOA估计问题视作分类问题，通过SSDAE-DNN网络对yn进行分类，根据分类结果选取对应的角度标签，实现对方位角θ的估计。

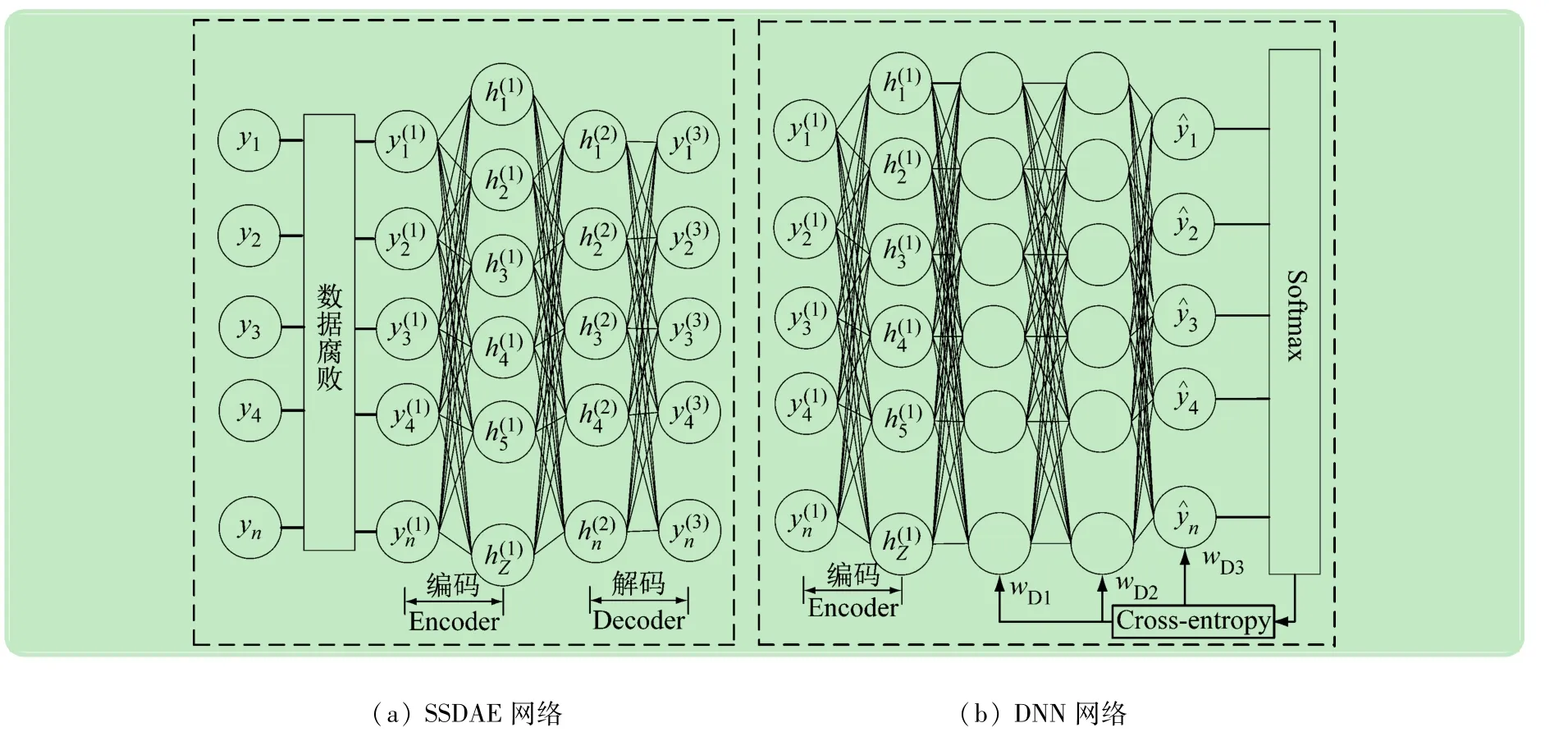
图1 SSDAE-DNN网络结构

2.1 堆叠稀疏自编码器

文献［13-15］中提出的去噪自编码器（De-noising Self Encoder，DAE），由输入层、隐藏层和输出层组成。在DAE的损失函数中加入稀疏因子ρ就构成稀疏去噪自编码器（Sparse De-noising Self-encoder，SDAE）。SDAE同时具有稀疏性和鲁棒性，网络结构如图2所示。

日前，在美国举行的世界啤酒品评大赛“世界啤酒锦标赛”中，青岛黑啤以出色的口味与品质征服评委味蕾，一路“过关斩将”夺得金奖。无独有偶，11月14日，“2018欧洲啤酒之星”大赛颁奖仪式在德国南部城市纽伦堡会展中心举行，青岛啤酒皮尔森从来自全球51个国家、2344款啤酒产品中脱颖而出，荣获“欧洲啤酒之星”大奖。

图2 SDAE算法流程图

预处理过的训练样本yn分配给输入层，隐藏层单元为

式中：Z为隐藏层单元数；W∈RM×N为编码器权重矩阵；be为编码偏置。输出层单元为：

式中：f（·）为非线性激活函数；WT∈RM×N为解码器权重；bd为解码偏置。SDAE网络的损失函数为

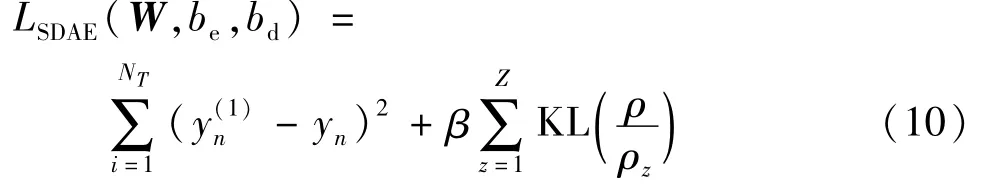
式中：NT为数据集数量；β为超参数，其值在训练过程中通过调整最优参数时决定；KL为Kullback-Leibler散度；ρz为第z个隐藏单元的平均激活度，且

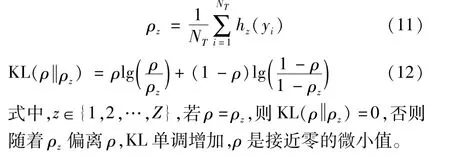
SSDAE网络由多个SDAE堆叠而成，前一个SDAE隐藏层的输出作为下一个SDAE的输入，网络结构如图3示。

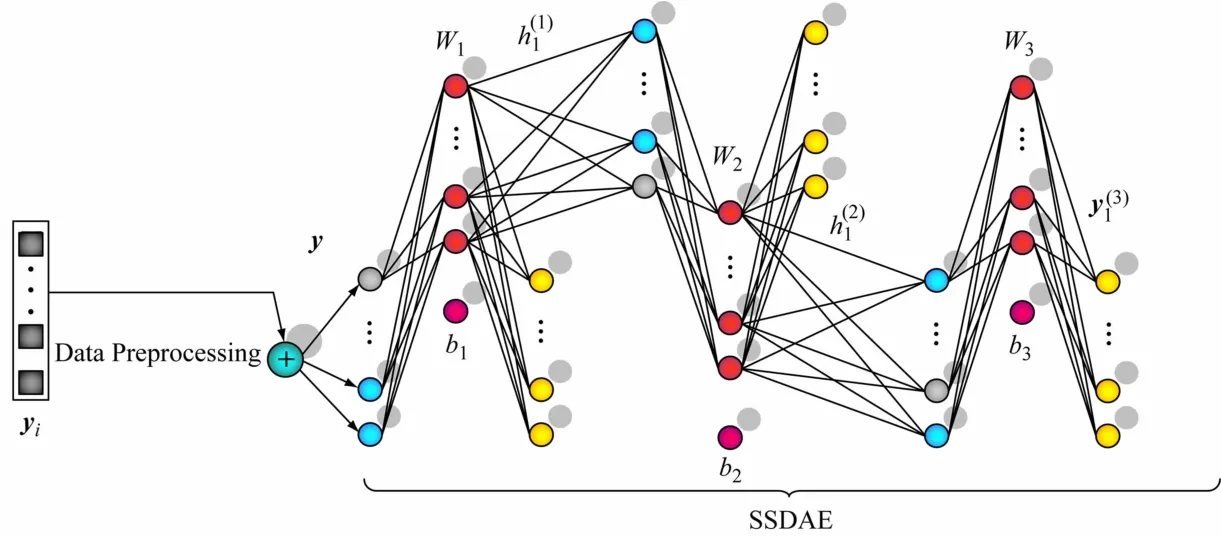
图3 SSDAE网络结构

SSDAE网络采用贪婪逐层进行训练，单独训练每一个SDAE网络得到最优权值后作为SSDAE网络的初始权值，通过反向传播（BP）整体微调，直至得到最优参数，微调阶段的损失函数为与式（10）相比，式（13）无稀疏约束项，是由于训练单个SDAE时已包括稀疏约束。

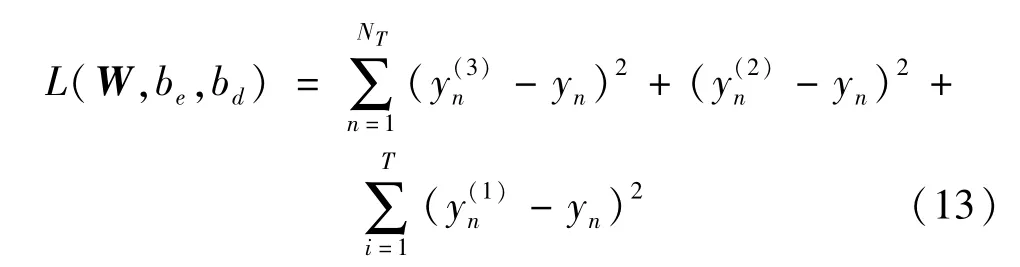
用SSDAE网络对语音定位进行预训练时，添加了抗噪训练，优化了特征选择，稀疏因子ρ将包含无用信息的特征权重置为0，降低了训练复杂度，提升了算法的抗噪性能与收敛速度，且可从有限的样本中提取到更多的特征信息。

2.2 DNN网络框架

本文采用的DNN网络如图1（b）所示，有3层全连接隐藏层。将SSDAE网络预训练模型的最优权值作为DNN的初始权值，减少了DNN网络模型的训练时间。同时，因SSDAE网络在编码过程中加入了高斯白噪声进行抗噪训练，采取迁移策略迁移权重后，一定程度上提升了DNN网络的抗噪性能。通过3层全连接隐藏层强化特征提取和非线性映射能力，建立DNN学习特征与DOA估计之间的非线性映射关系，获得一个抗噪性强的稳健DOA估计系统。隐藏层为

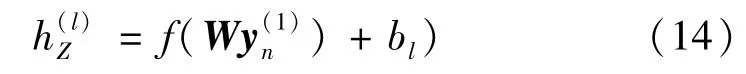
式中，l为隐藏层的层数，l∈｛1，2，3｝。

DNN网络框架的损失函数为

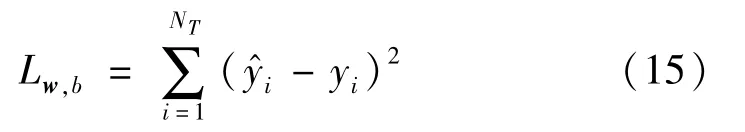
2.3 性能评价指标

以均方根误差（Root Mean Square Error，RMSE）作为算法性能评价指标，比较本文算法、基于多层感知器（Multilayerperceptron，MLP）、径向基函数（Radial Basis Function，RBF）和MUSIC的DOA估计算法的准确性和稳定性。RMSE定义为

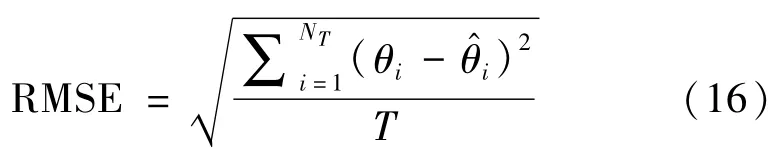
式中，θi、分别为真实值与估计值。

3 算法仿真

3.1 仿真条件

房间尺寸为5.5 m ×3.3 m ×2.3 m，麦克风阵列阵元间距为5 cm，第一个阵元为参考阵元，声源与麦克风相距1.5 m，均匀阵列的高度为1.2 m，如图4所示。房间内墙面（普通石灰墙）的反射系数为0.95，地板的反射系数为0.90，麦克风阵元个数为8。

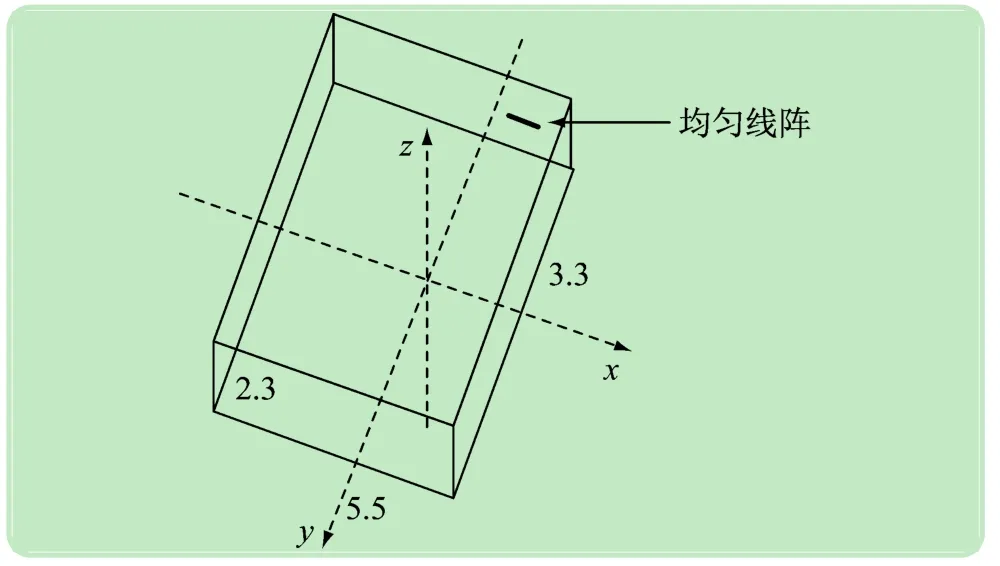
图4 仿真条件示意图（m）

数据集声源信号取为纯净语音信号，入射角度为0.1°，信号遍历各个分组的定位范围，按8∶2的比例随机抽取制作训练集和数据集，数据集规模约为3.6×104个。将音响放置在参考阵元的四周作为声源，实验数据由一个8阵元线性麦克风阵列采集。

3.2 迭代时间对比

以基于SSDAE-DNN、MLP和RBF神经网络的DOA估计算法为互比对象，分别使用4 500、9 000和18 000个训练样本。3种算法的运行时间见表1。表1表明，基于SSDAE-DNN和MLP网络的DOA估计算法的运行速度远远快于基于RBFNN网络的DOA估计算法，而本文算法的运行速度又快于基于MLP网络的DOA算法。

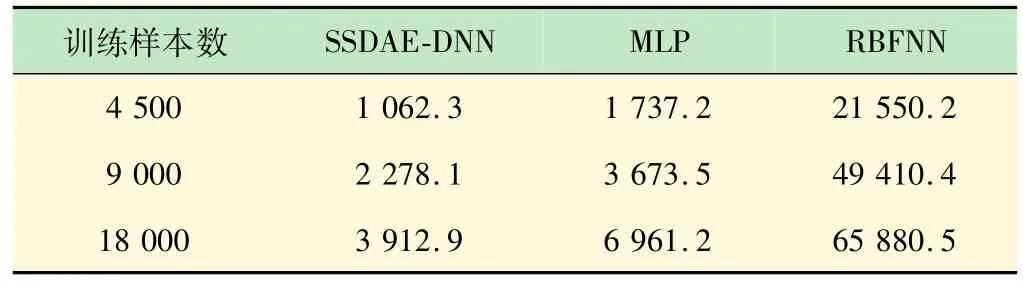
表1 3种算法的运行时间 s

3.3 信噪比对系统性能的影响

在不同信噪比下，比较基于SSDAE-DNN、MUSIC、MLP和RBFNN的DOA估计算法的抗噪性能。信噪比范围为－5～15 dB，其余仿真条件与前面相同。图5表明，3种DOA估计算法的RMSE均随信噪比增大而逐渐减小，而本文算法的RMSE均小于其他算法，有更好的精确性和抗噪性。

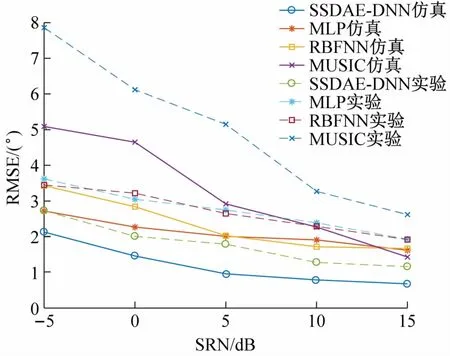
图5 信噪比对系统性能的影响

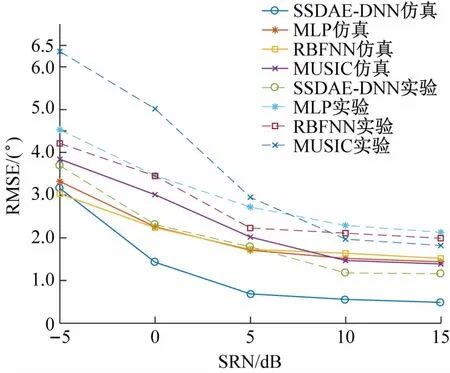
图6 阵元数对系统性能的影响

3.4 阵元数对系统性能的影响

在不同阵元数下，比较基于SSDAE-DNN、MUSIC、MLP和RBFNN的DOA估计算法的RMSE。麦克风阵元个数分别为4、6、8、10和12，其余仿真条件与前面相同。图6表明，3种算法的RMSE均随阵元个数及输入网络特征个数增加而逐渐降低且变化也趋于平缓，而本文算法的RMSE在4个阵元时大于基于RBF的DOA估计算法，但随着阵元个数的增加，RMSE逐渐减小且小于其他算法。

4 结语

针对低信噪比时传统的DOA估计算法定位误差大问题，提出了基于SSDAE-DNN神经网络的语音DOA估计算法。该算法通过SSDAE增强了网络框架的抗噪性能，通过迁移学习转移权重提升了DNN网络框架的泛化性。仿真与实验结果表明，在低信噪比下，本文算法的性能上优于基于MLP、RBF和MUSIC的DOA估计算法。