一类Van der Pol-Duffing系统的变结构滑模控制
2021-04-27李德奎张怀德
李德奎, 张怀德
( 甘肃中医药大学(定西校区) 理科教学部,甘肃 定西 743000 )
0 引言
混沌运动是非线性系统在特定条件下独有的一种运动形式.近年来,许多学者对Duffing系统[1]和Van der Pol系统[2]进行了广泛研究,并提出了Van der Pol-Duffing系统.由于Van der Pol-Duffing系统中既含有Van der Pol系统维持自激振荡的非线性阻尼项,又含有Duffing系统的3次非线性恢复力项,因此它具有非常丰富的动力学特性[3-6].目前,对Van der Pol-Duffing系统的研究主要集中在其动力学性质方面,如混沌与分岔、微弱信号检测、稳态响应等.文献[7]提出了一类含有平方项和5次幂项的Van der Pol-Duffing系统,并应用多尺度法研究了该系统的Hopf分岔控制问题,但未能对该系统的混沌控制问题进行深入研究.混沌控制与同步是混沌研究和应用的两个重要方面,其相关研究已取得较多成果,如参数微扰法(OGY方法)[8-9]、时滞反馈控制法[10]、自适应控制法[11]、滑模控制法[12-13]等.滑模变结构控制法是通过对控制器进行来回切换将系统控制到预定的状态,因此该系统具有很强的鲁棒性.基于以上研究,本文研究一类含有平方项和5次幂项的Van der Pol-Duffing系统的滑模变结构控制问题,并在系统参数已知和未知的两种情况下分别通过构造有效的变结构滑模控制器,将该系统控制到预期的运动状态.
1 模型的描述
Van der Pol-Duffing系统的一般方程为
(1)
式中:x为系统的状态变量,μ为阻尼系数,a和b分别为线性和非线性刚性系数,f为外力激励的振幅,ω为外力激励的频率,φ为外力激励的初相.系统(1)具有线性项和非线性3次幂项.
文献[7]给出了一类改进的Van der Pol-Duffing系统,该系统同时含有平方项和5次幂项,其动力学方程为
(2)
其中ai(i=1,2,3,4)和b为系统参数,其余字母的含义与系统(1)中的相同字母所表示的意义相同.与系统(1)相比可知,系统(2)增加了两个高次项,因此系统(2)的动力学行为更加复杂.
系统(2)可进一步写成如下形式的微分方程组:
(3)
采用Runge-Kutta方法对系统(3)进行数值仿真,参数取a1=-1.5,a2=3,a3=1.2,a4=2.5,f=6,ω=2,φ=0,初值条件为x(0)=0.5,y(0)=0.3.系统(3)的状态变量x随参数b变化的分岔图如图1所示.从图1可以看出,在其他参数一定的情况下,随着参数b的变化系统出现了周期运动、倍周期分岔、混沌等现象,由此表明系统具有非常复杂的动力学行为.从图1还可以看出,当参数b=-1时,系统处于混沌状态.当参数b=-1时,系统(3)的Lyapunov指数谱如图2所示.从图2可以看出,当参数b=-1时,系统(3)有一个Lyapunov指数(λ1=1.239 3)大于0,这说明在给定的参数条件下系统(3)处于混沌运动状态,并具有如图3所示的混沌吸引子相图.
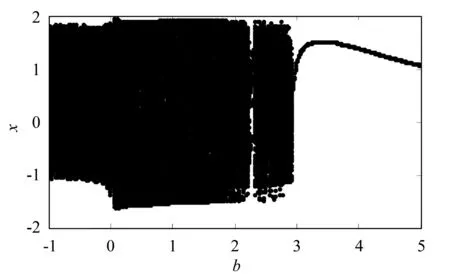
图1 状态变量x随参数b变化的分岔图
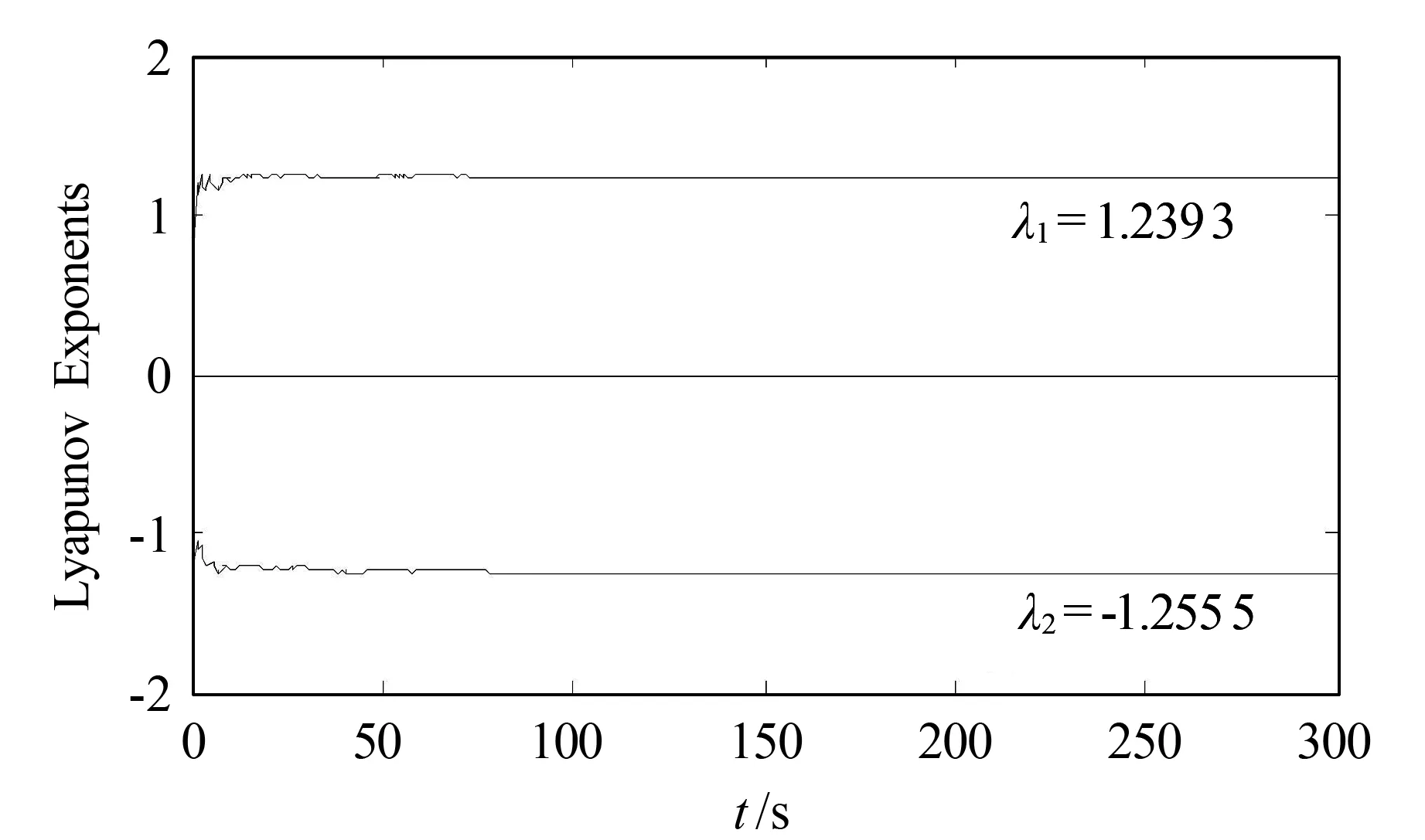
图2 系统(3)的Lyapunov指数谱
2 系统参数已知的滑模变结构控制
描述参数已知的受控Van der Pol-Duffing系统的方程为:
(4)
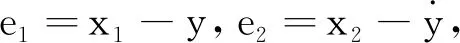
(5)
为了使误差系统(5)的零解是渐近稳定的,需要对系统(4)进行滑模控制,为此选取的滑模面为
τ=ke1+e2,
(6)
式中k>0.根据霍尔维茨定理可知,式(6)是渐近稳定的.
为了实现系统(4)的运动状态能在有限时间内到达并稳定于式(6),需构造有效的滑模控制器.首先选取Lyapunov函数V=τ2,显然V>0.对Lyapunov函数沿式(5)对时间t求导可得
(7)
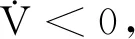
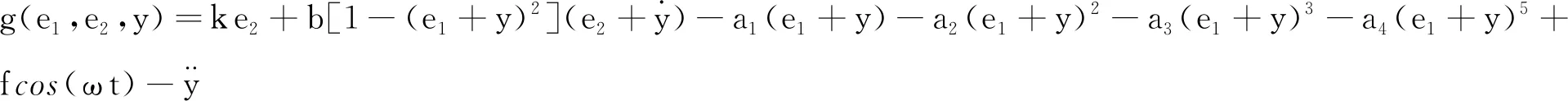
(8)
定理1若选取变结构滑模控制器(8),则误差系统(5)能够在有限时间内到达并稳定于式(6),即混沌系统(4)能够在有限时间内稳定跟踪到信号y.
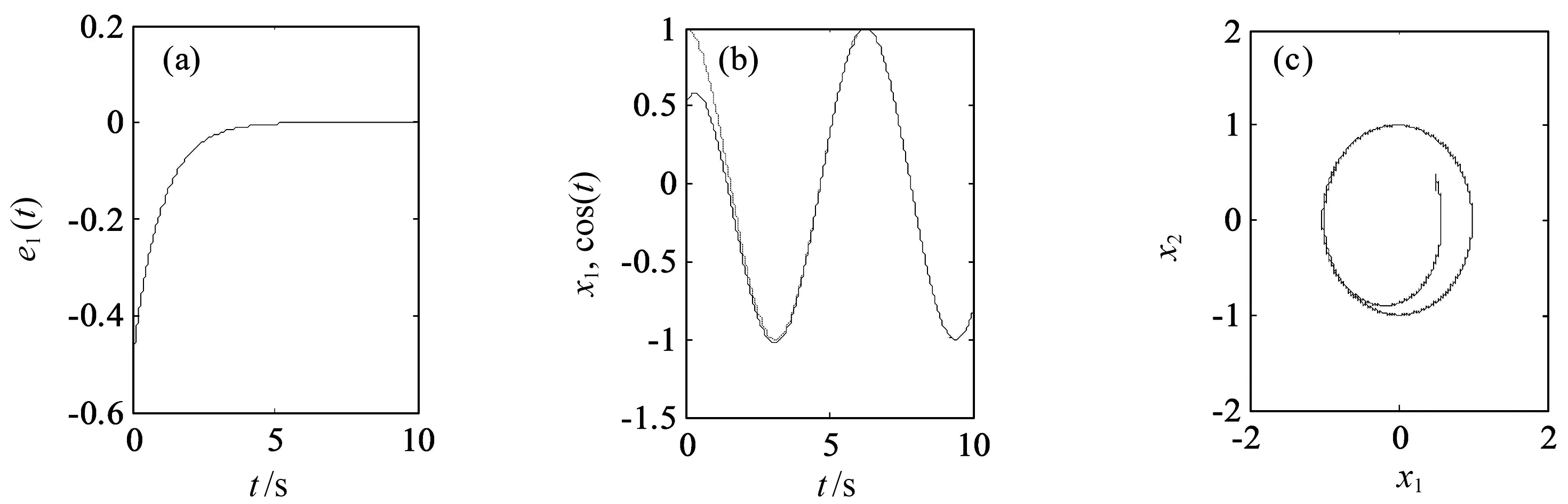
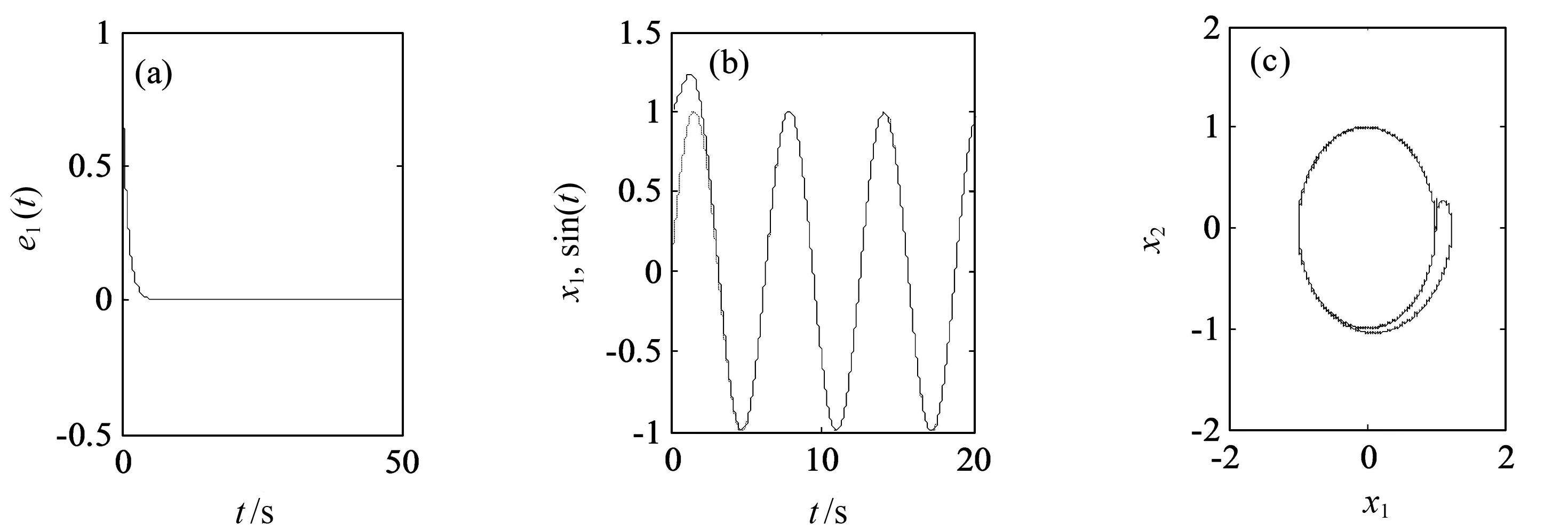
下面利用数值仿真验证定理1的正确性.任意选取二阶可导的连续有界信号y=cost,取k=1,其余参数已知,初值条件为x1(0)=0.5,x2(0)=0.3.由l1 从图5可以看出,滑模变结构控制器(8)对系统(4)的跟踪控制效果较为理想.其中:图5(a)中的误差曲线快速趋向于零刻度线,说明状态变量曲线快速趋向目标曲线;图5(b)中的状态曲线x1能够快速追踪目标曲线cost,说明所构造的变结构滑模控制器(8)能够对系统(4)进行有效控制.根据误差的定义,当e1=x1-cost→0,e2=x2+sint→0时,x1→cost,x2→-sint,这说明滑模控制器(8)将图3所示的混沌曲线控制到了单位圆上(如图5(c)所示). 在数值仿真中,l2和l1也可分别取函数g(e1,e2,y)的任意上、下界,并且l2和l1取值的绝对值越大,混沌系统(4)稳定跟踪到预设信号的时间越短.因此,只要l2和l1取较大的绝对值就可使混沌系统(4)跟踪到预设信号,从而使控制器的选取变得更加简单. 图3 系统(3)的混沌吸引子相图 图4 函数g(e1,e2,y)随时间变化的序列图 (a)系统(4)的误差曲线 (b)系统(4)的状态变量曲线 (c)系统(4)的相图图5 滑模控制器(8)对系统(4)的控制效果 描述参数未知的受控Van der Pol-Duffing系统的方程为: (9) (10) 为了使误差系统(5)的零解是渐近稳定的,需对其进行滑模控制,为此选取的滑模面为 τ=e1+e2. (11) (12) (13) 将式(13)代入式(12)中可得 定理2若选取自适应变结构滑模控制器和未知参数辨识法则(13),则误差系统(10)能够在有限时间内到达并稳定于式(11),即混沌系统(9)能够在有限时间内稳定跟踪到信号y. 下面利用数值仿真验证定理2的正确性.任意选取二阶可导的连续有界信号y=sint,初值条件取x1(0)=0.5,x2(0)=0.3,固有参数值为a1=-1.5,a2=3,a3=1.2,a4=2.5,f=6,ω=2,φ=0.由式(13)可知,对系统(9)施加的自适应变结构控制器以及未知参数的辨识法则可分别表示为: sint-6sgn(x1+x2-sint-cost); (14) (15) 对系统(9)施加自适应变结构滑模控制器(14)后得到的对信号y=sint的跟踪效果如图6所示.从图6可以看出,自适应滑模控制器(14)对系统(9)的跟踪控制效果较为理想.其中:图6(a)中的误差曲线快速稳定于零刻度线,说明状态变量曲线快速趋向目标曲线;图6(b)中的状态变量曲线x1快速追踪到目标曲线sint,说明所构造的自适应滑模控制器(14)能够对系统(9)进行有效的控制.根据误差的定义,当e1=x1-sint→0,e2=x2-cost→0时,x1→sint,x2→cost,说明自适应滑模控制器(14)将图3所示的混沌曲线控制到了单位圆上,如图6(c)所示. (a)系统(9)的误差曲线 (b)系统(9)的状态变量曲线 (c)系统(9)的相图图6 自适应滑模控制器(14)对系统(9)的控制效果 本文基于Lyapunov指数理论和分岔理论对一类含有平方项和5次幂项的Van der Pol-Duffing系统进行研究发现,该系统具有非常复杂的动力学行为(包括周期运动、倍周期分岔、混沌运动等).通过构造两类简单的变结构滑模控制器对该系统的混沌行为进行跟踪控制发现,该系统在参数已知和未知两种情况下均能够被跟踪控制到预期的运动状态.研究还表明,在系统参数已知的情况下,该系统的变结构滑模控制器的选取非常简单,只要l2和l1取绝对值较大的数值就可使该系统能够跟踪到预设的信号,且绝对值越大,控制所需的时间越短.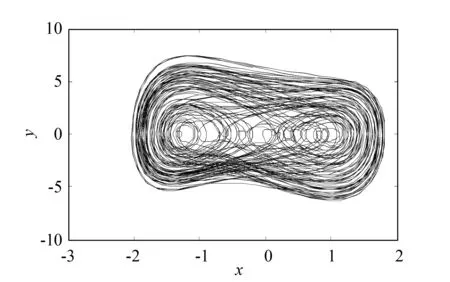

3 参数未知系统的变结构滑模控制
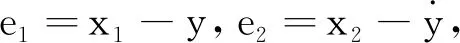
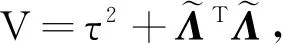


4 结论
