皮革裁剪路径优化算法的研究
2021-04-27汪岚陈海洋
汪岚, 陈海洋
( 黎明职业大学 智能制造工程学院,福建 泉州 362000 )
我国是皮革生产、消费大国.裁剪作为皮革加工中的关键工序,对整个皮革加工效率具有重要影响.目前,国内企业使用的数控皮革裁剪机其生成的裁剪路径基本都是通用型,这使得裁剪过程不仅运动轨迹复杂,而且裁刀在样片之间移动时会不可避免地生成大量的空行程,增加走刀时间.因此,面对数量众多、轮廓各异的待裁样片,如何规划一条科学合理的裁剪路径对提高生产效率和增强企业的市场竞争力具有重要意义.通常,裁剪路径优化问题被归结为广义旅行商问题(GTSP)[1],并且已有很多学者利用遗传算法[2-4]、蚁群算法[5-6]、局部搜索算法[7]等对其进行了优化求解.但在实际应用中发现:采用单一算法优化裁剪路径时,其优化能力难以求解GTSP这一复杂问题;采用局部搜索算法优化裁剪路径时,容易丢失最优解空间;采用多种智能算法相结合的混合算法优化裁剪路径时,因复杂度较大而耗时过长.因此,本文提出一种分类优化算法,在保留最优裁剪路径解空间的前提下,实现GTSP向TSP(旅行商问题)的转化,以此降低算法求解的复杂度,实现皮革裁剪最优路径的快速求解.
1 裁剪路径优化模型
1.1 裁剪路径问题的描述
数控皮革裁剪机的裁剪路径为:裁刀由原点出发,行走一段空行程后达到第1块待裁皮革样片的裁剪起始点;入刀后按照设定方向沿样片轮廓路径进行裁剪,裁剪完毕后回到该样片的裁剪起始点出刀.以此类推,继续行走一段空行程后移动到第2块待裁剪皮革样片的裁剪起始点进行裁剪加工.重复上述步骤,待完成所有样片的裁剪加工后,裁刀回到原点.故裁刀裁剪路径的数学模型可表示为:
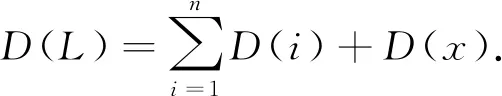
(1)
1.2 空行程路径优化模型
由于裁刀空行程路径问题可视为一个广义旅行商问题,因此根据图论[8]可将其描述为:假设G=(V,A)是一个赋权有向图,其中V={V1,V2,…,Vn}是G的n块样片的顶点集合,A={(vi,vj):i≠j,vi≠vj,vi,vj∈V}是G的边集或弧集.各样片的顶点集合分别为V1={v1,1,v1,2,…,v1,V(1)},V2={v2,1,v2,2,…,v2,V(2)},…,Vi={vi,1,vi,2,…,vi,V(i)},…,Vn={vn,1,vn,2,…,vn,V(n)},其中V(i)为第i块样片的顶点数,V=V1∪V2∪…∪Vn,Vi∩Vj=Ø (i≠j).
由上述可知,裁剪空行程路径优化问题就是在赋权有向图G中寻找一条由原点出发,裁刀依次遍游每块样片中的某一个顶点(该顶点为裁剪起始点,所在样片的其他顶点无需再游历)并返回原点,且在样片间移动轨迹无重复的最短路径,如图1所示的虚线路径.

图1 裁剪空行程路径的GTSP模型
假设有n块样片,且有n个裁剪起始点,并令样片编号与其裁剪起始点编号对应(编号0为原点).若第i块样片的裁剪起始点i与第j块样片的裁剪起始点j之间的空行程距离为di,j,则存在如下关系:
(2)
裁剪空行程的优化模型(目标函数)为:
(3)
根据实际裁剪工艺要求,约束条件主要考虑裁刀和样片顶点集两大约束,具体包括:裁刀的起始点和终止点都是裁床的原点;裁刀到达和离开每块样片有且只有一次;裁刀在各样片之间的移动轨迹不重复(无子回路).定义样片外轮廓上的各线段的起点和终点为顶点(如图1中线段vi,1vi,2,对应顶点为vi,1和vi,2);定义样片外轮廓上的各弧线的起点和终点为顶点(如vi,1和vi,V(i)),若弧线角度大于90°时可每隔90°定义一个顶点.
2 裁剪路径优化算法
由图1可知,裁刀空行程的路径距离主要由样片裁剪起始点和裁剪顺序决定,因此可将其视为是一个NP优化问题.该优化问题的求解难度随样片数量的增加呈指数增大.为降低求解难度,本文采取分类优化的思路,即:①引入坐标中心点概念[9],依据最近规则选取各样片的裁剪起始点,即将GTSP问题转化为TSP问题,以此降低问题的求解难度;②利用改进蚁群算法优化样片裁剪顺序(即裁剪起始点游历顺序),以此生成空行程的最短路径.
2.1 裁剪起始点的确定
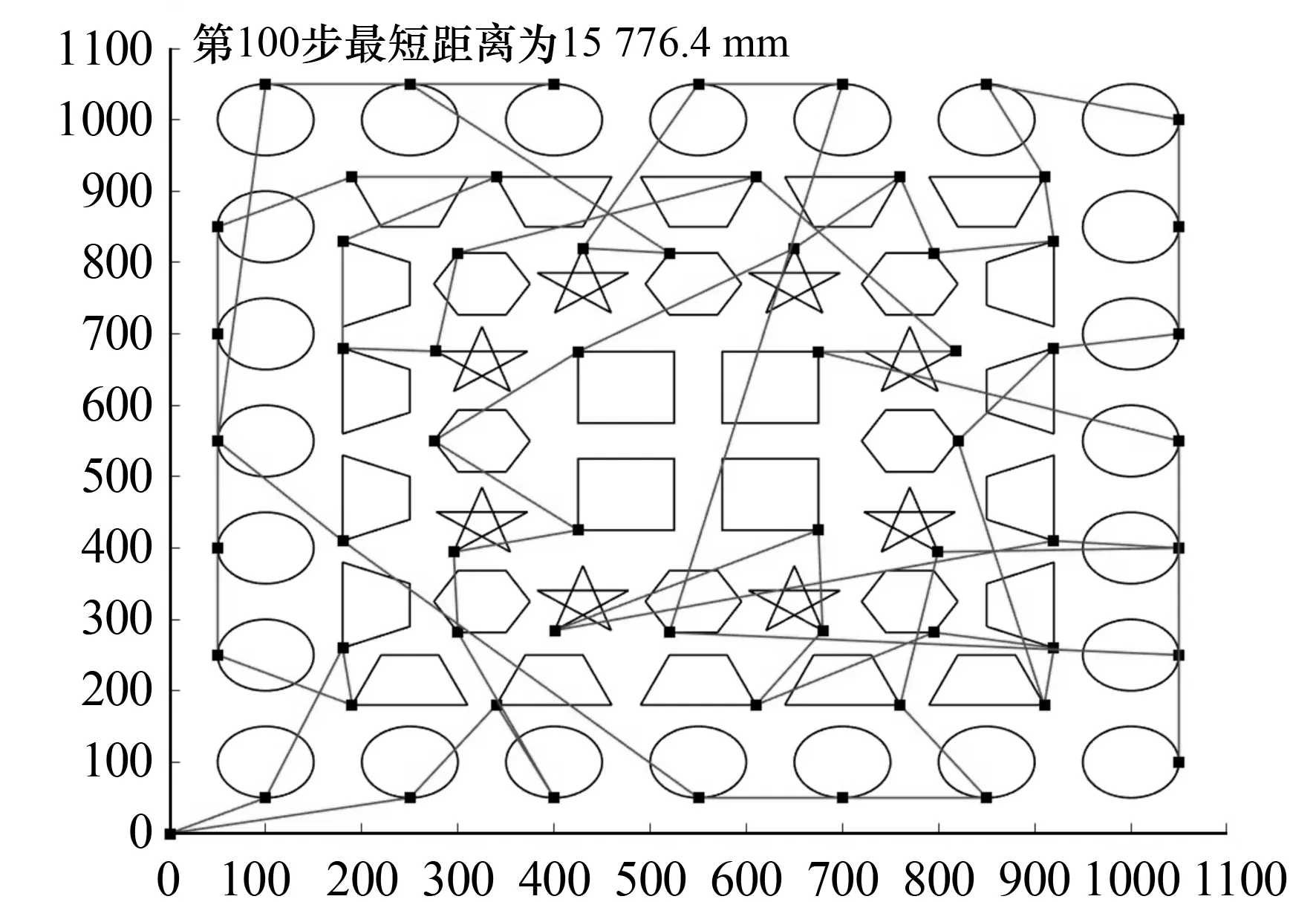
假设有n块样片,第i块样片有v(i)个顶点,第i块样片的第j个顶点vi,j(1 (4) 以坐标中心点C为参考点,定义第i个样片的第j个顶点与坐标中心点C之间的距离为di j c.di j c的计算公式为: (5) 根据式(5)即可求出所有的样片顶点与坐标中心点C的距离.从每块样片的顶点集合中选取一个距离C点最近的顶点vi,j,令其为所在样片的裁剪起始点.以此类推,最终获得所有样片的裁剪起始点集合,由此即可完成由GTSP向TSP的转化. 蚁群算法是一种求解TSP问题的经典算法[10],但传统蚁群算法自适应性差,容易陷入局部最优解和出现早熟现象,因此本文选用改进最大最小蚁群算法对已获得裁剪起始点的游历顺序进行优化排序. 1)路径的选择概率规则.假设有m只蚂蚁,τi j(0)和τi j(t)分别为样片i和样片j之间路径的信息素浓度初值和当前值,τi j(0)=C(C为常数).t时刻时,蚂蚁k根据路径上的信息素浓度强弱选择是否从样片i移动到样片j,其选择概率规则为: (6) 式(6)中:ηi j(ηi j=1/di j)为样片i和样片j之间路径的能见度,路径距离越短,能见度越高,选中几率越大;α为信息素因子,用以表征信息素浓度对蚂蚁移动的影响度;β为启发因子,用以表征信息素浓度与路径距离的相关性. 2)信息素自适应更新规则.t时刻时,任一路径上的信息素浓度都存在叠加或挥发现象,即信息素浓度是动态变化的.本文在传统蚁群算法的基础上对优质路径进行更新,并加入自适应更新功能.其具体方法为:每次迭代结束后,对所有蚂蚁移动的路径距离进行排序,并定义排序靠前的l只蚂蚁为精英蚂蚁;只对精英蚂蚁行走过的优质路径进行信息素更新,其更新规则[11]为: (7) (8) 式(8)中,μ的范围为[0.1~0.8].在该范围内信息素浓度可自适应地进行动态调整,而超出该范围则算法不更新或完全更新信息素浓度,以此避免算法出现早熟现象. 为了防止优质路径上的信息素因叠加或挥发过快而造成局部最优,需对路径上的信息素浓度进行限制.限制的方法为:①只允许优质路径才能增加信息素;②设置信息素浓度上、下限值.当更新后的信息素浓度在[τmin,τmax]范围内时,信息素浓度为更新值;当信息素浓度超过上限值或下限值时,信息素浓度为τmax或τmin,以此确保信息素浓度不超出有效范围.τmin和τmax的计算公式为: (9) 式(9)中,n为裁剪起始点的个数,0.05为蚂蚁构造最佳路径的可能性. 采用分类优化算法求解皮革裁剪空行程路径的具体步骤如下: step 1 初始化参数. step 2 按照式(4)计算坐标中心点C的x值与y值. step 3 按照式(5)计算各样片与坐标中心点的最近顶点,并令其为所在样片的裁剪起始点,从而获得所有样片的裁剪起始点集合. step 4 初始化蚁群算法的基本参数,让m只蚂蚁由原点出发,并令τi j(0)=τmax. step 6 判断蚂蚁k是否已遍游所有样片,若未完成则跳转至step 5,若完成则向下执行. step 7 判断所有蚂蚁是否都已构建完路径.若未完成则令k=k+1,并跳转step 5;若完成,则向下执行. step 8 按照式(7)、式(8)和式(9)更新优质路径信息素浓度. step 9 判断算法迭代次数是否达到上限Ncmax,若未达到,则清空禁忌表,同时令Nc=Nc+1,并跳转至步骤step 5;否则结束算法,输出裁刀空行程的最优路径. 选取一块面积为1 100 mm×1 100 mm的皮革为例进行实验.该皮革共包含62块待裁样片,样片编号如图2所示.将图2中的V25,1为第25块样片的第1个顶点,其余顶点按顺时针排序.形状相同的样片其顶点定义方法相同.按照数控裁剪机自带的裁剪算法获得的空行程裁剪路径如图3所示,其裁刀空行程路径的距离为15 776.4 mm.利用本文给出的算法获得的空行程裁剪路径如图4(a)所示,其空行程路径的距离为10 338.9 mm. 图2 待裁样片的布局图 图3 优化前的空行程路径 由图4(a)可知,应用本文提出的算法优化后的裁刀空行程路径为:V0,0→V19,1→V38,4→V54,2→V56,3→V60,4→V48,5→V30,3→V51,1→V33,4→V34,3→V14,1→V15,4→V35,3→V36,5→V37,4→V55,2→V39,3→V40,3→V22,2→V41,4→V58,4→V57,3→V59,3→V61,2→V62,1→V53,2→V52,2→V50,1→V49,6→V32,4→V31,4→V10,4→V11,4→V12,4→V13,4→V9,4→V47,5→V29,4→V8,4→V6,3→V7,4→V5,3→V28,4→V46,5→V4,3→V3,3→V26,3→V44,4→V45,4→V43,4→V42,4→V23,2→V24,2→V1,3→V2,3→V25,3→V27,4→V16,1→V17,1→V21,2→V20,2→V18,1→V0,0.该路径距离比优化前的空行程路径距离减少了5 437.5 mm,即缩短了34.5%的长度,且算法收敛性良好(见图4(b)). 图4 优化后的空行程路径效果 本文针对皮革裁剪过程中存在大量无效空行程的问题,运用分类优化算法对裁剪空行程路径模型进行了求解,结果表明优化后的空行程路径距离比优化前的空行程距离缩短了34.5%,实现了提高数控裁床加工效率的目的.本文在研究中未使用排料软件进行智能排料,故在原料的使用上存在一定的浪费;今后我们将进一步研究智能排料在本文算法中的应用,以此提高本文算法的适用性.2.2 裁剪顺序的确定


2.3 分类优化算法的求解步骤
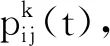
3 实验与分析


4 结论
